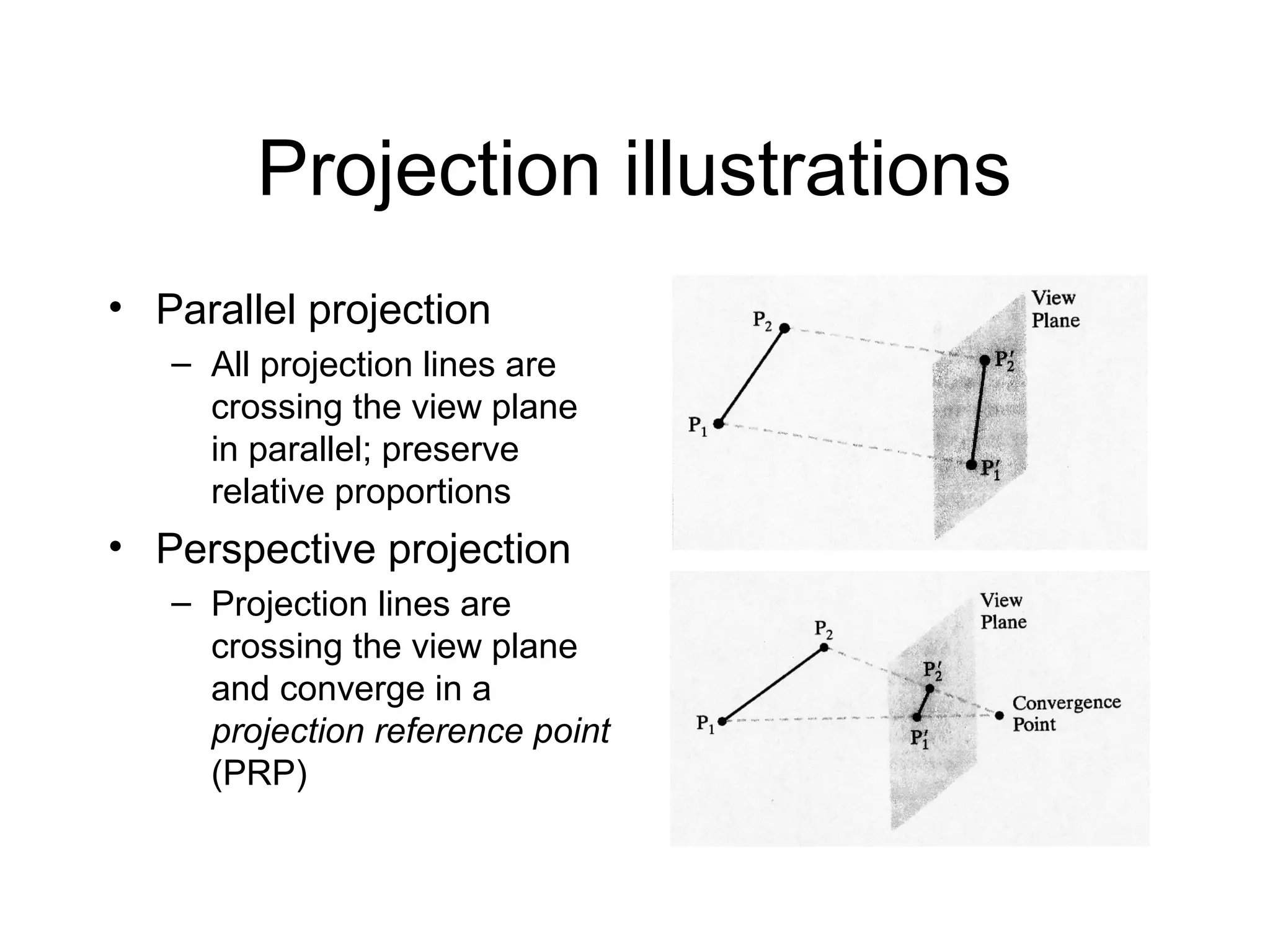
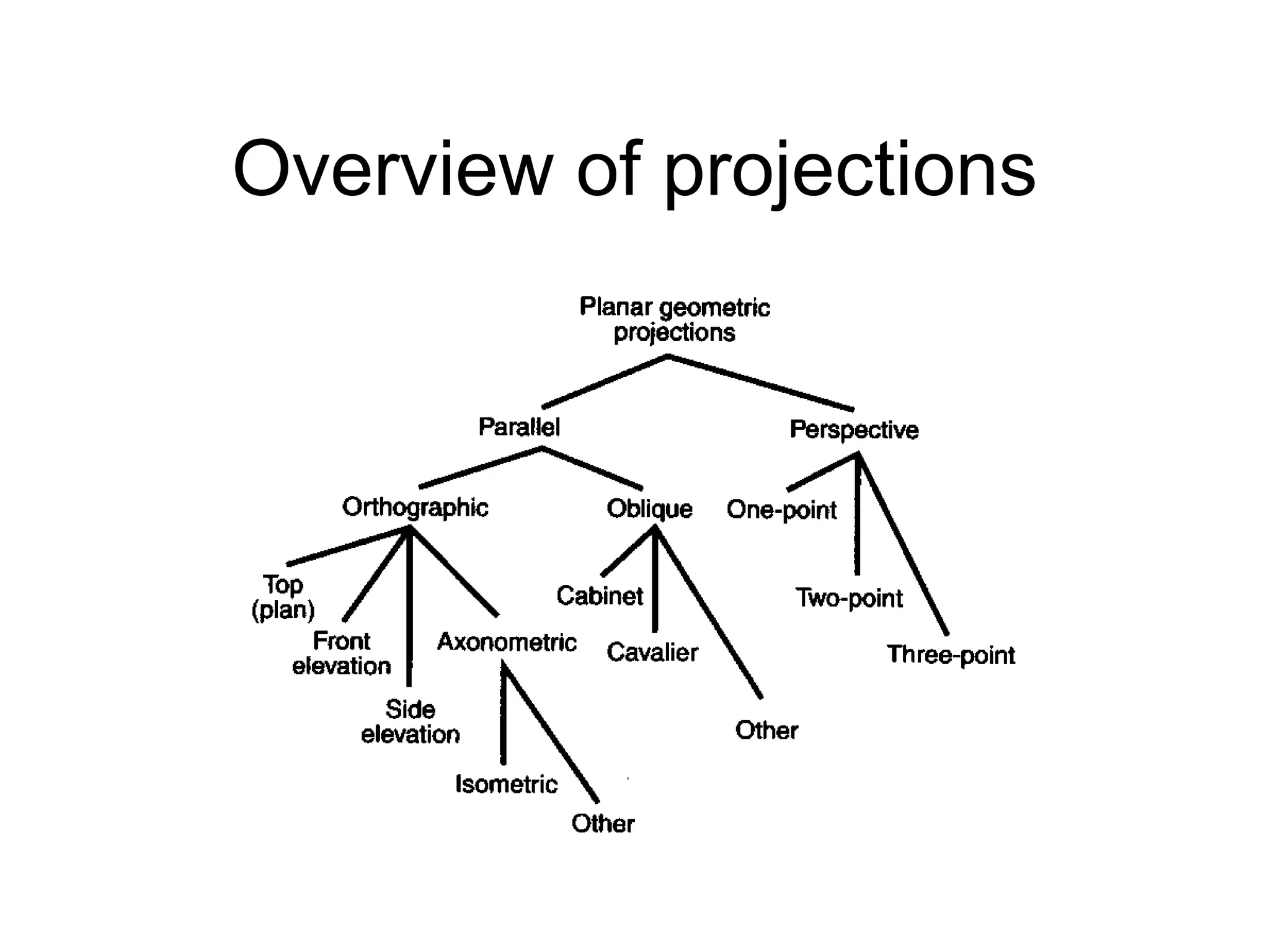
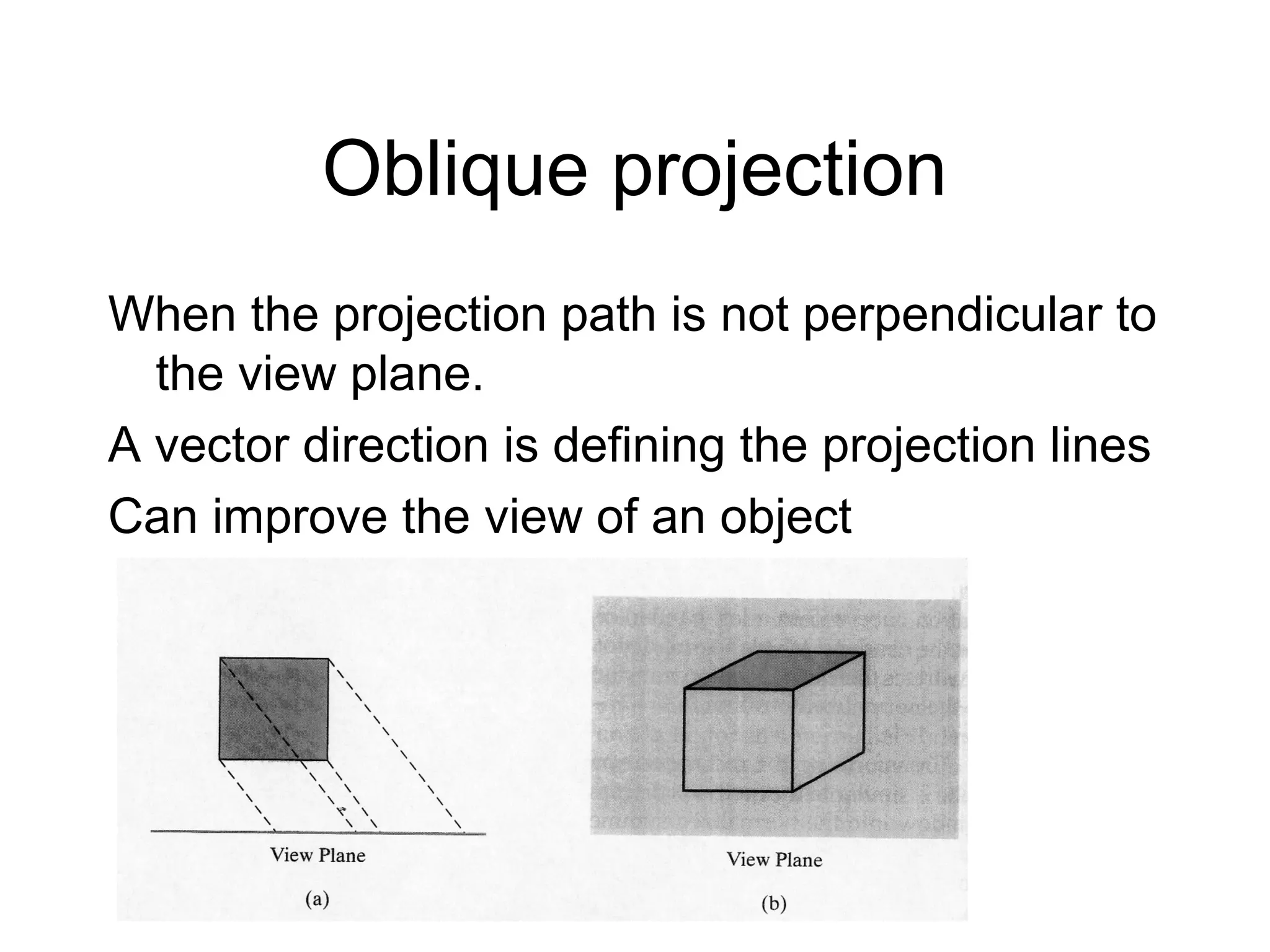
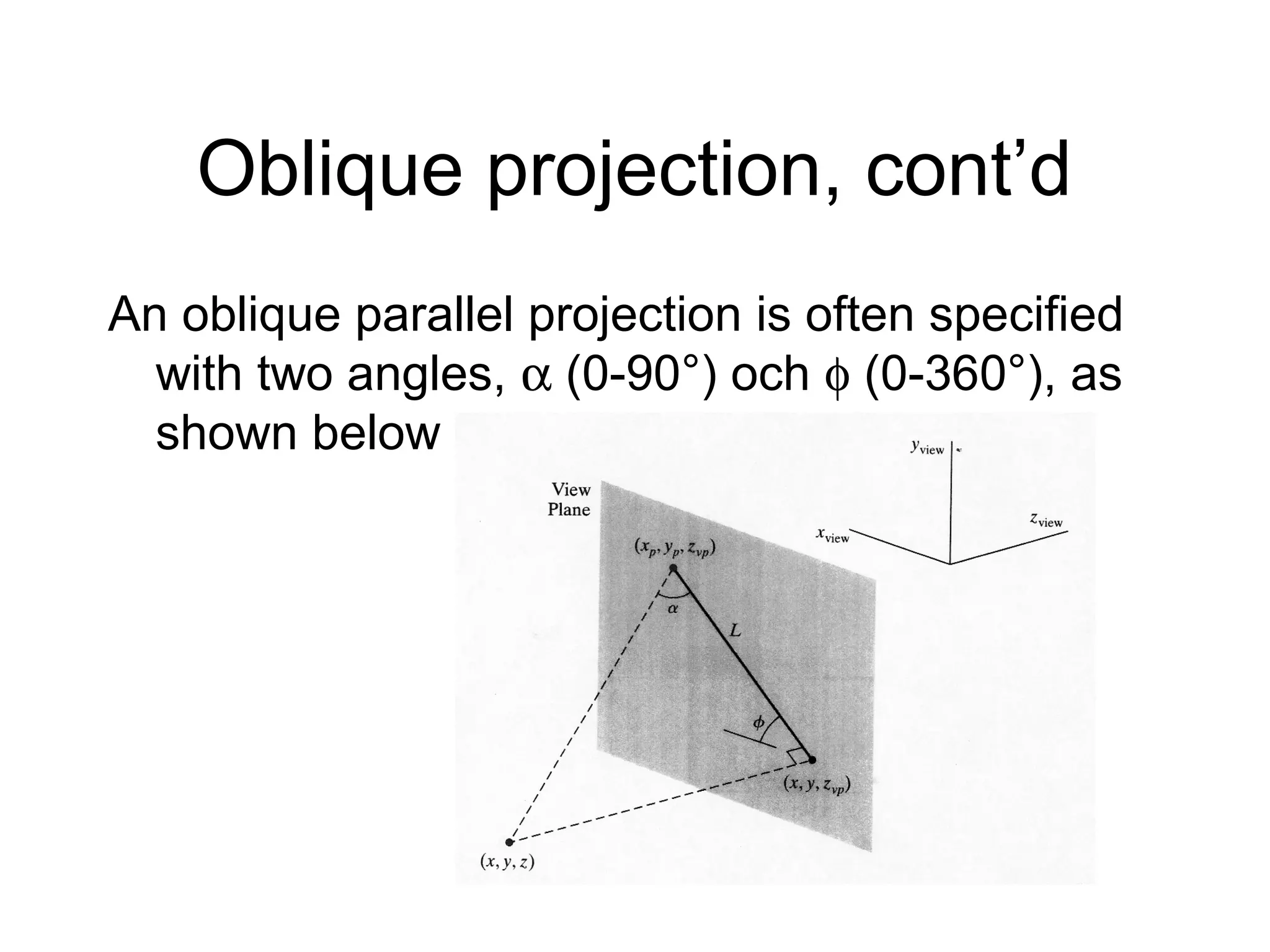
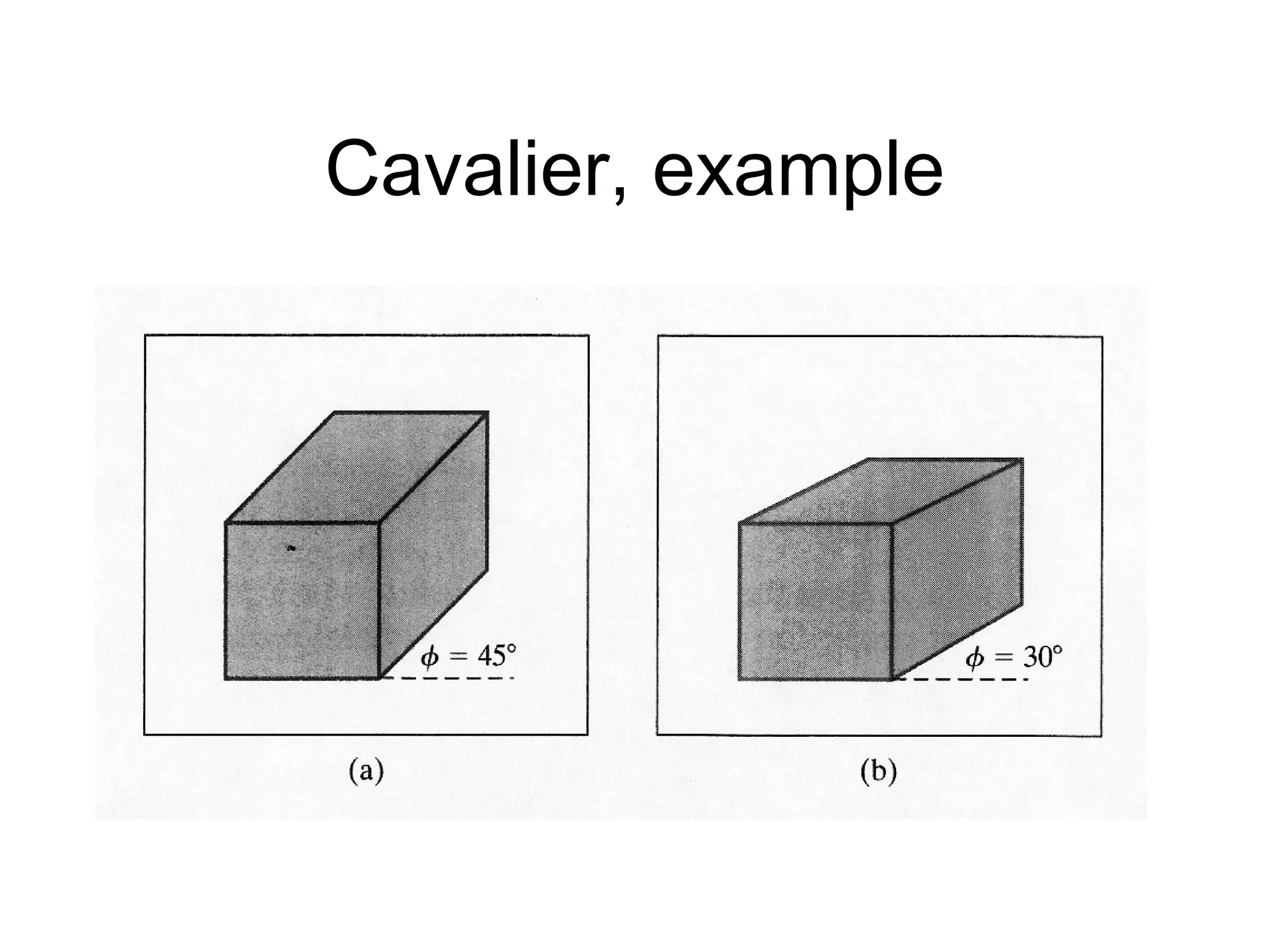
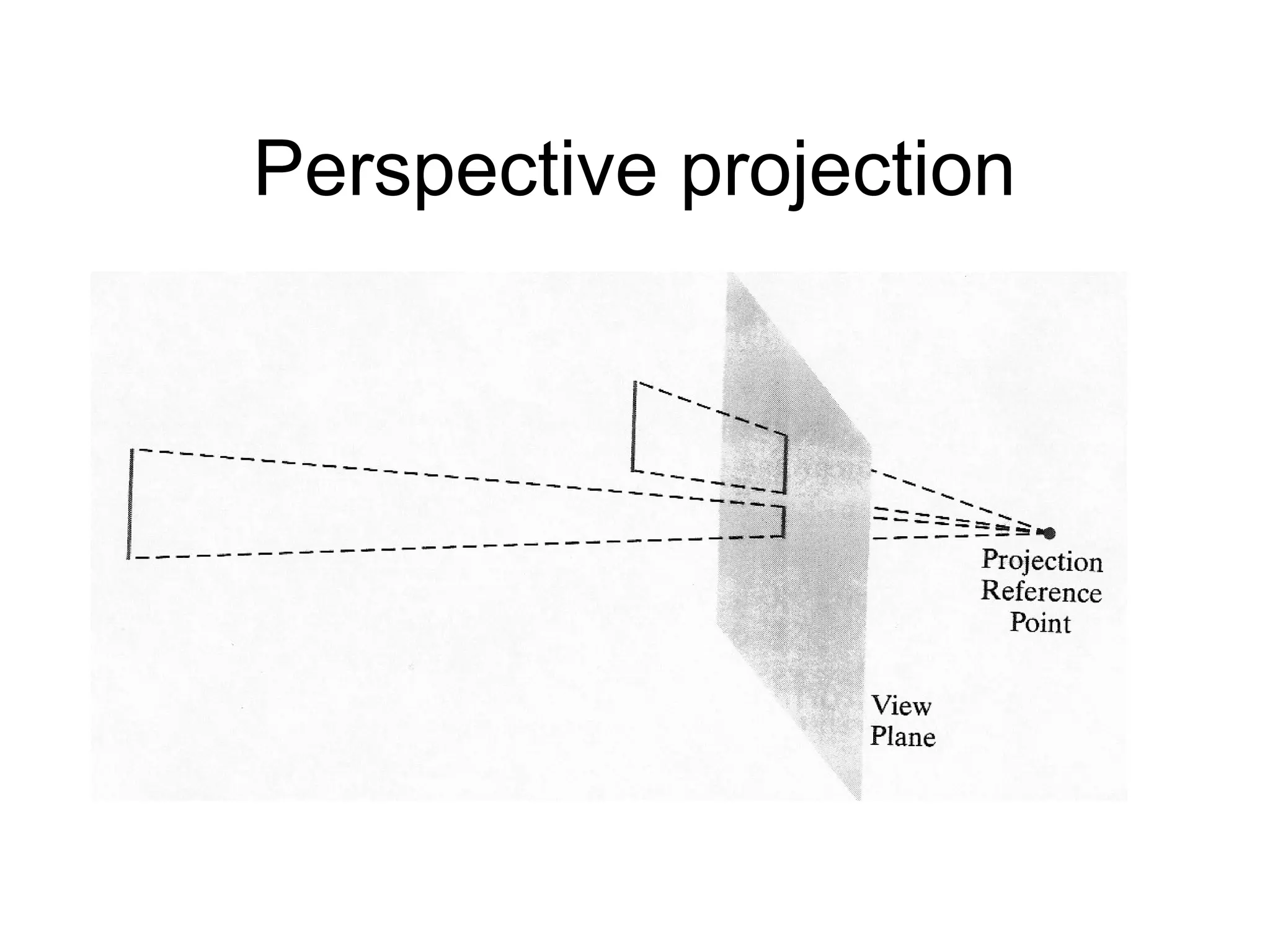
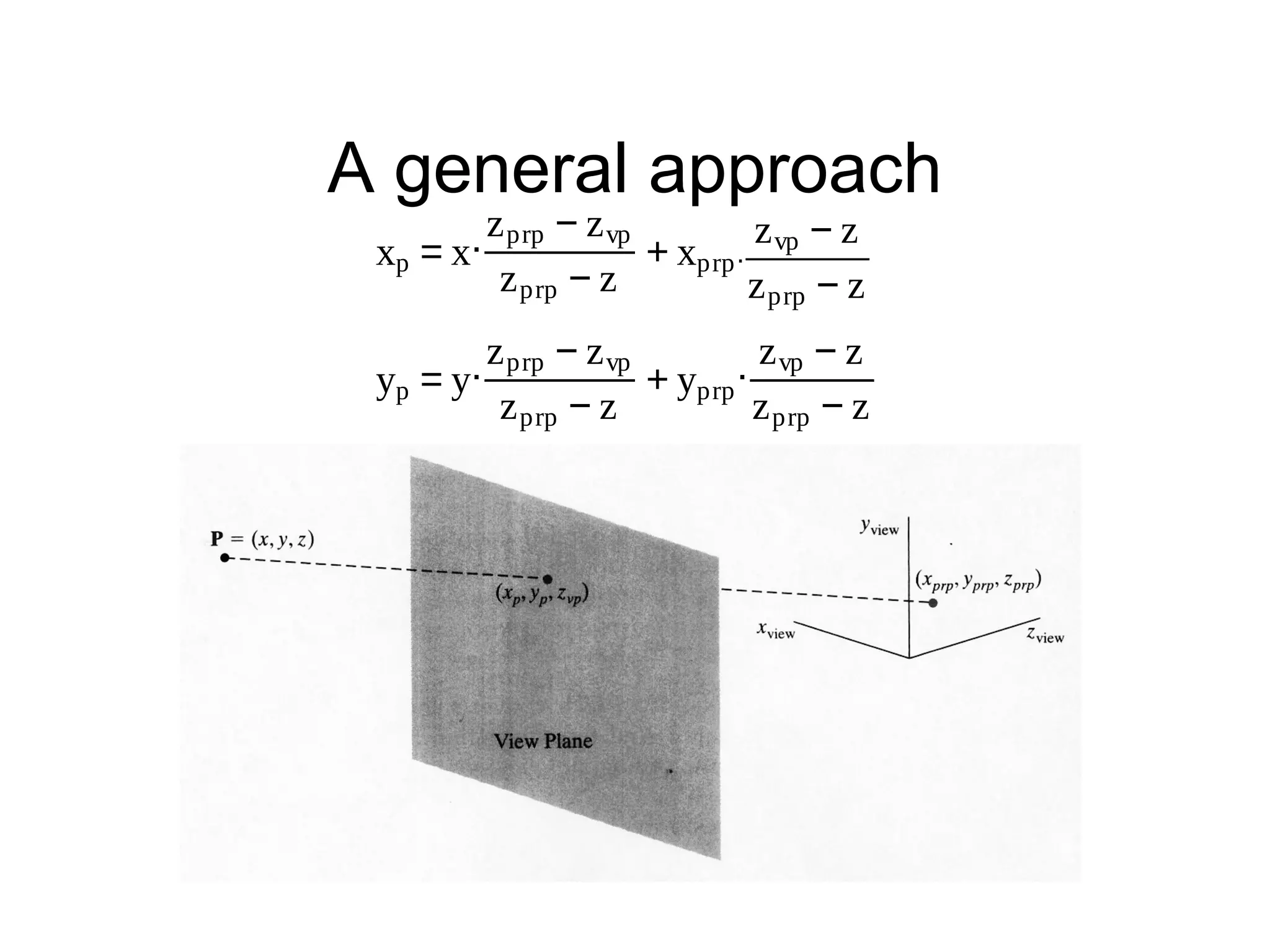
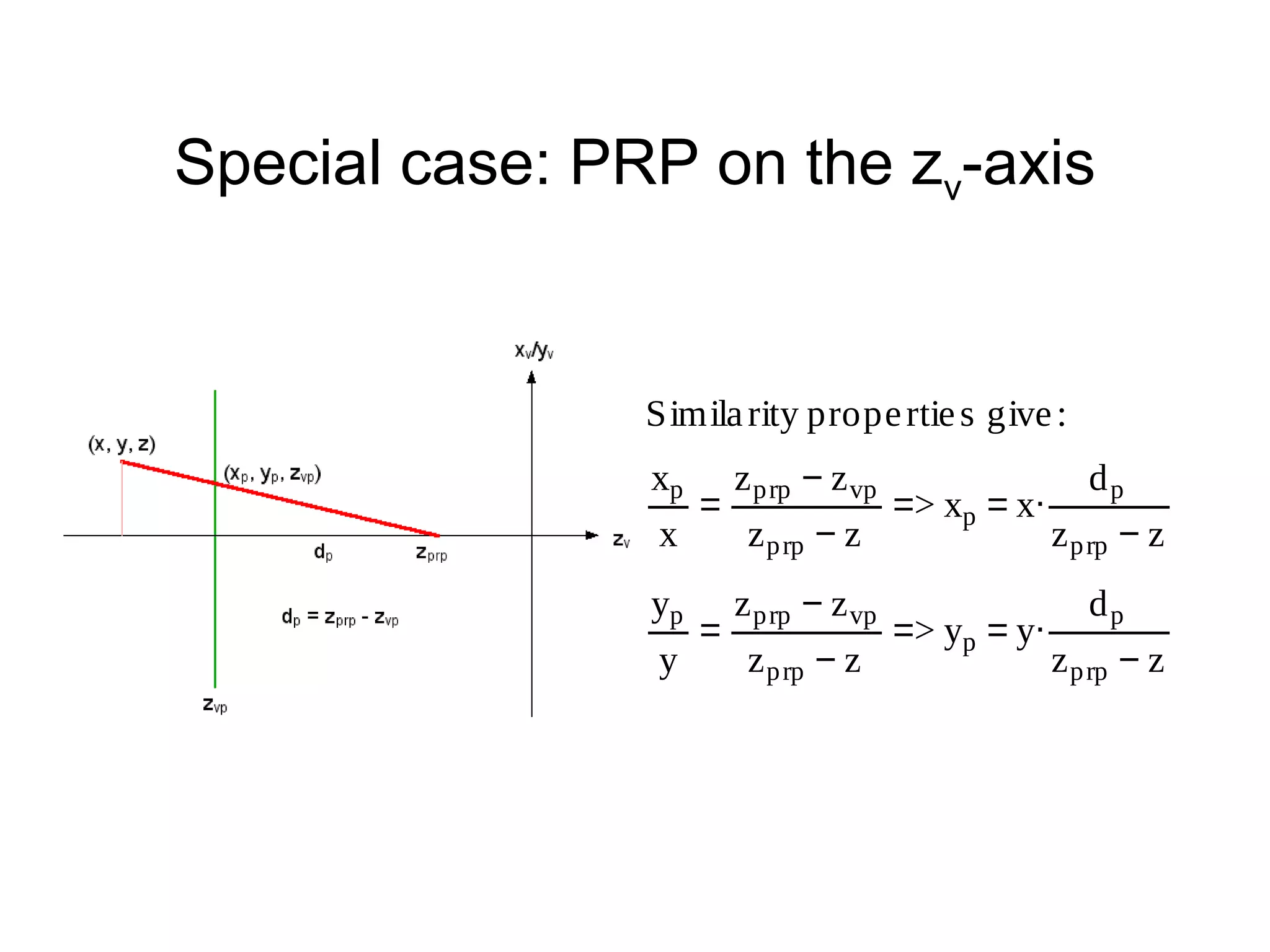
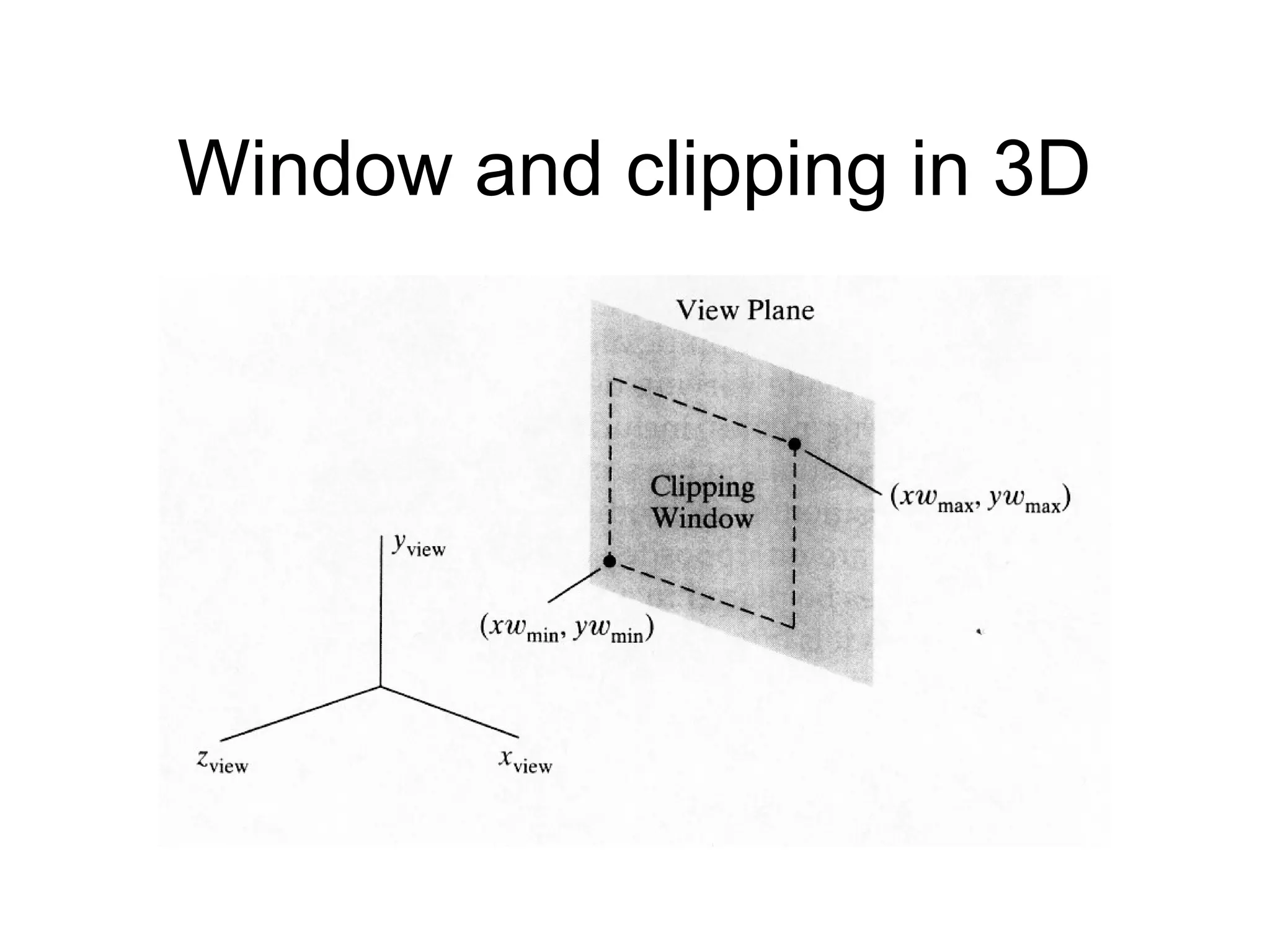
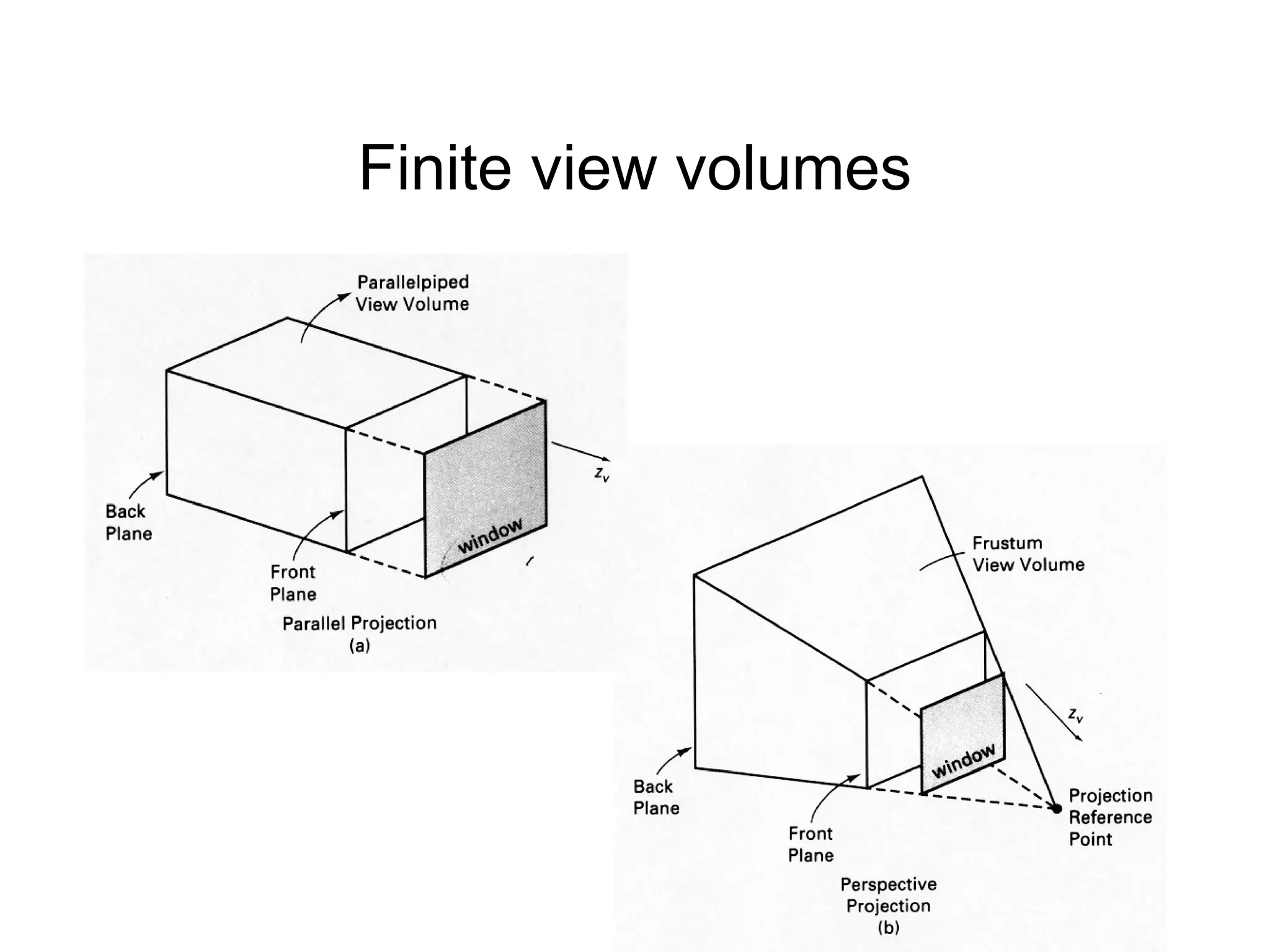
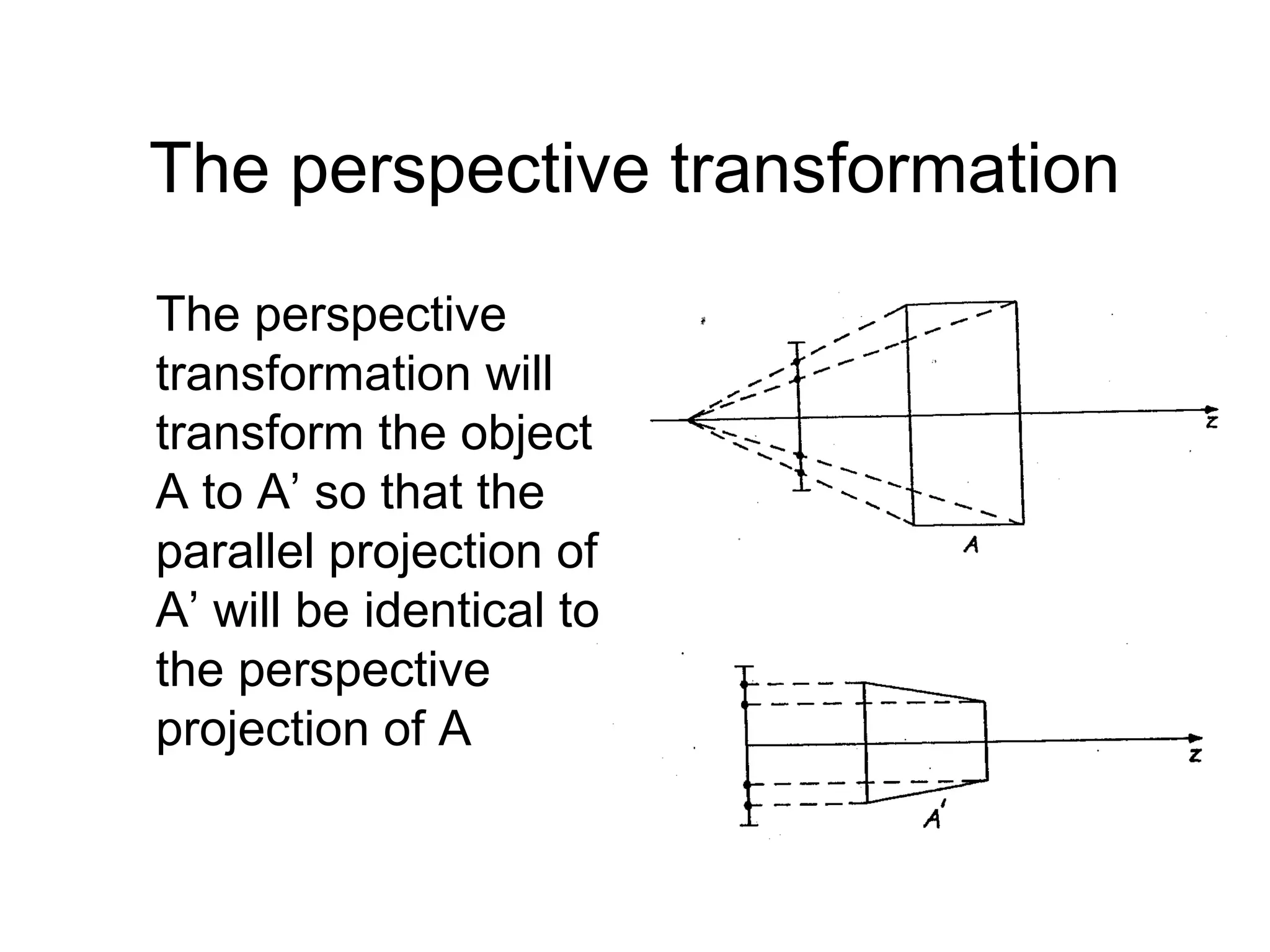
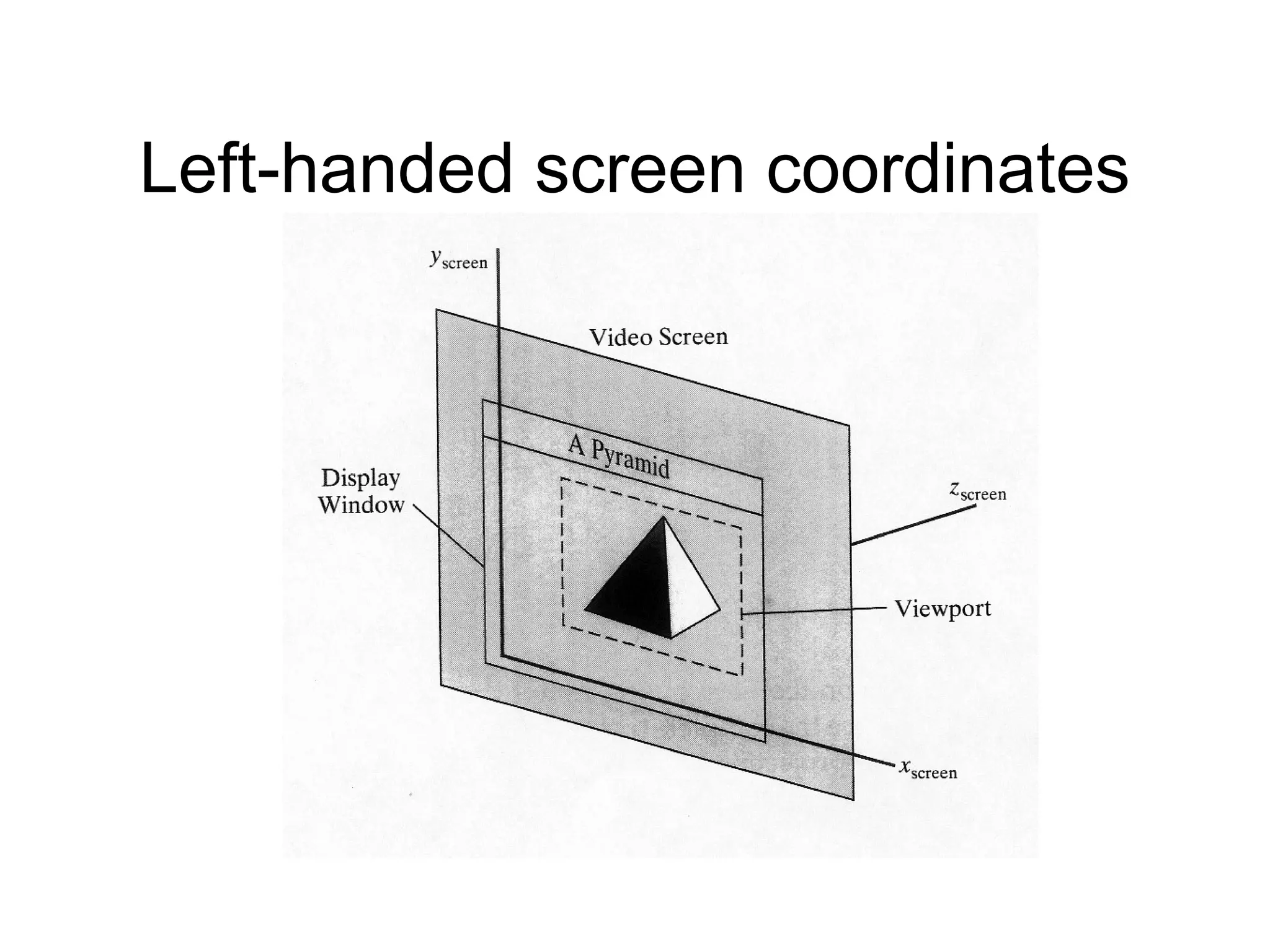
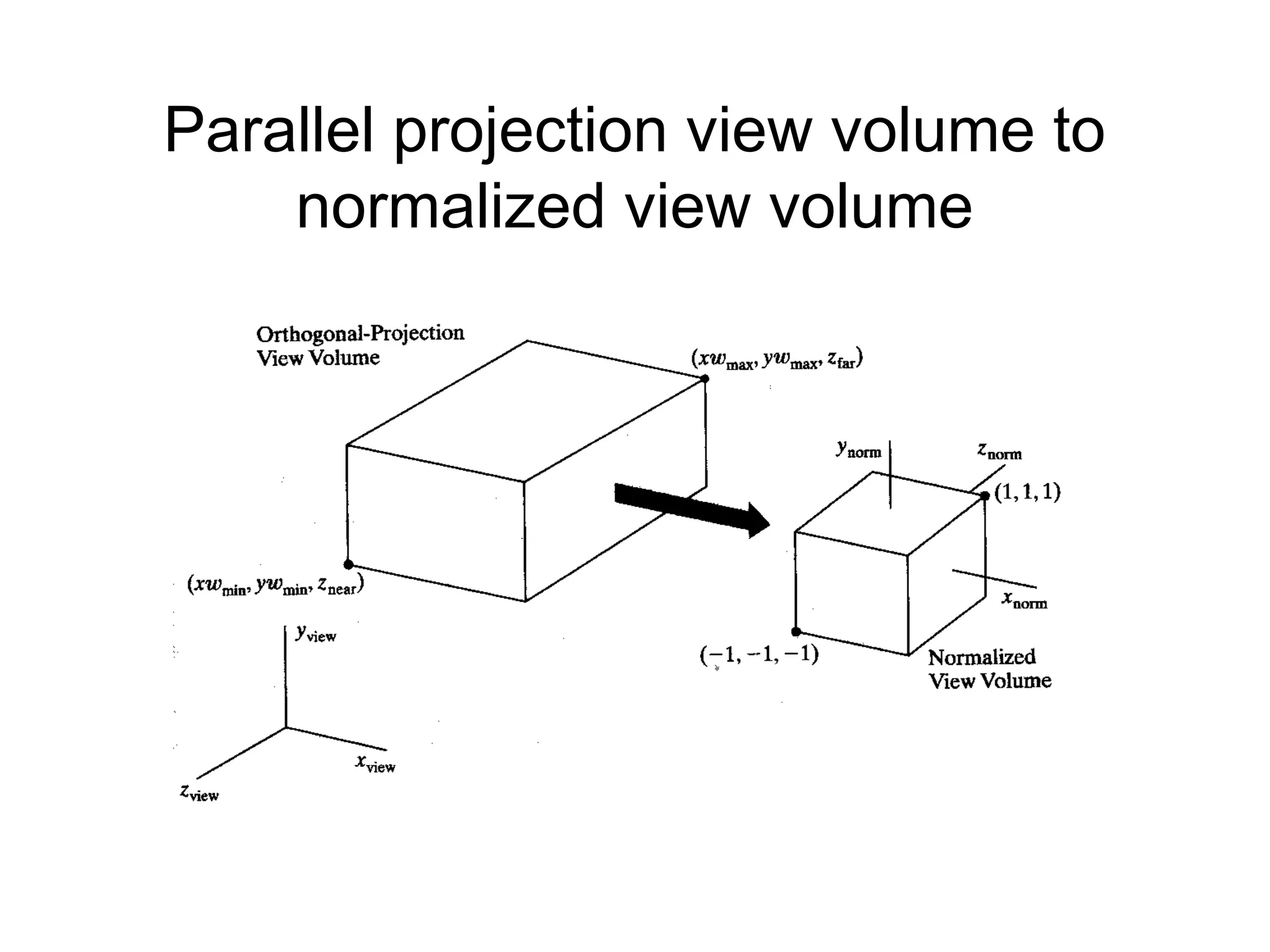
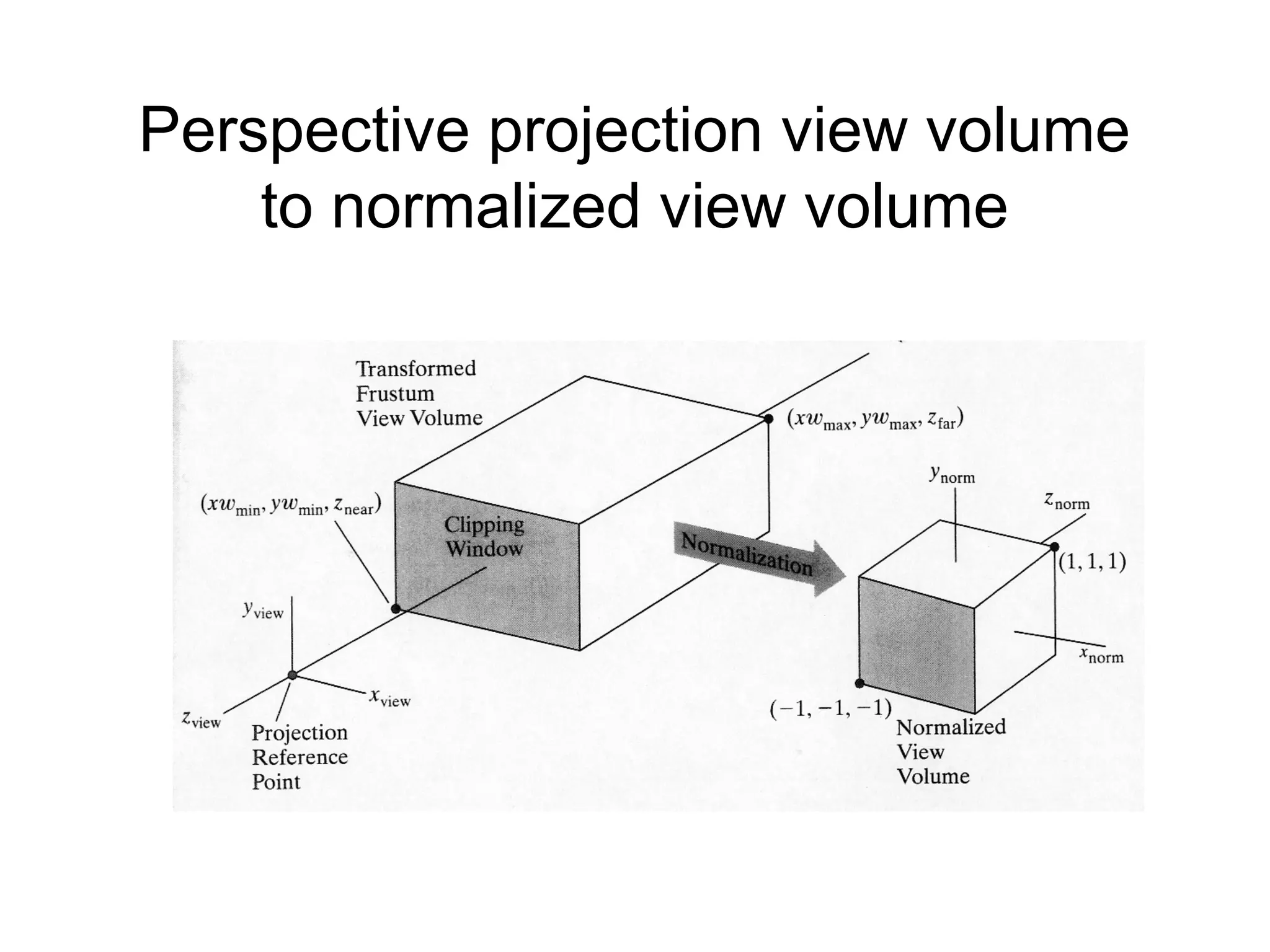
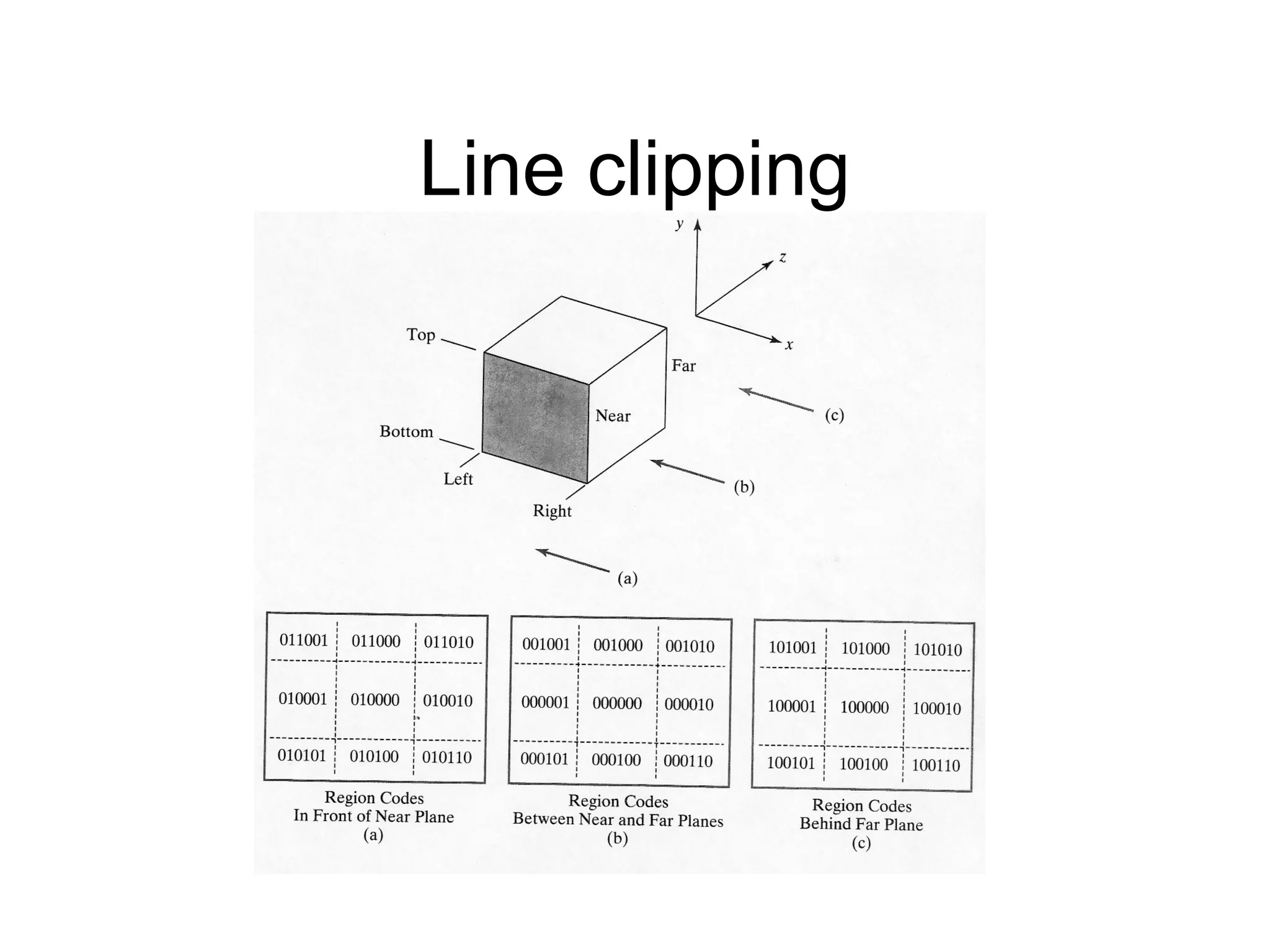
This document discusses 3D projections and clipping. It begins by describing parallel and perspective projections. It then covers various types of parallel projections like orthographic, oblique, cavalier and cabinet projections. Next it explains perspective projections and different approaches. The document also discusses window and clipping in 3D, including view volumes, finite view volumes, and 3D clipping algorithms. It provides details on clipping lines, polygons and examples. Finally it outlines the remaining tasks in the viewing pipeline after clipping.

1. Projections and clipping in 3D

2. Viewing and projection
Objects in WC are projected on to the
view plane, which is defined
perpendicular to the viewing direction
along the zv-axis. The two main types of
projection in Computer Graphics are:
• parallel projection
• perspective projection

3. Projection illustrations
• Parallel projection
– All projection lines are
crossing the view plane
in parallel; preserve
relative proportions
• Perspective projection
– Projection lines are
crossing the view plane
and converge in a
projection reference point
(PRP)

4. Overview of projections

5. Parallel projection
Two different types are used:
• Orthographic (axonometric,isometric)
– most common
– projection perpendicular to view plane
• Oblique (cabinet and cavalier)
– projection not perpendicular to view plane
– less common

6. Orthographic projection
Assume view plane at zvp (perpendicular to the zv-axis)
and (xv,yv,zv) an arbitrary point in VC
Then xp = xv
yp = yv
zp = zvp (zv is kept for depth purposes only)

7. Oblique projection
When the projection path is not perpendicular to
the view plane.
A vector direction is defining the projection lines
Can improve the view of an object

8. Oblique projection, cont’d
An oblique parallel projection is often specified
with two angles, α (0-90°) och φ (0-360°), as
shown below

9. Oblique formula (from fig.)
Assume (x,y,z) any point in VC (cp. xv,yv,zv)
cos φ=(xp-x)/L => xp=x+L.cos φ
sin φ =(yp-y)/L => yp=y+L. sin φ
Also tan α=(zvp-z)/L, thus L=(zvp-z)/tan α= =L1(zvpz), where L1=cot α
Hence
xp = x + L1(zvp - z).cos φ
yp = y + L1(zvp - z).sin φ
Observe: if orthographic projection, then L 1=0

10. Cavalier and Cabinet
When
• tan α = 1 then the projection is called
Cavalier (α = 45°)
• tan α = 2 then the projection is called
Cabinet (α ≈ 63°)
φ usually takes the value 30° or 45°

11. Cavalier, example

12. Perspective projection

13. A general approach
. z prp − z vp + xprp . z vp − z
xp = x
z prp − z
z prp − z
. z prp − z vp + y . z vp − z
yp = y
prp
z prp − z
z prp − z

14. Special cases
Various restrictions are often used, such as:
• PRP on the zv-axis (used in the next
approach) => xprp=yprp=0
• PRP in the VC origin => xprp=yprp=zprp=0
• view plane in the xvyv-plane => zvp=0
• view plane in the xvyv-plane and PRP on the
zv-axis =>xprp=yprp=zvp=0

15. Special case: PRP on the zv-axis
Simila rity prope rtie s give :
xp
x
yp
y
=
=
z prp − z vp
z p rp − z
z prp − z vp
z p rp − z
=> xp = x.
=> yp = y.
dp
z p rp − z
dp
z p rp − z

16. Window and clipping in 3D

17. Window in 3D => View Volume
A rectangular window on the view plane
corresponds to a view volume of type:
• infinite parallelepiped (parallel
projection)
• ”half-infinite” pyramid with apex at PRP
(perspective projection)

18. View volumes

19. Finite view volumes
To get a finite volume (one or) two extra
zv-boundary planes, parallel to the view
plane, are added: the front (near) plane
and the back (far) plane resulting in:
• a rectangular parallelepiped (parallel
projection)
• a pyramidal frustum (perspective
projection)

20. Finite view volumes

21. ”Camera” properties
The two new planes are mainly used as far and
near clipping planes to eliminate objects
close to and far from PRP (cp. the camera)
Other camera similarities:
• PRP close to the view plane => ”wide angle”
lens
• PRP far from the view plane => ”tele photo”
lens
Matrix representations for both parallel and perspective projections are possible (see text
book)

22. 3D Clipping
A 3D algorithm for clipping identifies and
saves those surface parts that are
within the view volume
Extended 2D algorithms are well suited
also in 3D; instead of clipping against
straight boundary edges, clipping in 3D
is against boundary planes, i.e. testing
lines/surfaces against plane equations

23. Clipping planes
Testing a point against the front and back
clipping planes are easy; only the zcoordinate has to be checked
Testing against the other view volume sides are
more complex when perspective projection
(pyramid), but still easy when parallel
projection, since the clipping sides are then
parallel to the x- and y-axes

24. Clipping when perspective projection
Before clipping, convert the view volume, a
pyramidal frustum, to a rectangular
parallelepiped (see next figure)
Clipping can then be performed as in the case
of parallel projection, which means much less
processing
From now on, all view volumes are assumed to
be rectangular parallelepipeds (either
including the special transformation or not)

25. The perspective transformation
The perspective
transformation will
transform the object
A to A’ so that the
parallel projection of
A’ will be identical to
the perspective
projection of A

26. Normalized coordinates
A possible (and usual!) further transformation is
to a unit cube; a normalized coordinate
system (NC) is then introduced, with either
0≤x,y,z≤1 or -1≤x,y,z≤1
Since screen coordinates are often specified in
a left-handed reference system, also
normalized coordinates are often specified in
a left-handed system, which means, for
instance, viewing in the positive z-direction

27. Left-handed screen coordinates

28. Parallel projection view volume to
normalized view volume

29. Perspective projection view volume
to normalized view volume

30. Advantages with the
parallelepiped/unit cube
• all view volumes have a standard shape
and corresponds to common output
devices
• simplified and standardized clipping
• depth determinations are simplified
when it comes to Visible Surface
Detection

31. Clipping in more detail
Both the 2D algorithms, Cohen-Sutherland’s for
line clipping and Sutherland-Hodgeman’s for
polygon clipping, can easily be modified to 3D
clipping.
One of the main differences is that clipping has
to be performed against boundary planes
instead of boundary edges
Another is that clipping in 3D generally needs to
be done in homogeneous coordinates

32. Clipping details,cont’d
With matrix representation of the viewing and projection
transformations, the matrix M below represent the
concatenation of all various transformations from
world coordinates to normalized, homogeneous
projection coordinates with h taking any real value!
⎛xh ⎞
⎛x ⎞
⎜y ⎟
h
.⎜y ⎟
⎜ ⎟=M ⎜ ⎟
⎜z ⎟
⎜z h ⎟
⎝1 ⎠
⎝h ⎠

33. Line clipping

34. Polygon clipping
Graphics packages typically deal only with
objects made up by polygons
Clipping an object is then broken down in
clipping polygon surfaces
First, some bounding surface is tested
Then, vertex lists as in 2D but now processed
by 6 clippers!
Additional surfaces need to ”close” cut objects
along the view volume boundary
Concave objects are often split

35. Example, object clipping

36. Viewing pipeline
After the clipping routines have been
applied to the normalized view volume,
the remaining tasks are:
• Visibility determination
• Surface rendering
• Transformation to the viewport (device)