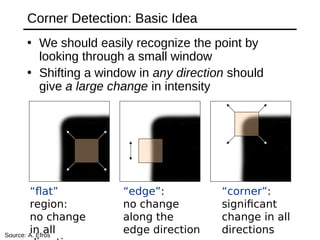
Here are the key steps in Harris corner detection: 1. Compute the autocorrelation matrix M for a window around each pixel using: M = ∑w(x,y)[IxIx IxIy] [IxIy IyIy] Where Ix and Iy are the gradients of the image I in x and y directions. 2. Compute the corner response function R = det(M) - k(trace(M))^2 3. A large R value indicates a corner. Threshold R to find candidate corner points. 4. Refine the candidate locations using interpolation. So in summary, Harris detection looks for pixels with

1. 1
of
64

2. 2
of
65
3-D Coordinate Spaces
Remember what we mean by a 3-D
coordinate space
x axis
y axis
z axis
P
y
z
x
Right-Hand
Reference System

3. 3
of
65

4. 4
of
65
Position of camera in space

5. 5
of
65
The Up And Look Vectors
Up vector
Look vector
Position
Projection of up
vector
The look vector : indicates the direction in which the camera is
pointing
The up vector : determines how the camera is rotated

6. 6
of
65
Rotations In 3-D
When we performed rotations in two
dimensions we only had the choice of
rotating about the z axis
In the case of three dimensions we have
more options
– Rotate about x – pitch
– Rotate about y – yaw
– Rotate about z - roll

7. 7
of
64
Simple pinhole camera
A pinhole camera is a simple camera without a lens and with a single
small aperture. Light rays pass through the aperture and project an
inverted image on the opposite side of the camera. Think of the virtual
image plane as being in front of the camera and containing the upright
image of the scene.

8. 8
of
65

9. 9
of
65
-intrinsics,
-extrinsics,
-distortion coefficients.
Camera parameters include

10. 10
of
65
Intrinsic Parameters
• principal point (u0,v0)
• scale factors (dx,dy)
• aspect ratio distortion factor 
• focal length f
• lens distortion factor 
(models radial lens distortion)
C
(u0,v0)
f
•intrinsic parameters are of the camera
device

11. 11
of
65
Extrinsic Parameters
• translation parameters
t = [tx ty tz]
• rotation matrix
r11 r12 r13 0
r21 r22 r23 0
r31 r32 r33 0
0 0 0 1
R = Are there really
nine parameters?
extrinsic parameters are where the camera sits in the world

12. 12
of
65
What Is Camera Calibration?
Geometric camera calibration
is the process of estimating intrinsic and/or extrinsic
parameters
You can use these parameters to
- correct for lens distortion,
- measure the size of an object in world units,
- determine the location of the camera in the
scene.

13. 13
of
65
Camera Calibration Examples

14. 14
of
65

15. 15
of
65
The camera matrix does not account for lens
distortion because an ideal pinhole camera does
The Computer Vision Toolbox™ calibration
algorithm uses the camera model proposed by
Jean-Yves Bouguet

16. 16
of
65
Scaling
• Scaling changes the size of an
object and involves two scale
factors, Sx and Sy for the x- and
y- coordinates respectively.
• Scales are about the origin.
• We can write the components:
p'x = sx • px
p'y = sy • py
or in matrix form:
P' = S • P
Scale matrix as:







y
x
s
s
S
0
0
P
P’

17. 17
of
65
Translation
A translation moves all points in
an object along the same straight-
line path to new positions.
The path is represented by a
vector, called the translation or
shift vector.
We can write the components:
p'x = px + tx
p'y = py + ty
or in matrix form:
P' = P + T
tx
ty
x’
y’
x
y
tx
ty
= +
(2, 2)
= 6
=4
?

18. 18
of
65
To estimate the camera parameters
You need to have 3-D world points and their
corresponding 2-D image points.
You can get these correspondences using multiple
images of a calibration pattern, such as a
checkerboard. Using the correspondences, you can
solve for the camera parameters.

19. 19
of
65
calibration pattern

20. 20
of
65
Chapter 14
Tut 14.1: Viewing Parameters
All viewing parameters
controlled by slider bars

21. 21
of
65
Calibration Application

22. 22
of
65
Calibration invers
After you calibrate a camera, to evaluate the
accuracy of the estimated parameters, you
can:
-Plot the relative locations of the camera and
the calibration pattern
-Calculate the re-projection errors.
-Calculate the parameter estimation errors.
-Use the Camera Calibrator to perform
camera calibration and evaluate the
accuracy of the estimated parameters.

23. 23
of
65
Calibration Application

24. 24
of
33
What Are Projections?
Our 3-D scenes are all specified in 3-D
world coordinates
To display these we need to generate a 2-D
image - project objects onto a picture
plane
So how do we figure out these projections?
Picture Plane
Objects in
World Space

25. 25
of
33
Converting From 3-D To 2-D
Projection is just one part of the process of
converting from 3-D world coordinates to a
2-D image
Clip against
view volume
Project onto
projection
plane
Transform to
2-D device
coordinates
3-D world
coordinate
output
primitives
2-D device
coordinates

26. 26
of
33
Types Of Projections
There are two broad classes of projection:
– Parallel: Typically used for architectural and
engineering drawings
– Perspective: Realistic looking and used in
computer graphics
Perspective ProjectionParallel Projection

27. 27
of
65
Parallel Projection

28. 28
of
65
Perspective Projection

29. 29
of
33
Types Of Projections (cont…)
For anyone who did engineering or technical
drawing

30. 30
of
33
Parallel Projections
Some examples of parallel projections
Orthographic Projection
Isometric Projection

31. 31
of
33
Isometric Projections
Isometric projections have been used in
computer games from the very early days
of the industry up to today
Q*Bert Sim City Virtual Magic Kingdom

32. 32
of
33
Perspective Projections
Perspective projections are much more
realistic than parallel projections

33. 33
of
33
Perspective Projections
There are a number of different kinds of
perspective views
The most common are one-point and two
point perspectives
One Point Perspective
Projection
Two-Point
Perspective
Projection

34. 34
of
65
Camera calibration revisited
What if world coordinates of reference 3D points are not
known?
We can use scene features such as vanishing points
Vanishing
point
Vanishing
line
Vanishing
point
Vertical vanishing
point
(at infinity)

35. 35
of
65
Camera calibration revisited

36. 36
of
65
1
2
3
4
5
5.3
2.8
3.3
Camera height
Measuring height

37. 37
of
65
Measuring height without a ruler

38. 38
of
65
Vanishing points
• All lines having the same direction share the same vanishing point
image plane
line in the scene
vanishing point v
camera
center

39. 39
of
65
Computing vanishing points
• X∞ is a point at infinity, v is its projection: v = PX∞
• The vanishing point depends only on line direction
• All lines having direction D intersect at X∞
















1
30
20
10
tdz
tdy
tdx
tX
















t
dtz
dty
dtx
/1
/
/
/
30
20
10













0
3
2
1
d
d
d
X
v
X0 Xt

40. 40
of
65
Calibration from vanishing points
Consider a scene with three orthogonal vanishing directions:
v2
v1
.
v3
.
ote: v1, v2 are finite vanishing points and v3 is an infinite vanishing point

41. 41
of
65
Calibration from vanishing points
Consider a scene with three orthogonal vanishing directions:
v2
v1
.
v3
.
We can align the world coordinate system with these direction

42. 42
of
65
Calibration from vanishing points
• p1 = P(1,0,0,0)T – the vanishing point in the x direction
• Similarly, p2 and p3 are the vanishing points in the y and z
directions
• p4 = P(0,0,0,1)T – projection of the origin of the world coordinate
system
• Problem: we can only know the four columns up to independent
scale factors, additional constraints needed to solve for them
 4321 ppppP 











****
****
****

43. 43
of
65
Can solve for focal length, principal pointCannot recover focal
length, principal point is
the third vanishing point

44. 1 2 3 4
1
2
3
4
Measurements on planes
Approach: unwarp then measure
What kind of warp is this?

45. Image rectification
To unwarp (rectify) an image
• solve for homography H given p and p′
– how many points are necessary to solve for H?
p
p′

46. 46
of
65

47. 47
of
65
Calibration from vanishing points:
Summary
• Solve for K (focal length, principal point) using three
orthogonal vanishing points
• Get rotation directly from vanishing points once calibration
matrix is known
• Advantages
• No need for calibration chart, 2D-3D correspondences
• Could be completely automatic
• Disadvantages
• Only applies to certain kinds of scenes
• Inaccuracies in computation of vanishing points
• Problems due to infinite vanishing points

48. 48
of
65
Introduction to 3D Imaging
There are several ways to calculate
depth information using 2D camera
sensors or other optical sensing
technologies.

49. 49
of
65

50. 50
of
65

51. 51
of
65
Human binocular vision

52. 52
of
65

53. 53
of
65
Double vision.
Vivek Nityananda, and Jenny C. A. Read J Exp Biol
2017;220:2502-2512
© 2017. Published by The Company of Biologists Ltd

54. 54
of
65
stereo camera
• Stereo vision is the process of extracting 3-D
information from multiple 2-D views of a scene
• A stereo camera is a type of camera with two or
more image sensors. This allows the camera to
simulate human binocular vision and therefore
gives it the ability to perceive depth.

55. 55
of
65
Two-view geometry
• In this case we have two camera views capture the
same scene from two different viewpoints
• from two images, we are interested in estimating the 3D
structure of the scene

56. 56
of
65
Two-view geometry
• b is the baseline, or
distance between the two
cameras
• f is the focal length of a
camera
• XA is the X-axis of a
camera
• ZA is the optical axis of a
camera
• P is a real-world point
defined by the coordinates
X, Y, and Z
• uL is the projection of the
real-world point P in an
image acquired by the left

57. 57
of
65
Two-view geometry
• Since the two cameras are separated by distance “b”, both
cameras view the same real-world point P in a different
location on the 2-dimensional images acquired.
The X-coordinates of points uL and uR are given by
uL = f * X/Z
and
uR = f * (X-b)/Z
Distance between those two projected points is known
as “disparity” and we can use the disparity value to
calculate depth information, which is the distance
between real-world point “P” and the stereo vision
system.
disparity = uL – uR = f *
b/z

58. 58
of
65
Disparity
• Disparity refers to difference in pixel position between
two camera images. Assuming left image in stereo vision
camera has a pixel at position (1, 30) and the same pixel
is present at position (4, 30) in right image, the disparity
value or difference is (4 – 1) =3. Disparity value is
inversely proportional to depth as per the above formula.

59. 59
of
65
Left image Right Image Right Image
Depth Image

60. 60
of
65
Stereo Vision
depth map

61. Interest Points and Corners
An interest point may be composed of various types of corner,
edge, and maxima shapes. In general, a good interest point must
be easy to find and ideally fast to compute; it is hoped that the
interest point is at a good location to compute a feature descriptor.
The interest point is thus the qualifier or keypoint around which a
feature may be described

62. Example: estimating “fundamental
matrix” that corresponds two
views
Slide from Silvio Savarese

63. Example: structure from motion

64. interest points
• Note: “interest points” =
“keypoints”, also sometimes called
“features”
• Many applications
– tracking: which points are good to
track?
– recognition: find patches likely to tell
us something about object category
– 3D reconstruction: find
correspondences across different views

65. This class: interest points
• Suppose you have
to click on some
point, go away
and come back
after I deform the
image, and click
on the same
points again.
– Which points
would you choose?
original
deformed

66. Overview of Keypoint Matching
K. Grauman, B. Leibe
Af Bf
B1
B2
B3A1
A2 A3
Tffd BA ),(
1. Find a set of
distinctive key-
points
3. Extract and
normalize the
region content
2. Define a region
around each
keypoint
4. Compute a local
descriptor from the
normalized region
5. Match local
descriptors

67. Goals for Keypoints
Detect points that are repeatable and
distinctive

68. Invariant Local Features
Image content is transformed into local feature coordinates that are
invariant to translation, rotation, scale, and other imaging parameters
Features Descriptors

69. Feature extraction: Corners
9300 Harris Corners Pkwy, Charlotte, NC
Slides from Rick Szeliski, Svetlana Lazebnik, and Kristin Grauman

70. Many Existing Detectors
Available
K. Grauman, B. Leibe
Hessian & Harris [Beaudet ‘78], [Harris ‘88]
Laplacian, DoG [Lindeberg ‘98], [Lowe 1999]
Harris-/Hessian-Laplace [Mikolajczyk & Schmid
‘01]
Harris-/Hessian-Affine [Mikolajczyk & Schmid ‘04]
EBR and IBR [Tuytelaars & Van Gool ‘04]
MSER [Matas ‘02]
Salient Regions [Kadir & Brady ‘01]
Others…

71. Corner Detection: Basic Idea
• We should easily recognize the point by
looking through a small window
• Shifting a window in any direction should
give a large change in intensity
“edge”:
no change
along the
edge direction
“corner”:
significant
change in all
directions
“flat”
region:
no change
in allSource: A. Efros

72. Corner Detection: Mathematics
 
2
,
( , ) ( , ) ( , ) ( , )
x y
E u v w x y I x u y v I x y   
Change in appearance of window w(x,y)
for the shift [u,v]:
I(x, y)
E(u, v)
E(3,2)
w(x, y)

73. Corner Detection: Mathematics
 
2
,
( , ) ( , ) ( , ) ( , )
x y
E u v w x y I x u y v I x y   
I(x, y)
E(u, v)
E(0,0)
w(x, y)
Change in appearance of window w(x,y)
for the shift [u,v]:

74. Corner Detection: Mathematics
 
2
,
( , ) ( , ) ( , ) ( , )
x y
E u v w x y I x u y v I x y   
IntensityShifted
intensity
Window
function
orWindow function w(x,y) =
Gaussian1 in window, 0 outside
Source: R. Szeliski
Change in appearance of window w(x,y)
for the shift [u,v]:

75. Corner Detection: Mathematics
 
2
,
( , ) ( , ) ( , ) ( , )
x y
E u v w x y I x u y v I x y   
We want to find out how this function behaves for
small shifts
Change in appearance of window w(x,y)
for the shift [u,v]:
E(u, v)

76. Corner Detection: Mathematics
 
2
,
( , ) ( , ) ( , ) ( , )
x y
E u v w x y I x u y v I x y   
Local quadratic approximation of E(u,v) in the
neighborhood of (0,0) is given by the second-order
Taylor expansion:



















v
u
EE
EE
vu
E
E
vuEvuE
vvuv
uvuu
v
u
)0,0()0,0(
)0,0()0,0(
][
2
1
)0,0(
)0,0(
][)0,0(),(
We want to find out how this function behaves for
small shifts
Change in appearance of window w(x,y)
for the shift [u,v]:

77. 





 yyyx
yxxx
IIII
IIII
yxwM ),(
x
I
Ix



y
I
Iy



y
I
x
I
II yx





Corners as distinctive interest points
2 x 2 matrix of image derivatives (averaged in
neighborhood of a point).
Notation:

78. Corner response function
“Corner”
R > 0
“Edge”
R < 0
“Edge”
R < 0
“Flat”
region
|R| small
2
2121
2
)()(trace)det(   MMR
α: constant (0.04 to 0.06)

79. Harris corner detector
1) Compute M matrix for each image window to
get their cornerness scores.
2) Find points whose surrounding window gave
large corner response (f> threshold)
3) Take the points of local maxima, i.e., perform
non-maximum suppression
C.Harris and M.Stephens. “A Combined Corner and Edge Detector.”
Proceedings of the 4th Alvey Vision Conference: pages 147—151, 1988.

80. Harris Detector [Harris88]
• Second moment
matrix









)()(
)()(
)(),( 2
2
DyDyx
DyxDx
IDI
III
III
g



83
1. Image
derivatives
2. Square of
derivatives
3. Gaussian
filter g(I)
Ix Iy
Ix
2 Iy
2
IxIy
g(Ix
2
) g(Iy
2
) g(IxIy)
222222
)]()([)]([)()( yxyxyx IgIgIIgIgIg  
 ])),([trace()],(det[ 2
DIDIhar 
4. Cornerness function – both eigenvalues are strong
har5. Non-maxima suppression
1 2
1 2
det
trace
M
M
 
 

 
(optionally, blur first)

81. Harris Detector: Steps

82. Harris Detector: Steps
Compute corner response R

83. Harris Detector: Steps
Find points with large corner response: R>threshold

84. Harris Detector: Steps
Take only the points of local maxima of R

85. Harris Detector: Steps

86. 89
of
65
Epipolar geometry
• the 3D points P, C1,C2 and the projected
points p1, p2 are all located within one common plane
• This common plane denoted π is known as
the epipolar plane

87. 90
of
65
Epipolar geometry
• The epipolar plane is the plane defined by a 3D
point and the two cameras centers.
• The epipolar line is the line determined by the
intersection of the image plane with the epipolar
plane.
• The baseline is the line going through the two
cameras centers.
• The epipole is the image-point determined by the
intersection of the image plane with the baseline.
• the epipole corresponds to the projection of the
first camera center (say C1) onto the second
image plane (say I2), or vice versa.

88. 91
of
65
Epipolar Lines – Example

89. 92
of
65
What is Mosaic and Mosaicing?
• “Mosaic“ originates from an old Italian word
“mosaico” which means a picture or pattern
produced by arranging together small pieces of
stone, tile, glass, etc.
• Mosaicing is the process of assembling a series of
images and joining them together to form a
continuous seamless photographic representation
of the image surface.
• The result is an image with a field of view greater
than that of a single image

90. 93
of
65
Why We Need Image
Mosaicing?
Image mosaicing not only allow you to create a large
field of view using normal camera, the result image
can also be used for texture mapping of a 3D
environment such that users can view the
surrounding scene with real images.

91. 94
of
65
image mosaicing:
Basically there are two main algorithms of image mosaicin
2)Bi-directional Scanning
1)Unidirectional Scanning

92. 95
of
65
Richard Szeliski Image Stitching 95
RANSAC motion model

93. 96
of
65
Richard Szeliski Image Stitching 96
RANSAC motion model

94. 97
of
65
Richard Szeliski Image Stitching 97
RANSAC motion model