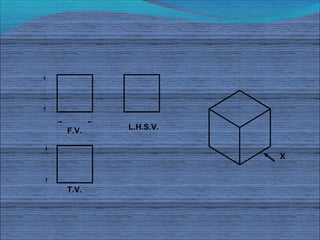
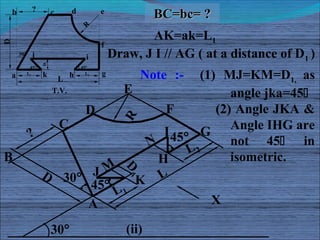
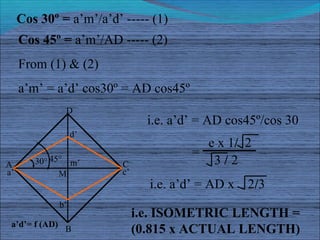
The document discusses isometric projections and isometric drawing. It begins by explaining the limitations of orthographic views and how isometric projections show all three dimensions of an object in a single view. It then defines the principles and types of projection, including orthographic, pictorial, axonometric, isometric, dimetric and trimetric. The remainder of the document focuses specifically on isometric projection, defining isometric axes, lines, planes and drawings. It provides examples of how to construct isometric views of various objects from their orthographic projections.

1. ISOMETRIC
PROJECTIONS
AND
ISOMETRIC
DRAWING

2. Introduction
Orthographic view shows only two dimensions in
any particular view. This makes it difficult to
interpret them and only technically trained person
can interpret the meaning of these orthographic
views.
A non-technical person Can not imagine the shape
of the object from orthographic projections.
Whereas, pictorial projections can be easily
understood even by persons Without any technical
training because such views show all the three
Dimensions Of an object in the same view.

3. But pictorial view does not show the true shape
and size of any principal surface of An object and
it does not show the hidden portions.
Pictorial projections are easy to imagine so these
are used in sales literature.

4.  Principle of Projection :
If straight lines are drawn from various points
of an object to meet a plane then it is said that
object is Projected on that plane.
These straight lines from the object to the
plane are called projectors.
The figure formed by joining the points at
which the projectors meet the plane is called
Projection of that object.

5. Types of Projection:
I) Orthographic Projection
II) Pictorial Projection
Pictorial Projection :
The projection in which the length , height
And depth are shown in one view is
called Pictorial Projection.
Types of Pictorial Projection:
I) Axonometric
II) Oblique
III) Perspective

6. Axonometric Projection:
When projection is obtained on plane inclined to
all the three principal planes, then It is called
Axonometric projection.
Types of Axonometric projection:
sometric
Dimetric
Trimetric

7. Isometric Projection :
The projection is obtained on a plane which is
equally inclined to all the three principal planes.
Isometric Projections and Isometric drawings are
represented on the plane paper or sheet by drawing
isometric axes, isometric lines and isometric planes.

8. When a cube is kept in particular position then it
gives isometric axes, isometric lines and isometric
planes.
Particular position : When cube is resting on H.P.
on corner G and diagonal EC is Perpendicular to
A
V.P.
B D
E C
F H
30o 30o
M G N Base Line

9. Isometric Axes :
The three lines CB,CD and CG meeting at the point
C and making angle of 120 degree with each other
are called isometric axes.
Isometric lines:
The lines parallel to isometric axes are called
isometric lines.
Isometric planes:
The planes represented by faces of cube are called
isometric planes.
Similarly any planes parallel to these planes are also
called isometric planes.

10. Isometric drawing or isometric view:
The pictorial view drawn with true scale is called
Isometric drawing or isometric view.
Isometric projection:
The pictorial view drawn with the use of isometric
scale is called Isometric projection.

11. F.V. L.H.S.V.
X
T.V.

12. Aim:- Figure-1, shows the F.V. & T.V. of a simple
vertical rectangular plane of size LH. Draw its
isometric view, for (a) R.H.S.V. & (b) L.H.S.V.
a’ b’
H
d’ L c’
F.V.
a b
d T.V. c
Figure-1

13. MN, is the base line for isometric axes.
PQ, is the isometric axis (vertical) for Fig.1(a)
PR, is the isometric axis ( horizontal),for R.H.S.V. for
Fig.1(a) at 30º with base line MN.
Q
A
Note:- The diagonal line
R a’c’ in ortho. View
B
increases in its iso. View
D
(Fig.1-a), as AC (known
H
L
as, non isometric line)
X C
M N
Figure-1(a) P

14. MN, is the base line for isometric axes.
PQ, is the isometric axis (vertical) for Fig.1(b)
PS, is the isometric axis ( horizontal),for L.H.S.V. for
Fig.1(b) at 30º with base line MN.
Q
B
Note:- The diagonal line
a’c’ in ortho. View S
decreases in its iso. View A
(Fig. 1-b), as AC (known C
as, non isometric line) H L
D X
M Figure-1(b) N
P

15. Figure shows the Top View of a rectangular plane of
100 x 70. Draw its isometric view i) for R.H.S.V & ii)
for L.H.S.V.
a b
70
d c
100
T.V.

16. A
70 10
0
D
B
X C
30° 30°
ISOMETRIC VIEW OF THE HORIZONTAL
RECTANGULAR PLANE (100 X 70) for its
R.H.S.V.

17. B
100
C
A
70
D X
30° 30°
ISOMETRIC VIEW OF THE HORIZONTAL
RECTANGULAR PLANE (100 X 70) for its
L.H.S.V.

18. c’
d’ c’
M1
C2 C3
d’ N2
a’ b’ M2 b’ C1
C4
N1
X
a b a’

19. ISOMETRIC VIEW OF SIMPLE PLANES
Aim:-Figure shows the F.V.of a cut
geometric plane.Draw its Isometric
view . (i)For R.H.S.V. & (ii)For L.H.S.V.
?
b’ c’
a’
30° d’
H
R
g’ L f’ e’
F.V.

20. ?
b’ c’
Darken the required arc FD a’
with center C2 d’
30°
H
R
g’ L f’ e’
A L
? -: Solution :-
B
AB=a’ b’ ED=EF=R
H
30° R
2 C Now, only the
R Quadrant of a circle
G D R
1
C2
(L.H.S. upward), is to
F C3 be drawn using Four
X E center method.
C1
C4
(i) 30°

21. ?
b’ c’
a’
30° d’
H
R
g’ L f’ e’
L C
? B D
A
30° E
H
F
G
X
30° (ii)

22. Aim:-Figure shows the T.V. of a cut geometric
plane. Draw its Isometric, (i)For R.H.S.V.
& (ii) For L.H.S.V.
b ? c d
e
R
f
D
30° j i
D1
45° 45°
a L1 k h L2 g
L
T.V.

23. ?
b c d e
BC=bc= ? ED=EF=R
R
AK=ak=L1 GH=gh=L2
D
f
30° j i Draw, J I // AG ( at a distance of D1 )
D1
45° 45°
a L1 k
L
h L2 g Note :- (1) MJ=KM=D1, as
T.V.
B angle jka=45
? (2) Angle JKA &
D
C Angle IHG are not
30° D 45 in isometric.
A 45° J M
L
1
D1 R E
K N
L H I
L 45° F
2
X G
(i)
30°

24. ?
b c d e
BC=bc= ?
R
AK=ak=L1
D
f
30° j i Draw, J I // AG ( at a distance of D1 )
D1
45° 45°
a L1 k
L
h L2 g Note :-
(1) MJ=KM=D1, as
E
T.V.
angle jka=45
D F (2) Angle JKA &
?
C
I 45° G R
Angle IHG are
N not 45 in
L2
B H isometric.
J M
D1
D 30° K L
45° 1
L
A X
30° (ii)

25. C2’
F.V. C2
C1’
C1
T.V.

26. d
4 3
e c
3’
d’
1 a c’
b 2 4’
e’ 3
2’
b’ d
a’ c
4
1’
e 2
b
a
1

27. C2’ C3’
c’
M1
C4’ C2 d’ N2
C3
T.V. M2 b’
C4 C1
N1 X
a’
F.V.

38. Draw the Iso.View of a
regular Pentagonal plane
X a’ b’ c’ Y
of 40mm sides, with one
e’ d’
90° side normal to V.P. & the
s d r plane is in H.P.
e
g
40
c
R
a D
p b q C
2D S G Q
E
40 B
A X
P 3D

39. O’ Draw the Iso.View of a
Pentagonal Pyramid, having
60
base sides 40mm, axis 60mm
X a’ g’ b’ c’ Y long,when its base is in
e’ d’ H.P.with a side of it normal
d to V.P.
e O
60
O g c
40
R
a D
C
b
G
2D S Q
E
40 B
A X
3D

40. Aim:- Figure shows the orthographic
projections of a cut simple block. Draw its
appropriate Pictorial ( Isometric ) view,
giving the dimensions.
NOTE: The appropriate Isometric will
be,considering its R.H.S.V.
( which is not given & is to be added as a
missed view).

41. A
a
55
15 20
B b c d
55 60
R.H.S.V. F.V.
Normally, dotted lines 30
are not drawn in Iso.
20
View, unless 1 2
specifically required
55
to reveal the object 3 T.V.
perfectly.
Figure 15 15

42. 20 30 ISOMETRIC
VIEW
1
20
55
a
15 20
40
A
b c d a 2
60
F.V.
30
35
20
1 2 15 3
b c B
55
3
15
30
15 T.V. 15 d 55
15
X
NOTE:- IN R.H.S.MISSED VIEW, THE AREAS, A & B ARE
SEEN AND IS DRAWN IN ITS CORROSPONDING
SPACE

43. Figure shows Front View
and Top View of a machine
parts. Sketch its isometric
view & dimension it.

44. SQ.HOLE OF 20
R25
C
B 30°
A D
20
70
30
20
F.V.
b2
20 10 20
a
c
b1
10
70 20
T.V.

45. ISOMETRIC VIEW
SQ.HOLE OF 20
a
25
10
C
95 c
B
A 20 30° b2
b1
20
30
25 D
20
11
5
20 50
X

46. Aim:- Figure shows the F.V. & T.V. of a machine
component.
Figure
20
Draw its
R3
0
15
pictorial
F.V.
(ISOMETRIC) 20
view, giving
15
30
30
the
dimensions. R10
15
20
120 40
T.V.

47. Note 1:- The machine component is splitted
into four different parts, for its iso.
sketching, with bottom base part as first
drawn.
Note 2:-The circularity or part of that of
Ortho.View, is to be drawn in Iso view as an
ellipse or part of that using “four center
method”,as explained earlier.
Note 3:- Such components may be drawn in
iso., by area (plane)wise w.r.t F.V, T.V &
S.V directions. Never prefer “box method”
for such components.

48. 20
Split-II Solution
60
See, Note 2
20
20
Split-III
15 R3
0
20 Split-IV
65
15
ISOMETRIC R1
0
VIEW 30
30 120 Split-I
See, Note 2 15

49. ISOMETRIC SCALE
70
(To be used for isometric projections) )
e 60
in
° l 50
45
( on 40
TH
G 30 e)
EN lin
L 20 0°
A
L
(o n3
TU 10 60 TH √3)
A
C P N G √2 /
0 40 C LE BY
-5 R I ED
-10 20 ET C
OM EDU
IS (R
Q
B 45°
30° 90°
A
BASE LINE

50. III. A
The Front View of the Top Face of a Cube having
edges “e” (with one of the body diagonal line, normal
D to V.P. ) is to be treated
as ISOMETRIC of the
Top Face of the Cube
d’ (with a side parallel to
V.P.)
A 30° 45° m’ C All the edges Top face
a’ M c’
edges, base face edges
and 4 vertical edges of
b’ the cube are reduced in
its isometric view, in
a’d’= f (AD) the stated condition.
B

51. Cos 30º = a’m’/a’d’ ----- (1)
Cos 45º = a’m’/AD ----- (2)
From (1) & (2)
a’m’ = a’d’ cos30º = AD cos45º
D
i.e. a’d’ = AD cos45º/cos 30
d’
e x 1/ 2
=
A 30° 45° m’ C 3/2
a’ M c’
i.e. a’d’ = AD x 2/3
b’
i.e. ISOMETRIC LENGTH =
a’d’= f (AD)
B (0.815 x ACTUAL LENGTH)

52. Aim:- Sketch shows the Orthographic
views of a machine component. Draw
its appropriate Isometric view, using
“splitting the object into pieces”
techniques. Give the dimensions on
the ISOMETRIC VIEW drawn.

53. 90
20 50 R40 Sketch
40 20
30
20
φ40
T.V.
10
30 R.H.S.V.
80 (missed view)
may be added
here in height
20
& depth range
F.V.

54. Dimensions
20
must be C
10
given on the
Isometric 25
50
30
view, which 30
are not 20
50 40
shown here. B
20
80
20
Ø30
70
R4 0
R15
25 20
90 80x80
20
25
A square D

55. Exercise
Figure shows the Orthographic
views of a machine component.
Draw its Isometric view.
Give the dimensions as per
aligned system.

56. Ø30 R30
c
25 60
B
15
35
40
15
60
b
a 20 A
10
40 120
80
L.H.S.V. FRONT VIEW
FIGURE
NOTE:- The front view areas are A & B,
while the side view areas are a, b & c.

57. Solution
ø30
R30
20 B
60
25
c
15 20
35
15 40
20
b
10
a
40 A 120
80
ISOMETRIC X
VIEW

58. F.V. L.H.S.V.

59. c1’

61. 34
60
25
L= 60 mm
H= 25 mm
D= 34 mm X