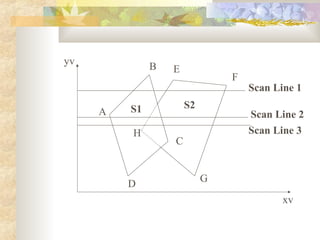
This document discusses methods for identifying and removing hidden surfaces when rendering 3D scenes to create a realistic 2D image. It describes two approaches: object-space methods that compare whole objects, and image-space methods that decide visibility point-by-point. It focuses on the depth buffer/z-buffer method, which processes surfaces one point at a time, comparing depth values to determine visibility and store the color of visible points. It also discusses using scan line coherence to solve hidden surfaces one scan line at a time from top to bottom.

1. Hidden Surfaces

2. Introduction
When we view a picture containing non
transparent objects and surfaces, then we
can’t see those objects from view which
are behind from the objects closer to eye.
We must remove these hidden surfaces to
get realistic screen image. The
identification & removal of these surfaces
is called the Hidden- surface problem.

3.  Two approaches for Visible surface
detection are:
(i) Object-space methods: compares objects
& parts of objects to each other within the
scene definition to determine which surfaces,
as a whole, we should label as visible.
(ii) Image-space methods: visibility is
decided point by point at each pixel position
on the projection plane.

4. Depth Comparisons
 Also known as Depth Buffer Method or z-
buffer method, since object depth is usually
measured from the view plane along z-axis.
 Each surface of a scene is processed
separately, one point at a time across the
surface.
 Method is applied to scenes containing
polygon surfaces.

5.  Object descriptions converted to projection
coordinates, each (x,y,z) position on a
polygon surface corresponds to the
orthographic projection point (x,y) on the
view plane.
xv
S3
S2
S1
xv
(x,y)
zv

6.  Depth Buffer algo. is implemented in
normalized coordinates.
 Two buffer areas are required.
(i) A depth buffer is used to store depth
values for each (x,y) position as surfaces
are processed.
(ii) A refresh buffer stores the intensity
value for each position.
 Initially, Depth buffer = 0(min depth)
refresh buffer = background intensity.

7.  Each surface is then scanned, calculating
the depth(z value) at each (x,y) pixel
position.
 Calculated depth value is compared to
previous one stored in buffer.
 If calculated value is greater than the value
stored in the depth buffer, then the new
depth value is stored, & intensity at the
position is placed in the refresh buffer.

8.  Depth values for a surface position (x,y)
are calculated from the plane equation for
each surface:
z = -Ax – By –D
C
 Equation for a plane surface is:
Ax + By + Cz + D = 0
Where x,y,z are any point on the plane and
A,B,C & D are constant coefficients
describing properties of plane.

9.  Scan line coherence method solves the
hidden surface problem one scan line at a
time from top to bottom.
 The simplest scan line algorithm is a one
dimensional version of the Depth Buffer.
 Across each scan line, depth calculations
are made for each overlapping surface to
determine which is nearest to the view
plane.

10. yv B E
F
Scan Line 1
S1 S2
A Scan Line 2
H Scan Line 3
C
G
D
xv

11.  When visible surface has been determined,
the intensity value for that position is
entered into refresh buffer.
 Define a flag, for each surface that is set on
& off to indicate whether a position along
scan line is inside or outside of the surface.
 Active List for scan line 1contains info
about edges AB,BC,EH, & FG. Between
edges AB & BC,only the flag for surface
S1 is on. No depth calculation requires

12. & refresh buffer contains intensity value for
S1. Similarly between EH & FG.
 For scan line 2, active edge list contain
AD, BC, EH & FG. Between the edge AD
& EH only the flag of S1 is on. But b/w EH
& BC, the flag for both surfaces are on. In
this interval depth calculations must be
made.
 For scan line 3, we can take advantage of
coherence(regularities in a scene) as we
pass to next scan line.