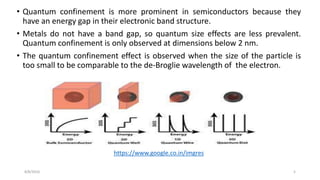
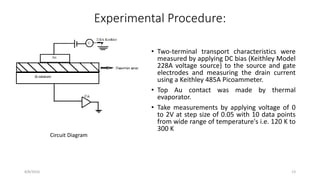
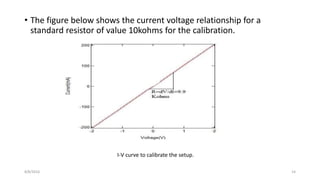
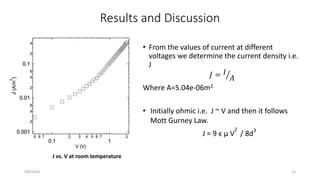
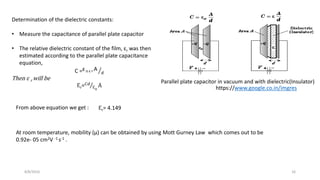
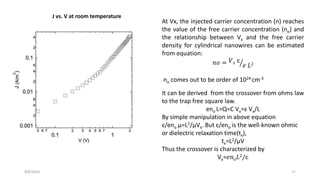
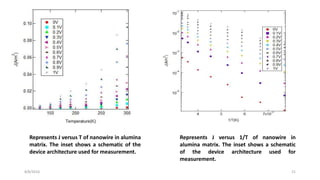
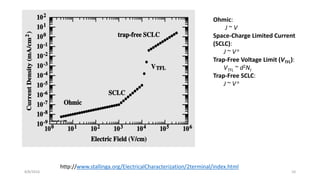
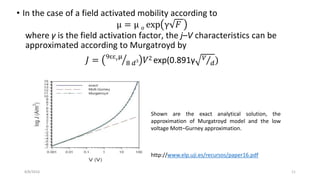
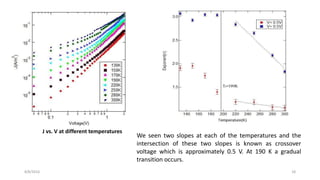
The document summarizes research on understanding charge transport in low dimensional semiconductor nanostructures embedded in an insulating matrix. Specifically, it examines current-voltage characteristics of germanium nanowire arrays in an alumina matrix as a function of temperature. Key findings include: 1) At room temperature, conduction follows Ohm's law at low voltages and Mott-Gurney's space charge limited current law at higher voltages. 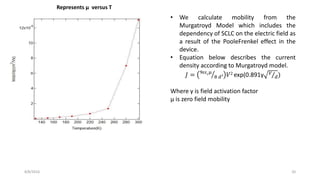2) With decreasing temperature, conduction transitions from a trap-free regime to an exponentially distributed trap regime. 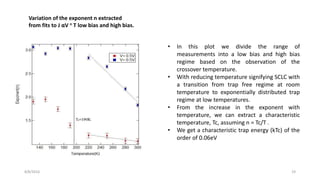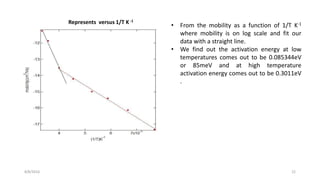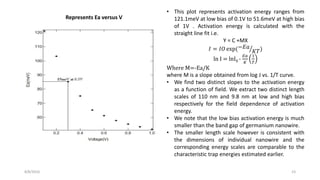3) Mobility decreases with decreasing temperature, and activation energy is extracted from an Arrhenius plot, found to be 85 meV at low temperatures and 301 meV

1. Understanding Charge Transport In Low Dimensional
Semiconductor Nano-structures In An Insulating Matrix
BY:
NIKITA GUPTA
Under the supervision of
Dr. Nirat Ray(SPS,JNU)
Dr. Shipra Mital Gupta(USBAS)

2. Objective
• To find out the current voltage characteristics of germanium (Ge)
nanowire arrays in Al2O3 matrix, as a function of temperature.
8/8/2016 2

3. Semiconductors
• A Semiconductor is a material which has Electrical Conductivity
between that of conductor and that of an insulator.
8/8/2016 3

4. Quantum Confinement
• Quantum confinement is the spatial confinement of electron hole pairs in one or more
dimensions within a material.
-1 D confinement-quantum wells
-2D confinement- quantum wires
-3D confinement-quantum dot
• Electron hole pairs become spatially confined when the diameter of a particle approaches the de
Broglie wavelength of electrons in the conduction band.
• As a result the energy difference between energy bands is increased with particle size decreasing.
https://www.google.co.in/imgres
8/8/2016 4

5. • Quantum confinement is more prominent in semiconductors because they
have an energy gap in their electronic band structure.
• Metals do not have a band gap, so quantum size effects are less prevalent.
Quantum confinement is only observed at dimensions below 2 nm.
• The quantum confinement effect is observed when the size of the particle is
too small to be comparable to the de-Broglie wavelength of the electron.
https://www.google.co.in/imgres
8/8/2016 5

6. Introduction to Nanowires:
• Diameter of nanowires range from a single atom to a few hundreds of
nanometers.
• They represent the smallest dimension for efficient transport of electrons and
excitons, and thus will be used as interconnects and critical devices in Nano
electronics and nano-optoelectronics.”
• Length varies from a few atoms to many microns. Different name of quantum
wires in literature:
• Whiskers, fibers: 1D structures ranging from several nanometers to several
hundred microns
• Nanowires: Wires with large aspect ratios (e.g. >20),
• Nanorods: Wires with small aspect ratios.
• NanoContacts: short wires bridged between two larger electrodes.
8/8/2016 6

7. Conduction Mechanism
• Two types of conduction mechanism:
1) Electrode limited
• Schottky Emission J α V 1/2
2)Bulk limited
• Ohmic conduction J α V
• Space charge limited current J α V n
8/8/2016 7

8. Space Charge Limited Current
• At lower voltages, the current density is given by the Ohmic current
J = n e μ E
• As the applied voltage is increased, the charges tend to accumulate in the region between the
electrodes and the electric field due to the accumulated charge influences the conduction current
• This mechanism is usually referred to as SPACE CHARGE LIMITED CURRENT (SCLC).
and is given by
J = 9 ϵ μ V
2
/ 8d3
This is known as MOTT GURNEY LAW
• SCLC occurs when the rate of recombination of the electrons injected into the conduction band (or
holes into the valence band)exceeds the concentration of the initial charge carriers.
• The SCLC strongly depends on the characteristic parameters of the charge traps.
8/8/2016 8

9. SCLC without traps
• One requirement for SCLC is that one
of the two contacts must be Ohmic
because charge injection shouldn‘t be
limited on that contact. In this case
the contact provides an excess
amount of carriers to the channel.
SCLC with traps (trapped-SCLC)
• In bulk insulating or semiconducting
materials, SCLC is a well-known model
used to describe nonlinear and non-
exponential IV characteristics
• In nanowire systems, charge transport
can be highly affected by trapped-
SCLC because the carrier depletion is
more frequently caused by the surface
states due to high surface-to-volume
ratio. The trap states, mainly on the
surface of the nanowire, can easily be
incorporated during growth.
8/8/2016 9
Here two types of space charge limited current (SCLC) are introduced: trap free SCLC
behavior and trapped-SCLC behavior.

10. 8/8/2016 10
Ohmic:
J ~ V
Space-Charge Limited Current
(SCLC):
J ~ V n
Trap-Free Voltage Limit (VTFL):
VTFL ~ d2Nt
Trap-Free SCLC:
J ~ V n
http://www.stallinga.org/ElectricalCharacterization/2terminal/index.html

11. • In the case of a field activated mobility according to
µ = µ 𝑜 exp γ 𝐹
where γ is the field activation factor, the j–V characteristics can be
approximated according to Murgatroyd by
𝐽 = 9ɛɛ 𝑟
µ
8 𝑑3 𝑉2 exp(0.891γ 𝑉
𝑑)
8/8/2016 11
Shown are the exact analytical solution, the
approximation of Murgatroyd model and the low
voltage Mott–Gurney approximation.
http://www.elp.uji.es/recursos/paper16.pdf

12. Synthesis of Nanowire Arrays
• Three-dimensional continuous networks of Ge nanowires formed by self-assembly process by
magnetron sputter deposition in amorphous Al2O3 matrix by magnetron sputter deposition.
• Pure Ge(99:995) and Al2O3(99:995) were co-deposited on Si(111) substrate at 500οC.
• The networks have body centered tetragonal arrangement of their nodes and highly tunable
nanowire length and arrangement parameters.
• The films have amorphous internal structure of both matrix and Ge after the deposition. The
crystallization may be induced by annealing at 600C in vacuum.
8/8/2016 12
(a) TEM image of the film cross-section,
(b) simulation of the structure x-z view
and (c) corresponding GISAXS map.

13. Experimental Procedure:
• Two-terminal transport characteristics were
measured by applying DC bias (Keithley Model
228A voltage source) to the source and gate
electrodes and measuring the drain current
using a Keithley 485A Picoammeter.
• Top Au contact was made by thermal
evaporator.
• Take measurements by applying voltage of 0
to 2V at step size of 0.05 with 10 data points
from wide range of temperature's i.e. 120 K to
300 K
8/8/2016 13
Circuit Diagram

14. 8/8/2016 14
• The figure below shows the current voltage relationship for a
standard resistor of value 10kohms for the calibration.
I-V curve to calibrate the setup.

15. Results and Discussion
• From the values of current at different
voltages we determine the current density i.e.
J
𝐽 = 𝐼
𝐴
Where A=5.04e-06m2.
8/8/2016 15
• Initially ohmic i.e. J ~ V and then it follows
Mott Gurney Law.
J = 9 ϵ μ V
2
/ 8d3
J vs. V at room temperature

16. 8/8/2016 16
Parallel plate capacitor in vacuum and with dielectric(Insulator)
Ɛr= 4.149From above equation we get :
https://www.google.co.in/imgres
Determination of the dielectric constants:
• Measure the capacitance of parallel plate capacitor
• The relative dielectric constant of the film, ɛr was then
estimated according to the parallel plate capacitance
equation,
C =ɛ o ɛ r A
𝑑
Then ɛ r will be
Ɛr= 𝐶𝑑
Ɛo
A
At room temperature, mobility (µ) can be obtained by using Mott Gurney Law which comes out to be
0.92e- 05 cm2V -1 s-1 .

17. 8/8/2016 17
J vs. V at room temperature
At Vx, the injected carrier concentration (n) reaches
the value of the free carrier concentration (no) and
the relationship between Vx and the free carrier
density for cylindrical nanowires can be estimated
from equation:
𝑛𝑜 = 𝑉 𝑥 ɛ
𝑒 𝐿2
no comes out to be order of 1024 cm-3
It can be derived from the crossover from ohms law
to the trap free square law.
eno L=Q=C Vx=ɛ Vx/L
By simple manipulation in above equation
ɛ/eno µ=L2/µVx. But ɛ/eno is the well-known ohmic
or dielectric relaxation time(tx),
tx=L2/µV
Thus the crossover is characterized by
Vx=𝑒𝑛 𝑜 𝐿2/ɛ

18. 8/8/2016 18
J vs. V at different temperatures
We seen two slopes at each of the temperatures and the
intersection of these two slopes is known as crossover
voltage which is approximately 0.5 V. At 190 K a gradual
transition occurs.

19. 8/8/2016 19
Variation of the exponent n extracted
from fits to J αV n T low bias and high bias.
• In this plot we divide the range of
measurements into a low bias and high bias
regime based on the observation of the
crossover temperature.
• With reducing temperature signifying SCLC with
a transition from trap free regime at room
temperature to exponentially distributed trap
regime at low temperatures.
• From the increase in the exponent with
temperature, we can extract a characteristic
temperature, Tc, assuming n = Tc/T .
• We get a characteristic trap energy (kTc) of the
order of 0.06eV

20. 8/8/2016 20
Represents µ versus T
• We calculate mobility from the
Murgatroyd Model which includes the
dependency of SCLC on the electric field as
a result of the PooleFrenkel effect in the
device.
• Equation below describes the current
density according to Murgatroyd model.
𝐽 = 9ɛɛ 𝑟
µ
8 𝑑3 𝑉2 exp(0.891γ 𝑉
𝑑)
Where γ is field activation factor
µ is zero field mobility

21. 8/8/2016 21
Represents J versus T of nanowire in alumina
matrix. The inset shows a schematic of the
device architecture used for measurement.
Represents J versus 1/T of nanowire in
alumina matrix. The inset shows a schematic
of the device architecture used for
measurement.

22. 8/8/2016 22
• From the mobility as a function of 1/T K-1
where mobility is on log scale and fit our
data with a straight line.
• We find out the activation energy at low
temperatures comes out to be 0.085344eV
or 85meV and at high temperature
activation energy comes out to be 0.3011eV
.
Represents versus 1/T K -1

23. 8/8/2016 23
Represents Ea versus V
• This plot represents activation energy ranges from
121.1meV at low bias of 0.1V to 51.6meV at high bias
of 1V . Activation energy is calculated with the
straight line fit i.e.
Y = C +MX
𝐼 = 𝐼𝑂 exp(−𝐸𝑎
𝐾𝑇)
ln I = lnI0 -
𝐸𝑎
𝐾
1
𝑇
Where M=-Ea/K
where M is a slope obtained from log J vs. 1/T curve.
• We find two distinct slopes to the activation energy
as a function of field. We extract two distinct length
scales of 110 nm and 9.8 nm at low and high bias
respectively for the field dependence of activation
energy.
• We note that the low bias activation energy is much
smaller than the band gap of germanium nanowire.
• The smaller length scale however is consistent with
the dimensions of individual nanowire and the
corresponding energy scales are comparable to the
characteristic trap energies estimated earlier.

24. • From the above graphs J-V curves were measured over a wide temperature range, from 130 K to 280 K,
with applied potentials 2V .
• Higher voltages generally degraded the devices and were avoided.
• The Ge nanowire device exhibited non- linear IV curves as seen from above graphs. The nanowire
conductance increased with increasing temperature, and the J-V curves became increasingly linear at
higher temperature.
• We have shown how to control the contact properties of nanowires by suitable treatment of the electrode-
nanowire interface. We have analyzed the charge carrier transport in nanowires. The SCLC conduction
mechanism is found to dominate at temperatures below 190 K. By a careful analysis of IVCs affected by
SCLC, we have been able to determine the shallow charge traps with an exponential distribution of energy
with a concentration of the order of 1*1024cm-3. This could enhance the on/off ratio of the resistive
switching.
• The understanding of nanowire transport properties at different temperatures is critical for their
integration in electronic devices. The observation of the SCLC mechanism enables further investigations for
nanowires application in the resistive switching device. We believe that the advancement of these
techniques will be beneficial for integration of bottom-up grown nanowires in large scale devices showing
SCLC at room temperature.
8/8/2016 24
Conclusion

25. References
• Fu-Chien Chiu "A Review on Conduction Mechanisms in Dielectric Films". Department of Electronic
Engineering, Ming Chuan University, Taoyuan 333,Taiwan.
• R Miranti,C Krause, J Parisi and H Borchert "Charge transport through thin films made of colloidal
CuInS2 nanocrystals". University of Oldenburg, Department of Physics, Energy and Semiconductor
Research Laboratory, Carlvon-Ossietzky-Str. 9-11, D-26129 Oldenburg, Germany.
• Gunta Kunakova, Roman Viter, Simon Abay, Subhajit Biswas, Justin D.Holmes, Thilo Bauch, Floriana
Lombardi and Donats Erts "Space charge limited current mechanism in Bi2S3 nanowires". Citation:
Journal of Applied Physics 119; 114308(2016); doi: 10:1063=1:4944432.
• Angel Mancebo "Current-Voltage Characteristics for p-i-p Diodes". Department of Physics, University
of Florida, Gainesville, FL 32611.
• Dongkyun Ko "Charge transport properties in semiconductor nanowires". The Ohio State
University,2011 Dissertation.
8/8/2016 25

26. 8/8/2016 26
THANK YOU!!