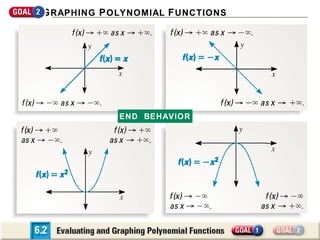
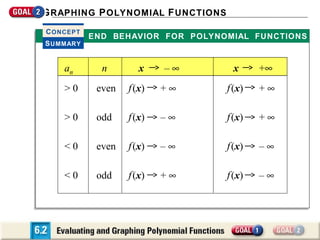
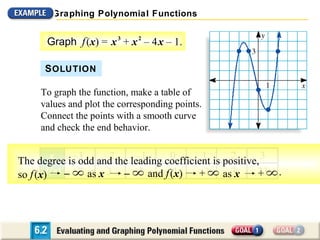
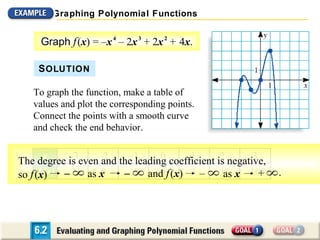
The document discusses evaluating and graphing polynomial functions, which are functions of the form f(x) = anxn + an-1xn-1 + ... + a1x + a0, where the exponents are whole numbers. It provides information on identifying polynomial functions, evaluating them using synthetic substitution, and graphing them by examining end behavior as x approaches positive or negative infinity. Common types of polynomial functions include constant, linear, quadratic, and cubic functions.

1. E VALUATING P OLYNOMIAL F UNCTIONS
A polynomial function is a function of the form
f (x) = an x nn + an – 1 x nn––1 1 · ·+ a 1 x + a 0 a 0
+·
n
0
Where an ≠ 0 and the exponents are all whole numbers.
n
For this polynomial function, an is the
an
constant term
a
a 00 is the constant term, and n is the
n
leading coefficient
leading coefficient,
degree
degree.
A polynomial function is in standard form if its terms are
descending order of exponents from left to right.
written in descending order of exponents from left to right.

2. E VALUATING P OLYNOMIAL F UNCTIONS
You are already familiar with some types of polynomial
functions. Here is a summary of common types of
polynomial functions.
Degree
Type
Standard Form
0
Constant
f (x) = a 0
1
Linear
f (x) = a1x + a 0
2
Quadratic
f (x) = a 2 x 2 + a 1 x + a 0
3
Cubic
f (x) = a 3 x 3 + a 2 x 2 + a 1 x + a 0
4
Quartic
f (x) = a4 x 4 + a 3 x 3 + a 2 x 2 + a 1 x + a 0

3. Identifying Polynomial Functions
Decide whether the function is a polynomial function. If it is,
write the function in standard form and state its degree, type
and leading coefficient.
f (x) =
1 2
x – 3x4 – 7
2
S OLUTION
The function is a polynomial function.
Its standard form is f (x) = – 3x 4 +
1 2
x – 7.
2
It has degree 4, so it is a quartic function.
The leading coefficient is – 3.

4. Identifying Polynomial Functions
Decide whether the function is a polynomial function. If it is,
write the function in standard form and state its degree, type
and leading coefficient.
f (x) = x 3 + 3 x
S OLUTION
The function is not a polynomial function because the
x
term 3 does not have a variable base and an exponent
that is a whole number.

5. Identifying Polynomial Functions
Decide whether the function is a polynomial function. If it is,
write the function in standard form and state its degree, type
and leading coefficient.
–
f (x) = 6x 2 + 2 x 1 + x
S OLUTION
The function is not a polynomial function because the term
2x –1 has an exponent that is not a whole number.

6. Identifying Polynomial Functions
Decide whether the function is a polynomial function. If it is,
write the function in standard form and state its degree, type
and leading coefficient.
f (x) = – 0.5 x + π x 2 –
2
S OLUTION
The function is a polynomial function.
Its standard form is f (x) = π x2 – 0.5x –
2.
It has degree 2, so it is a quadratic function.
The leading coefficient is π.

7. Identifying Polynomial Functions
Polynomial function?
f (x) = 1 x 2 – 3 x 4 – 7
2
f (x) = x 3 + 3x
f (x) = 6x2 + 2 x– 1 + x
f (x) = – 0.5x + π x2 –
2

8. Using Synthetic Substitution
One way to evaluate polynomial functions is to use
direct substitution. Another way to evaluate a polynomial
is to use synthetic substitution.
Use synthetic division to evaluate
f (x) = 2 x 4 + −8 x 2 + 5 x − 7 when x = 3.

9. Using Synthetic Substitution
S OLUTION
2 x 4 + 0 x 3 + (–8 x 2) + 5 x + (–7)
Polynomial
Polynomial inin
standard form
standard form
3•
3
2
0
–8
5
–7
Coefficients
6
18
30
105
6
10
35
98
x-value
2
The value of (3) is the last number you write,
The value of ff(3) is the last number you write,
In the bottom right-hand corner.
In the bottom right-hand corner.

10. G RAPHING P OLYNOMIAL F UNCTIONS
The end behavior of a polynomial function’s graph
is the behavior of the graph as x approaches infinity
(+ ∞) or negative infinity (– ∞). The expression
x
+ ∞ is read as “x approaches positive infinity.”

11. G RAPHING P OLYNOMIAL F UNCTIONS
END BEHAVIOR

12. G RAPHING P OLYNOMIAL F UNCTIONS
C ONCEPT
END BEHAVIOR FOR POLYNOMIAL FUNCTIONS
S UMMARY
x
+∞
+∞
f (x)
+∞
f (x)
–∞
f (x)
+∞
even
f (x)
–∞
f (x)
–∞
odd
f (x)
+∞
f (x)
–∞
an
n
x
>0
even
f (x)
>0
odd
<0
<0
–∞

13. Graphing Polynomial Functions
Graph f (x) = x 3 + x 2 – 4 x – 1.
S OLUTION
To graph the function, make a table of
values and plot the corresponding points.
Connect the points with a smooth curve
and check the end behavior.
x
–3
–2
–1
0
1
2
The degree is odd and the leading coefficient is positive, 3
–3 as3x
23
+
+
(x)
so f (x)f(x) – –7 as x 3 – 3 and f–1
.

14. Graphing Polynomial Functions
Graph f (x) = –x 4 – 2x 3 + 2x 2 + 4x.
S OLUTION
To graph the function, make a table of
values and plot the corresponding points.
Connect the points with a smooth curve
and check the end behavior.
x
0
1
2
3
The degree –3even–2 the leading coefficient is negative,
is
and –1
f (x) –
–21 as x
0
0
––1 and f (x) 3 – –16 x –105
+
as
so f (x)
.

15. Assignment