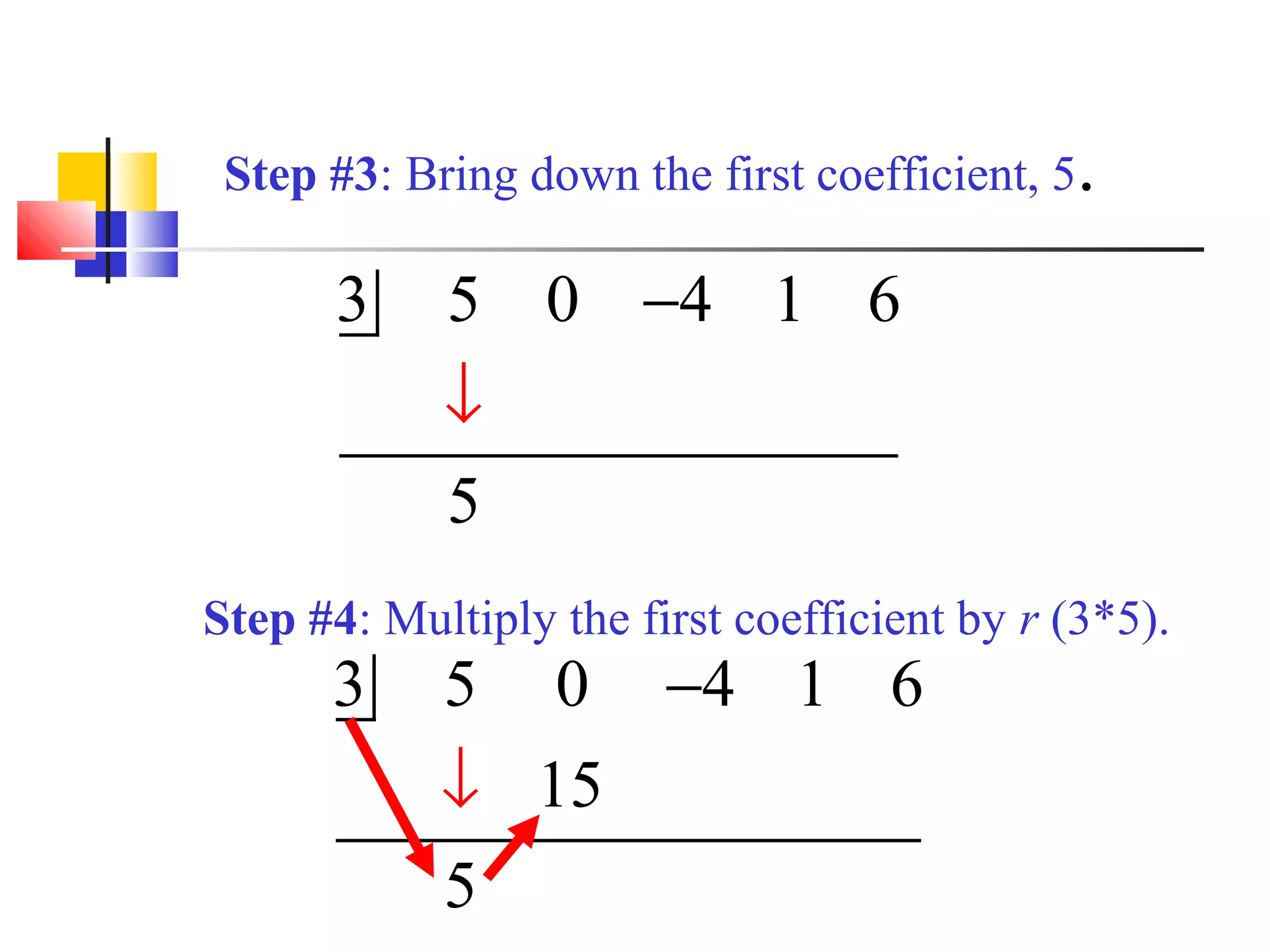
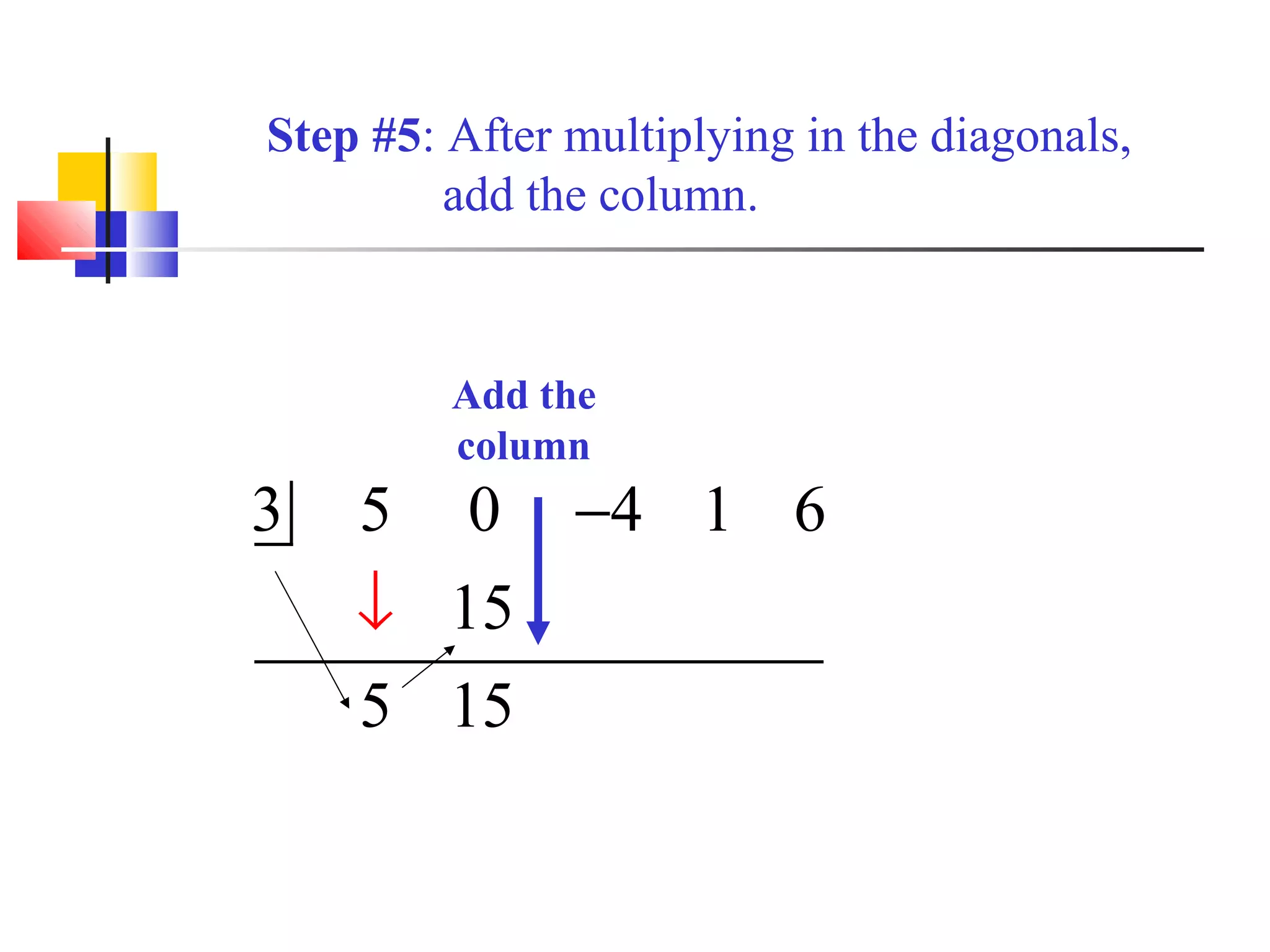
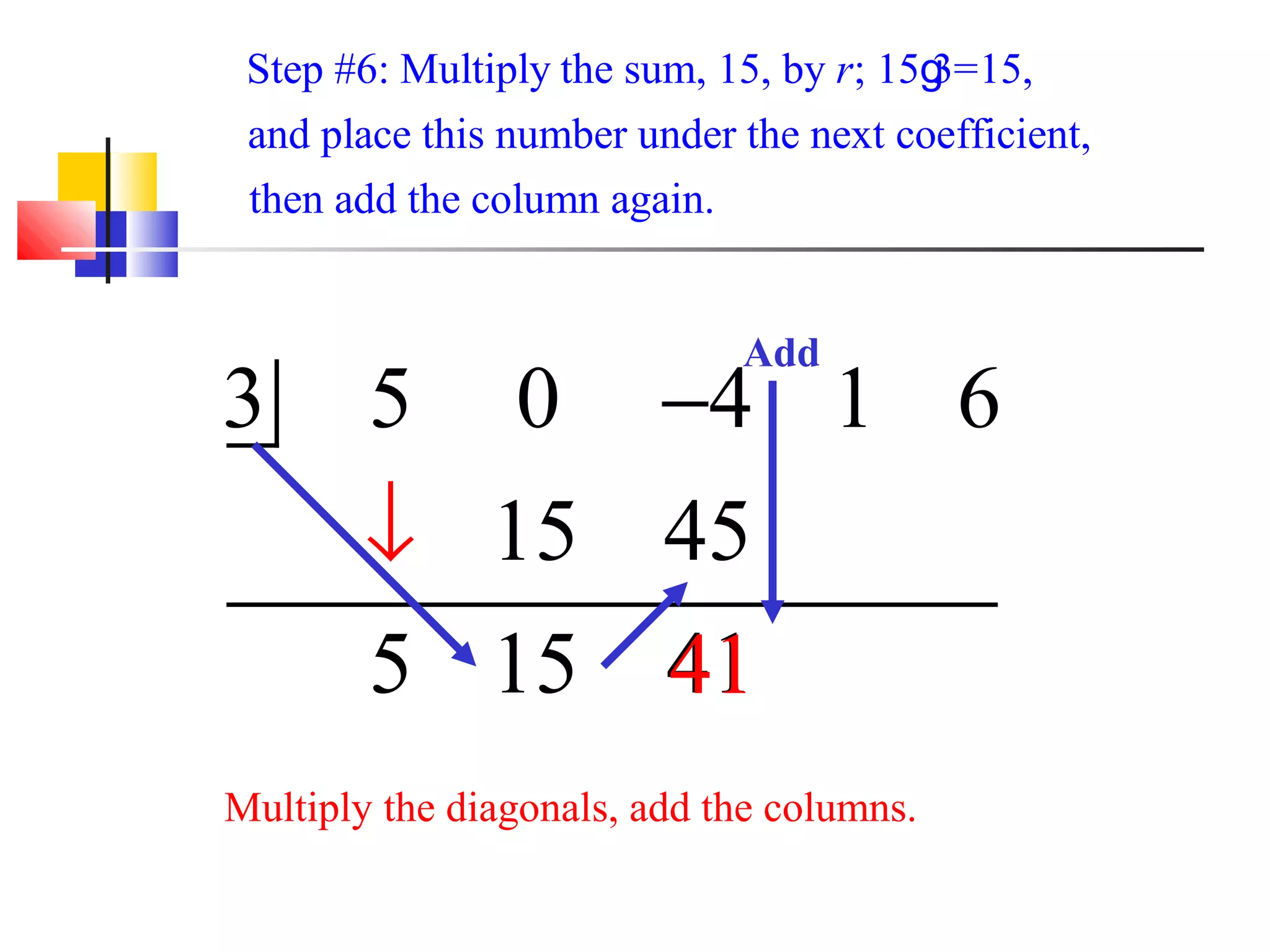
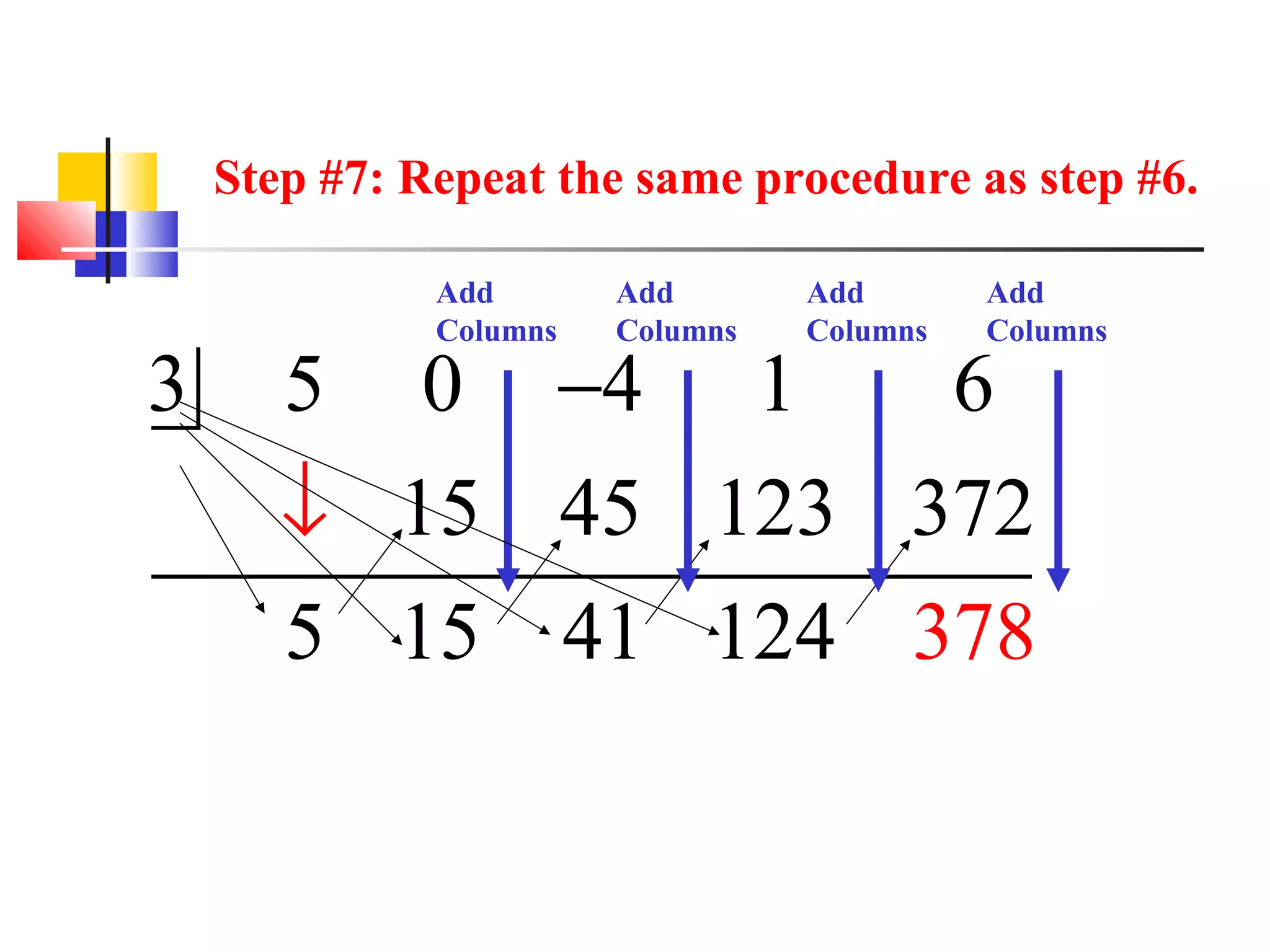
This document provides instructions for using synthetic division to divide polynomials. It contains the following key points: 1. Synthetic division can be used to divide polynomials when the divisor has a leading coefficient of 1 and there is a coefficient for every power of the variable in the numerator. 2. The procedure involves writing the terms of the numerator in descending order, bringing down the constant of the divisor, multiplying and adding down the columns to obtain the coefficients of the quotient polynomial and the remainder. 3. An example problem walks through each step of synthetic division to divide (5x^4 - 4x^2 + x + 6) / (x - 3), obtaining a quotient of 5x^3 + 15

2. Let’s look at how to do this
using the example:
( 5x
#1
4
− 4 x + x + 6 ) ÷ ( x − 3)
2
In order to use synthetic division these
two things must happen:
#2 The divisor must
There must be a
coefficient for
have a leading
every possible
coefficient of 1.
power of the
variable.

3. Step #1: Write the terms of the polynomial so
the degrees are in descending order.
5x + 0x − 4x + x + 6
4
3
2
Since the numerator does not contain all the powers of x,
you must include a 0 for the x 3 .

4. Step #2: Write the constant a of the divisor
x- a to the left and write down the
coefficients.
Since the divisor = x − 3, then a = 3
5x
4
0x
3
−4 x
2
+ x +6
↓
3
↓
↓
↓
↓
5
0
−4
1
6

5. Step #3: Bring down the first coefficient, 5.
3
5 0 −4 1 6
↓
5
Step #4: Multiply the first coefficient by r (3*5).
3
5
0
↓ 15
5
−4 1 6

6. Step #5: After multiplying in the diagonals,
add the column.
Add the
column
3
5 0 −4 1 6
↓ 15
5 15

7. Step #6: Multiply the sum, 15, by r; 15g
3=15,
and place this number under the next coefficient,
then add the column again.
3
Add
5 0 −4 1 6
↓ 15 45
5 15 41
Multiply the diagonals, add the columns.

8. Step #7: Repeat the same procedure as step #6.
3
5
Add
Columns
0
Add
Columns
−4
1
Add
Columns
Add
Columns
6
↓ 15 45 123 372
5 15 41 124 378

9. Step #8: Write the quotient.
The numbers along the bottom are
coefficients of the power of x in
descending order, starting with
the power that is one less than that
of the dividend.

10. The quotient is:
378
5x + 15x + 41x + 124 +
x−3
3
2
Remember to place the
remainder over the divisor.

11. Try this one:
1) (t 3 − 6t 2 + 1) ÷ ( t + 2)
−2
1 −6 0
1
−2 16 −32
1 −8 16 −31
31
Quotient = 1t − 8t + 16 −
t+2
2