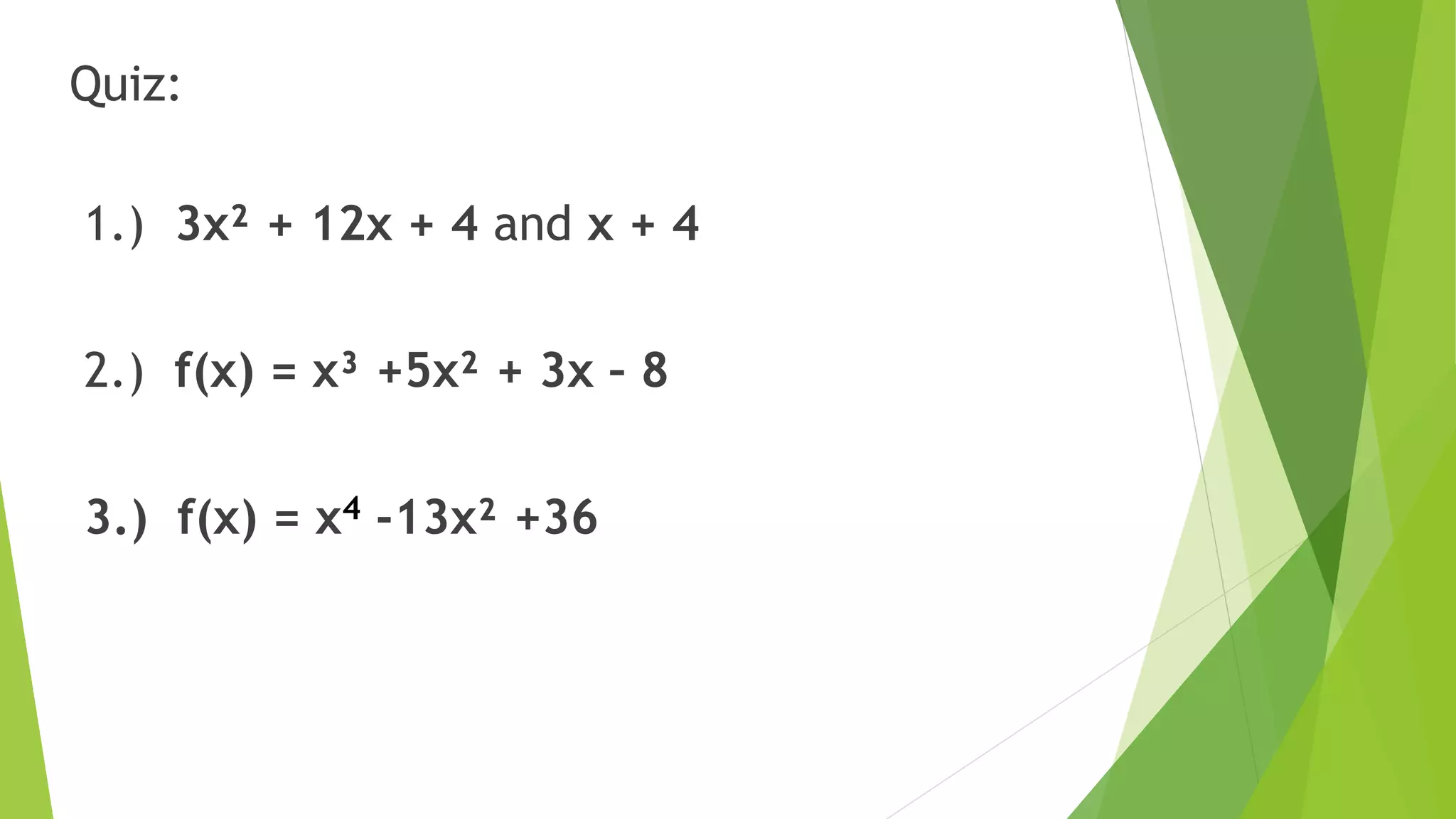This document discusses using synthetic division to find the quotient and remainder when dividing polynomials. It provides the step-by-step process for synthetic division, including examples of dividing polynomials where the divisor is of the form x + c and ax + c. The key steps are writing the coefficients of the dividend as the first row, taking the negative of the constant term of the divisor as the multiplier, bringing down terms and multiplying and adding sequentially until the last term. The numbers in the third row give the quotient polynomial. The document also discusses using factoring and setting each factor equal to 0 to find the zeros of a polynomial function.

1. Quotient of polynomial
Functions
(Synthetic Division)

2. STEPS FOR SYNTHETIC DIVISION METHOD (For divisor x + c)
 Write the numerical coefficients of the dividend in the 1st row.
 On one side of the first row, write the additive inverse of the constant of the divisor (c). This will serves as the
multiplier later.
 Bring down the first term on the third row.
 Multiply the value in step 3 by c. Write the product on the 2nd row of the next column.
 Add the result in step 4 with the number on the same column and write the sum on the 3rd row.
 Repeat steps 4 and 5 until the last coefficient, and until the bottom row is complete.
 The numbers on the third row serve as the numerical coefficient, of the quotient. To get the literal
coefficients, and their degree, just abstract one from the highest degree and affix them with the constant
arranged in descending order.

3. NOTE: For divisor(ax+ c), the same procedures are to beb
followed. But the multiplier will now be 𝑥 =
𝑐
𝑎
. After getting the
quotient, we divide the quotient by a, which is the numerical
coefficient of x in the divisor.

4. Examples:
Find the quotient when x³-9x²+23x-15 is divided by x-3.
Row 1 1 -9 23 -15 ˪𝟑
Row 2H3 -1815
_______________________
Row 3 1 -6 5 0
Therefore, the quotient is x²-6x-5.

5. Example:
Find the quotient when 3x⁴-4x³+11x²+7x-2 isdividedby3x+2.
Row 1 3-4117 -2 ˪ −
𝟐
𝟑
Row 2H-2 410 2
_____________________________
Row 3 3 -6 15-3 0
The quotient after performing synthetic division i 3x³-6²+15x-3. We
will divide this quotient by the numerical coefficient of x in the divisor
which is 3. Therefore, the final answer is x³-2x²+5x-1.

6. Example:3
Find the quotient when x³-4x²+5x+2 isdividedbyx+1
Row 1 1 -4 5 2˪ − 𝟏
Row 2H-1 5-10
__________________________
Row 3 1-510-8
Affixing all the literal coefficients, we can have x²-5x+10. Notice that after the
constant, 10, there is still another constant, -8. It only means that his value serves
as the remainder of the two polynomials after dividing. Therefore, we write the
quotient of the two polynomials as, x²-5x+10-
𝟖
𝒙+𝟏
.

7.  Reminder:
Steps in dividing polynomials with divisors x²+bx+c:
1.Write the coefficients of the divisor in Row 1.
2.Take the additive inverse of b and c, and write them on one side of
Row 1.
3.Bring down the first coefficient on Row 4.
4.Multiply the number in Row 4 to –b, then write the product on the
next column on Row 3, and to –c, then write the product on the next
column on Row 2.
5.Add the numbers in column 2 and write the sum in Row 4.
6.Repeat steps 4 and 5 until the last column.

8. Zeros of Polynomial
Functions
by Factor Theorem

9. In finding the zeros of polynomial functions, we are going to
apply the previous concepts learned, such as factoring, synthetic
division, and remainder theorem more specifically, if the given
polynomial is higher than second degree. Always take note that
the number of zeros of a polynomial depends on its degree. It
means, if the degree of the polynomial is 3, the number of
zeroes is also 3, and so on.

10. Example:
1. find the zeros of the polynomial function, f(x)= x³-x²-12x
f(x)=x³-x²-12x
=x³-x²-12x = 0
=x(x²-x-12)= 0
=x(x-4)(x+3)=0
x= 0 x-4 = 0 x+3 = 0
x= 4 x= -3

11. Checking: f(x)=x³-x²-12x
f(0)= (0)³-(0)²-12(0) f(-3)= (-3)³-(-3)²-12(-3)
= 0 = -27- 9 + 36
= -36 + 36
= 0
f(4) = (4)³-(4)²-12(4)
= 64- 16- 48
= 64 – 64
= 0
Therefore, we can say that the zeros of the polynomial function, f(x)= x³-x²-
12 are 0, 0 and 0.

12. Zeros of Polynomial Functions
by Synthetic division

13. Example:
1.Find the zeros of the polynomial function, f(x)= x4 +5x³+5x²-5x-6.
P= ±1, ±2, ±3, ±6 1 5 5 -5 -6 L 1
q= ±1 1 6 11 6
p 1 6 11 6 0
q = ±1, ±2, ±3, ±6
1 6 11 6 L-1
-1 -5 -6
1 5 6 0

14. x² + 5x + 6 = 0
(x + 3) (x + 2) = 0
x+3 = 0 x + 2 = 0
x = -3 x = -2
Therefore, the zeros are 1, -1, -2, and -3

15. Quiz:
1.) 3x² + 12x + 4 and x + 4
2.) f(x) = x³ +5x² + 3x – 8
3.) f(x) = x4 -13x² +36