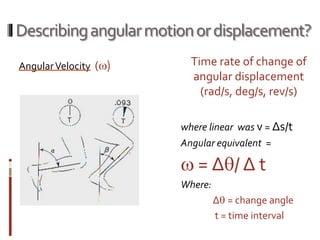
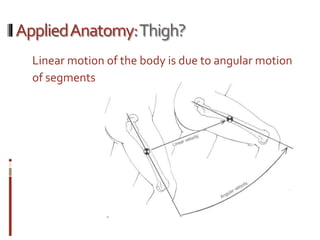
This document defines and provides equations for angular distance, velocity, and acceleration. It explains that angular distance is equal to the angular path length. Angular velocity is the rate of change of angular displacement with respect to time. Angular acceleration is the rate of change of angular velocity with respect to time. Linear velocity at a point can be calculated as the sum of angular velocity times the radius of rotation and any linear velocity of the body.

2. Describingangularmotionordisplacement?
Angular Distance and Displacement
 = angle
Units of measurement
• radians (1 rad = 57.3)
• degree ()
• revolutions (revs)

3. Describingangularmotionordisplacement?
AngularVelocity () Time rate of change of
angular displacement
(rad/s, deg/s, rev/s)
where linear was v = Δs/t
Angular equivalent =
 = Δ/ Δ t
Where:
Δ = change angle
t = time interval

4. Describingangularmotionordisplacement?
Angular Acceleration () Time rate of change of
angular velocity(rad/s/s,
deg/s/s, rev/s/s)
Where linear was a = Δv/t
Angular equivalent =
 = Δ /t
Δ  = change angular velocity
t = time interval

5. CombiningLinearandAngularVelocity?
LinearVelocity Endpoint =
AngularVelocity () x Radius of Rotation (r)
You MUST only work in
radians when using this
formula
to convert
•  degrees/ 57.3
Lv = xr

6. RadiusofRotation?:Golf
LinearVelocity ofVb (end of club)
is greater thanVa (for same )
Linxr
Lin
r is larger inVb so club head
linear velocity is 
When a rotating body moves from one position to another, the
angular distance through which it moves is equal to the length of the
angular path.
Vb
Va

7. AppliedAnatomy:Thigh?
Linear motion of the body is due to angular motion
of segments

8. Cricket?
In situations where the objects ‘s COM has a linear
velocity it must be added to the equation.
Kicking
vball = vhip + (xr)
Bowling (throwing)
vball = vshoulder + (xr)
Where the shoulder in throwing and the hip in kicking already incorporates
the linear velocity of the COM

9. Question
Calculate the linear velocity of the throwing-shoulder at release of a discus
thrower , who:
1. Moves across the circle at 1 m/s
2. Rotates the trunk through 360 degrees in 0.2 s
3. The length from the central axis of trunk rotation to the shoulder is
0.25 m

11. LectureOutcomes
• What is the equation for calculating angular velocity? Write as an
equation and as a definition.
• Write the equation for the velocity of the ankle joint in a soccer kick
or a netball shot for goal (start the kick at the ankle, which has a
velocity of 2 ms-1 and the netball shot at the shoulder which has
the same velocity).
• Define the angular equivalent of displacement, velocity and
acceleration using formula and words.

13. RealWorldProblem
A softballer rotates the bat horizontally at 10 rad/s. If her shoulder is
moving forward at 2m/s and the distance of the point of impact with
the ball and her shoulder is 1m, what is the forward velocity of the end
of the bat at the point of impact?

15. RealWorldProblem
A softballer rotates the bat horizontally at 10 rad/s. If her
shoulder is moving forward at 2m/s and the distance of the
point of impact with the ball and her shoulder is 1m, what is the
forward velocity of the end of the bat at the point of impact?
vbat = vshoulder + (xr)
vbat = 2+ (10x1)
12 m/s

16. Answers
1. Convert degrees to radians
= 360/ 57.3
= 6.28 radians
2. Calculate angular velocity
ω = /t
= 6.28/ 0.2
= 31.4 rad/s
3.Vshoulder =Vcg + (trunk x ltrunk)
= Vcg + (31.4) x (0.25)
= 1 + 7.85 m/s = 8.85 m/s