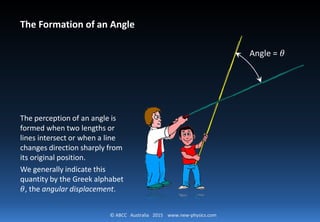
The document discusses the definition and formation of angles, indicating that an angle is created when two lines intersect. It explains how angles are measured in degrees and radians, detailing the conversion between the two systems. Additionally, it presents typical angles and their circular equivalents.

1. © ABCC Australia 2015 www.new-physics.com
ANGLES & MEASUREMENT
PM [B05]

2. © ABCC Australia 2015 www.new-physics.com
The Formation of an Angle
The perception of an angle is
formed when two lengths or
lines intersect or when a line
changes direction sharply from
its original position.
We generally indicate this
quantity by the Greek alphabet
𝜃𝜃, the angular displacement.
Angle = 𝜃𝜃

3. © ABCC Australia 2015 www.new-physics.com
Definition of the Angle
The word angle comes from the
Latin word angulus which means
"a corner".
An angle is not the space
between the two side lengths
but the corner that makes it up.
Space is a derived quantity, but
angle is a primary one. It cannot
be derived from more basic
units.
s (arc)
𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴
r (radius)
c (circumference)
0 (center or
origin)

4. © ABCC Australia 2015 www.new-physics.com
Measuring Angles in
Degrees
The earliest angle
measurements were counted in
degrees.
A degree (°) is the angle
subtended by an arc of a circle
equal to 1/360 of the
circumference of the circle.
Thus there are 360 degrees if
the vector is fully extended
round a circle.
A minute (') is 1/60 of a degree
and a second (") is 1/60 of a
minute, just like the minute
division on a clock face.
θ° (angle) =45°
𝜃𝜃𝜃

5. © ABCC Australia 2015 www.new-physics.com
Angles in Radians
However for the study of circular
motion it is more convenient to
employ circular measure in
radians.
A radian is the angle subtended at
the center of a circle by an arc
equal to the radius (𝑟𝑟) of the
circle.
𝜃𝜃
𝑟𝑟
𝑟𝑟

6. © ABCC Australia 2015 www.new-physics.com
Unit Radian
Although the radian is also an
angular measurement like the
degree units (°), there is no
traditional symbol to it except
the word ‘rad’.
To rank it in the same standing
as the degree (°) in angular
measure, we propose to denote
the radian unit (rad) ‘at times’
by the symbol 𝜃𝜃𝑟𝑟𝑟𝑟𝑟𝑟
or 𝜃𝜃𝑐𝑐
in
circular measure.
1 radian is written as 1𝑟𝑟𝑟𝑟𝑟𝑟 or 1𝑐𝑐.
𝜃𝜃 remains the common symbol
for both measuring systems.
𝜃𝜃
𝑎𝑎𝑎𝑎𝑎𝑎 = 𝑟𝑟
𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟 = 𝑟𝑟

7. © ABCC Australia 2015 www.new-physics.com
Converting Angles
It is easy to convert between
degree measurement and radian
measurement.
The circumference of the entire
circle is 2𝜋𝜋 (𝜋𝜋 is about 3.14159),
so it follows that 360° equals 2𝜋𝜋
radians.
Hence, 1° equals 2𝜋𝜋/360
radians, and 1 radian equals
360/2𝜋𝜋 degrees.
Some of the typical angles are
written with their circular
equivalents as:
• 1rad = 360˚/2π = 57.3˚
•
𝜋𝜋rad
2
= 90˚
• 𝜋𝜋rad = 180˚
•
3
2
𝜋𝜋rad = 270˚
• 2𝜋𝜋rad = 360˚

8. © ABCC Australia 2015 www.new-physics.com
COMPLEX POLAR COORDINATES
To be carried on PM [BO6]:
ABCC