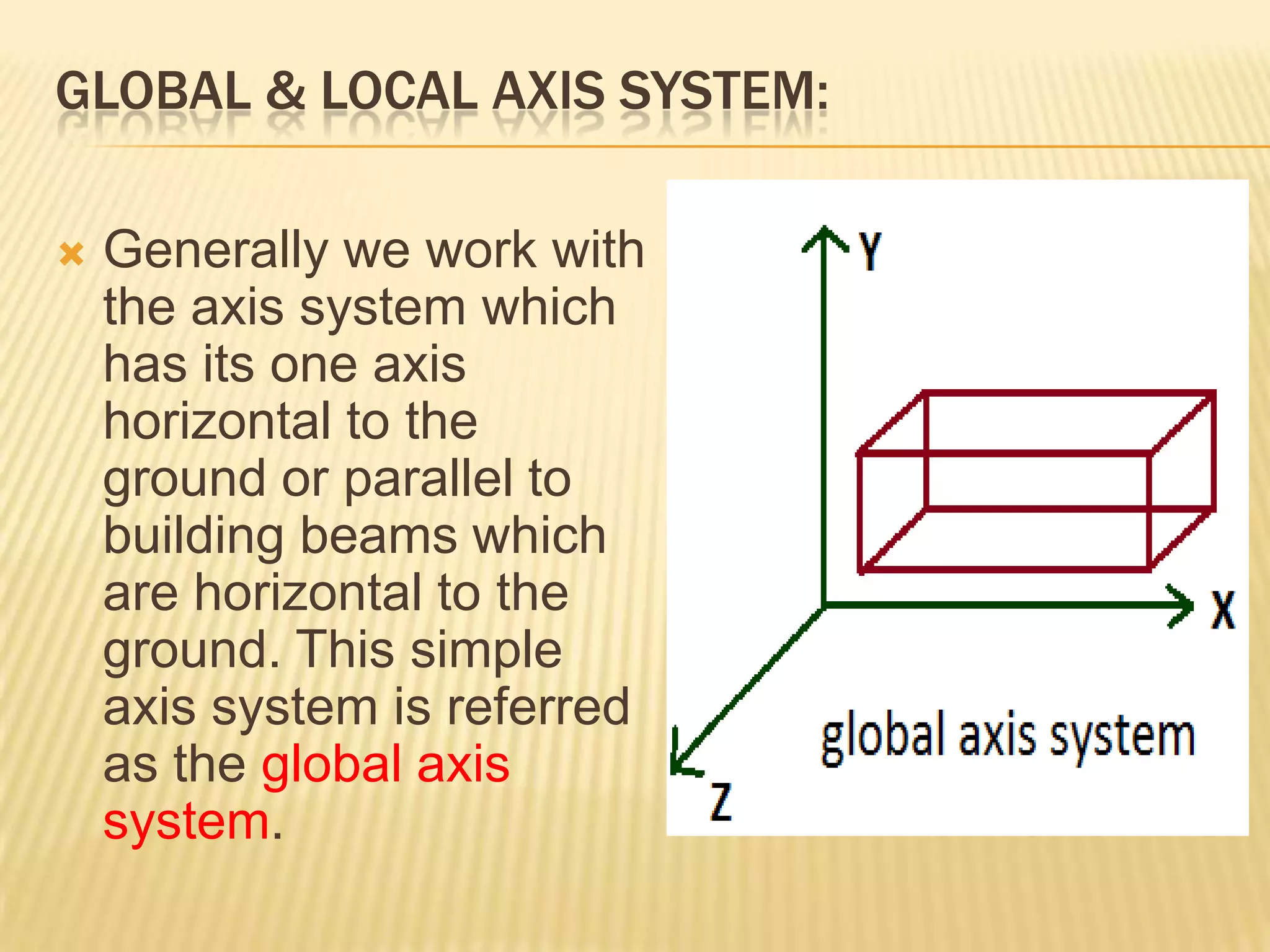
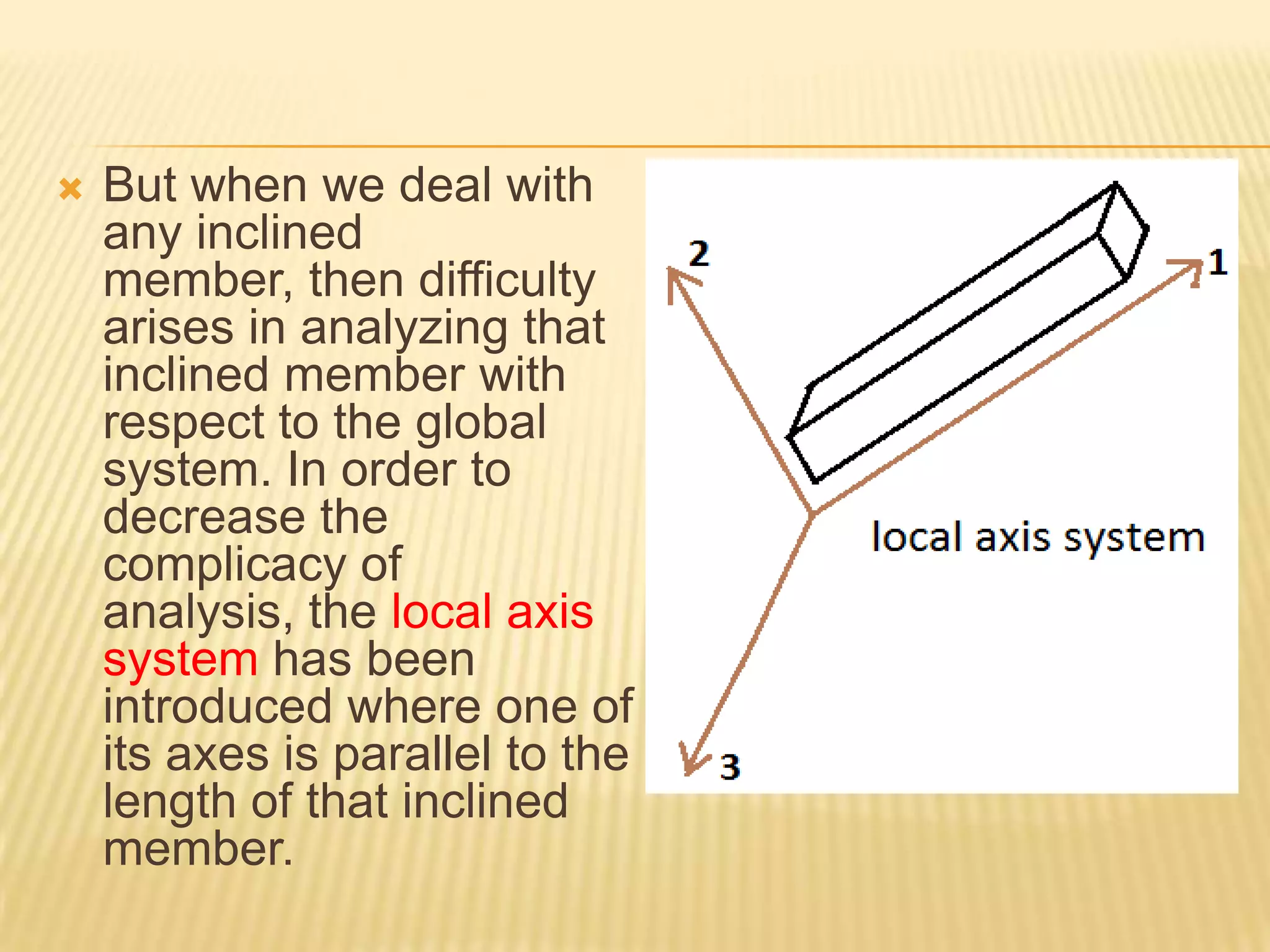
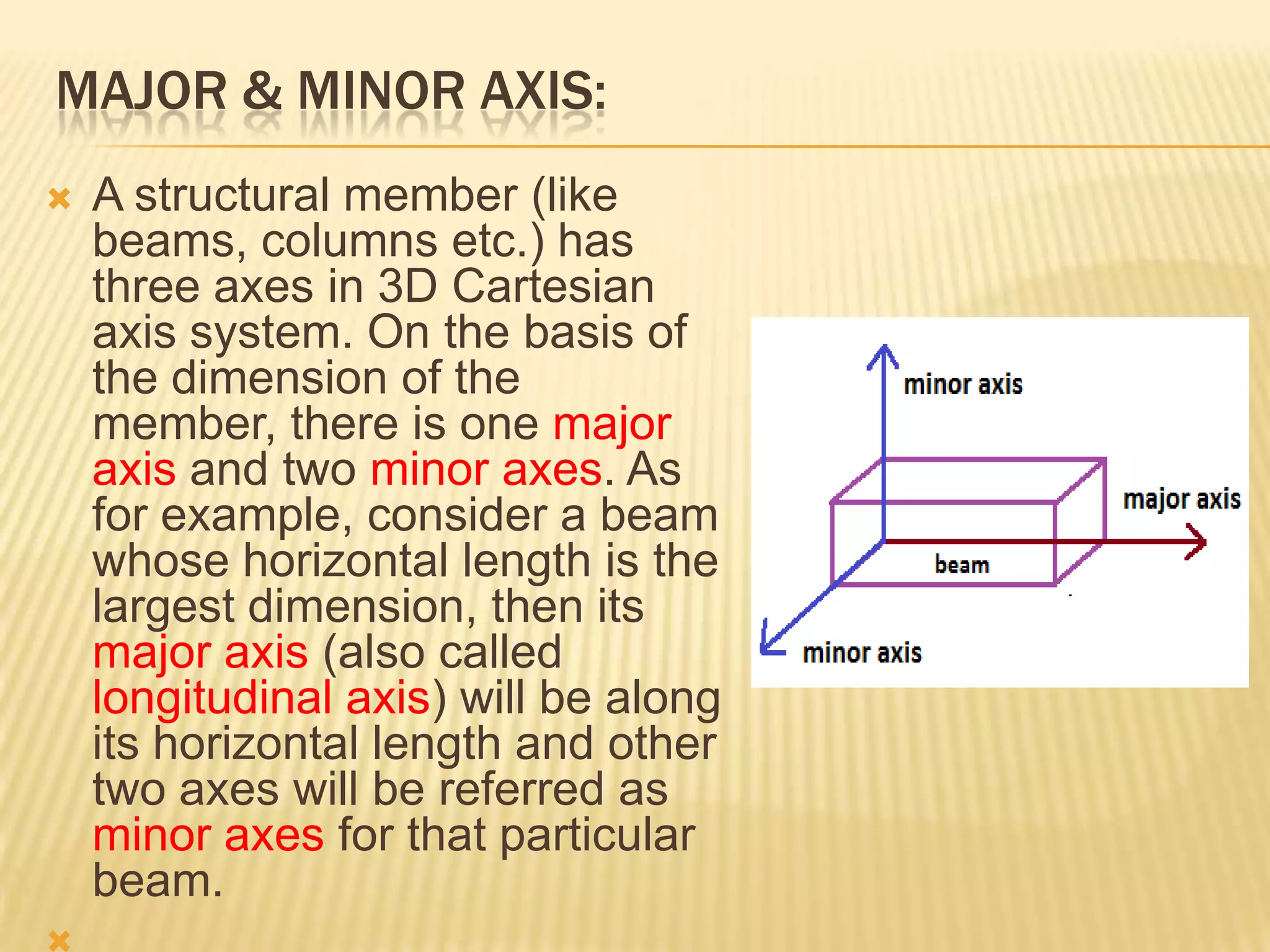
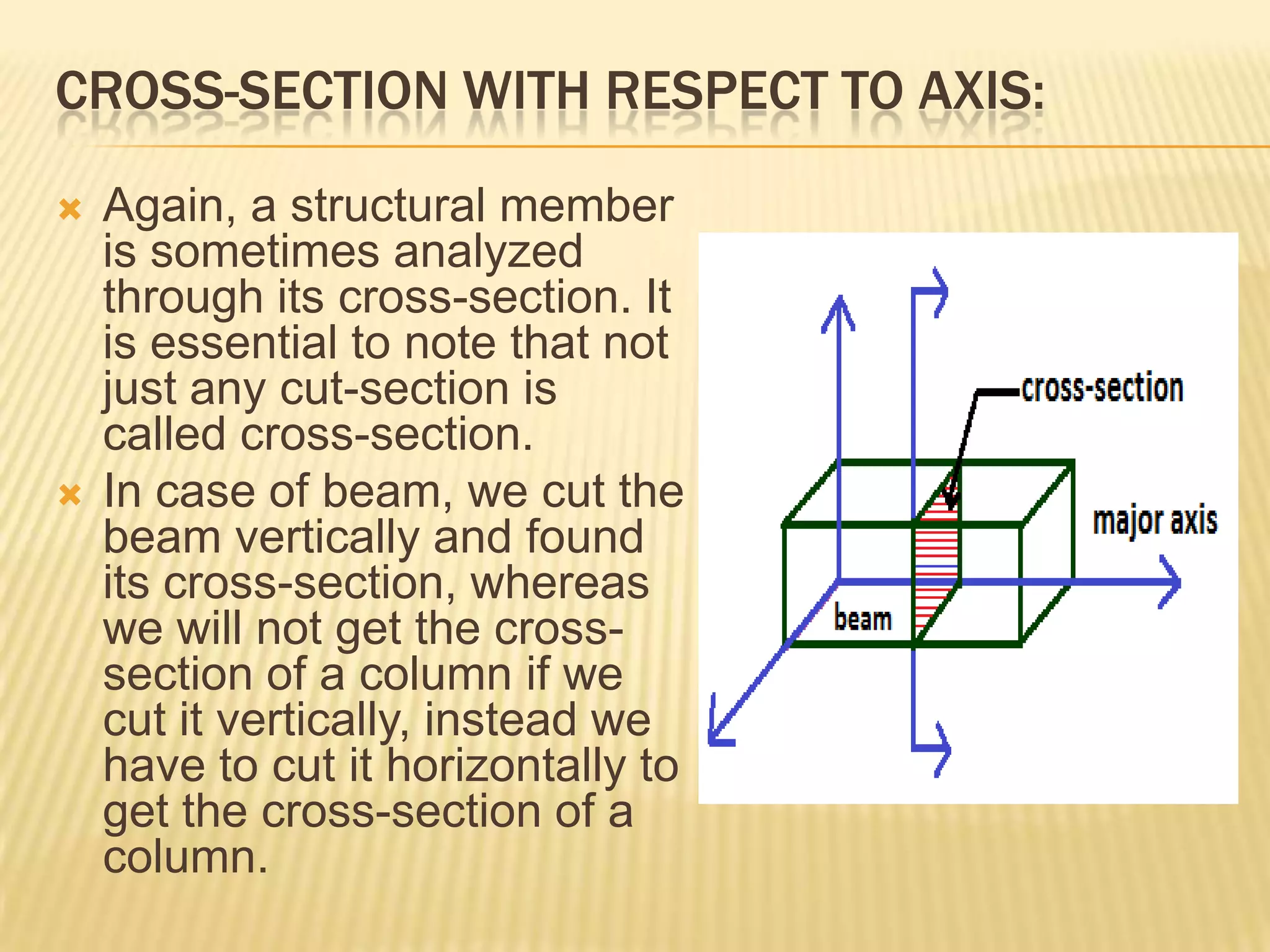
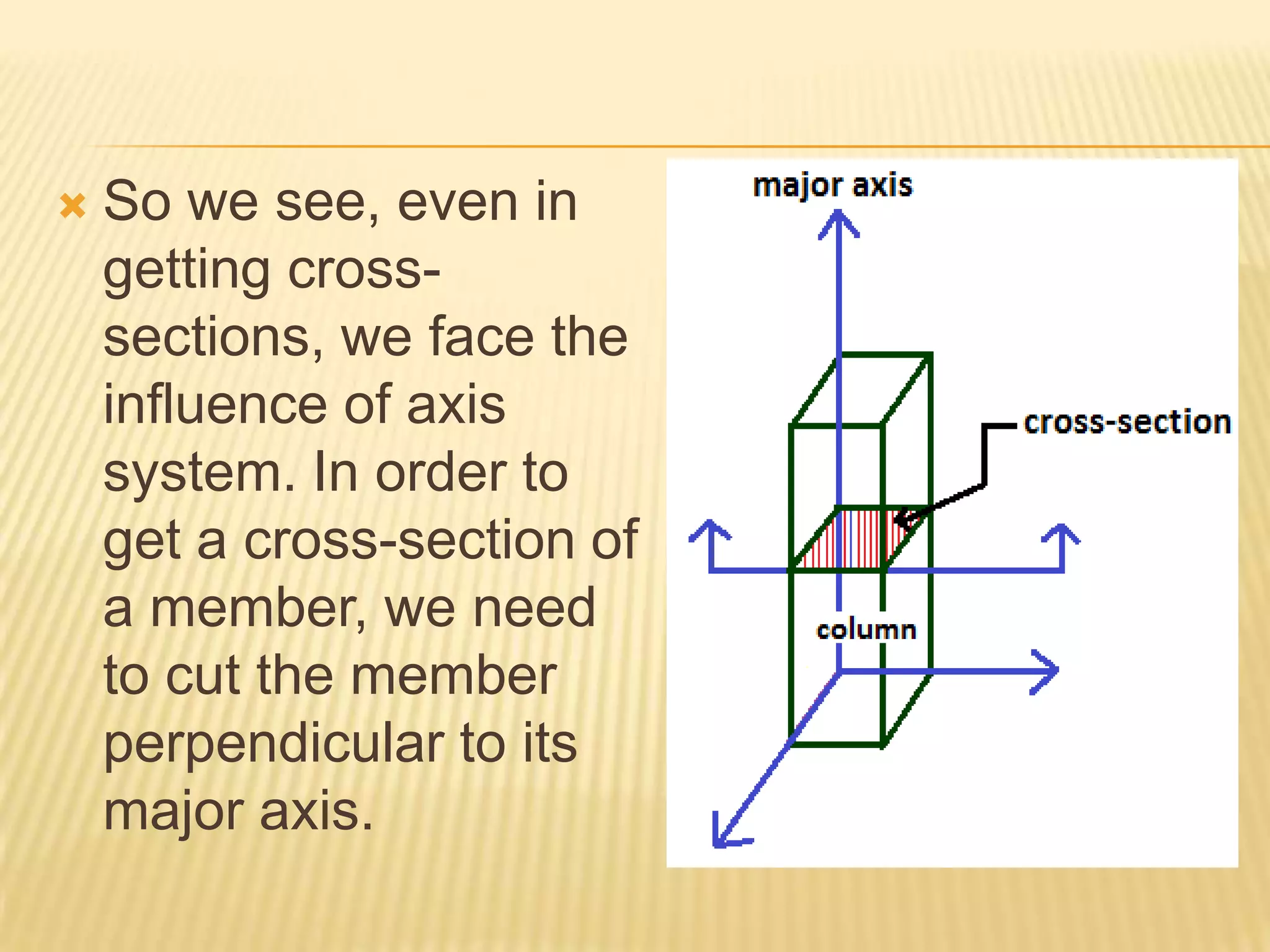
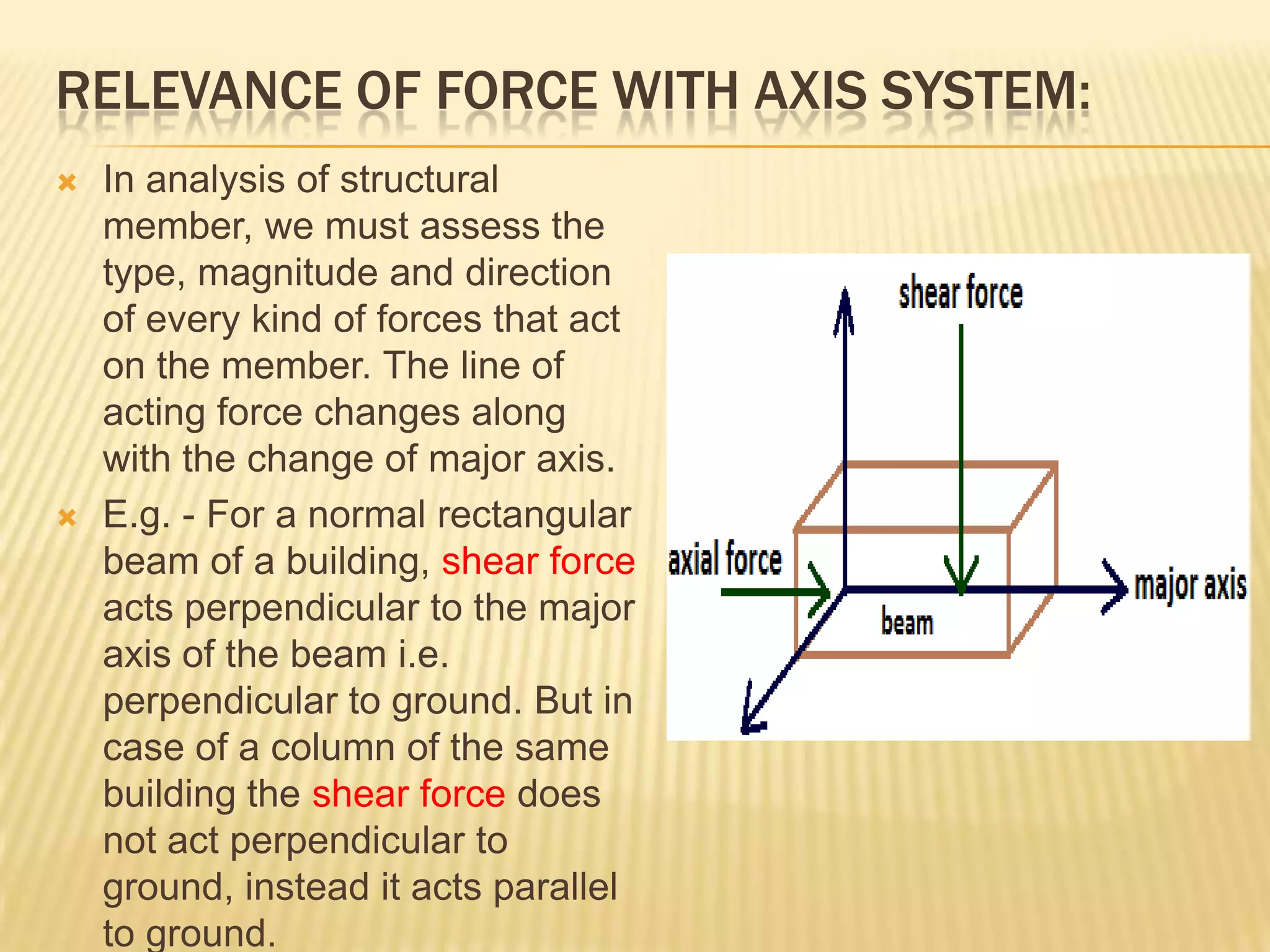
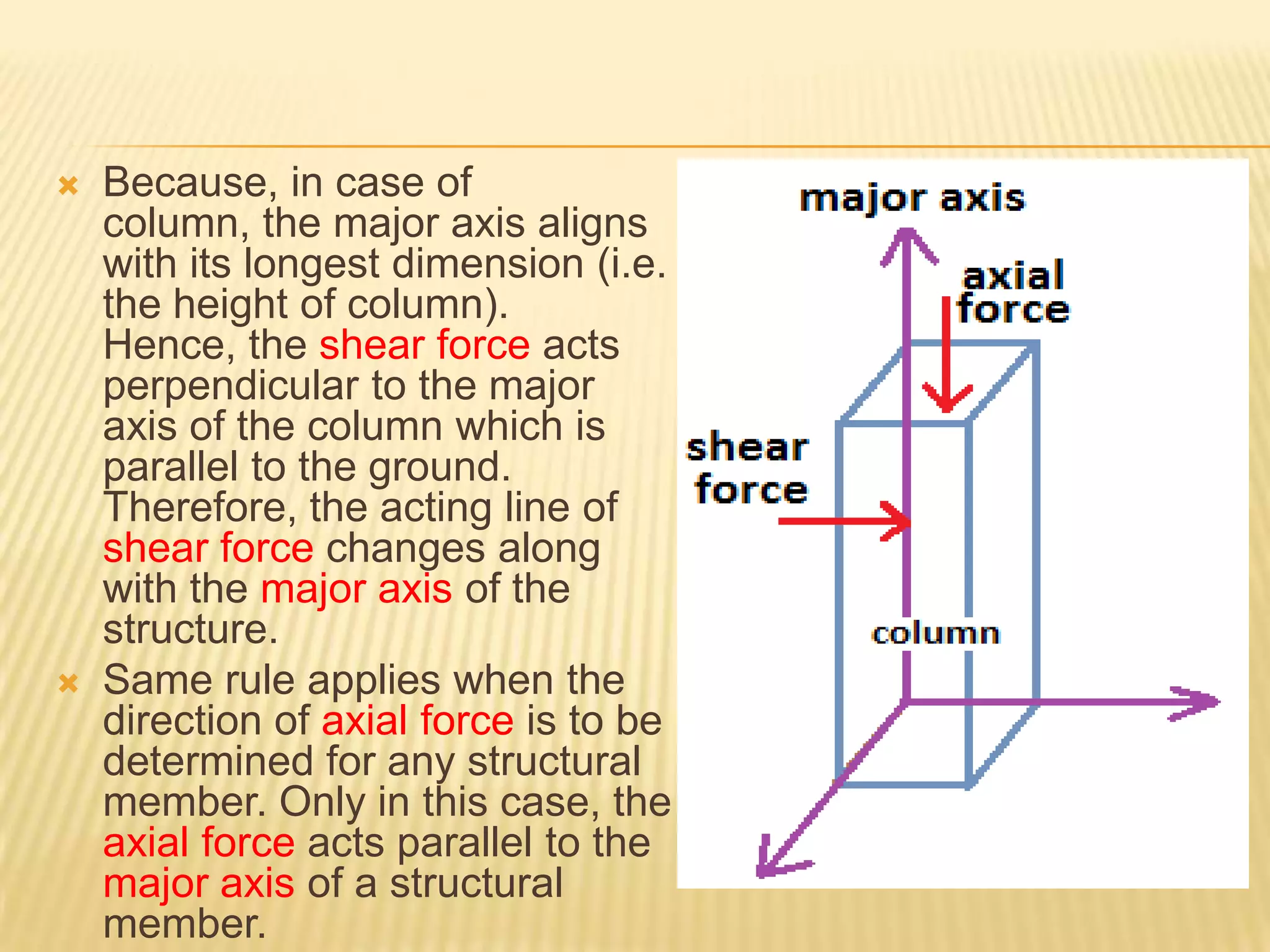
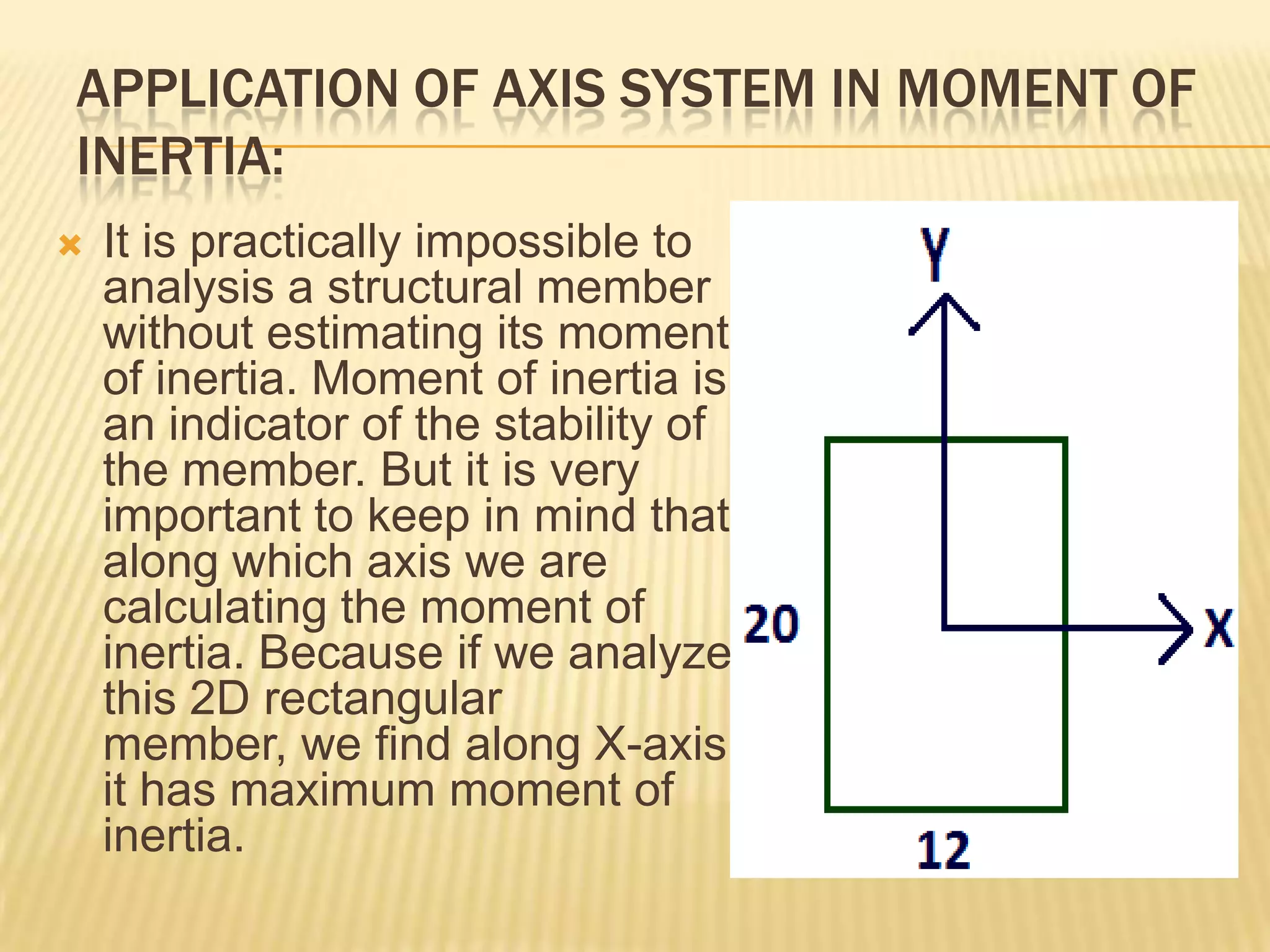
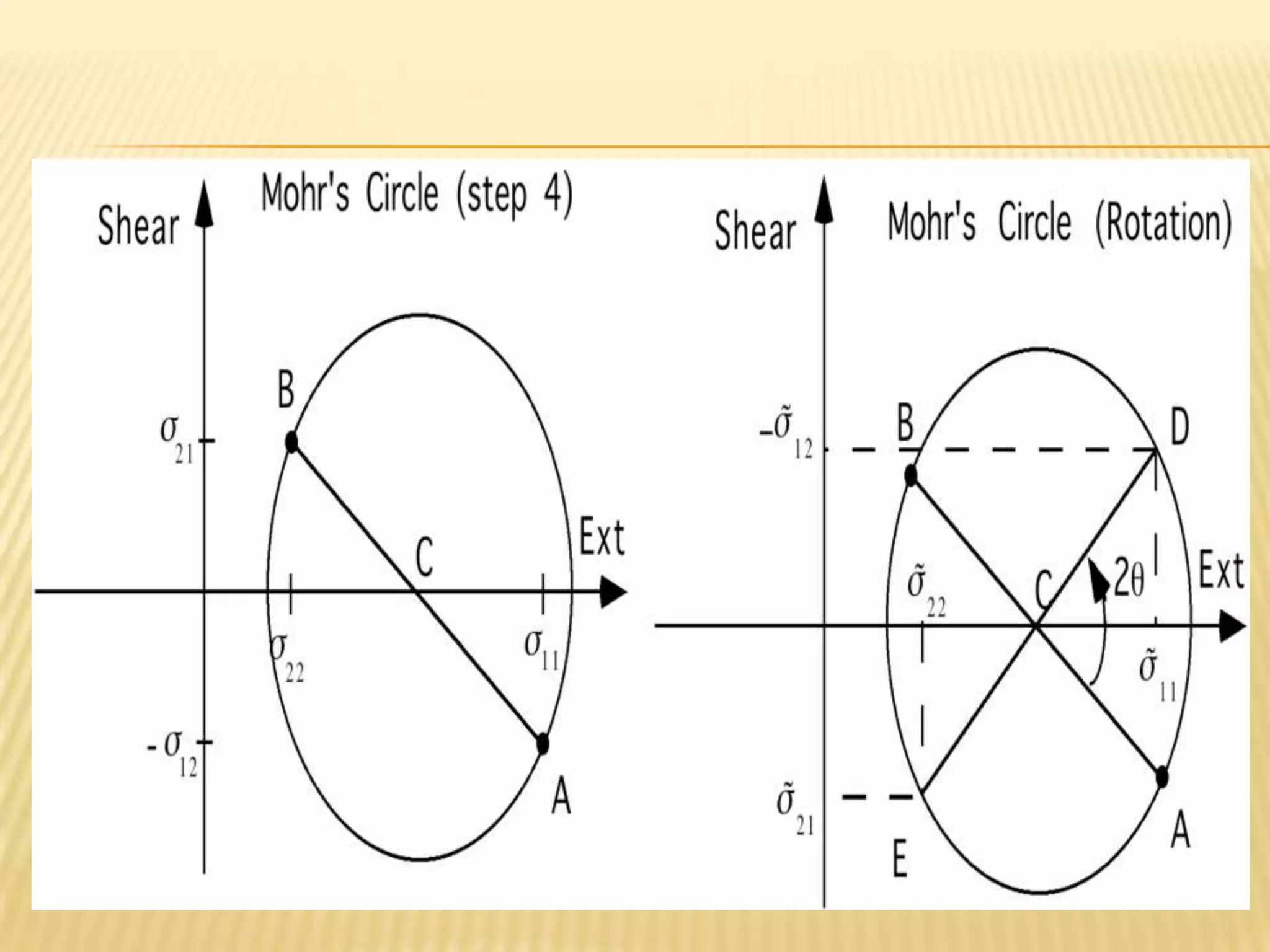
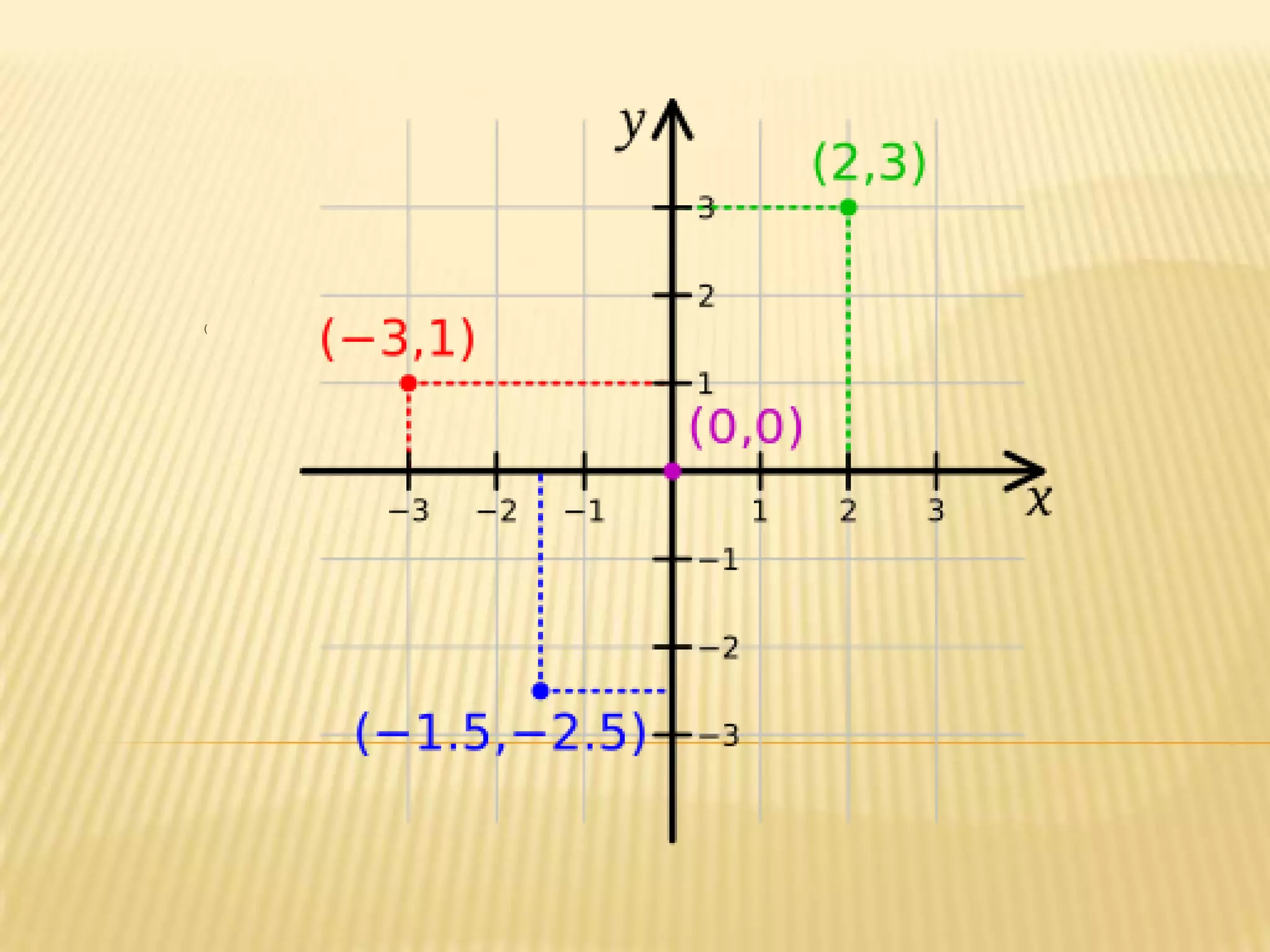
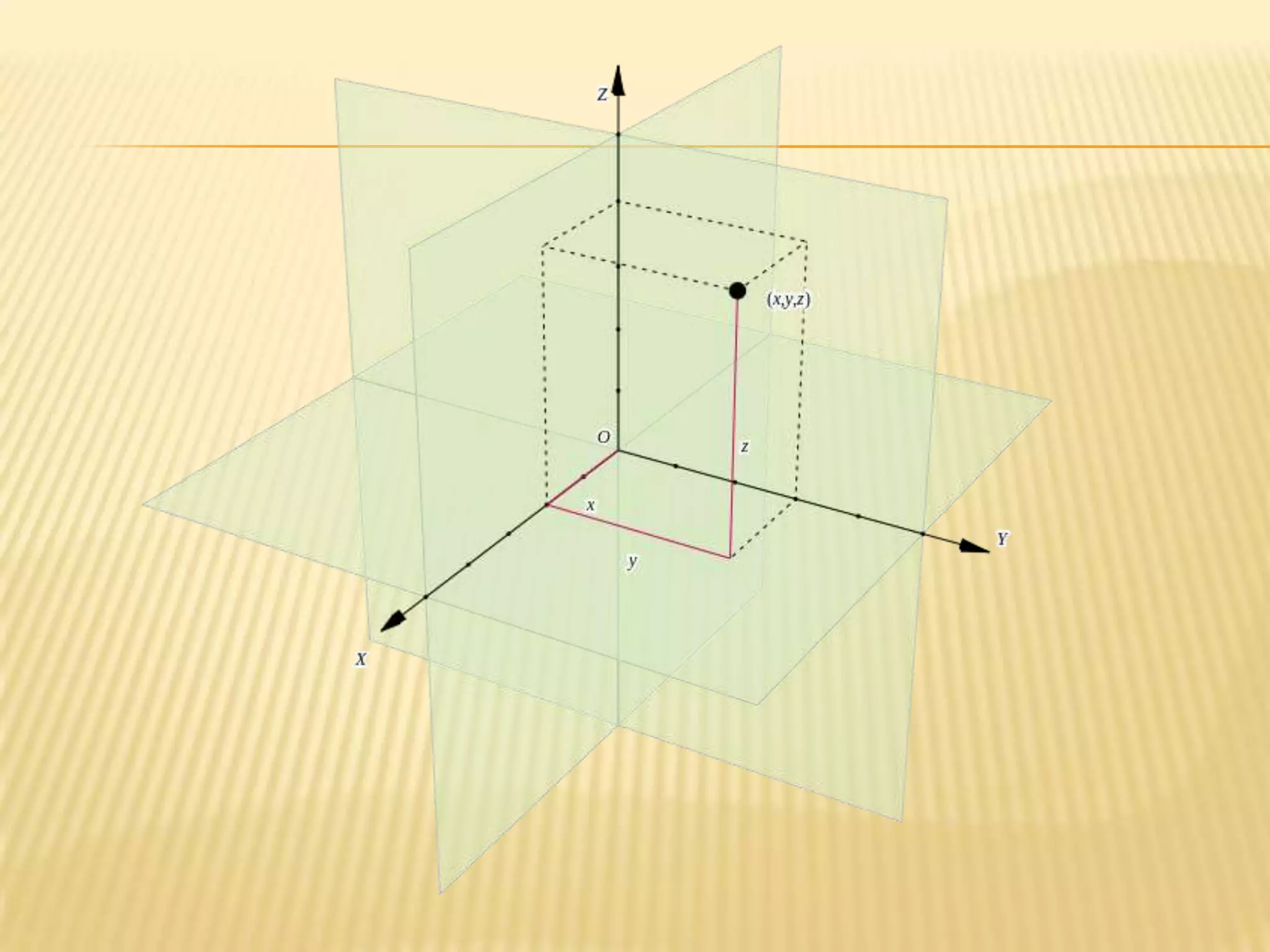
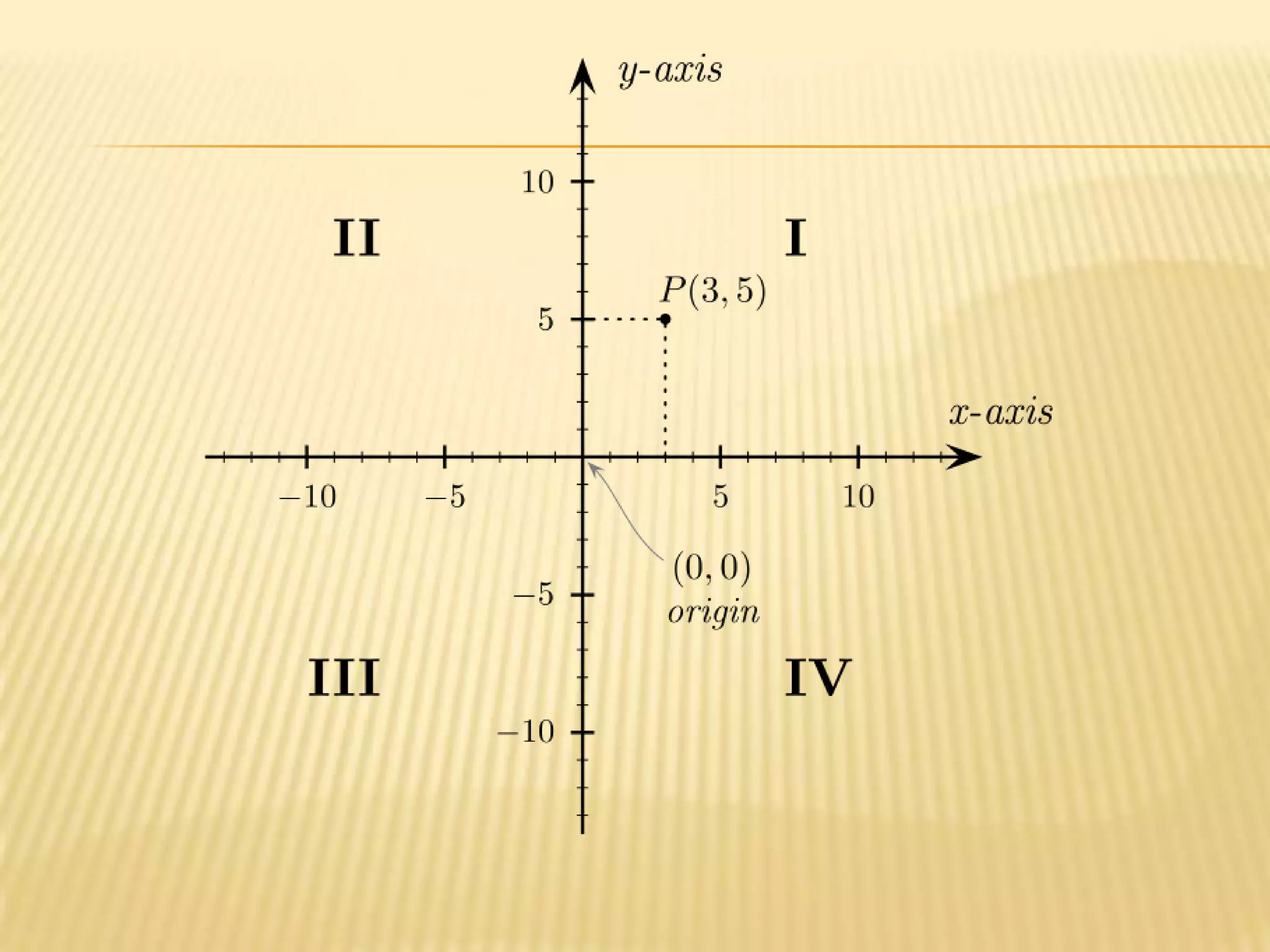
This document provides information about axis systems that are important in civil engineering. It discusses how global and local axis systems are used to analyze structural members. A major axis is defined as being parallel to the longest dimension of a member, while minor axes are perpendicular to the major axis. Cross-sections are defined as cuts perpendicular to the major axis. Forces like shear and axial forces are determined based on their direction relative to the major axis. Moment of inertia calculations depend on the axis used. Mohr's circle, which relates stresses, also relies on defining an axis system. Axis systems are thus a fundamental concept in engineering mechanics and the analysis of structures.

1. AHSANULLAH UNIVERSITY OF SCIENCE &
TECHNOLOGY
CE-416
PRE-STRESSED CONCRETE SESSIONAL
PRESENTATION ON “AXIS SYSTEM”
Submitted by
Faria Haider
10.01.03.057

2. AXIS SYSTEM





An axis is a straight line, sometimes seen, sometimes not, that is
important in mathematics, art, science and our survival. The most
famous axis is the one the earth spins around, giving us the 24hour day.
This task explains how to define a new three-axis system locally.
There are two ways of defining it: either by selecting geometry or
by entering coordinates.
The definition of an axis is a real or imaginary line on which
something rotates, or a straight line around which things are
evenly arranged.
An example of axis is an imaginary line running through the earth
on which the earth rotates.
An example of axis is the line running through the body from head
to feet determining left and right sides.

3. CARTESIAN COORDINATE SYSTEM
A Cartesian coordinate system is a coordinate
system that specifies each point uniquely in a plane by
a pair of numerical coordinates, which are the signed
distances from the point to two fixed perpendicular
directed lines, measured in the same unit of length.
Each reference line is called a coordinate axis or just
axis of the system, and the point where they meet is its
origin, usually at ordered pair (0, The coordinates
0).
can also be defined as the positions of the
perpendicular projections of the point onto the two
axes, expressed as signed distances from the origin.

4. (

5. Cartesian coordinates are the foundation of
analytic geometry, and provide enlightening
geometric interpretations for many other
branches of mathematics, such as linear
algebra, complex analysis, differential
geometry, multivariate calculus, group
theory, and more. A familiar example is the
concept of the graph of a function. Cartesian
coordinates are also essential tools for most
applied disciplines that deal with
geometry, including
astronomy, physics, engineering, and many
more. They are the most common coordinate
system used in computer graphics, computeraided geometric design, and other geometryrelated data processing.

6. CARTESIAN COORDINATES IN TWO
DIMENSIONS

The modern Cartesian coordinate system in two
dimensions (also called a rectangular coordinate
system) is defined by an ordered pair of
perpendicular lines (axes), a single unit of length
for both axes, and an orientation for each axis.
(Early systems allowed "oblique" axes, that is, axes
that did not meet at right angles.) The lines are
commonly referred to as the x and y-axes where
the x-axis is taken to be horizontal and the y-axis
is taken to be vertical. The point where the axes
meet is taken as the origin for both.

8. CARTESIAN COORDINATES IN THREE
DIMENSIONS

Choosing a Cartesian coordinate system for a
three-dimensional space means choosing an
ordered triplet of lines (axes), any two of them
being perpendicular; a single unit of length for all
three axes; and an orientation for each axis. As
in the two-dimensional case, each axis becomes
a number line. The coordinates of a point p are
obtained by drawing a line through p
perpendicular to each coordinate axis, and
reading the points where these lines meet the
axes as three numbers of these number lines.

10. QUADRANTS AND OCTANTS


The axes of a two-dimensional Cartesian system divide the
plane into four infinite regions, called quadrants, each
bounded by two half-axes. These are often numbered from
1st to 4th and denoted by Roman numerals: I (where the
signs of the two coordinates are I (+,+), II (−,+), III (−,−), and
IV (+,−). When the axes are drawn according to the
mathematical custom, the numbering goes counterclockwise starting from the upper right ("northeast")
quadrant.
Similarly, a three-dimensional Cartesian system defines a
division of space into eight regions or octants, according to
the signs of the coordinates of the points. The convention
used for naming a specific octant is to list its signs, e.g. (+ +
+) or ( - + -). The n-dimensional generalization of the
quadrant and octant is the orthant, and the same naming
system applies.

12. CARTESIAN FORMULAS FOR THE PLANE

Distance between two points

The Euclidean distance between two points of the plane with Cartesian
coordinates
and
is

This is the Cartesian version of Pythagoras' theorem. In threedimensional space, the distance between points
and
is

Which can be obtained by two consecutive applications of Pythagoras’
theorem.

13. POLAR COORDINATE SYSTEM
In mathematics, the polar coordinate
system is a two-dimensional coordinate
system in which each point on a plane is
determined by a distance from a fixed point
and an angle from a fixed direction.
 The fixed point (analogous to the origin of a
Cartesian system) is called the pole, and the
ray from the pole in the fixed direction is the
polar axis. The distance from the pole is
called the radial coordinate or radius, and the
angle is the angular coordinate, polar angle.


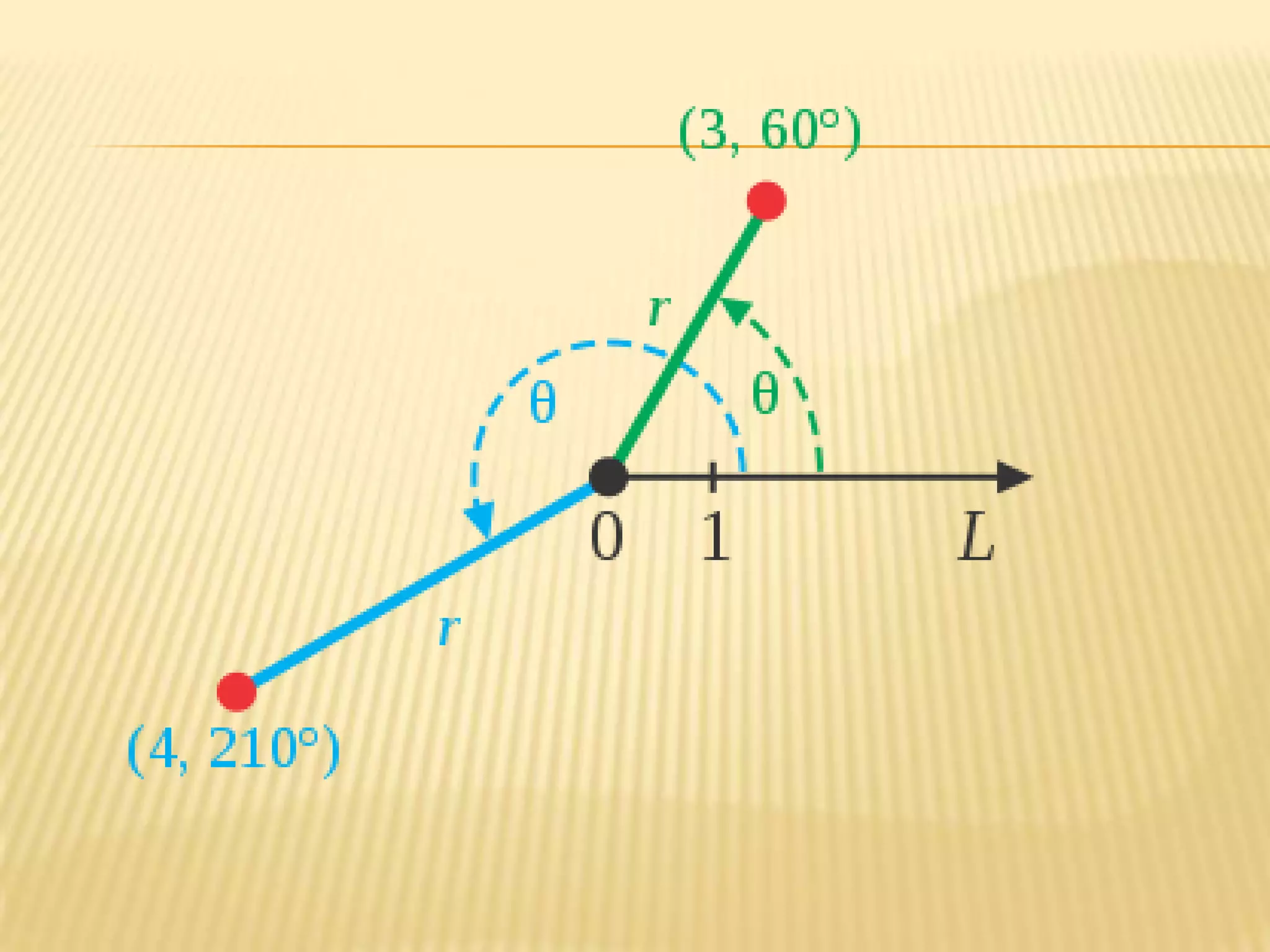
15. CONVERTING BETWEEN POLAR AND
CARTESIAN COORDINATES

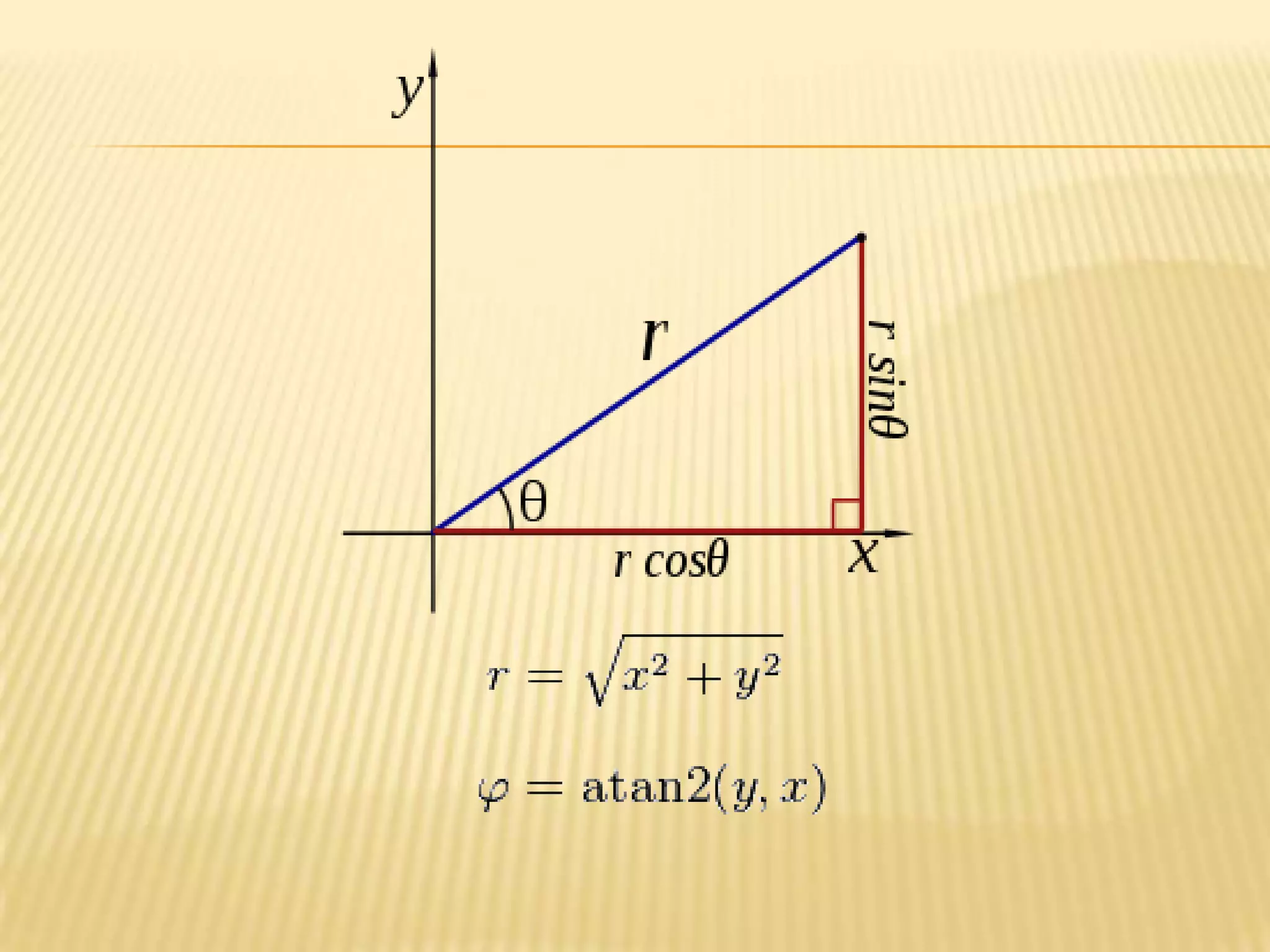
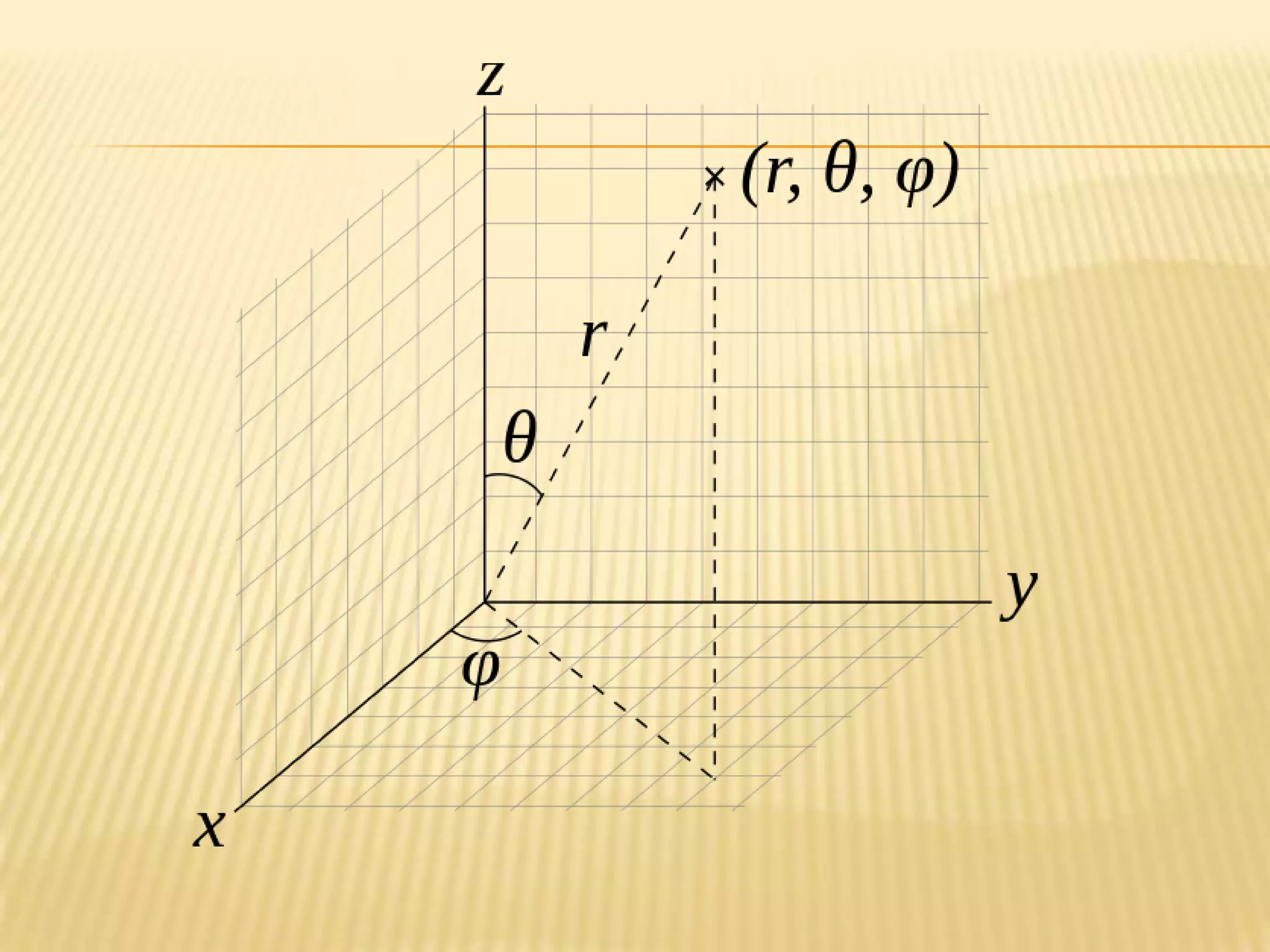
The polar coordinates r and φ can be converted
to the Cartesian coordinates x and y by using
the trigonometric functions sine and cosine:
The Cartesian coordinates x and y can be
converted to polar coordinates r and φ with
r ≥ 0 and φ in the interval (−π, π] by:

17. SPHERICAL COORDINATE SYSTEM


In mathematics, a spherical coordinate system is a
coordinate system for three-dimensional space where
the position of a point is specified by three numbers:
the radial distance of that point from a fixed
origin, its polar angle measured from a fixed zenith
direction, and the azimuth angle of its orthogonal
projection on a reference plane that passes through
the origin and is orthogonal to the zenith, measured
from a fixed reference direction on that plane.
The radial distance is also called the radius or radial
coordinate. The polar angle may be called
colatitude, zenith angle, normal angle, or
inclination angle.

18. 
The use of symbols and the order of the
coordinates differs between sources. In one
system frequently encountered in physics
(r, θ, φ) gives the radial distance, polar
angle, and azimuthal angle, whereas in
another system used in many mathematics
books (r, θ, φ) gives the radial
distance, azimuthal angle, and polar angle. In
both systems ρ is often used instead of r.
Other conventions are also used, so great
care needs to be taken to check which one is
being used.

20. CYLINDRICAL COORDINATE SYSTEM



A cylindrical coordinate system is a three-dimensional
coordinate system that specifies point positions by the
distance from a chosen reference axis, the direction from
the axis relative to a chosen reference direction, and the
distance from a chosen reference plane perpendicular to
the axis. The latter distance is given as a positive or
negative number depending on which side of the
reference plane faces the point.
The origin of the system is the point where all three
coordinates can be given as zero. This is the intersection
between the reference plane and the axis.
The axis is variously called the cylindrical or longitudinal
axis, to differentiate it from the polar axis, which is the
ray that lies in the reference plane, starting at the origin
and pointing in the reference direction.

22. BIPOLAR CYLINDRICAL COORDINATES

The term "bipolar" is often used to describe other
curves having two singular points (foci), such as
ellipses, hyperbolas, and Cassini ovals.
However, the term bipolar coordinates is never
used to describe coordinates associated with
those curves, e.g., elliptic coordinates. The classic
applications of bipolar coordinates are in solving
partial differential equations, e.g., Laplace's
equation or the Helmholtz equation, for which
bipolar coordinates allow a separation of variables.
A typical example would be the electric field
surrounding two parallel cylindrical conductors.

24. AXIS SYSTEM IN CIVIL ENGINEERING




Axis system exists in almost every sphere of
universe.
It has its massive usage in the field of cosmic
system, medical fraternity , music world, data
processing & communication system, mathematics
& as well as in every engineering sector.
Axis system has its wings stretched in every little
aspect of civil engineering chapters. As for
example, in engineering
mechanics, hydraulics, centroid, force
system, moment of inertia and so on.
The importance of axis system in civil engineering
can be demonstrated briefly in following slides.

25. IMPORTANCE OF AXIS SYSTEM IN
CIVIL ENGINEERING:

In a sense, axis system is stitched with the
base of civil engineering mechanics. Civil
engineers deal with frequent analysis &
design which involves every kind of
forces, stresses and their projections, which
includes the application if axis system. Some
basic but very important phases of
application of axis system are described in
the following slides-

26. GLOBAL & LOCAL AXIS SYSTEM:

Generally we work with
the axis system which
has its one axis
horizontal to the
ground or parallel to
building beams which
are horizontal to the
ground. This simple
axis system is referred
as the global axis
system.

27. 
But when we deal with
any inclined
member, then difficulty
arises in analyzing that
inclined member with
respect to the global
system. In order to
decrease the
complicacy of
analysis, the local axis
system has been
introduced where one of
its axes is parallel to the
length of that inclined
member.

28. MAJOR & MINOR AXIS:

A structural member (like
beams, columns etc.) has
three axes in 3D Cartesian
axis system. On the basis of
the dimension of the
member, there is one major
axis and two minor axes. As
for example, consider a beam
whose horizontal length is the
largest dimension, then its
major axis (also called
longitudinal axis) will be along
its horizontal length and other
two axes will be referred as
minor axes for that particular
beam.

29. CROSS-SECTION WITH RESPECT TO AXIS:


Again, a structural member
is sometimes analyzed
through its cross-section. It
is essential to note that not
just any cut-section is
called cross-section.
In case of beam, we cut the
beam vertically and found
its cross-section, whereas
we will not get the crosssection of a column if we
cut it vertically, instead we
have to cut it horizontally to
get the cross-section of a
column.

30. 
So we see, even in
getting crosssections, we face the
influence of axis
system. In order to
get a cross-section of
a member, we need
to cut the member
perpendicular to its
major axis.

31. RELEVANCE OF FORCE WITH AXIS SYSTEM:


In analysis of structural
member, we must assess the
type, magnitude and direction
of every kind of forces that act
on the member. The line of
acting force changes along
with the change of major axis.
E.g. - For a normal rectangular
beam of a building, shear force
acts perpendicular to the major
axis of the beam i.e.
perpendicular to ground. But in
case of a column of the same
building the shear force does
not act perpendicular to
ground, instead it acts parallel
to ground.

32. 

Because, in case of
column, the major axis aligns
with its longest dimension (i.e.
the height of column).
Hence, the shear force acts
perpendicular to the major
axis of the column which is
parallel to the ground.
Therefore, the acting line of
shear force changes along
with the major axis of the
structure.
Same rule applies when the
direction of axial force is to be
determined for any structural
member. Only in this case, the
axial force acts parallel to the
major axis of a structural
member.

33. APPLICATION OF AXIS SYSTEM IN MOMENT OF
INERTIA:

It is practically impossible to
analysis a structural member
without estimating its moment
of inertia. Moment of inertia is
an indicator of the stability of
the member. But it is very
important to keep in mind that
along which axis we are
calculating the moment of
inertia. Because if we analyze
this 2D rectangular
member, we find along X-axis
it has maximum moment of
inertia.

34. That means if same amount of moment is
produced along both axes, the member shows
more resistance along X-axis compared to Yaxis. Thus the member will be difficult to bend
along X-axis than Y-axis.
 Therefore, we can estimate along which axis,
moment can be produced to design safe
structures.


35. MOHR’S CIRCLE
Mohr’s circle is one of the important
contents which is also defined by axis
system.
 Mohr’s circle is a geometric representation
of the 2-D transformation of stresses and
is very useful to perform quick and efficient
estimations, checks of more extensive
work, and other such uses.


37. THANK YOU