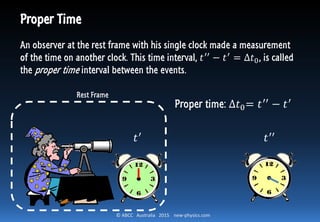
1) Time dilation describes the phenomenon where time passes at different rates for observers in different reference frames that are in motion relative to each other. 2) The proper time between two events is the time interval measured by an observer in the rest frame of the events. For observers in different frames, the time interval is dilated compared to the proper time. 3) Experiments have verified time dilation, such as atomic clocks on airplanes or the lifetime of muons. The twin paradox describes how a twin that travels in a rocket will age less than their identical twin who remains on Earth, even though each twin was stationary in their own reference frame.

1. © ABCC Australia 2015 new-physics.com
TIME DILATION IN RELATIVITY
Cosmic Adventure 5.6

2. © ABCC Australia 2015 new-physics.com
Temporal Transform
Not only frame
transformation changes
the length of an object,
but also the timing on
the object.

3. © ABCC Australia 2015 new-physics.com
Proper Time
An observer at the rest frame with his single clock made a measurement
of the time on another clock. This time interval, 𝑡′′
− 𝑡′
= ∆𝑡0, is called
the proper time interval between the events.
𝑡′′𝑡′
Proper time: ∆𝑡0= 𝑡′′
− 𝑡′
Rest Frame

4. © ABCC Australia 2015 new-physics.com
Proper Time Equation
To find the relationship between the time separations as measured by O
and O’ , the relativistic way is to subtract two of the Lorentz time
transformations:
∆𝑡0= 𝑡′′ − 𝑡′ →
𝑡′′ +
𝑣𝑥′′
𝑐2
1 − 𝑣2 𝑐2
−
𝑡′ +
𝑣𝑥′
𝑐2
1 − 𝑣2 𝑐2
=
𝑡′′
+
𝑣𝑥′′
𝑐2 − 𝑡′
−
𝑣𝑥′
𝑐2
1 − 𝑣2 𝑐2

5. © ABCC Australia 2015 new-physics.com
Resulting Difference
∆𝑡0=
𝑡′′ +
𝑣𝑥′′
𝑐2 − 𝑡′ −
𝑣𝑥′
𝑐2
1 − 𝑣2 𝑐2
These time measurements are made in the moving frame. When they are
made at the same location, the expression will be reduced to:
∆𝑡 =
𝑡′′ − 𝑡′
1 − 𝑣2 𝑐2
=
∆𝑡0
1 − 𝑣2 𝑐2
= 𝛾∆𝑡0
Where 𝛾 =
1
1− 𝑣2 𝑐2

6. © ABCC Australia 2015 new-physics.com
Time Dilation
Since: 1 − 𝑣2 𝑐2 < 1,
∆𝑡 > ∆𝑡0
Being the time interval
between the two events
measured by O’ is
considered to be dilated
(enlarged), thereby giving
rise to the phenomenon of
“time dilation”.

7. © ABCC Australia 2015 new-physics.com
Equation of Time Dilation
∆𝑡 =
∆𝑡0
1 − 𝑣2 𝑐2
Observed time Proper time
Lorentz Factor

8. © ABCC Australia 2015 new-physics.com
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
10.0
8.0
6.0
4.0
2.0
1.0
Timedilation
∆𝑡 =
∆𝑡0
1 −
𝑣2
𝑐2
Velocity as a fraction of the speed of light
𝑣/𝑐

9. © ABCC Australia 2015 new-physics.com
Time Changes due to
Frame Transfer
For example, one can place
cameras at the location of
clock B and at the location of
the clock C, and a picture is
taken by each camera when the
clock C passes clock B.
Each picture will show that the
clock C has advanced through
∆𝑡0 while clock B has
advanced through ∆𝑡.
∆𝑡 and ∆𝑡0 are related by the
time dilation equation.
Clock A Clock BClock B
Clock C
Clock C
𝑣
𝑣
Clock C advances
through ∆𝑡 𝑜
Clock A & B advances through ∆𝑡

10. © ABCC Australia 2015 new-physics.com
Slower Clocks
For the observer at
rest on the ground,
the object’s clock is
running at a lower
rate. But for the clock
carrier, there is no
difference at all. His
clock is running at the
normal rate as when
he is at rest.
No! It is
not!
Your clock is
slowing down!

11. © ABCC Australia 2015 new-physics.com
Time Lapse by Slower Clock
Once the moving clock re-
unites with the ground clock, it
will again run at the same rate
as the ground clock. It is only
when the clock is in motion
with respect to the other clock
that the phenomenon of time
dilation takes place.
Naturally, the slower clock will
remain behind by the amount
of time it spent.

12. © ABCC Australia 2015 new-physics.com
Time Dilation is Retained
by Slower Clock
Relativists believe that if you
take two very accurate and
well synchronized atomic
clocks and put one on a
high-speed trip on an
airplane. When the plane
returned, the clock that took
the plane ride was slower.

13. © ABCC Australia 2015 new-physics.com
The Twin Paradox
The wonderful thing is that
the returned clock keeps the
time it gained in the trip.
Anyone who travels with the
clock will consequently live
longer. This leads to the
phenomenon of “Twin
Paradox”. It is a paradox
because nobody has verified
it by trying to live longer
this way.

14. © ABCC Australia 2015 new-physics.com
Dr. Einstein will return to earth nearly as young, while his twin on earth
will have aged terribly.

15. © ABCC Australia 2015 new-physics.com
Example of Calculation
The earth bound Einstein calculate the time dilation with the equation:
∆𝑡 =
∆𝑡0
1 − 𝑣2 𝑐2
where:
∆𝑡 = time observed in the other reference frame
∆𝑡0 = time in observers own frame of reference (rest time)
𝑣 = the speed of the moving rocket
𝑐 = the speed of light in a vacuum

16. © ABCC Australia 2015 new-physics.com
Calculating the Dilation
So in the situation we will let:
𝑣 = .95𝑐
𝑡0 = 10 𝑦𝑒𝑎𝑟𝑠
and we will solve for t which
is the time that the earth
bound Einstein brother
measures.
𝑡 =
10
1 −
0.95𝑐 2
𝑐2
=
10
1 − 0.9025
=
10
0.0975
=
10
0.3122
= 32
𝑇𝑖𝑚𝑒 = 32 𝑦𝑒𝑎𝑟𝑠

17. © ABCC Australia 2015 new-physics.com
Muon Life Time
The extended lifetime of the
muon provides another
proof of time dilation. But so
far the results are not
absolutely precise and the
relativistic explanation is not
too clear. There are other
ways of achieving the results
and in a more logical way.
We will be glad to talk about
it in a different session.

18. © ABCC Australia 2015 new-physics.com
Both Answers Real and Correct
Objectively speaking, the
observer is seeing two different
times.
So which time is correct?
According to the relativists, they
both are.
The reason is that time is not
absolute but is relative, it
depends on the relative
relationship of the reference
frames.
So why then is the
phenomenon called a
paradox?

19. © ABCC Australia 2015 new-physics.com
VISONIC TIME DILATION – CLOCKS AT REST
To be continued on：
Cosmic Adventure 5.7