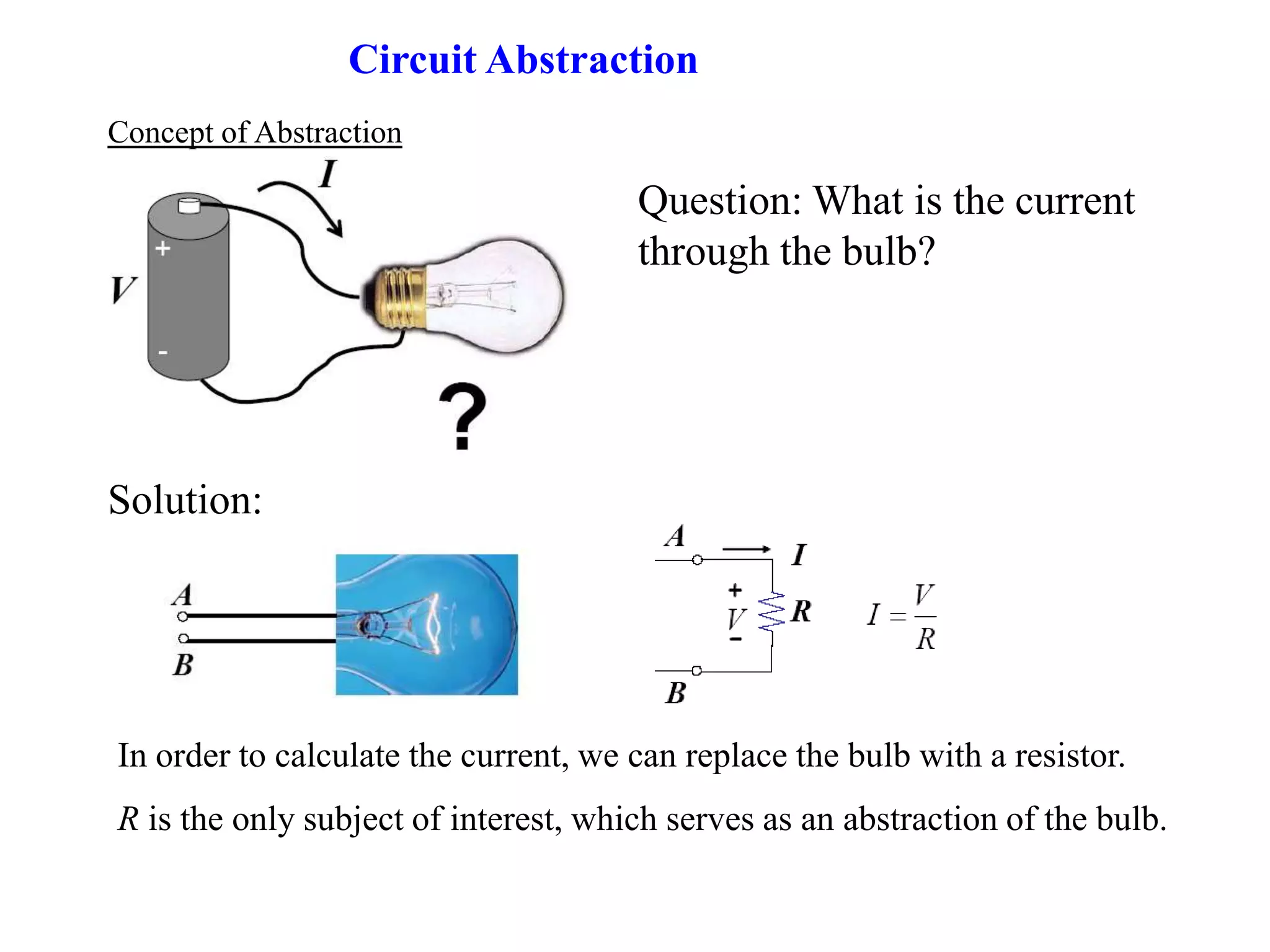
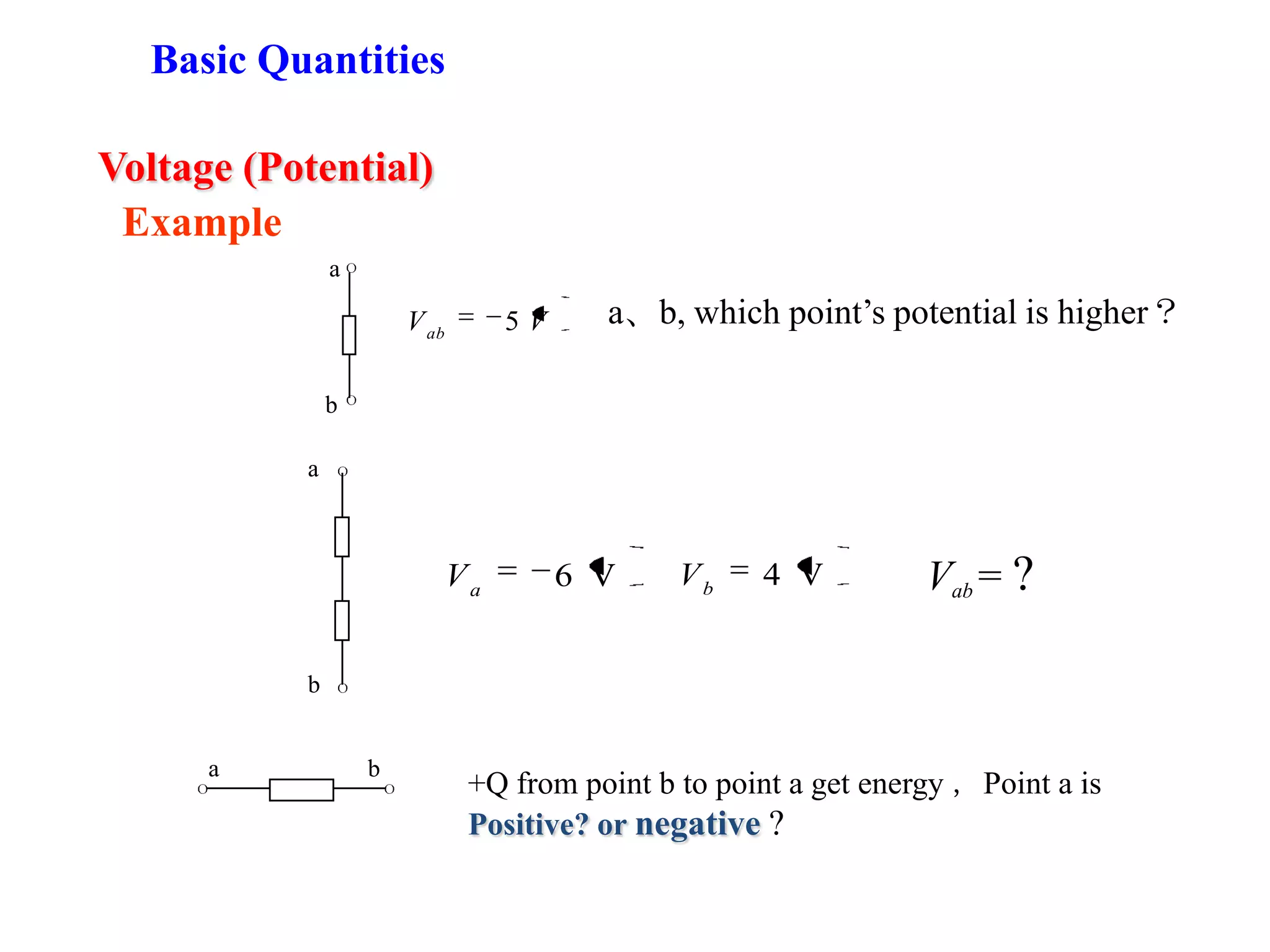
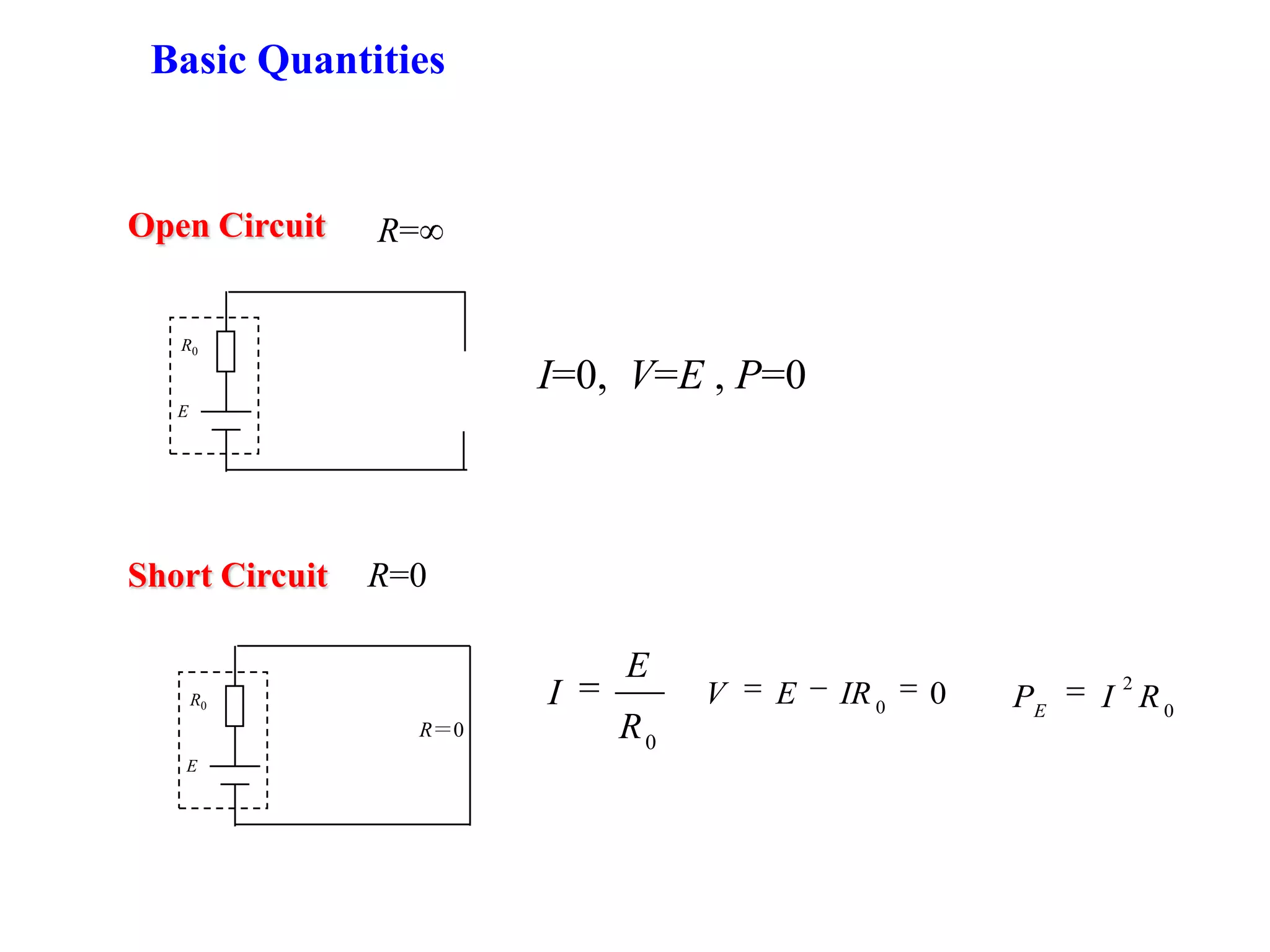
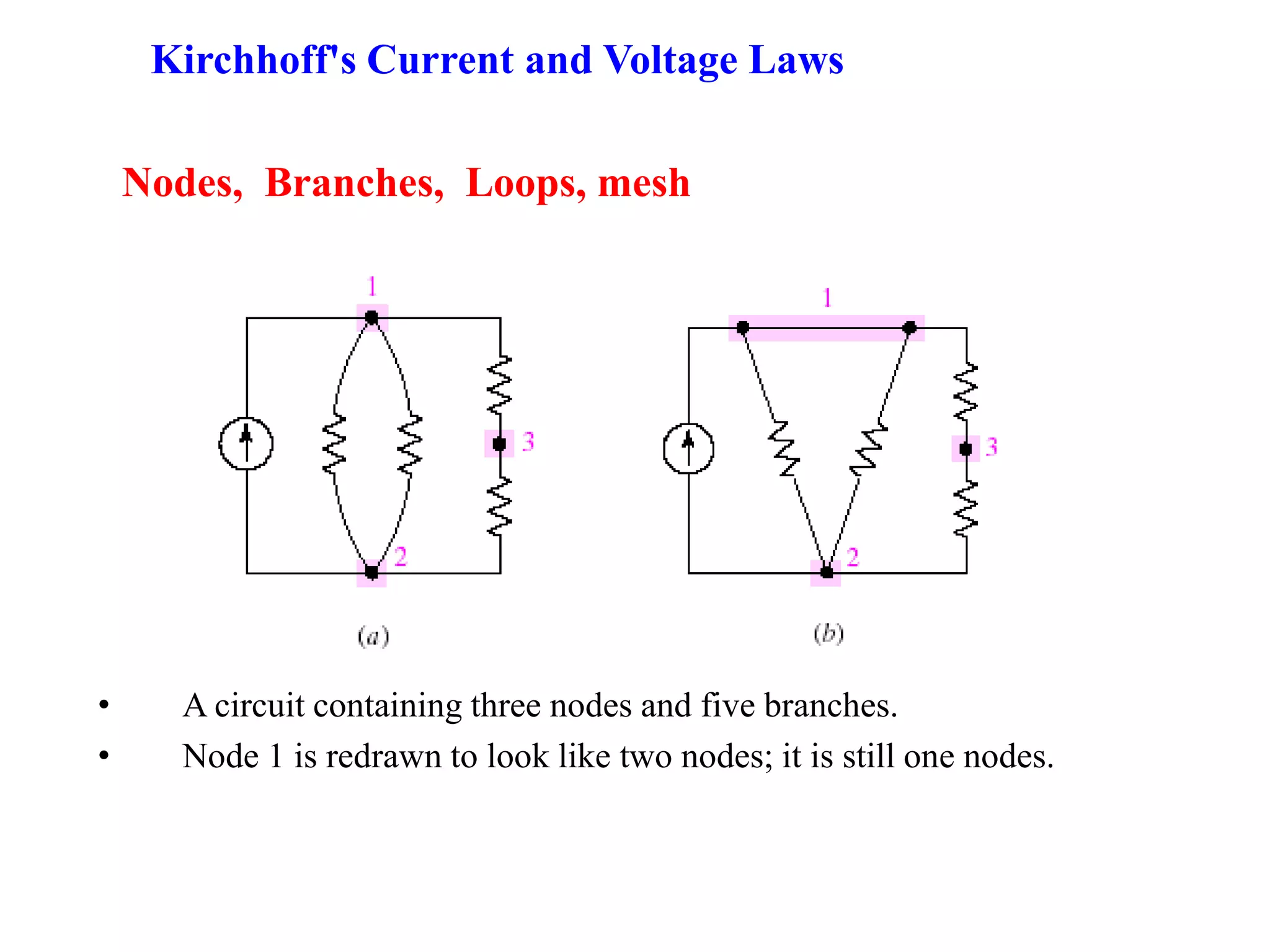
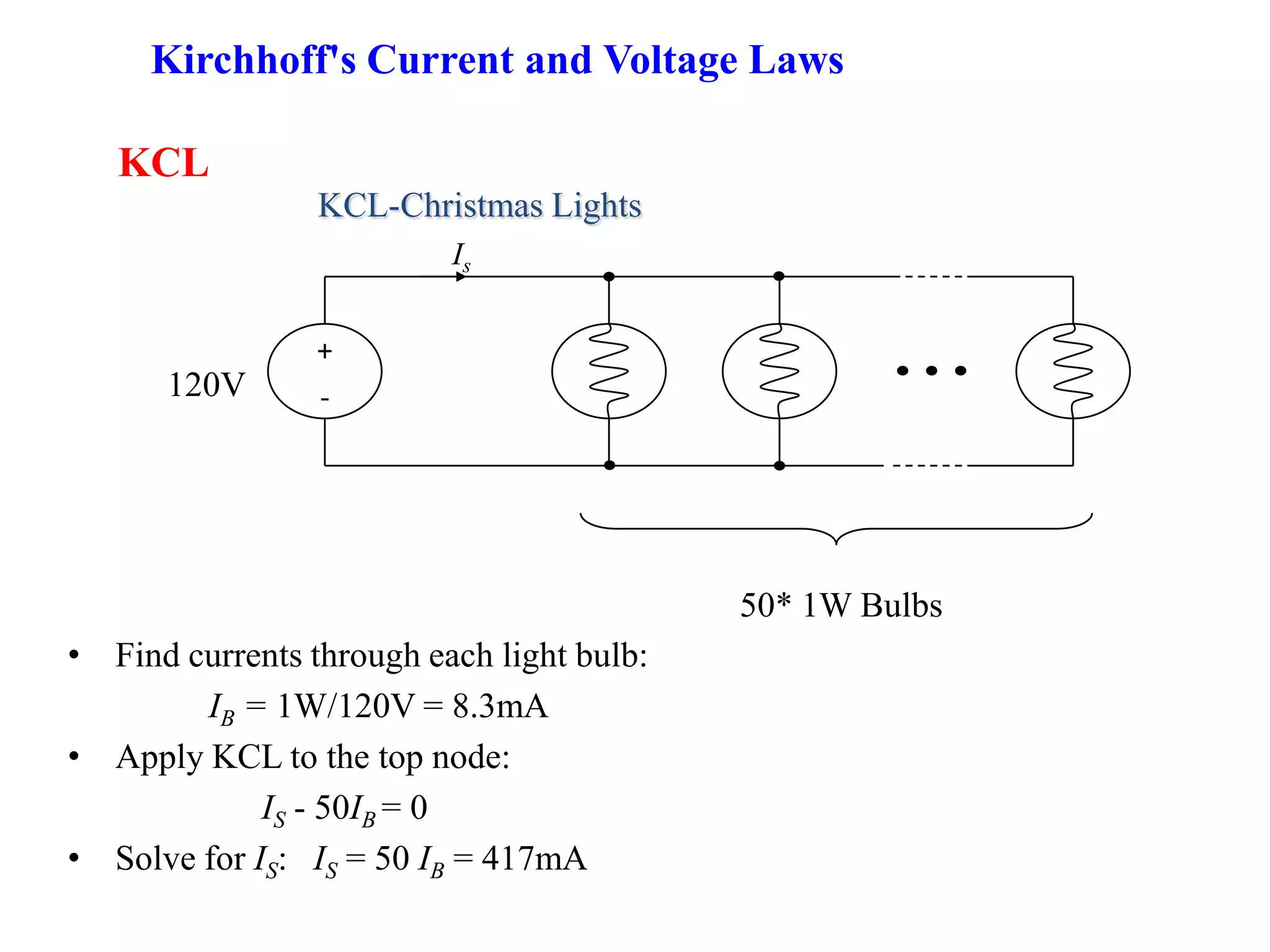
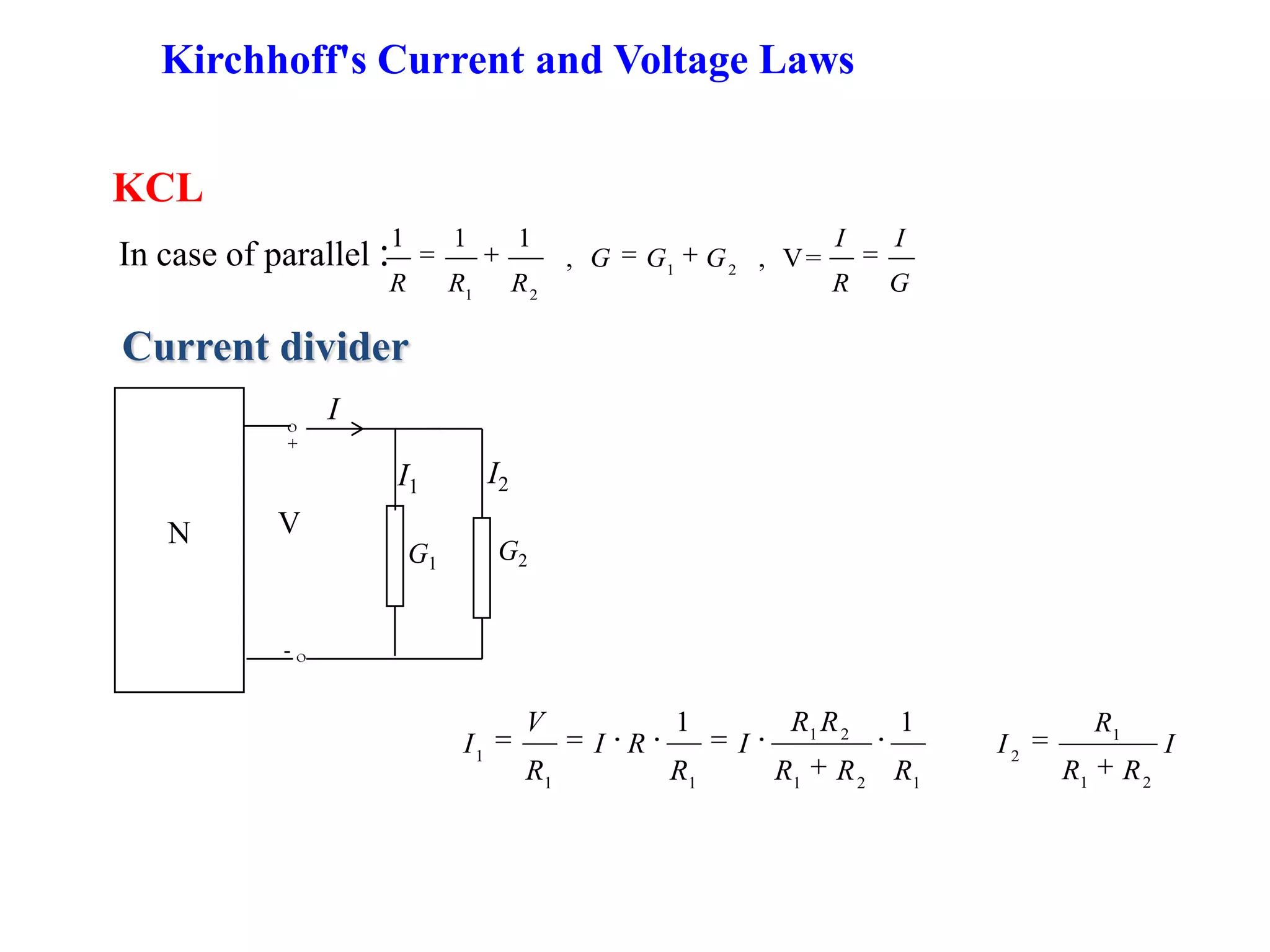
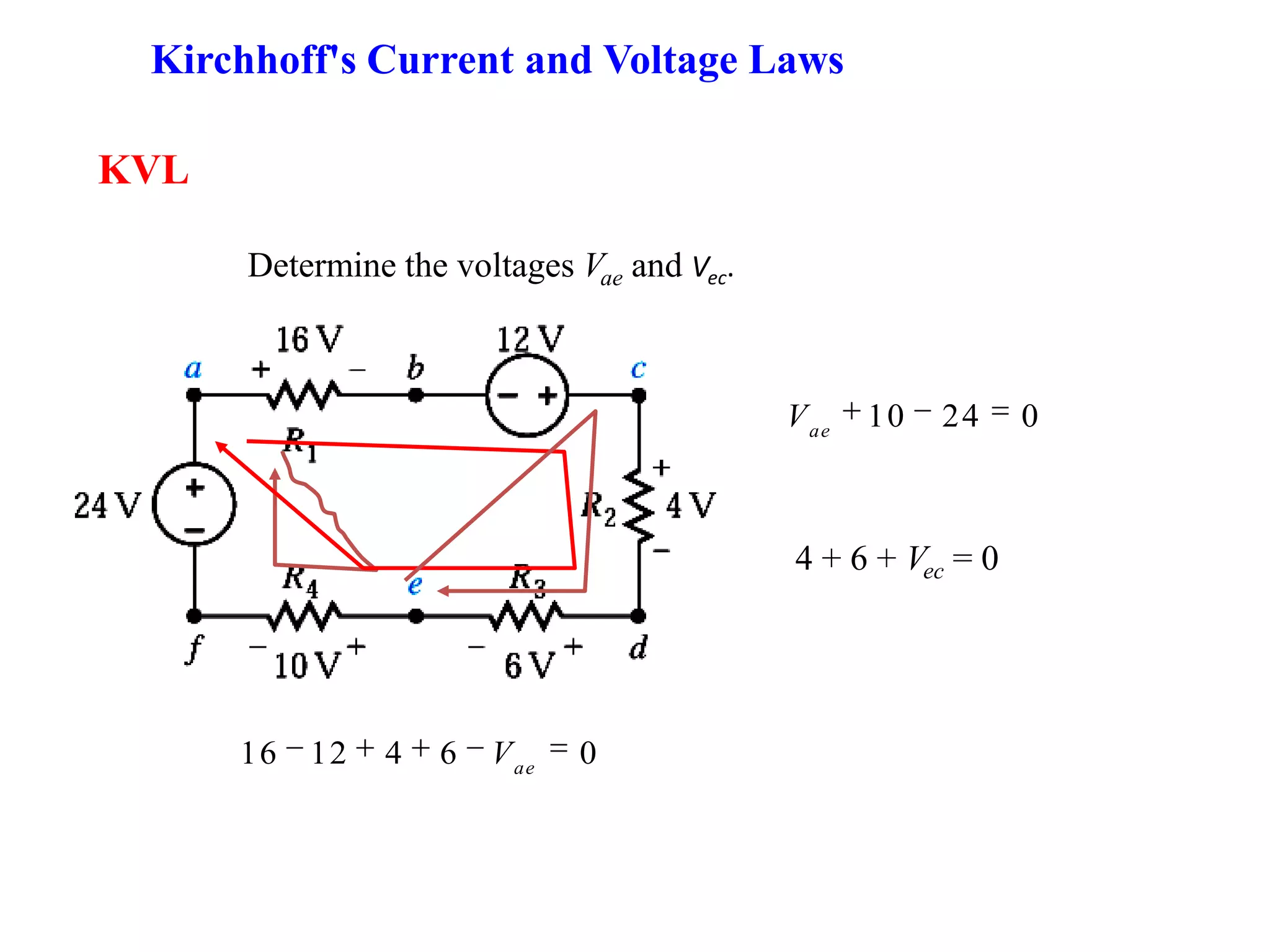
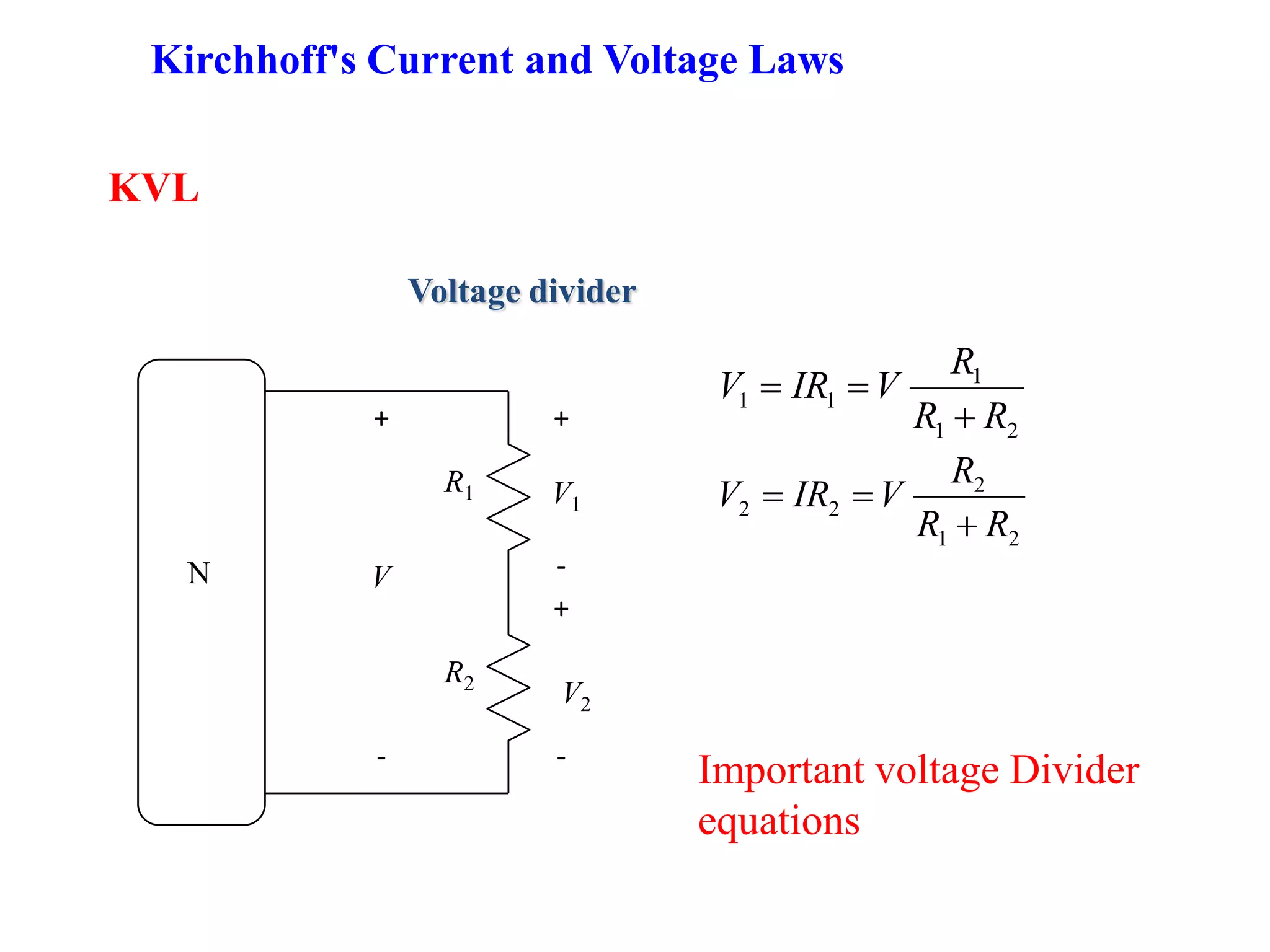
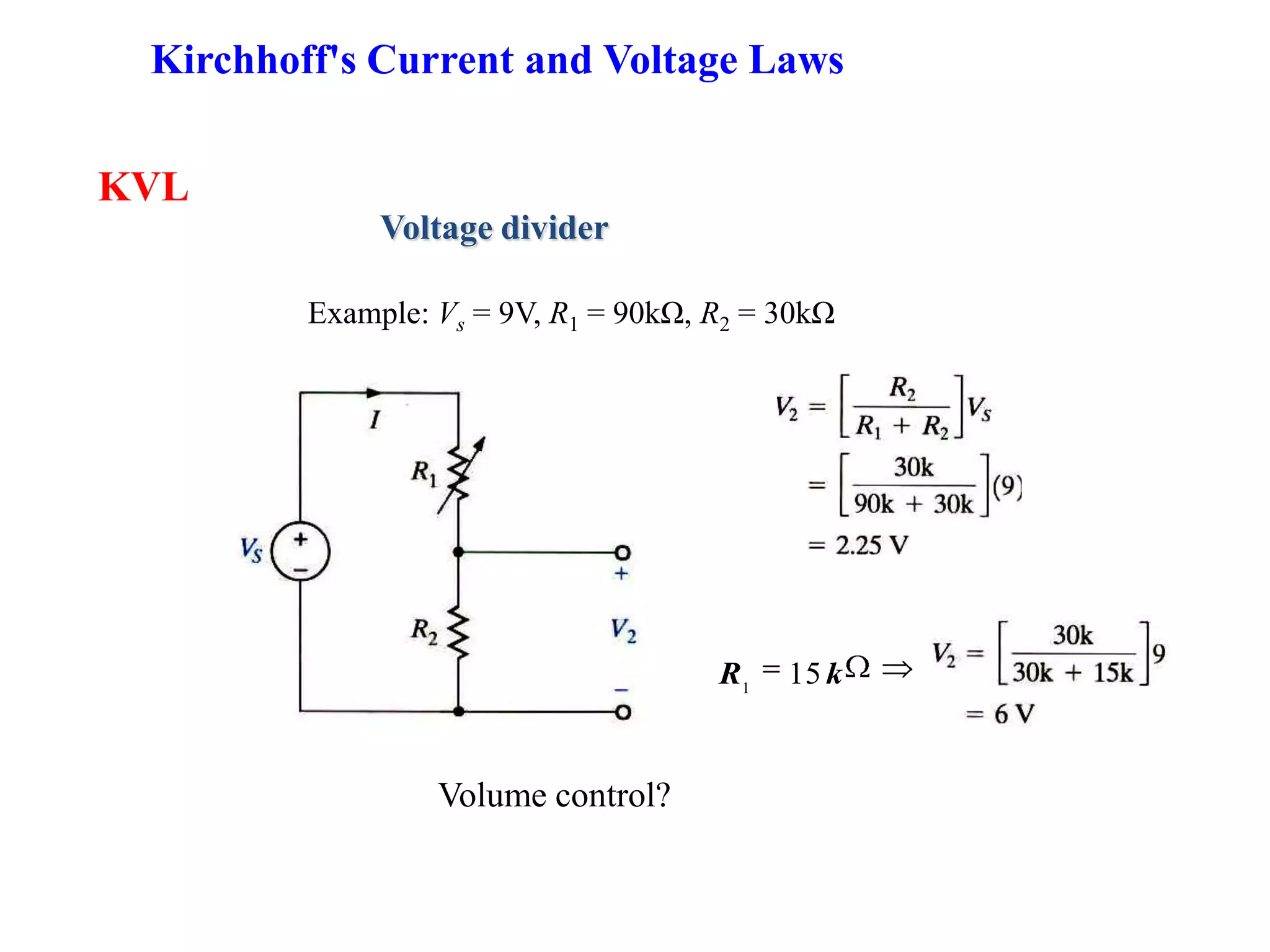
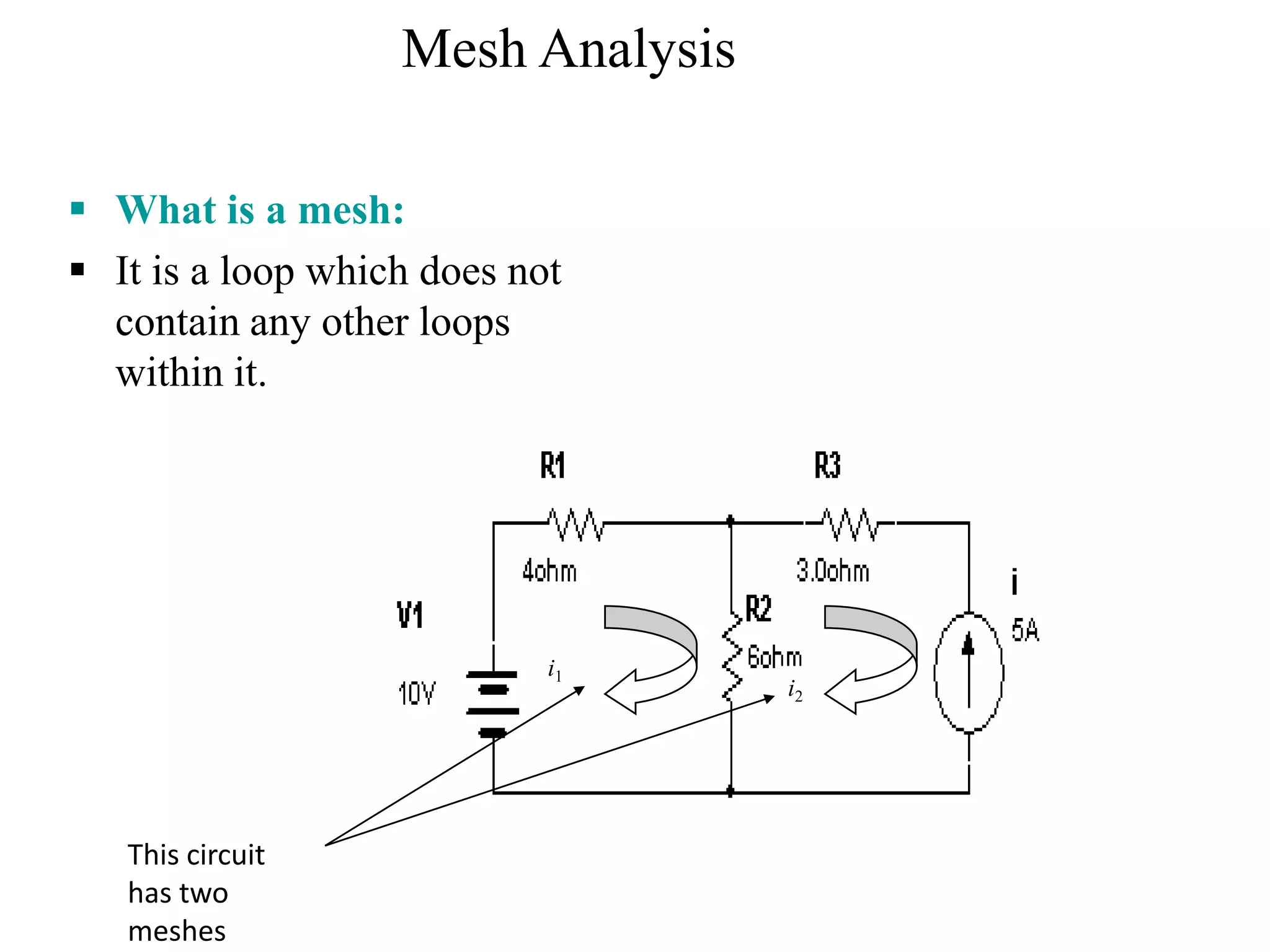
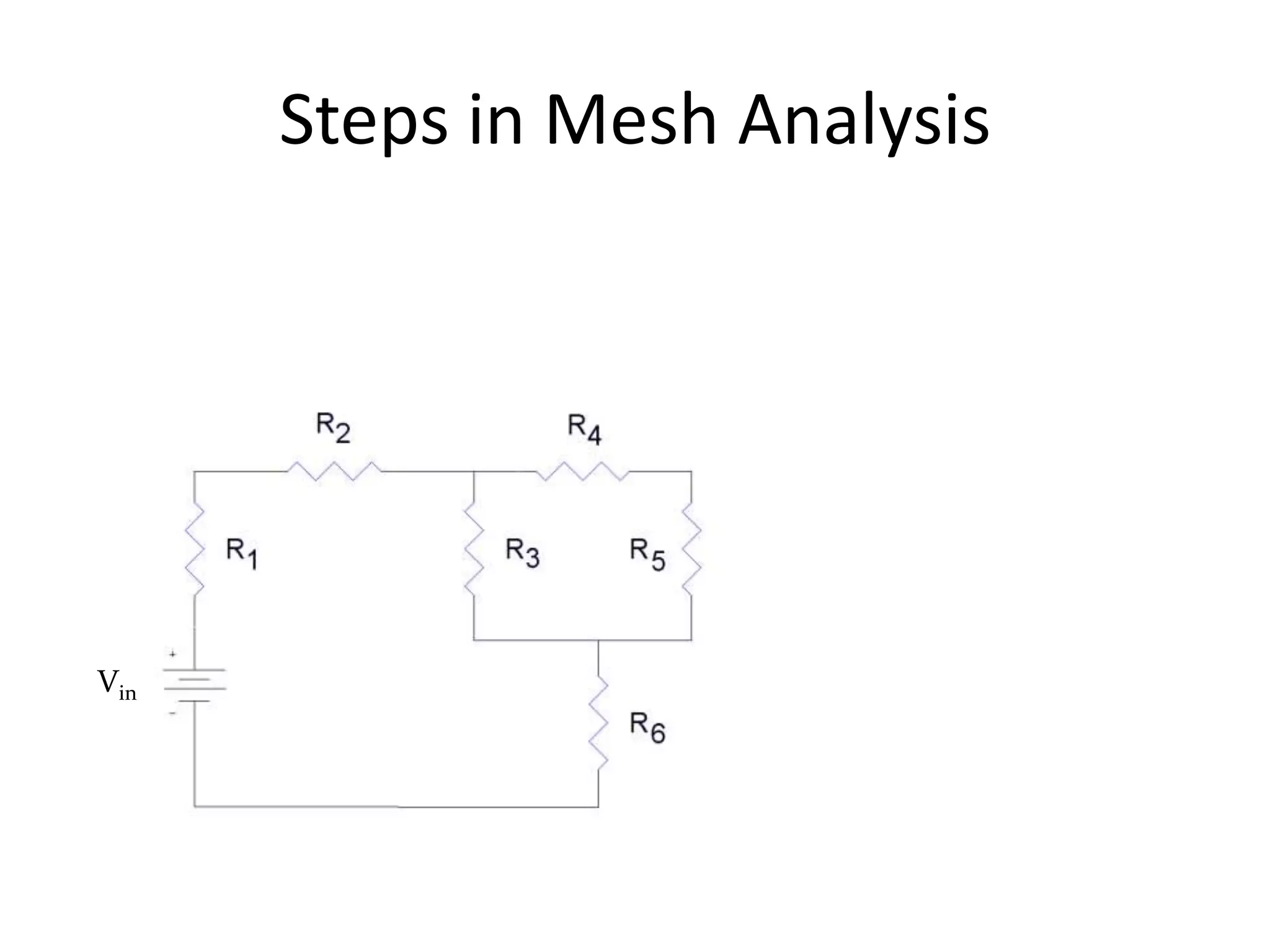
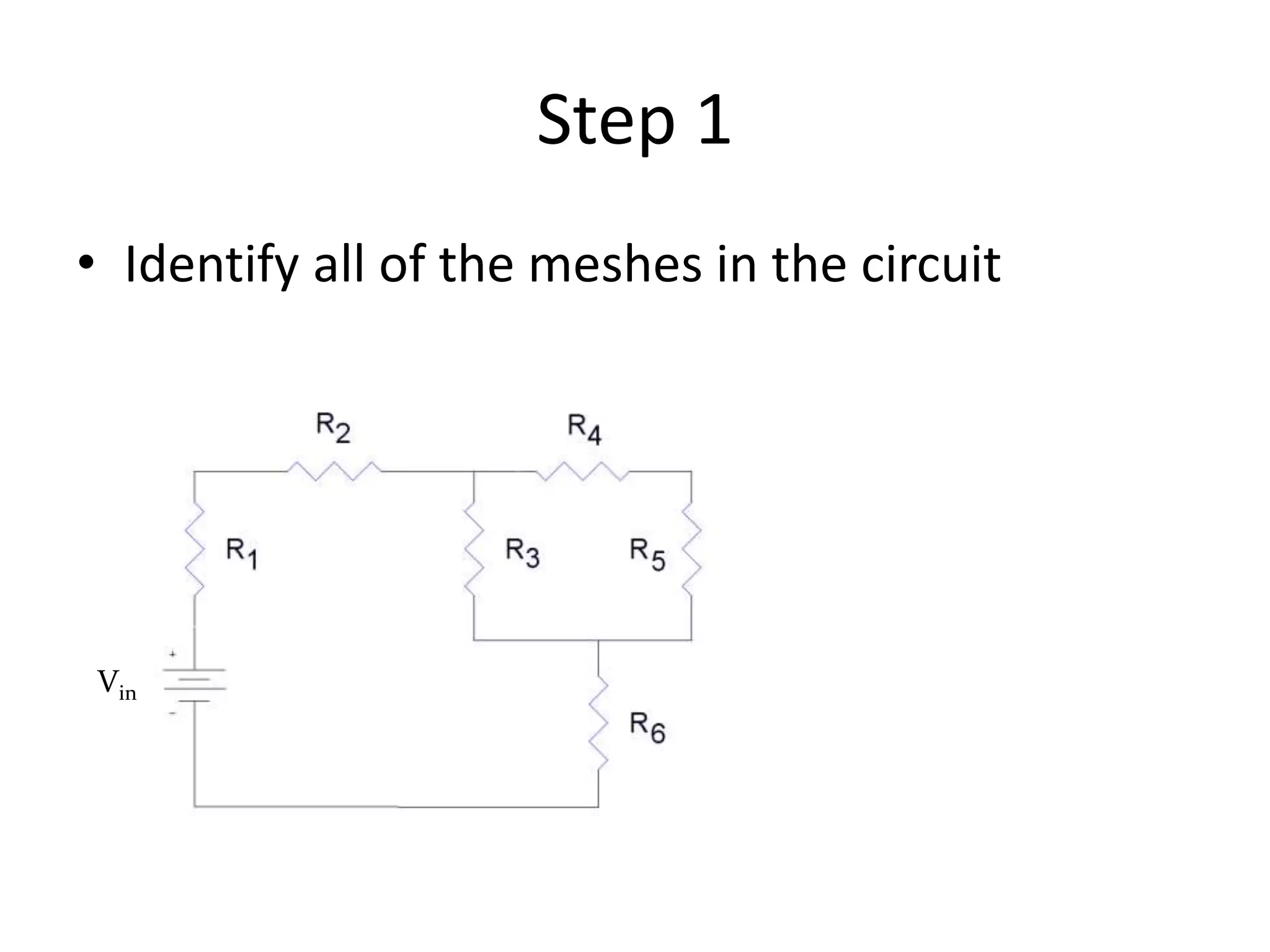
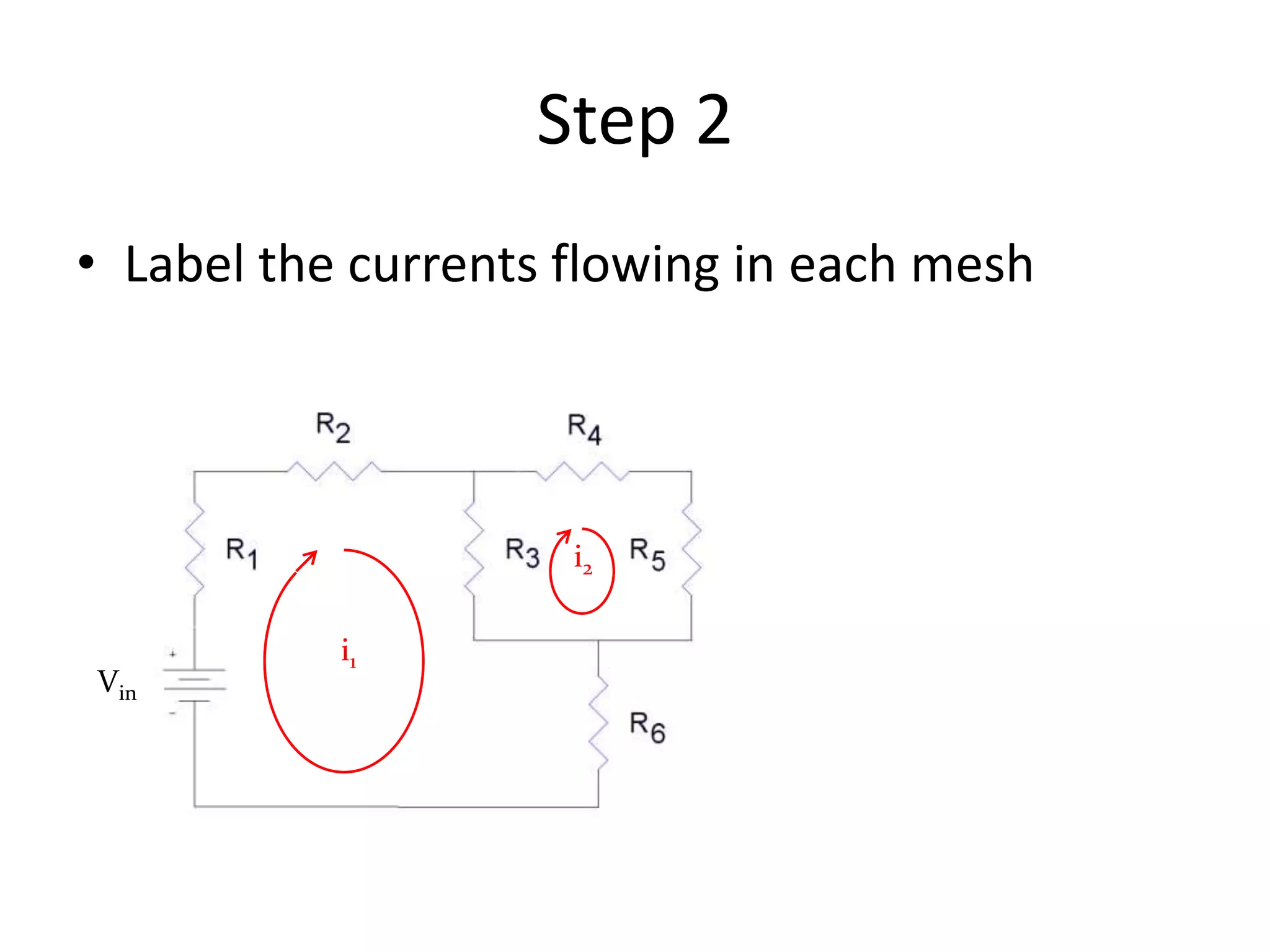
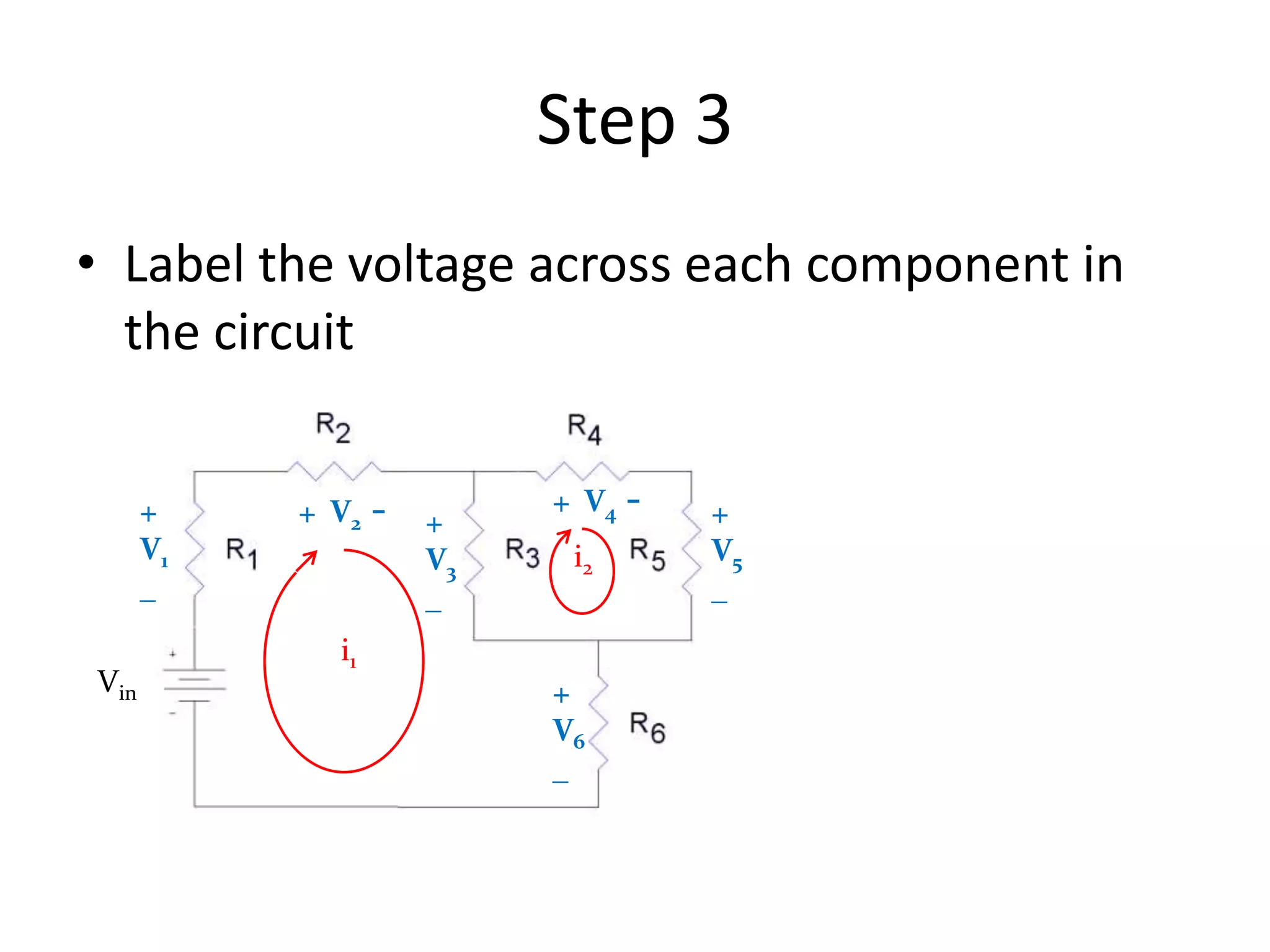
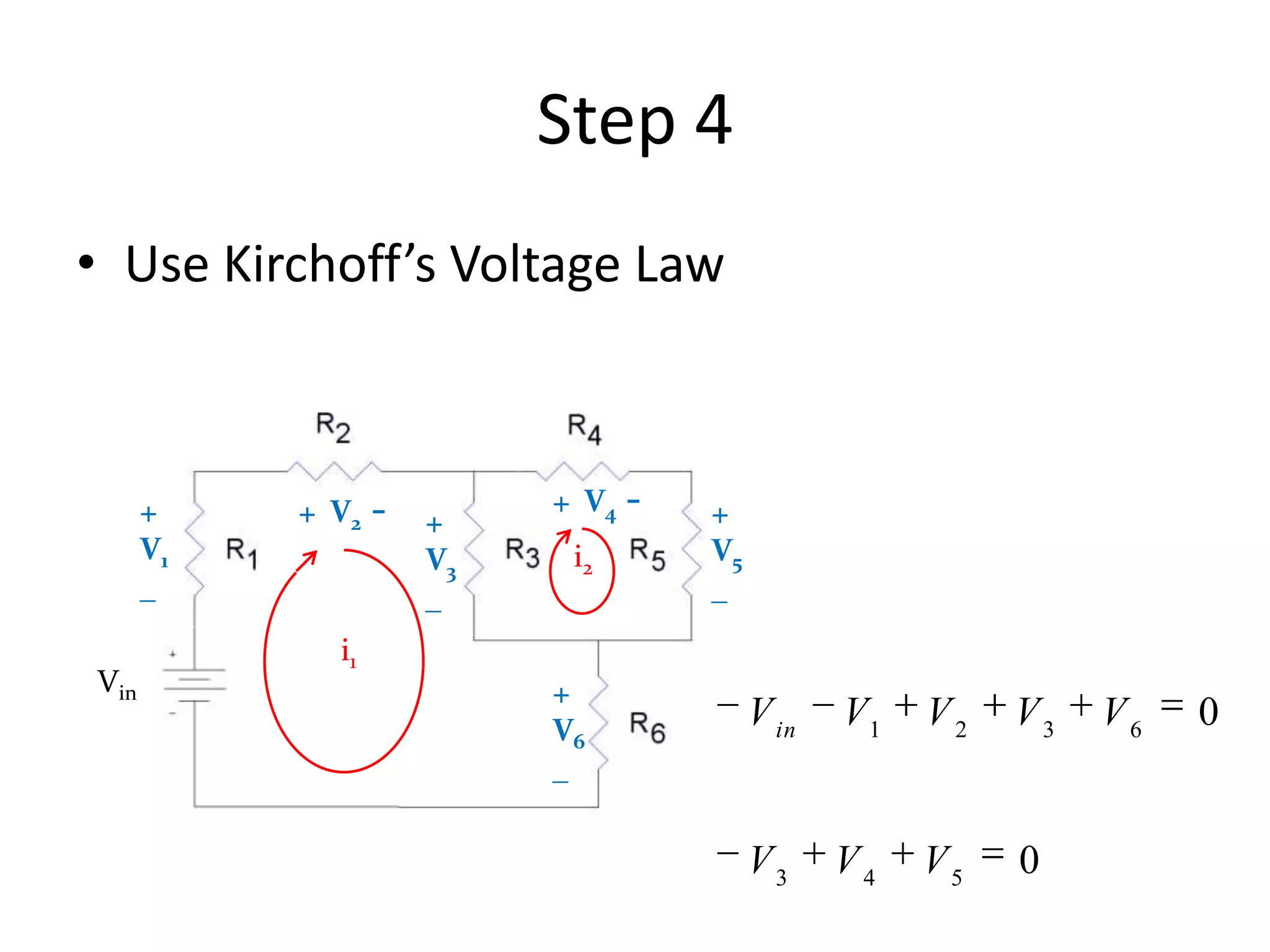
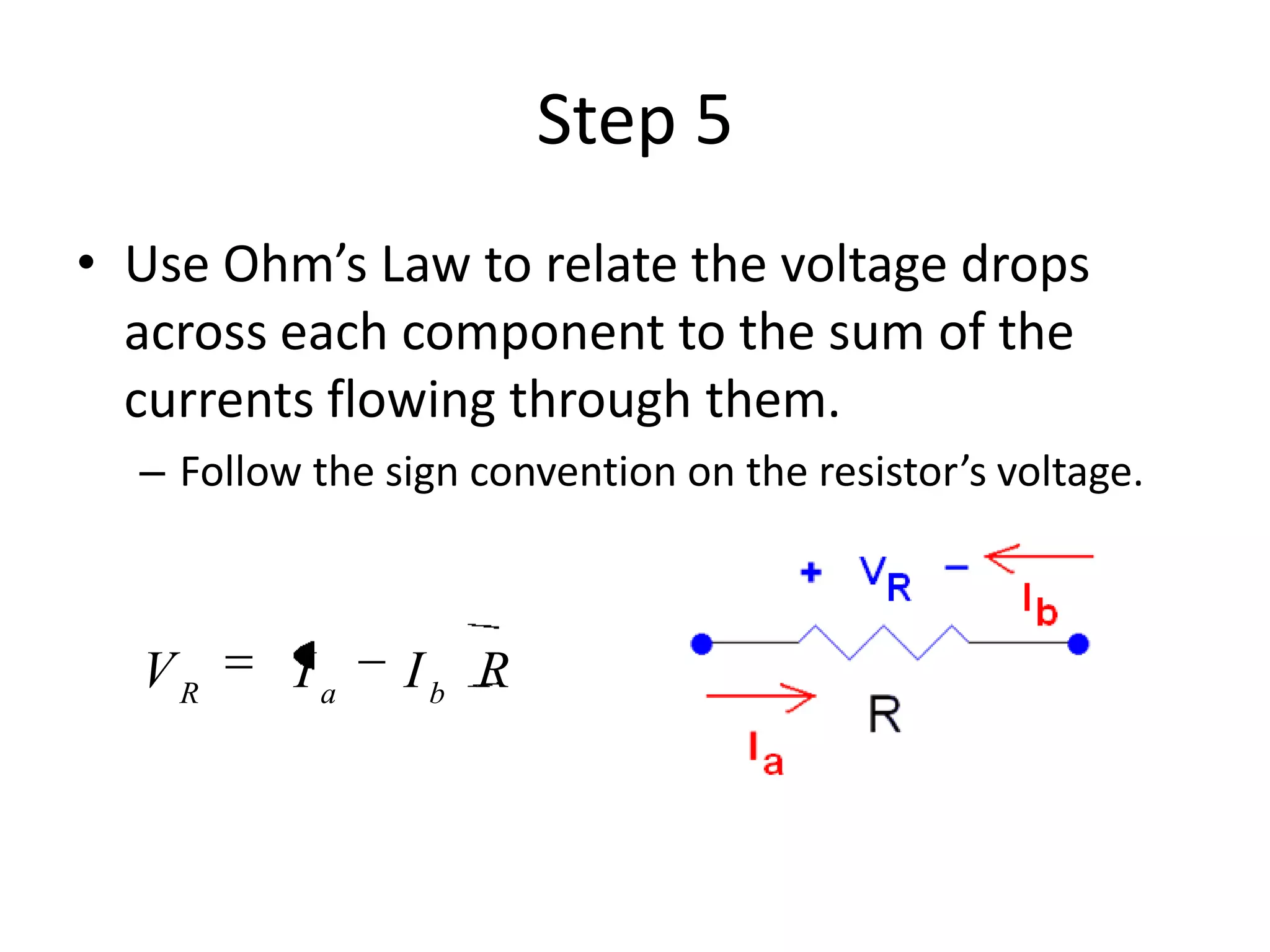
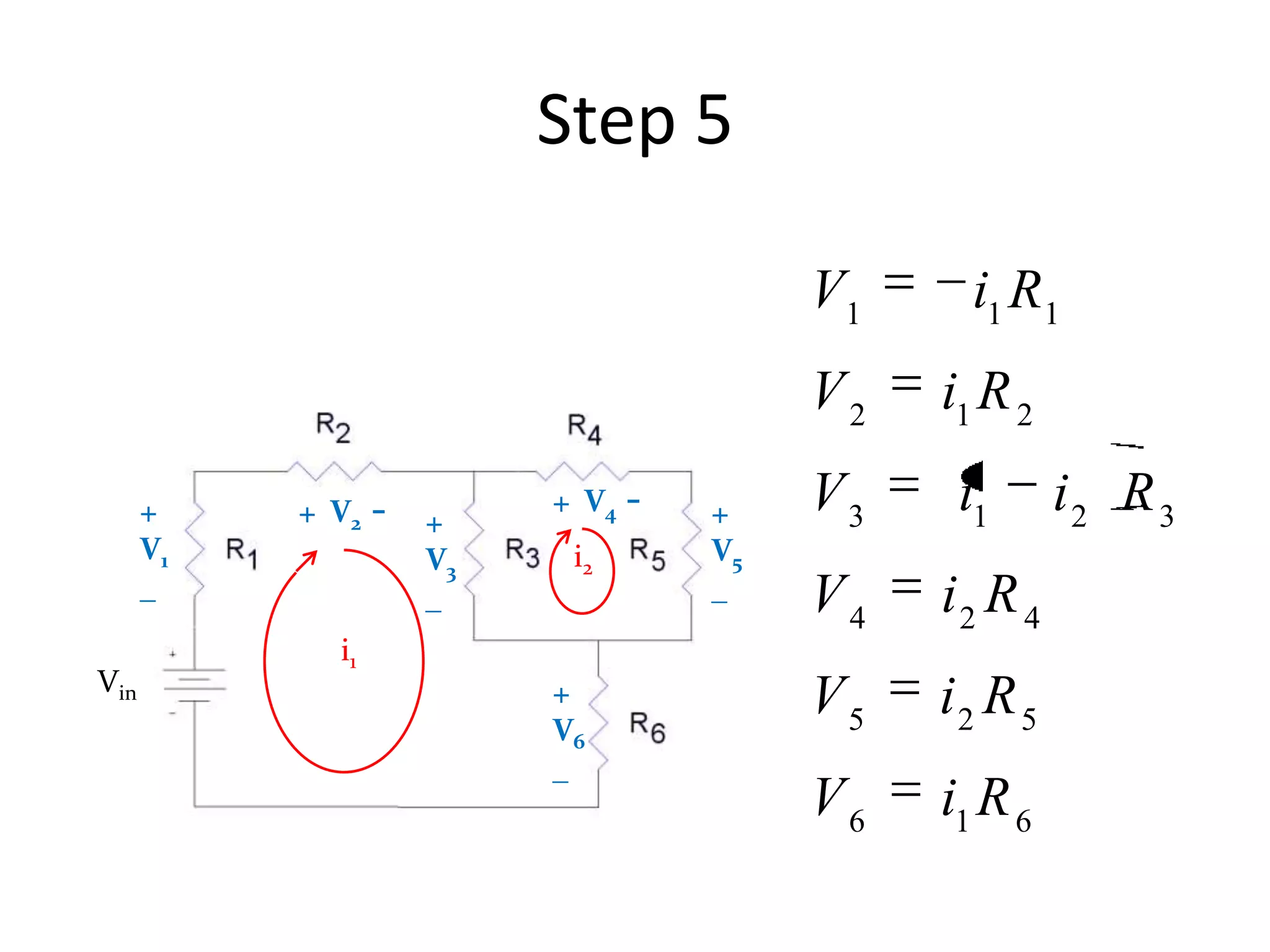
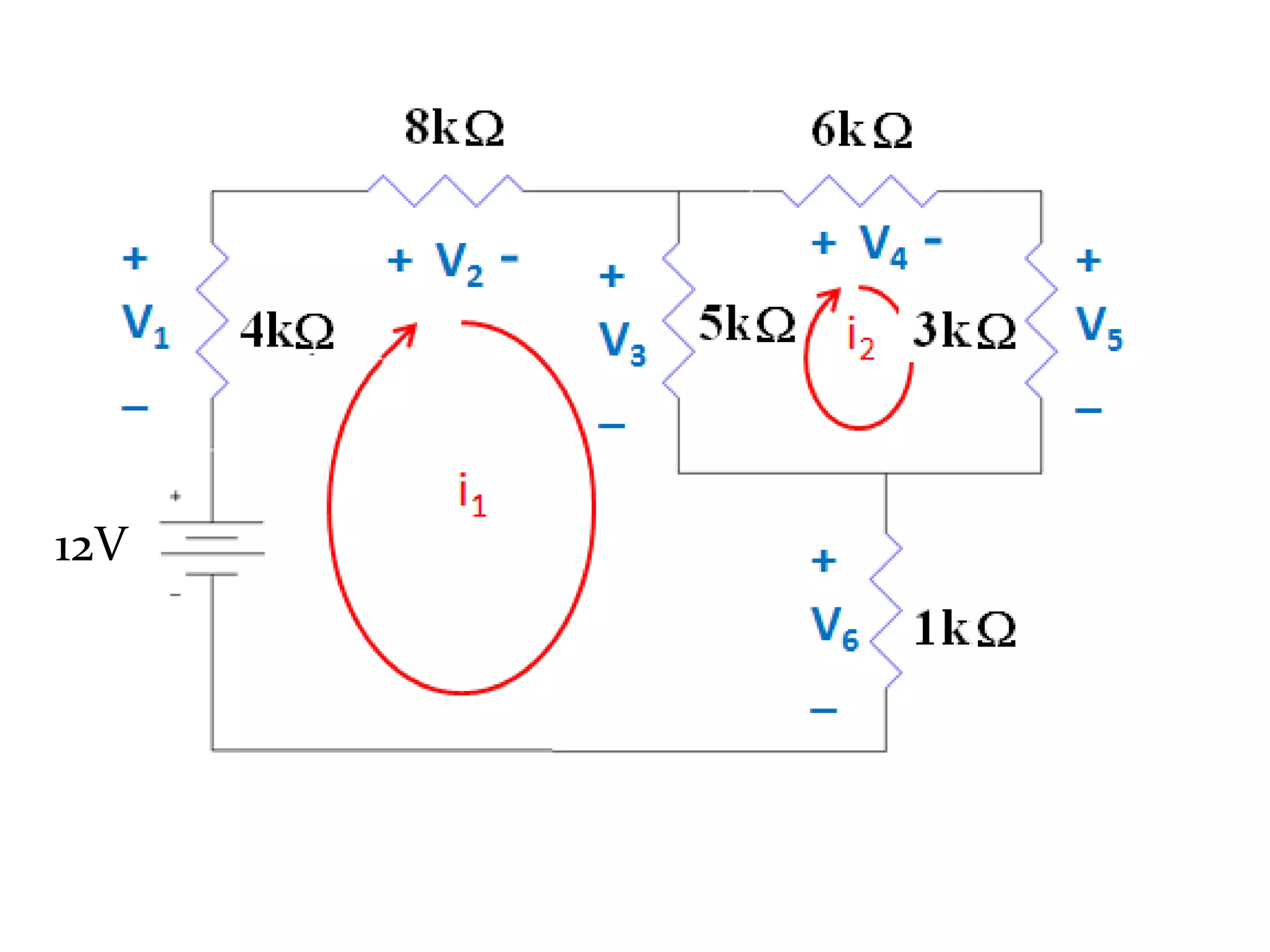
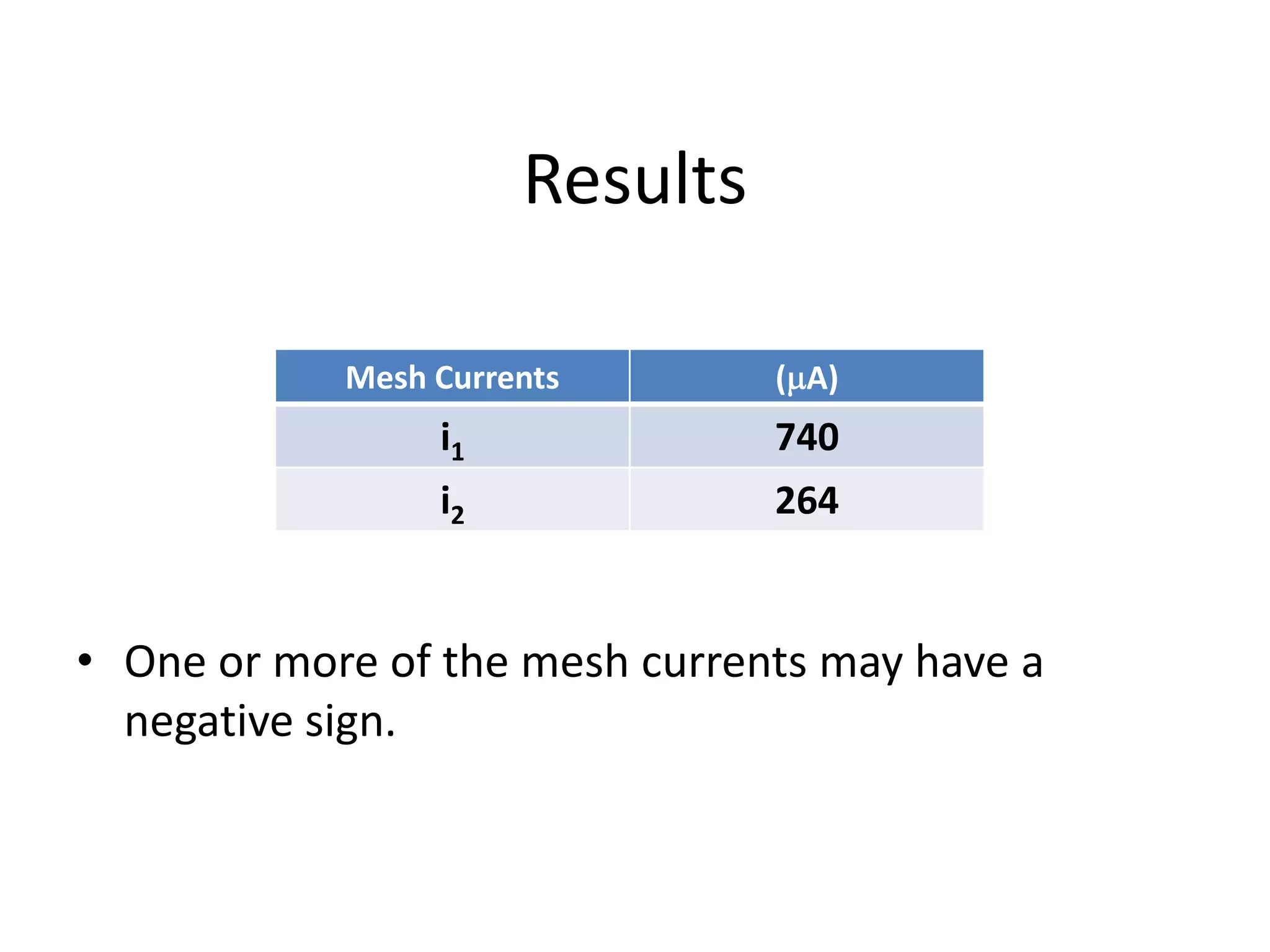
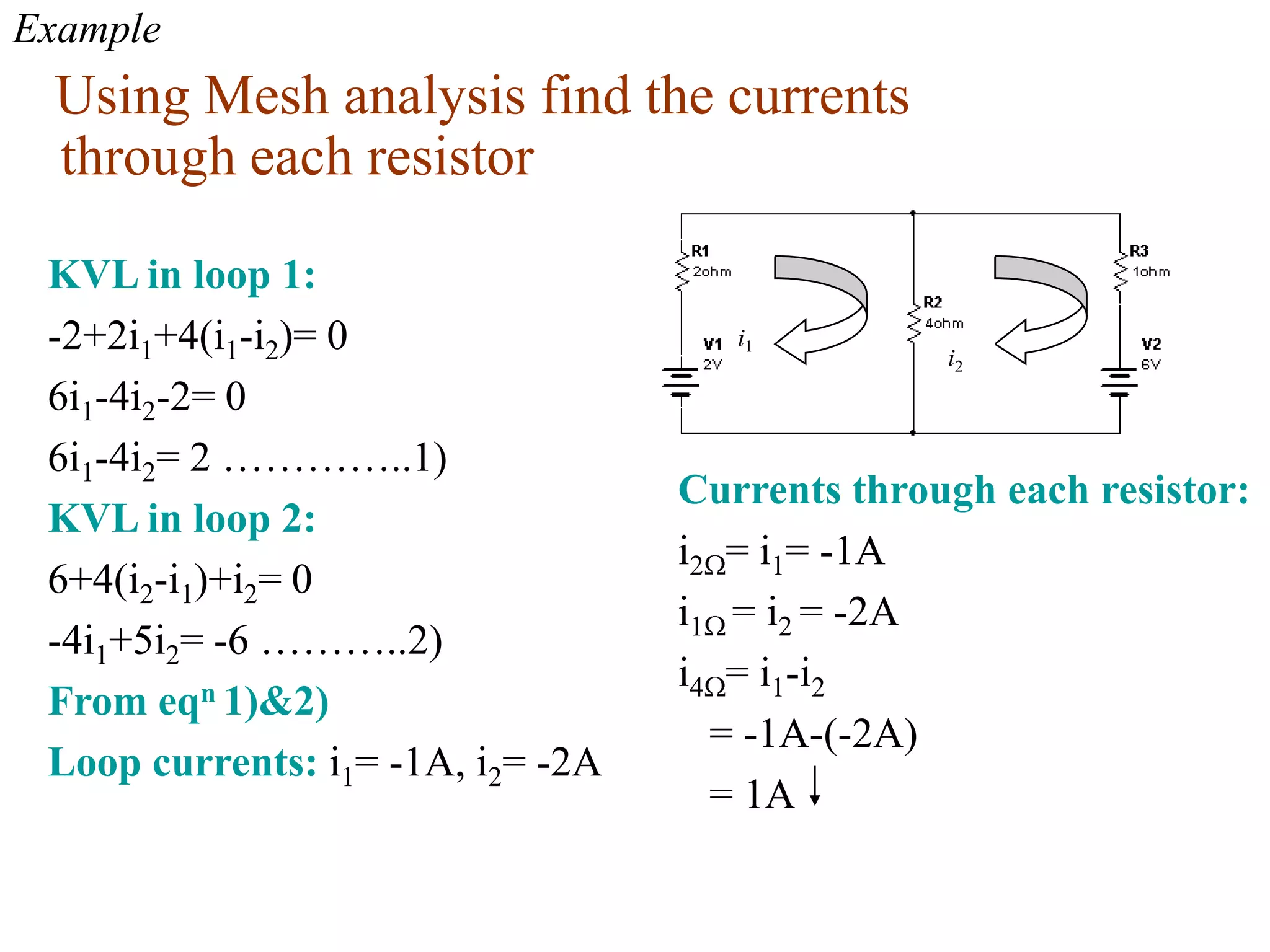
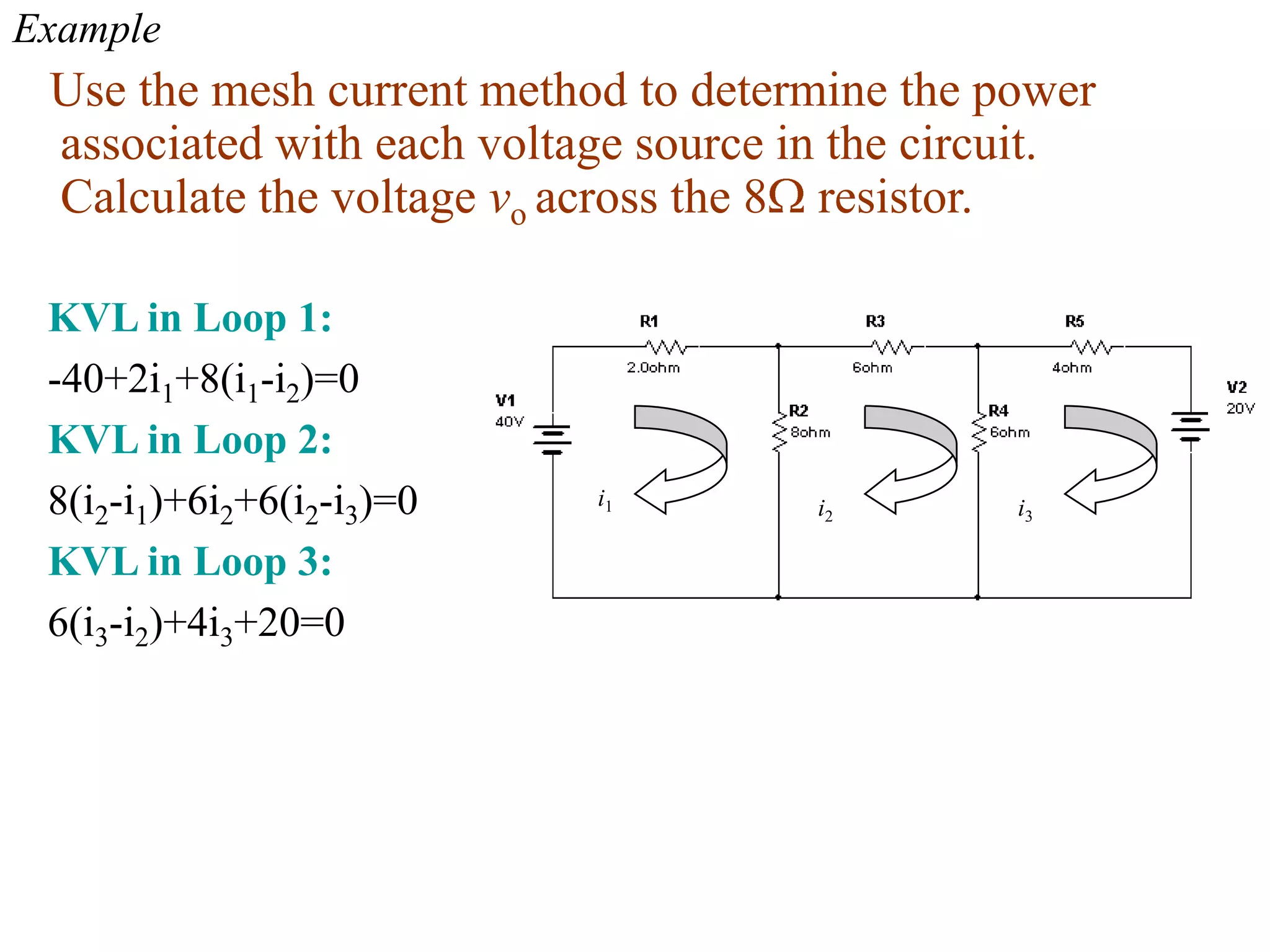
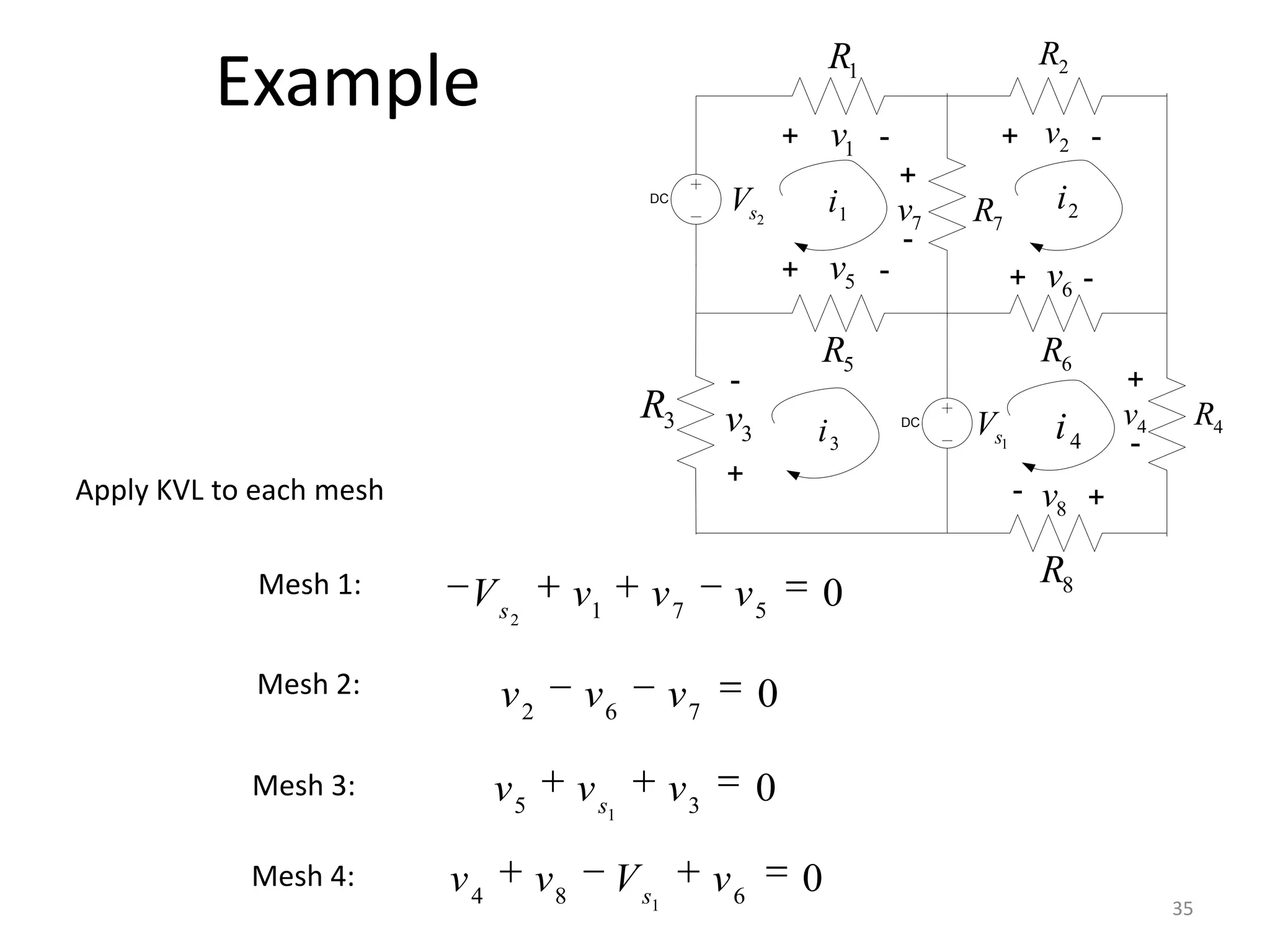
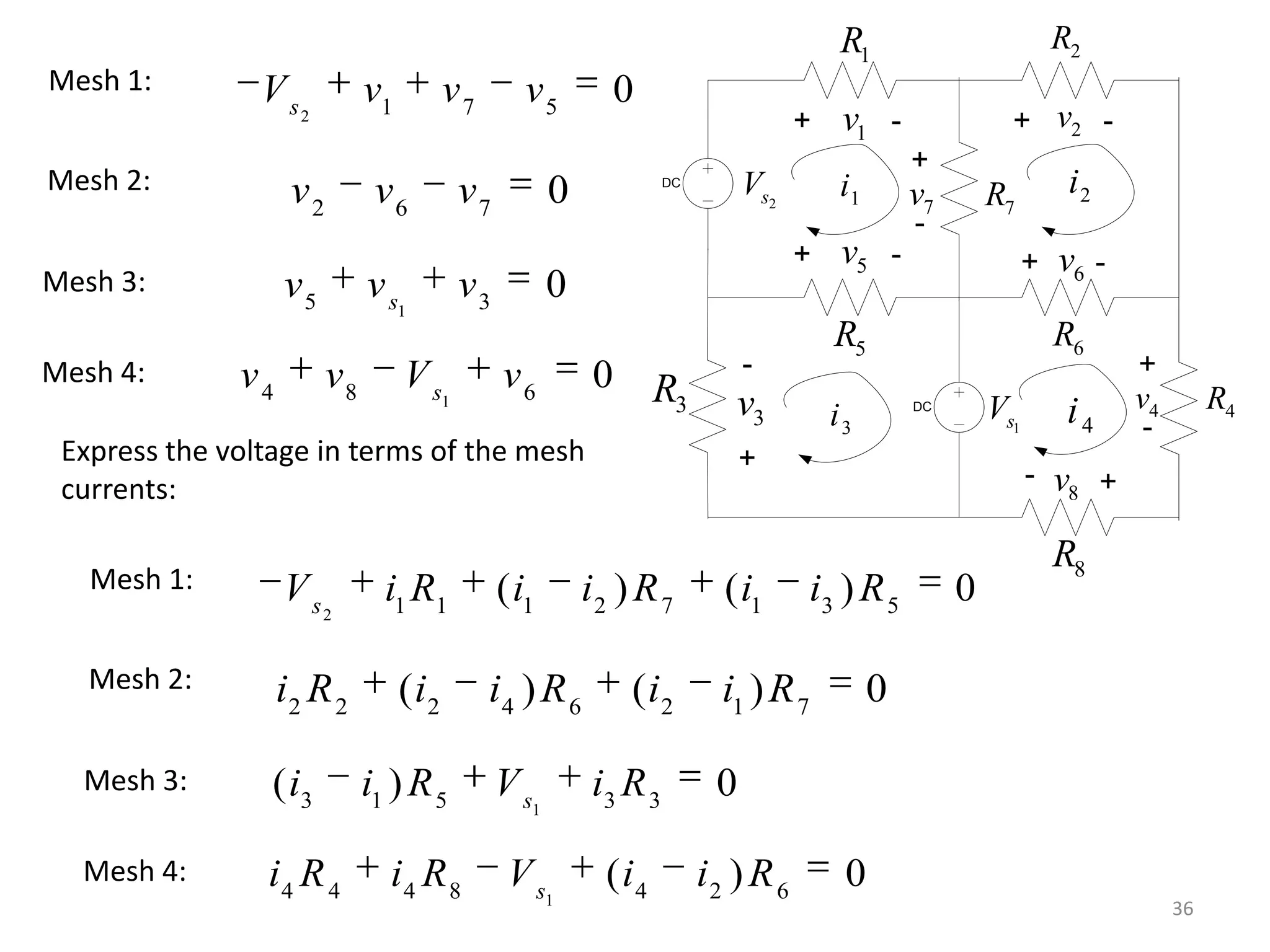
1) The document discusses basic circuit analysis techniques including circuit abstraction, voltage, current, resistance, nodes, branches, loops, and Kirchhoff's laws. 2) Key circuit concepts covered are open and short circuits, voltage and current division, and mesh analysis. 3) Mesh analysis involves identifying all loops in a circuit, labeling loop currents, applying Kirchhoff's laws, and solving equations to determine the currents through each component.

1. Electric Circuit Analysis
Basic analysis techniques
Ahsan Khawaja
Ahsan_khawaja@comsats.edu.pk
Lecturer
Room 102
Department of Electrical Engineering

2. Circuit Abstraction
Question: What is the current
through the bulb?
Concept of Abstraction
Solution:
In order to calculate the current, we can replace the bulb with a resistor.
R is the only subject of interest, which serves as an abstraction of the bulb.

3. Voltage (Potential)
a
b
VVab
5 a、b, which point’s potential is higher？
b
a
V6a
V V4b
V Vab = ?
a b
+Q from point b to point a get energy ，Point a is
Positive? or negative ?
Basic Quantities
Example

4. Voltage (Potential)
ab
c´
c d
d´
2211
21
221121222
2
21112
1111
111
1b1bb
0
)(
)(
,
0
rRrR
EE
I
rRrRIEEIrEVIrVV
EVV
RrRIEIRVV
rRIEIrVV
IREVEV
IRVIRVVVV
V
dda
dd
cd
cc
bc
aab
a
Basic Quantities
Example
I

5. Open Circuit R=
I=0, V=E , P=0
E
R0
Short Circuit R=0
E
R0
R＝0
0
R
E
I 00
IREV 0
2
RIPE
Basic Quantities

6. Nodes, Branches, Loops, mesh
• A circuit containing three nodes and five branches.
• Node 1 is redrawn to look like two nodes; it is still one nodes.
Kirchhoff's Current and Voltage Laws

7. • sum of all currents entering a node is zero
• sum of currents entering node is equal to sum of currents leaving node
KCL
KCL Mathematically
i1(t)
i2(t)
i4(t)
i5(t)
i3(t)
n
j
j
ti
1
0)(
n
j
jI
1
0
Kirchhoff's Current and Voltage Laws

8. • sum of all currents entering a node is zero
• sum of currents entering node is equal to sum of currents
leaving node
KCL
P1.9
DCBA
iiii
Kirchhoff's Current and Voltage Laws
In
Out
0A B C O
I
I
i i i i

9. KCL
+
-120V
50* 1W Bulbs
Is
• Find currents through each light bulb:
IB = 1W/120V = 8.3mA
• Apply KCL to the top node:
IS - 50IB = 0
• Solve for IS: IS = 50 IB = 417mA
KCL-Christmas Lights
Kirchhoff's Current and Voltage Laws

10. KCL
Current divider
N V
G1
G2
I
+
-
I1 I2
121
21
11
1
11
RRR
RR
I
R
RI
R
V
I I
RR
R
I
21
1
2
Kirchhoff's Current and Voltage Laws
In case of parallel : 1 2
1 2
1 1 1
, , V=
I I
G G G
R R R R G

11.  sum of voltages around any loop in a circuit is zero.
KVL
• A voltage encountered + to - is positive.
• A voltage encountered - to + is negative.
KVL Mathematically 0)(
1
n
j
j tv 0
1
n
j
jV
Kirchhoff's Current and Voltage Laws

12. KVL
Determine the voltages Vae and Vec.
Kirchhoff's Current and Voltage Laws
10 24 0ae
V
16 12 4 6 0ae
V
4 + 6 + Vec = 0

13. KVL
Voltage divider
R1
R2
-
V1
+
+
-
V2
+
-
V
21
1
11
RR
R
VIRV
21
2
22
RR
R
VIRV
Important voltage Divider
equations
N
Kirchhoff's Current and Voltage Laws

14. KVL
Voltage divider
kR 151
Volume control?
Example: Vs = 9V, R1 = 90kΩ, R2 = 30kΩ
Kirchhoff's Current and Voltage Laws

15. Mesh Analysis
• Technique to find voltage drops around a
loop using the currents that flow within the
loop, Kirchoff’s Voltage Law, and Ohm’s Law
– First result is the calculation of the mesh currents
• Which can be used to calculate the current flowing
through each component
– Second result is a calculation of the voltages
across the components
• Which can be used to calculate the voltage at the
nodes.

16. Mesh Analysis
 What is a mesh:
 It is a loop which does not
contain any other loops
within it.
i1
i2
This circuit
has two
meshes

17. Steps in Mesh Analysis
Vin

18. Step 1
• Identify all of the meshes in the circuit
Vin

19. Step 2
• Label the currents flowing in each mesh
i1
i2
Vin

20. Step 3
• Label the voltage across each component in
the circuit
i1
i2
+
V1
_
Vin
+
V3
_
+
V5
_
+
V6
_
+ V2 - + V4 -

21. Step 4
• Use Kirchoff’s Voltage Law
i1
i2
+
V1
_
Vin
+
V3
_
+
V5
_
+
V6
_
+ V2 - + V4 -
0
0
543
6321
VVV
VVVVVin

22. Step 5
• Use Ohm’s Law to relate the voltage drops
across each component to the sum of the
currents flowing through them.
– Follow the sign convention on the resistor’s voltage.
RIIV baR

23. Step 5
i1
i2
+
V1
_
Vin
+
V3
_
+
V5
_
+
V6
_
+ V2 - + V4 -
616
525
424
3213
212
111
RiV
RiV
RiV
RiiV
RiV
RiV

24. Step 6
• Solve for the mesh currents, i1 and i2
– These currents are related to the currents found
during the nodal analysis.
213
542
62171
iiI
IIi
IIIIi

25. Step 7
• Once the mesh currents are known, calculate
the voltage across all of the components.

26. 12V

27. From Previous Slides
616
525
424
3213
212
111
RiV
RiV
RiV
RiiV
RiV
RiV
0
0
543
6321
VVV
VVVVVin

28. Substituting in Numbers
kiV
kiV
kiV
kiiV
kiV
kiV
1
3
6
5
8
4
16
25
24
213
12
11
0
012
543
6321
VVV
VVVVV

29. Substituting the results from Ohm’s
Law into the KVL equations
0365
0158412
2221
12111
kikikii
kikiikikiV

30. Results
• One or more of the mesh currents may have a
negative sign.
Mesh Currents ( A)
i1 740
i2 264

31. Results
Currents ( A)
IR1 = i1 740
IR2 = i1 740
IR3 = i1- i2 476
IR4 = i2 264
IR5 = i2 264
IR6 = i1 740
IVin = i1 740
The currents through each component in the
circuit.

32. Example
Using Mesh analysis find the currents
through each resistor
KVL in loop 1:
-2+2i1+4(i1-i2)= 0
6i1-4i2-2= 0
6i1-4i2= 2 …………..1)
KVL in loop 2:
6+4(i2-i1)+i2= 0
-4i1+5i2= -6 ………..2)
From eqn 1)&2)
Loop currents: i1= -1A, i2= -2A
Currents through each resistor:
i2 = i1= -1A
i1 = i2 = -2A
i4 = i1-i2
= -1A-(-2A)
= 1A
i1
i2

33. Example
Use the mesh current method to determine the power
associated with each voltage source in the circuit.
Calculate the voltage vo across the 8 resistor.
KVL in Loop 1:
-40+2i1+8(i1-i2)=0
KVL in Loop 2:
8(i2-i1)+6i2+6(i2-i3)=0
KVL in Loop 3:
6(i3-i2)+4i3+20=0
i1 i2 i3

34. 10i1-8i2+0i3=40
-8i1+20i2-6i3=0
0i1-6i2+10i3= -20
By solving the matrix
i1=5.6A
i2= 2A
i3= -0.8A
P40v= -40i1= -40(5.6) = -224W
P20v = 20i3= 20(-0.8) = -16W
vo= 8(i1-i2)= 8(5.6-2) = 8(3.6)=28.8V

35. 35
Example
Apply KVL to each mesh
2 1 7 5
0s
V v v v
2 6 7
0v v v
15 3
0s
v v v
Mesh 1:
Mesh 2:
Mesh 3:
14 8 6
0s
v v V vMesh 4:
DC
DC
1R
3R
5R
7R
2R
6R
8R
4R
1v 2v
3v 4v
5v 6v
7v
8v
+ +
+ +
+
+
+
+
-
-
- -
-
-
-
-
1sV
2sV 1i 2i
3i 4i

36. 36
DC
DC
1R
3R
5R
7R
2R
6R
8R
4R
1v 2v
3v 4v
5v 6v
7v
8v
+ +
+ +
+
+
+
+
-
-
- -
-
-
-
-
1sV
2sV 1i 2i
3i 4i
2 1 7 5
0s
V v v v
2 6 7
0v v v
15 3
0s
v v v
Mesh 1:
Mesh 2:
Mesh 3:
14 8 6
0s
v v V vMesh 4:
2 1 1 1 2 7 1 3 5
( ) ( ) 0s
V i R i i R i i R
2 2 2 4 6 2 1 7
( ) ( ) 0i R i i R i i R
13 1 5 3 3
( ) 0s
i i R V i R
Mesh 1:
Mesh 2:
Mesh 3:
14 4 4 8 4 2 6
( ) 0s
i R i R V i i RMesh 4:
Express the voltage in terms of the mesh
currents:

37. 37
2 1 1 1 2 7 1 3 5
( ) ( ) 0s
V i R i i R i i R
2 2 2 4 6 2 1 7
( ) ( ) 0i R i i R i i R
13 1 5 3 3
( ) 0s
i i R V i R
Mesh 1:
Mesh 2:
Mesh 3:
14 4 4 8 4 2 6
( ) 0s
i R i R V i i RMesh 4:
Mesh 1:
Mesh 2:
Mesh 3:
Mesh 4:
21 5 7 1 7 2 5 3
( ) s
R R R i R i R i V
7 1 2 6 7 2 6 4
( ) 0R i R R R i R i
15 1 3 5 3
( ) s
R i R R i V
16 2 4 6 8 4
( ) s
R i R R R i V

38. 38
Mesh 1:
Mesh 2:
Mesh 3:
Mesh 4:
21 5 7 1 7 2 5 3
( ) s
R R R i R i R i V
7 1 2 6 7 2 6 4
( ) 0R i R R R i R i
15 1 3 5 3
( ) s
R i R R i V
16 2 4 6 8 4
( ) s
R i R R R i V
2
1
1
1 5 7 7 5 1
7 2 6 7 6 2
5 3 5 3
6 4 6 8 4
0
00
0 0
0 0
s
s
s
VR R R R R i
R R R R R i
VR R R i
R R R R i V