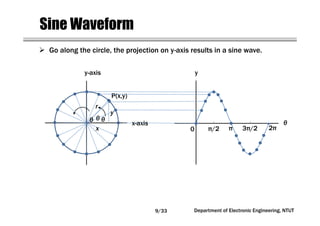
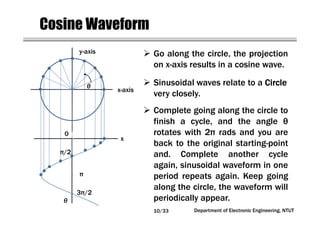
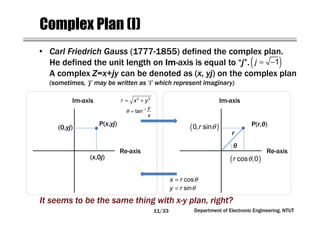
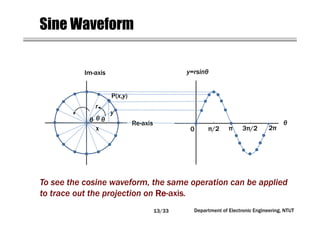
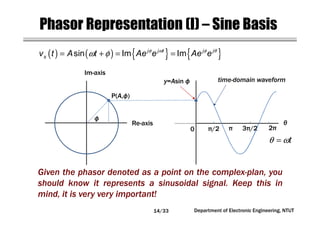
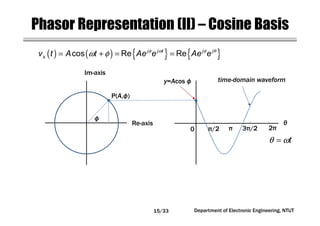
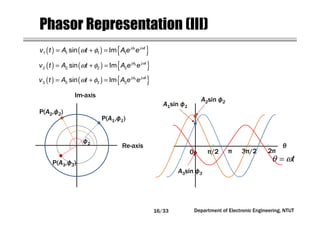
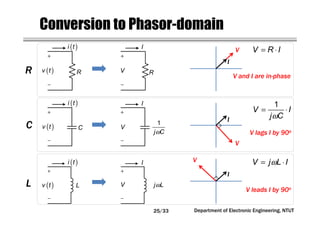
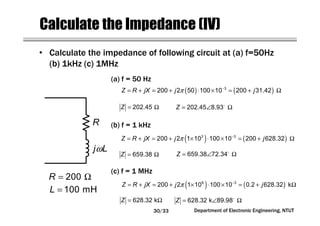
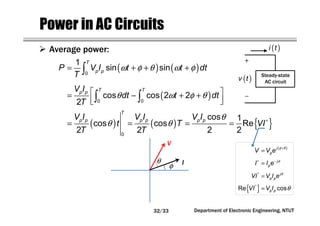
This document covers concepts related to phasors, complex numbers, and sinusoidal steady-state analysis in electrical engineering. It includes mathematical definitions such as compound interest, logarithms, and representations of sinusoidal functions in phasor form. Additionally, the document discusses the relationship between sine and cosine waveforms and their representation in both time and phasor domains.

1. Network Analysis
Chapter 2 e, Phasor, and
Sinusoidal Steady-State Analysis
Chien-Jung Li
Department of Electronic Engineering
National Taipei University of Technology

2. Department of Electronic Engineering, NTUT
Compound Interest
• 複利公式: 本金P, 年利率r, 一年複利n次,
t年後本金加利息之總和為
 
= + 
 
1
nt
r
S P
n
• Let P=1, r=1, and t=1
 
= + 
 
1
1
n
S
n
When n goes to infinite, S converges to 2.718… (= e)
Let P=10萬, r/n=10%/12, t=1 S=11,0471
Let P=10萬, r/n=10%, and n=36, t=1 S=3,091,268
2/33

3. Department of Electronic Engineering, NTUT
Development of Logarithm
• Michael Stifel (1487-1567)
• John Napier (1550-1617)
• 利用對數而將乘法變成加法的特性，刻卜勒成功
計算了火星繞日的軌道。
( )+
∗ = =
2 52 5 7
m m m m
( )−
= =
7 7 4 3
4
m m m
m
( )− −
= = =
2 2 3 1
3
1m m m
mm
− − −
=⋯ ⋯3 2 1 0 1 2 3
, , , , 1, , , ,m m m m m m m
3/33

4. Department of Electronic Engineering, NTUT
Definition of dB (分貝)
• , where
• Power gain
• Voltage gain
• Power (dBW)
• Power (dBm)
• Voltage (dBV)
• Voltage (dBuV)
( )= ⋅10 logdB G ( )= aG
b
 = ⋅  
 
2
1
10 log
P
P
 = ⋅  
 
2
1
20 log
V
V
( )= ⋅10 log
1-W
P
( )= ⋅10 log
1-mW
P
( )= ⋅20 log
1-Volt
V
( )µ
= ⋅20 log
1- V
V
相對量 ((((比例,,,, 比值,,,, 無單位, dB), dB), dB), dB)
絕對量 ((((因相對於一絕對單位,,,,
因此可表示一絕對量.... 有單位,,,,
單位即為dBWdBWdBWdBW,,,, dBmdBmdBmdBm,,,, dBVdBVdBVdBV…)…)…)…)
4/33

5. Department of Electronic Engineering, NTUT
In some textbooks, phasor may be
represented as
Euler’s Formula
• Euler’s Formula cos sinjx
e x j x= +
( ) ( ) ( )
{ } { }ω φ φ ω
ω φ +
= ⋅ + = ⋅ = ⋅cos Re Re
j t j j t
p p pv t V t V e V e e
φ
φ= ⋅ = ∠
def
j
p pV V e V
• Phasor (相量)
Don’t be confused with VectorVectorVectorVector (向量) which is commonly
denoted as A
(How it comes?)
取實部 (即cosine部分) phasor
A real sinusoidal signal v(t) that can be represented as:
V
V
5/33

6. Department of Electronic Engineering, NTUT
Definition of e
lim 1
n
x
n
x
e
n→∞
 
= + 
 
2 3
lim 1 1
1! 2! 3!
n
x
n
x x x x
e
n→∞
 
= + = + + + + 
 
…
x jx=
( ) ( )
2 3
1
1! 2! 3!
jx jx jxjx
e = + + + +…
• Euler played a trick let , where 1j = −
1
lim 1
n
n
e
n→∞
 
= + 
 
6/33

7. Department of Electronic Engineering, NTUT
• Since , , ,
How It Comes…
1j = − 2
1j = − 3
1j = − − 4
1j =
   
= − + − + + − + − +   
   
… …
2 4 3 5
1
2! 4! 3! 5!
x x x x
j x
2 4
cos 1
2! 4!
x x
x = − + − +…
3 5
sin
3! 5!
x x
x x= − + − +…
cos sinjx
e x j x= +
cos sinjx
e x j x−
= −
cos
2
jx jx
e e
x
−
+
=
−
−
=sin
2
jx jx
e e
x
j
( ) ( )= + + + +…
2 3
1
1! 2! 3!
jx jx jxjx
e
• Use and
we have
(姊妹式)
7/33

8. Department of Electronic Engineering, NTUT
Coordinate Systems
x-axis
y-axis
x-axis
y-axis
P(r,θ)
θ
r
P(x,y)
2 2
r x y= +
1
tan
y
x
θ −
=
cosx r θ=
siny r θ=
Cartesian Coordinate System
(笛卡兒座標系, 直角座標系)
Polar Coordinate System
(極坐標系)
(x,0)
(0,y)
( )cos ,0r θ
( )0, sinr θ
Projection
on x-axis
Projection
on y-axis
8/33

9. Department of Electronic Engineering, NTUT
Sine Waveform
x-axis
y-axis
P(x,y)
x
y
r
θ θθ
y
θ
0 π/2 π 3π/2 2π
Go along the circle, the projection on y-axis results in a sine wave.
9/33

10. Department of Electronic Engineering, NTUT
x
θ
0
π/2
π
3π/2
Cosine Waveform
x-axis
y-axis
θ
Go along the circle, the projection
on x-axis results in a cosine wave.
Sinusoidal waves relate to a CircleCircleCircleCircle
very closely.
Complete going along the circle to
finish a cycle, and the angle θ
rotates with 2π rads and you are
back to the original starting-point
and. Complete another cycle
again, sinusoidal waveform in one
period repeats again. Keep going
along the circle, the waveform will
periodically appear.
10/33

11. Department of Electronic Engineering, NTUT
Complex Plan (I)
It seems to be the same thing with x-y plan, right?
• Carl Friedrich Gauss (1777-1855) defined the complex plan.
He defined the unit length on ImImImIm-axis is equal to “j”.
A complex Z=x+jy can be denoted as (x, yj) on the complex plan.
(sometimes, ‘j’ may be written as ‘i’ which represent imaginary)
Re-axis
Im-axis
Re-axis
Im-axis
P(r,θ)
θ
r
P(x,yj)
2 2
r x y= +
1
tan
y
x
θ −
=
cosx r θ=
siny r θ=
(x,0j)
(0,yj)
( )cos ,0r θ
( )0, sinr θ
( )1j = −
11/33

12. Department of Electronic Engineering, NTUT
Complex Plan (II)
Re-axis
Im-axis
1
Every time you multiply something by j, that thing will rotate
90 degrees.
1j = − 2
1j = − 3
1j = − − 4
1j =
1*j=j
j
j*j=-1
-1
-j
-1*j=-j -j*j=1
(0.5,0.2j)
(-0.2, 0.5j)
(-0.5, -0.2j)
(0.2, -0.5j)
• Multiplying j by j and so on:
12/33

13. Department of Electronic Engineering, NTUT
Sine Waveform
Re-axis
Im-axis
P(x,y)
x
y
r
θ θθ
y=rsinθ
θ
0 π/2 π 3π/2 2π
To see the cosine waveform, the same operation can be applied
to trace out the projection on ReReReRe-axis.
13/33

14. Department of Electronic Engineering, NTUT
Phasor Representation (I) – Sine Basis
( ) ( ) { } { }φ ω φ θ
ω φ= + = =sin Im Imj j t j j
sv t A t Ae e Ae e
Re-axis
Im-axis
P(A,ф)
y=Asin ф
θ
0 π/2 π 3π/2 2π
ф
tθ ω=
Given the phasor denoted as a point on the complex-plan, you
should know it represents a sinusoidal signal. Keep this in
mind, it is very very important!
time-domain waveform
14/33

15. Department of Electronic Engineering, NTUT
Phasor Representation (II) – Cosine Basis
( ) ( ) { } { }φ ω φ θ
ω φ= + = =cos Re Rej j t j j
sv t A t Ae e Ae e
Re-axis
Im-axis
P(A,ф)
y=Acos ф
θ
0 π/2 π 3π/2 2π
ф
tθ ω=
time-domain waveform
15/33

16. Department of Electronic Engineering, NTUT
Phasor Representation (III)
( ) ( ) { }φ ω
ω φ= + = 1
1 1 1 1sin Im j j t
v t A t A e e
Re-axis
Im-axis
P(A1,ф1)
ф1
P(A2,ф2)
P(A3,ф3)
θ
0 π/2 π 3π/2 2π
tθ ω=
A1sin ф1
( ) ( ) { }φ ω
ω φ= + = 2
2 2 2 2sin Im j j t
v t A t A e e
( ) ( ) { }φ ω
ω φ= + = 3
3 3 3 3sin Im j j t
v t A t A e e
A2sin ф2
A3sin ф3
16/33

17. Department of Electronic Engineering, NTUT
Mathematical Operation
j t
j tde
j e
dt
ω
ω
ω= ⋅
1j t j t
e dt e
j
ω ω
ω
= ⋅∫
( ) ( )0
1 t
v t i t dt
C
= ∫
ω
= = ⋅
1
CV I Z I
j C
( )
( )di t
v t L
dt
=
ω= ⋅ = ⋅LV j L I Z I
ω
= =
1 1
CZ
j C sC
ω= =LZ j L sL
• LLLL and CCCC: from time-domain to phasor-domain analysis
(s is the Laplace operator)
( )σ ω σ= + =, here let 0s j
17/33

18. Department of Electronic Engineering, NTUT
Phasor Everywhere
• 電路學、電子學: Phasor 常見為一個固定值 (亦可為變量)
• 電磁學、微波工程: Phasor 常見為變動量, 隨傳播方向變化
• 通訊系統: Phasor 常見為變動量, 隨時間變化
此變動的phasor也經常被稱作複數波包(complex envelope)、波包
(envelope)，或帶通訊號的等效低通訊號(equivalent lowpass signal of
the bandpass signal)。Phasor如果被拆成正交兩成分，常稱作I/Q訊
號，而在數位通訊裡表示I/Q訊號的複數平面(座標系)也被稱為星座
圖(constellation)。
• You will see “Phasor” many times in your E.E. life. It just
appears with different names, and it is just a representation
or an analysis technique.
• Keep in mind that a phasor represents a signal, it’s like a
head on your body.
18/33

19. Department of Electronic Engineering, NTUT
Simple Relation Between Sine and Cosine
• Sine CosineSine CosineSine CosineSine Cosine
π/2 π 3π/2 2π
sinθ
θ
0
cosθ
• Negative sine or cosineNegative sine or cosineNegative sine or cosineNegative sine or cosine
( )θ θ= +cos sin 90
( )θ θ= −sin cos 90
( )θ θ− = +cos cos 180
( )θ θ− = +sin sin 180
Try to transform into sine-form:θ−cos
( ) ( ) ( )θ θ θ θ− = − + = + = −cos sin 90 sin 270 sin 90
19/33

20. Department of Electronic Engineering, NTUT
Cosine as a Basis
( ) { }ω
ω= =cos Re j t
pv t V t Ve
= ∠0pV V
( ) { }ωπ
ω ω
 
= = − = 
 
sin cos Re
2
j t
p pv t V t V t Ve
= ∠ − 90pV V
( ) ( ) { }ω
ω ω π= − = + =cos cos Re j t
p pv t V t V t Ve
= ∠180pV V
( ) { }ωπ
ω ω
 
= − = + = 
 
sin cos Re
2
j t
p pv t V t V t Ve
= ∠90pV V
cosinecosinecosinecosine
sinesinesinesine
negative cosinenegative cosinenegative cosinenegative cosine
negative sinenegative sinenegative sinenegative sine
Phasor
Phasor
Phasor
Phasor
20/33

21. Department of Electronic Engineering, NTUT
Sine as a Basis
( ) { }ω
ω= =sin Im j t
pv t V t Ve
= ∠0pV V
( ) { }ωπ
ω ω
 
= = + = 
 
cos sin Im
2
j t
p pv t V t V t Ve
= ∠90pV V
( ) ( ) { }ω
ω ω π= − = + =sin sin Im j t
p pv t V t V t Ve
= ∠180pV V
( ) { }ωπ
ω ω
 
= − = − = 
 
cos sin Im
2
j t
p pv t V t V t Ve
= ∠ − 90pV V
Phasor
Phasor
Phasor
Phasor
cosinecosinecosinecosine
sinesinesinesine
negative cosinenegative cosinenegative cosinenegative cosine
negative sinenegative sinenegative sinenegative sine
21/33

22. Department of Electronic Engineering, NTUT
Addition of Sinusoidal
A basic property of sinusoidal functions is that the sum of an arbitrary
number of sinusoids of the same frequency is equivalent to a single
sinusoid of the given frequency. It must be emphasized that all sinusoids
must be of the same frequency.
( ) ( )ω θ= +sinpv t V t
θ= ∠1 1 1pV V
θ= ∠2 2 2pV V
θ= ∠n pn nV V
= + + +⋯1 2 nV V V V
( ) ( ) ( ) ( )ω θ ω θ ω θ= + + + + + +⋯1 1 2 2sin sin sinp p pn nv t V t V t V t
( )1v t ( )2v t ( )nv t
22/33

23. Department of Electronic Engineering, NTUT
Example
( ) ( ) ( )= +0 1 2v t v t v t
( ) ( )= −1 20cos 100 120v t t ( ) ( )= − +2 15sin 100 60v t t
= ∠ − = −1 20 30 17.3205 10V j
= ∠ − = − −2 15 120 7.5 12.9904V j
( ) ( )= − + − −0 17.3205 10 7.5 12.9904V j j
( ) ( )= −0 25sin 100 66.87v t t
= − = ∠ −9.8205 22.9904 25 66.87j
= ∠ − = − −1 20 120 10 17.321V j
= ∠ = − +2 15 150 12.9904 7.5V j
( ) ( )= − − + − +0 10 17.321 12.9904 7.5V j j
= − − = ∠22.9904 9.8205 25 203.13j
( ) ( )= +0 25cos 100 203.13v t t
( )= −25sin 100 66.87t
Choose the basis you like, and the results are identical.
andFor
calculate
use sine function as a basis use cosine function as a basis
23/33

24. Department of Electronic Engineering, NTUT
Steady-state Impedance
= = +
V
Z R jX
I
• Steady-state impedance
resistance
reactance
= = +
I
Y G jB
Z
• Steady-state admittance
conductance
susceptance
= +30 40Z j
= Ω30R
= Ω40X
= = −
+
1
0.012 0.016
30 40
Y j
j
= 0.012G S
= −0.016X S
24/33

25. Department of Electronic Engineering, NTUT
Conversion to Phasor-domain
( )i t
( )v t V
I
RR
( )i t
( )v t
( )i t
( )v t
C
L
ω
1
j C
V
I
ωj LV
I
= ⋅V R I
ω
= ⋅
1
V I
j C
ω= ⋅V j L I
V
I
V
I
V
I
V and I are in-phase
V lags I by 90o
V leads I by 90o
R
C
L
25/33

26. Department of Electronic Engineering, NTUT
Frequency Response
Frequency-independent
All pass
Frequency-dependent
High-pass
Frequency-dependent
Low-pass
V
I
R
ω
1
j C
V
I
ωj LV
I
= + =Z R jX R
ω
= + =
1
Z R jX
C
ω π= 2 f
ω π= 2 f
ω π= 2 f
ω= + =Z R jX L
26/33

27. Department of Electronic Engineering, NTUT
Calculate the Impedance (I)
ω
1
j C
V
• Calculate the impedance of a 0.01-uF capacitor at (a) f=50Hz
(b) 1kHz (c) 1MHz
( )π −
= + = + = − Ω
⋅ × 6
1
0 318.309 k
2 50 0.01 10
Z R jX j
j
= − Ω318.309 kX = Ω318.309 kZ
I
(a) f = 50 Hz
( )π −
= + = + = − Ω
× ⋅ ×3 6
1
0 15.92 k
2 1 10 0.01 10
Z R jX j
j
= − Ω15.92 kX = Ω15.92 kZ
(b) f = 1 kHz
( )π −
= + = + = − Ω
× ⋅ ×6 6
1
0 15.92
2 1 10 0.01 10
Z R jX j
j
= − Ω15.92X = Ω15.92Z
(c) f = 1 MHz
= 0.01 µFC
27/33

28. Department of Electronic Engineering, NTUT
Calculate the Impedance (II)
• Calculate the impedance of a 100-mH inductor at (a) f=50Hz
(b) 1kHz (c) 1MHz
( )π −
= + = + ⋅ × = Ω3
0 2 50 100 10 31.42Z R jX j j
= Ω31.42X = Ω31.42Z
(a) f = 50 Hz
( )π −
= + = + × ⋅ × = Ω3 3
0 2 1 10 100 10 628.32Z R jX j j
= Ω628.32X = Ω628.32Z
(b) f = 1 kHz
( )π −
= + = + × ⋅ × = Ω6 3
0 2 1 10 100 10 628.32 kZ R jX j j
= Ω628.32 kX = Ω628.32 kZ
(c) f = 1 MHz
ωj LV
I
= 100 mHL
28/33

29. Department of Electronic Engineering, NTUT
Calculate the Impedance (III)
• Calculate the impedance of following circuit at (a) f=50Hz
(b) 1kHz (c) 1MHz
( )
( )
π −
= + = + = − Ω
⋅ × 6
1
200 0.2 318.309 k
2 50 0.01 10
Z R jX j
j
= Ω318.309 kZ
(a) f = 50 Hz
( )
( )
π −
= + = + = − Ω
× ⋅ ×3 6
1
200 0.2 15.92 k
2 1 10 0.01 10
Z R jX j
j
= Ω15.92 kZ
(b) f = 1 kHz
( )
( )
π −
= + = + = − Ω
× ⋅ ×6 6
1
200 200 15.92
2 1 10 0.01 10
Z R jX j
j
= Ω200.63Z
(c) f = 1 MHz
ω
1
j C
= 0.01 µFC
R
= Ω200R
= ∠ − Ω318.309k 89.96Z
= ∠ − Ω15.92k 89.26Z
= ∠ Ω200.63 -4.55Z
29/33

30. Department of Electronic Engineering, NTUT
Calculate the Impedance (IV)
• Calculate the impedance of following circuit at (a) f=50Hz
(b) 1kHz (c) 1MHz
( ) ( )π −
= + = + ⋅ × = + Ω3
200 2 50 100 10 200 31.42Z R jX j j
= Ω202.45Z
(a) f = 50 Hz
( ) ( )π −
= + = + × ⋅ × = + Ω3 3
200 2 1 10 100 10 200 628.32Z R jX j j
= Ω659.38Z
(b) f = 1 kHz
( ) ( )π −
= + = + × ⋅ × = + Ω6 3
200 2 1 10 100 10 0.2 628.32 kZ R jX j j
= Ω628.32 kZ
(c) f = 1 MHz
ωj L
= 100 mHL
R
= Ω200R
= ∠ Ω202.45 8.93Z
= ∠ Ω659.38 72.34Z
= ∠ Ω628.32 k 89.98Z
30/33

31. Department of Electronic Engineering, NTUT
Power in AC Circuits
( ) ( )ω φ= +sinpi t I t
( ) ( )ω φ θ= + +sinpv t V t
Instantaneous power absorbed by the circuit:
( ) ( ) ( ) ( ) ( )ω φ θ ω φ= = + + +sin sinp pp t v t i t V I t t
( ) ( ) ( )= =∫ ∫0 0
1 1T T
P p t dt v t i t dt
T T
Average power:
( ) ( )= − − +
1 1
sin sin cos cos
2 2
A B A B A B
Steady-state
AC circuit
( )i t
( )v t
( ) ( )ω φ θ ω φ= + + +∫0
1
sin sin
T
p pV I t t dt
T
31/33

32. Department of Electronic Engineering, NTUT
Power in AC Circuits
Average power:
( )θ ω φ θ = − + +
  ∫ ∫0 0
cos cos 2 2
2
T Tp pV I
dt t dt
T
( ) ( ) { }
θ
θ θ ∗
= = = =
0
cos 1
cos cos Re
2 2 2 2
T
p p p p p pV I V I V I
t T VI
T T
Steady-state
AC circuit
( )i t
( )v t
( ) ( )ω φ θ ω φ= + + +∫0
1
sin sin
T
p pP V I t t dt
T
V
Iθ
φ
( )φ θ+
=
j
pV V e
φ∗ −
= j
pI I e
θ
=* j
p pVI V I e
{ } θ=*
Re cosp pVI V I
32/33

33. Department of Electronic Engineering, NTUT
Root-Mean-Square (RMS) Value
θ
θ θ= = =
cos
cos cos
22 2
p p p p
rms rms
V I V I
P V I
(RMS value is also called the effective value)
When the circuit contains L and C, the current and voltage may not be
in-phase (they can be in-phase if effects of L and C cancelled at the given frequency),
and hence the apparent power may not be totally absorbed by the circuit.
Define RMS voltage and current as
=
2
p
rms
V
V =
2
p
rms
I
I
power factor (PF)
is define as the power factor (功率因子/因素)θ≤ ≤0 cos 1
×Actual power = Apparent power Power factor
θ= cosrms rmsV I
33/33