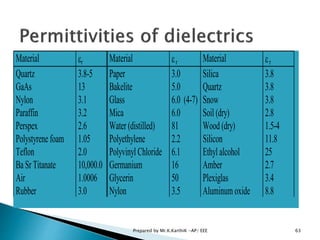
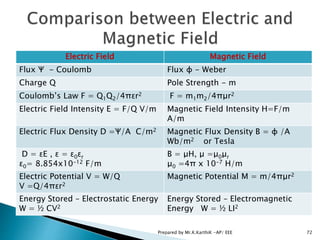
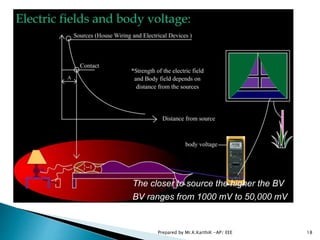
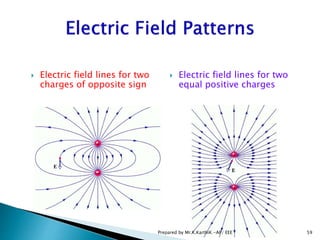
This document contains lecture notes on electromagnetic fields and electrostatics. It begins with introductions to electromagnetic fields, their sources and effects. It then covers topics like coordinate systems, divergence and curl operations, and theorems. The document focuses on electrostatics, defining concepts like the electric field, Coulomb's law, electric potential and capacitance. It provides equations and examples for calculating fields and potentials from different charge distributions. The summary concludes with overviews of conservative fields and the relationship between potential differences and work.























































![ Capacitance: the ratio between
charge and potential of a body
Measured in coulombs/volt. This
unit is called the farad [F].
Capacitance is only defined for two
conducting bodies, across which the
potential difference is connected.
C =
Q
V
C
V
60Prepared by Mr.K.KarthiK -AP/ EEE](https://image.slidesharecdn.com/unit-iii-190203112940/85/ELECTROMAGNETIC-FIELD-60-320.jpg)