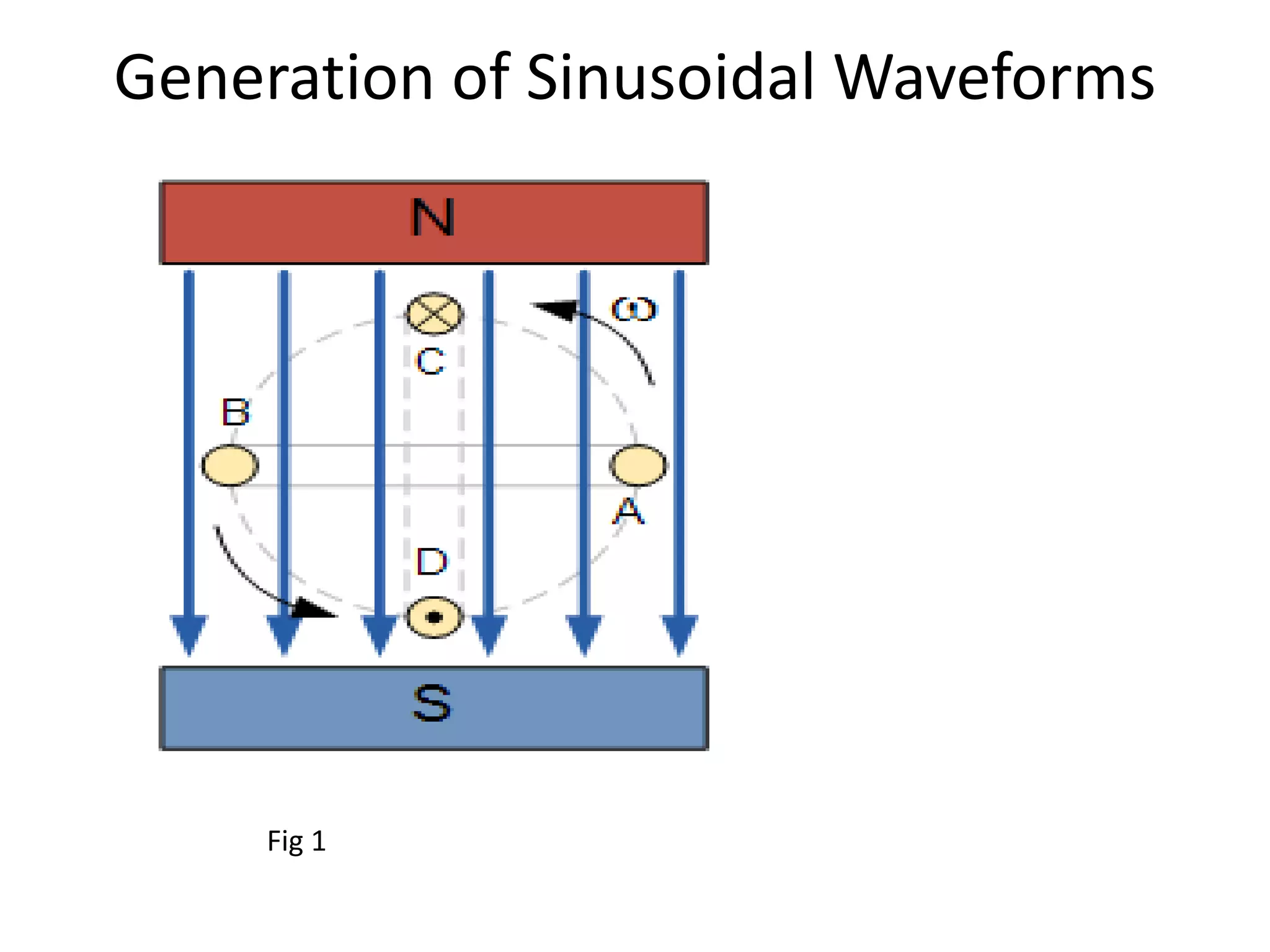
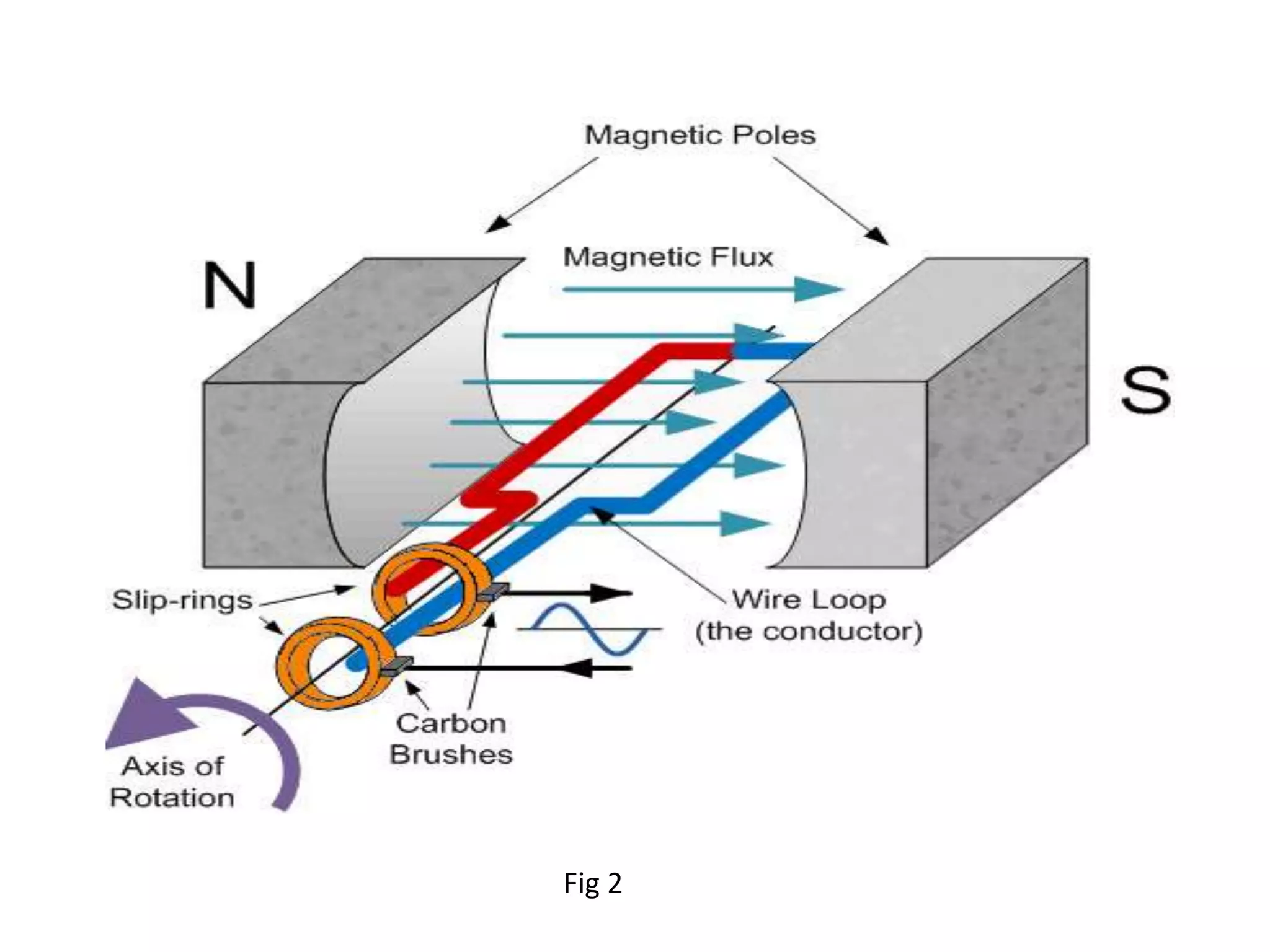
This document provides information about AC circuit analysis including: 1) AC current periodically reverses direction while DC flows in one direction. AC power is delivered to homes and businesses as a sine wave. 2) A simple generator consists of a coil rotating in a magnetic field, inducing a sinusoidal waveform. One cycle is produced per coil revolution. 3) The frequency of an AC generator output depends on the coil rotation speed and number of magnetic pole pairs. Higher speeds or more pole pairs increases frequency.

1. AC circuit analysis
Course: Diploma
Subject: Basics of Electrical Engineering
Unit: 2

2. AC circuit
• In alternating current (AC, also ac), the flow of electric
charge periodically reverses direction. In direct
current (DC, alsodc), the flow of electric charge is only
in one direction. The abbreviations AC and DC are often
used to mean simply alternating and direct, as when
they modify current or voltage.
• AC is the form in which electric power is delivered to
businesses and residences. The usual waveform of
an AC power circuit is a sine wave. In certain
applications, different waveforms are used, such
as triangular or square waves. Audio and radio signals
carried on electrical wires are also examples of
alternating current. In these applications, an important
goal is often the recovery of information encoded
(or modulated) onto the AC signal.

3. Generation of Sinusoidal Waveforms
Fig 1

4. Cont..
• However, if the conductor moves in parallel with the
magnetic field in the case of points A and B, no lines of
flux are cut and no EMF is induced into the conductor,
but if the conductor moves at right angles to the
magnetic field as in the case of points C and D, the
maximum amount of magnetic flux is cut producing the
maximum amount of induced EMF.
• Also, as the conductor cuts the magnetic field at
different angles between points A and C, 0 and 90o the
amount of induced EMF will lie somewhere between
this zero and maximum value. Then the amount of emf
induced within a conductor depends on the angle
between the conductor and the magnetic flux as well
as the strength of the magnetic field.

5. Cont..
• to convert a mechanical energy such as
rotation, into electrical energy, a Sinusoidal
Waveform. A simple generator consists of a pair of
permanent magnets producing a fixed magnetic
field between a north and a south pole. Inside this
magnetic field is a single rectangular loop of wire
that can be rotated around a fixed axis allowing it to
cut the magnetic flux at various angles as shown
below.

6. Fig 2

7. Cont..
• As the coil rotates anticlockwise around the central axis which
is perpendicular to the magnetic field, the wire loop cuts the
lines of magnetic force set up between the north and south
poles at different angles as the loop rotates. The amount of
induced EMF in the loop at any instant of time is proportional
to the angle of rotation of the wire loop.
• As this wire loop rotates, electrons in the wire flow in one
direction around the loop. Now when the wire loop has
rotated past the 180o point and moves across the magnetic
lines of force in the opposite direction, the electrons in the
wire loop change and flow in the opposite direction. Then the
direction of the electron movement determines the polarity
of the induced voltage.

8. Cont..
• So we can see that when the loop or coil physically rotates
one complete revolution, or 360o, one full sinusoidal
waveform is produced with one cycle of the waveform
being produced for each revolution of the coil. As the coil
rotates within the magnetic field, the electrical connections
are made to the coil by means of carbon brushes and slip-
rings which are used to transfer the electrical current
induced in the coil.
• The amount of EMF induced into a coil cutting the magnetic
lines of force is determined by the following three factors.
• • Speed – the speed at which the coil rotates inside the
magnetic field.
• • Strength – the strength of the magnetic field.
• • Length – the length of the coil or conductor passing
through the magnetic field.

9. Cont..
• We know that the frequency of a supply is the
number of times a cycle appears in one second
and that frequency is measured in Hertz. As one
cycle of induced emf is produced each full
revolution of the coil through a magnetic field
comprising of a north and south pole as shown
above, if the coil rotates at a constant speed a
constant number of cycles will be produced per
second giving a constant frequency. So by
increasing the speed of rotation of the coil the
frequency will also be increased. Therefore,
frequency is proportional to the speed of
rotation, ( ƒ ∝ Ν ) where Ν = r.p.m.

10. Cont..
• Also, our simple single coil generator above only
has two poles, one north and one south pole,
giving just one pair of poles. If we add more
magnetic poles to the generator above so that it
now has four poles in total, two north and two
south, then for each revolution of the coil two
cycles will be produced for the same rotational
speed. Therefore, frequency is proportional to
the number of pairs of magnetic poles, ( ƒ ∝ P ) of
the generator where P = is the number of “pairs
of poles”.
• Then from these two facts we can say that the
frequency output from an AC generator is:

11. Cont..

12. Instataneous voltage.
• The EMF induced in the coil at any instant of time
depends upon the rate or speed at which the coil
cuts the lines of magnetic flux between the poles
and this is dependant upon the angle of rotation,
Theta ( θ ) of the generating device. Because an AC
waveform is constantly changing its value or
amplitude, the waveform at any instant in time will
have a different value from its next instant in time.
• For example, the value at 1ms will be different to the
value at 1.2ms and so on. These values are known
generally as the Instantaneous Values, or Vi Then
the instantaneous value of the waveform and also its
direction will vary according to the position of the
coil within the magnetic field as shown below.

13. Cont..
• The instantaneous values of a sinusoidal waveform is
given as the “Instantaneous value = Maximum value
x sin θ ” and this is generalized by the formula.
• Where, Vmax is the maximum voltage induced in the coil
and θ = ωt, is the angle of coil rotation.
• If we know the maximum or peak value of the waveform,
by using the formula above the instantaneous values at
various points along the waveform can be calculated. By
plotting these values out onto graph paper, a sinusoidal
waveform shape can be constructed. In order to keep
things simple we will plot the instantaneous values for the
sinusoidal waveform at every 45o and assume a maximum
value of 100V.

14. AC circuits -- Impedance
• Impedance and Ohm’s Law for AC:
– Impedance is Z = R + jX,
where j = -1, and X is the reactance in [].
– Ohm’s AC Law in s domain: v = i Z
• Resistance R dissipates power as heat.
• Reactance X stores and returns power.
– Inductors have positive reactance Xl=L
– Capacitors have negative reactance Xc=-1/C

15. References - images
• https://www.google.co.in/url?sa=i&rct=j&q=&esrc
=s&source=images&cd=&cad=rja&uact=8&ved=&u
rl=http%3A%2F%2Fwww.electronics-
tutorials.ws%2Faccircuits%2Fsinusoidal-
waveform.html&ei=Xq2bVOyNGIWxuASk_ILACQ&
bvm=bv.82001339,d.c2E&psig=AFQjCNEmQNVeHh
cQI3ofxuGa6PnRVhBlyQ&ust=1419575026116287
• https://www.google.co.in/url?sa=i&rct=j&q=&esrc
=s&source=images&cd=&cad=rja&uact=8&ved=0C
AcQjRw&url=http%3A%2F%2Fwww.slideshare.net
%2Ftaliacarbis%2F141-generation-
sinusoidal&ei=g6-
bVNXdHo6QuAS6t4H4CQ&bvm=bv.82001339,d.c2
E&psig=AFQjCNFRVhj5GK9pEORBUZiCACQIH55wS
w&ust=1419575529000462

16. REFERENCE
• B.L.Theraja, “Electrical Technology Vol.1”, S.Chand
Publication.
• D.P.Kothari, “Basic Electrical Engineering”, Tata
McGraw-Hill publication.
WWW.SCRIBD.COM