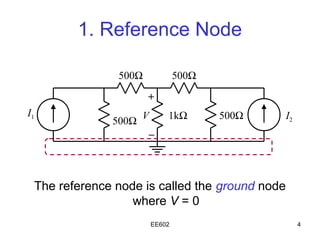
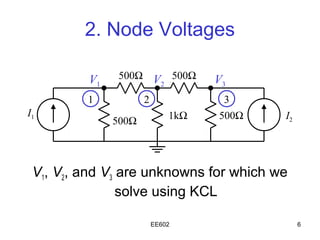
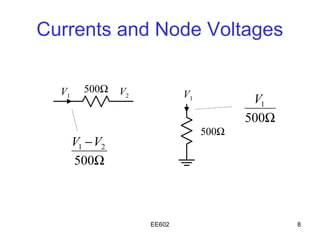
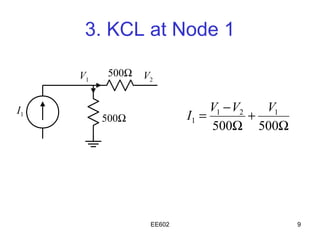
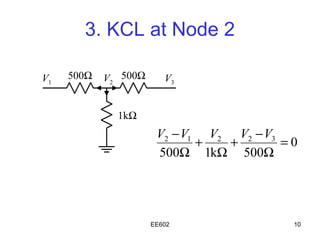
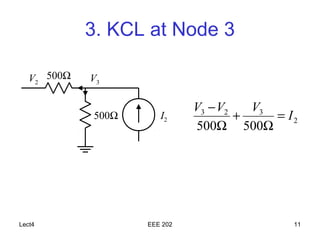
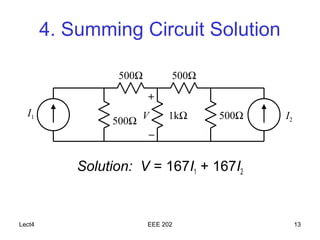
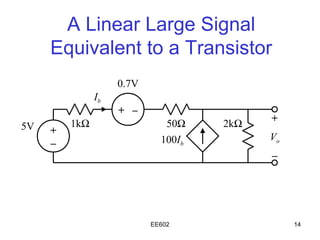
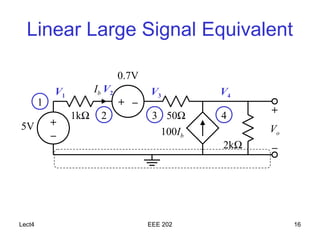
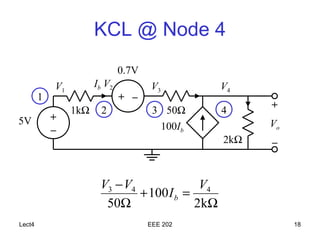
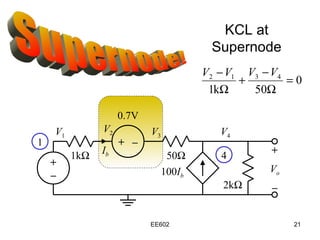
The document discusses the steps of nodal analysis which includes choosing a reference node, assigning voltages to nodes, applying Kirchhoff's Current Law (KCL) at each node to obtain equations relating currents and voltages, and solving the system of equations to determine node voltages. An example circuit is presented and nodal analysis is performed on it by defining node voltages, writing KCL equations, and solving to find the output voltage. Nodal analysis is a technique for analyzing electrical circuits by writing equations at nodes based on KCL.

1. Nodal Analysis
EE602 1

2. Steps of Nodal Analysis
1. Choose a reference (ground) node.
2. Assign node voltages to the other nodes.
3. Apply KCL to each node other than the
reference node; express currents in terms
of node voltages.
4. Solve the resulting system of linear
equations for the nodal voltages.
L EE602 2

3. Example: A Summing Circuit
• The output voltage V of this circuit is
proportional to the sum of the two input
currents I1 and I2
• This circuit could be useful in audio
applications or in instrumentation
• The output of this circuit would probably
be connected to an amplifier
EE602 3

4. 1. Reference Node
500Ω 500Ω
+
I1
500Ω V 1kΩ 500Ω I2
–
The reference node is called the ground node
where V = 0
EE602 4

5. Steps of Nodal Analysis
1. Choose a reference (ground) node.
2. Assign node voltages to the other
nodes.
3. Apply KCL to each node other than the
reference node; express currents in terms
of node voltages.
4. Solve the resulting system of linear
equations for the nodal voltages.
EE 602 5

6. 2. Node Voltages
V1 500Ω V 500Ω V3
2
1 2 3
I1 1kΩ 500Ω I2
500Ω
V1, V2, and V3 are unknowns for which we
solve using KCL
EE602 6

7. Steps of Nodal Analysis
1. Choose a reference (ground) node.
2. Assign node voltages to the other nodes.
3. Apply KCL to each node other than the
reference node; express currents in
terms of node voltages.
4. Solve the resulting system of linear
equations for the nodal voltages.
EE602 7

8. Currents and Node Voltages
V1 500Ω V2 V1
V1
500Ω
500Ω
V1 − V2
500Ω
EE602 8

9. 3. KCL at Node 1
V1 500Ω V2
I1 V1 − V2 V1
500Ω I1 = +
500Ω 500Ω
EE602 9

10. 3. KCL at Node 2
V1 500Ω V2 500Ω V3
1kΩ
V2 − V1 V2 V2 − V3
+ + =0
500Ω 1kΩ 500Ω
EE602 10

11. 3. KCL at Node 3
V2 500Ω V3
V3 − V2 V3
500Ω I2 + = I2
500Ω 500Ω
Lect4 EEE 202 11

12. Steps of Nodal Analysis
1. Choose a reference (ground) node.
2. Assign node voltages to the other nodes.
3. Apply KCL to each node other than the
reference node; express currents in terms
of node voltages.
4. Solve the resulting system of linear
equations for the nodal voltages.
EE602 12

13. 4. Summing Circuit Solution
500Ω 500Ω
+
I1
500Ω V 1kΩ 500Ω I2
–
Solution: V = 167I1 + 167I2
Lect4 EEE 202 13

14. A Linear Large Signal
Equivalent to a Transistor
0.7V
Ib
+ –
+
5V 1kΩ 50Ω 2kΩ
+
100Ib Vo
–
–
EE602 14

15. Steps of Nodal Analysis
1. Choose a reference (ground) node.
2. Assign node voltages to the other nodes.
3. Apply KCL to each node other than the
reference node; express currents in terms
of node voltages.
4. Solve the resulting system of linear
equations for the nodal voltages.
EE602 15

16. Linear Large Signal Equivalent
0.7V
V1 Ib V 2 V3 V4
1 + –
2 3 50Ω 4 +
1kΩ
5V +
100Ib Vo
–
2kΩ –
Lect4 EEE 202 16

17. Steps of Nodal Analysis
1. Choose a reference (ground) node.
2. Assign node voltages to the other nodes.
3. Apply KCL to each node other than the
reference node; express currents in terms
of node voltages.
4. Solve the resulting system of linear
equations for the nodal voltages.
EE602 17

18. KCL @ Node 4
0.7V
V1 Ib V2 V3 V4
1 + –
2 3 50Ω 4 +
1kΩ
5V +
100Ib Vo
–
2kΩ –
V3 − V4 V4
+ 100 I b =
50Ω 2 kΩ
Lect4 EEE 202 18

19. The Dependent Source
• We must express Ib in terms of the node
voltages:
V1 − V2
Ib =
1 kΩ
• Equation from Node 4 becomes
V3 − V4 V1 − V2 V4
+ 100 − =0
50Ω 1 kΩ 2kΩ
EE602 19

20. How to Proceed?
• The 0.7-V voltage supply makes it
impossible to apply KCL to nodes 2 and 3,
since we don’t know what current is
passing through the supply
• We do know that
V2 – V3 = 0.7 V
• The above is a needed constraint
equation
EE602 20

21. KCL at
Supernode
V2 − V1 V3 − V4
+ =0
1kΩ 50Ω
0.7V
V1 V2 V3 V4
1 + –
Ib 4 +
1kΩ 50Ω
+
100Ib Vo
–
2kΩ –
EE602 21