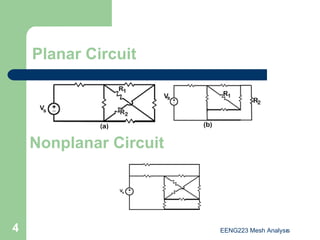
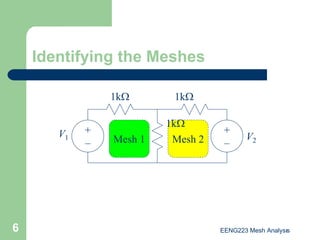
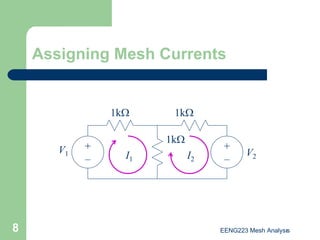
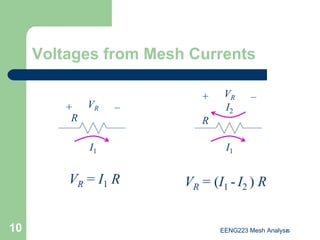
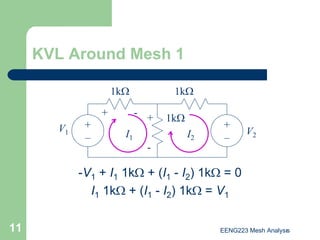
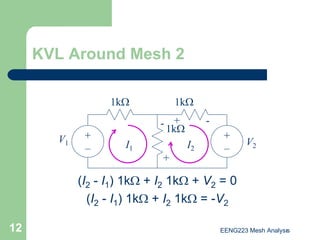
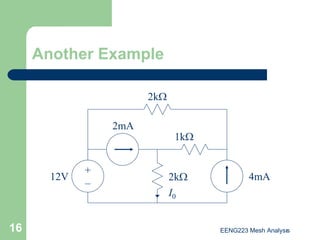
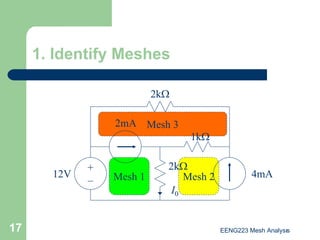
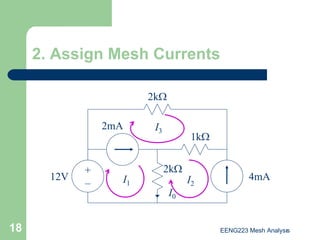
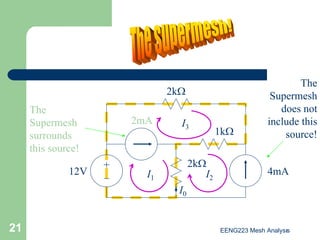
The document discusses the technique of mesh analysis for solving circuits. It begins by defining mesh analysis as applying Kirchhoff's voltage law around loops in a circuit to obtain equations relating loop currents. It then outlines the steps of mesh analysis as: 1) identifying meshes, 2) assigning currents to meshes, 3) applying KVL to obtain equations, 4) solving the resulting system of equations. Examples are provided to demonstrate identifying meshes, assigning currents, writing KVL equations, and setting up the matrix equations to solve.

1. EENG223 Mesh Analysıs
1
Mesh Analysis
Dr. M. K. Uyguroglu

2. EENG223 Mesh Analysıs
2
Mesh Analysis
z Nodal analysis was developed by applying
KCL at each non-reference node.
z Mesh analysis is developed by applying KVL
around meshes/loops in the circuit.
z Mesh analysis results in a system of linear
equations which must be solved for unknown
currents.

3. EENG223 Mesh Analysıs
3
Mesh Analysis
z quantity of interest is current
z a mesh is a loop that does not contain
another loop within it
z work for planar circuit only
planar circuit -> no branch passes over or
under other branch
z M-meshes -> assign clockwise current for
each mesh
z apply KVL around each mesh

4. EENG223 Mesh Analysıs
4
Planar Circuit
Nonplanar Circuit

5. EENG223 Mesh Analysıs
5
Steps of Mesh Analysis
1. Identify meshes.
2. Assign a current to each mesh.
3. Apply KVL around each loop to get an
equation in terms of the loop currents.
4. Solve the resulting system of linear
equations.

6. EENG223 Mesh Analysıs
6
Identifying the Meshes
Mesh 2
1kΩ
1kΩ
1kΩ
V1 V2
Mesh 1
+
–
+
–

7. EENG223 Mesh Analysıs
7
Steps of Mesh Analysis
1. Identify mesh (loops).
2. Assign a current to each mesh.
3. Apply KVL around each loop to get an
equation in terms of the loop currents.
4. Solve the resulting system of linear
equations.

8. EENG223 Mesh Analysıs
8
Assigning Mesh Currents
1kΩ
1kΩ
1kΩ
V1 V2
I1 I2
+
–
+
–

9. EENG223 Mesh Analysıs
9
Steps of Mesh Analysis
1. Identify mesh (loops).
2. Assign a current to each mesh.
3. Apply KVL around each loop to get an
equation in terms of the loop currents.
4. Solve the resulting system of linear
equations.

10. EENG223 Mesh Analysıs
10
Voltages from Mesh Currents
R
I1
+ –
VR
VR = I1 R
R
I1
+ –
VR
I2
VR = (I1 - I2 ) R

11. EENG223 Mesh Analysıs
11
KVL Around Mesh 1
1kΩ
1kΩ
1kΩ
V1 V2
I1 I2
+
–
+
–
+ -
+
-
-V1 + I1 1kΩ + (I1 - I2) 1kΩ = 0
I1 1kΩ + (I1 - I2) 1kΩ = V1

12. EENG223 Mesh Analysıs
12
KVL Around Mesh 2
1kΩ
1kΩ
1kΩ
V1 V2
I1 I2
+
–
+
–
-
-
+
+
(I2 - I1) 1kΩ + I2 1kΩ + V2 = 0
(I2 - I1) 1kΩ + I2 1kΩ = -V2

13. EENG223 Mesh Analysıs
13
Steps of Mesh Analysis
1. Identify mesh (loops).
2. Assign a current to each mesh.
3. Apply KVL around each loop to get an
equation in terms of the loop currents.
4. Solve the resulting system of linear
equations.

14. EENG223 Mesh Analysıs
14
Matrix Notation
z The two equations can be combined into a
single matrix/vector equation.






−
=












Ω
+
Ω
Ω
−
Ω
−
Ω
+
Ω
2
1
2
1
k
1
k
1
k
1
k
1
k
1
k
1
V
V
I
I

15. EENG223 Mesh Analysıs
15
Solving the Equations
Let: V1 = 7V and V2 = 4V
Results:
I1 = 3.33 mA
I2 = -0.33 mA
Finally
Vout = (I1 - I2) 1kΩ = 3.66V

16. EENG223 Mesh Analysıs
16
Another Example
1kΩ
2kΩ
2kΩ
12V 4mA
2mA
I0
+
–

17. EENG223 Mesh Analysıs
17
1. Identify Meshes
Mesh 2
Mesh 3
Mesh 1
1kΩ
2kΩ
2kΩ
12V 4mA
2mA
I0
+
–

18. EENG223 Mesh Analysıs
18
2. Assign Mesh Currents
I1 I2
I3
1kΩ
2kΩ
2kΩ
12V 4mA
2mA
I0
+
–

19. EENG223 Mesh Analysıs
19
Current Sources
z The current sources in this circuit will have
whatever voltage is necessary to make the
current correct.
z We can’t use KVL around the loop because
we don’t know the voltage.
z What to do?

20. EEE 223 Mesh Analysıs
20
Current Sources
z The 4mA current source sets I2:
I2 = -4 mA
z The 2mA current source sets a constraint on
I1 and I3:
I1 - I3 = 2 mA
z We have two equations and three unknowns.
Where is the third equation?

21. EENG223 Mesh Analysıs
21
1kΩ
2kΩ
2kΩ
12V 4mA
2mA
I0
I1 I2
I3
The
Supermesh
surrounds
this source!
The
Supermesh
does not
include this
source!
+
–

22. EENG223 Mesh Analysıs
22
KVL Around the Supermesh
-12V + I3 2kΩ + (I3 - I2)1kΩ + (I1 - I2)2kΩ = 0
I3 2kΩ + (I3 - I2)1kΩ + (I1 - I2)2kΩ = 12V

23. EENG223 Mesh Analysı s
23
Matrix Notation
z The three equations can be combined into a
single matrix/vector equation.









−
=




















Ω
+
Ω
Ω
−
Ω
−
Ω
−
V
12
mA
2
mA
4
1k
2k
2k
1k
2k
1
0
1
0
1
0
3
2
1
I
I
I

24. EENG223 Mesh Analysıs
24
Solve Using MATLAB
>> A = [0 1 0; 1 0 -1;
2e3 -1e3-2e3 2e3+1e3];
>> v = [-4e-3; 2e-3; 12];
>> i = inv(A)*v
i = 0.0012
-0.0040
-0.0008

25. EENG223 Mesh Analysıs
25
Solution
I1 = 1.2 mA
I2 = -4 mA
I3 = -0.8 mA
I0 = I1 - I2 = 5.2 mA

26. EENG223 Mesh Analysıs
26
Class Example