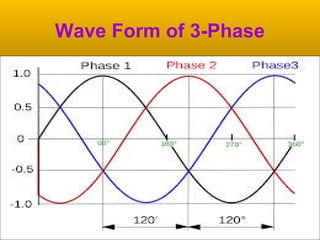
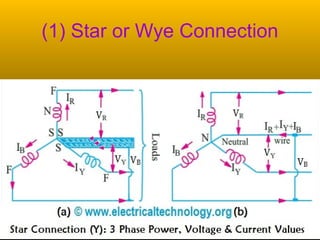
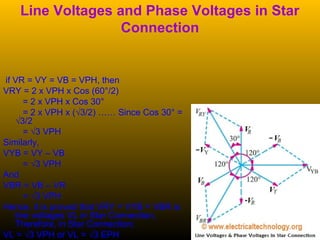
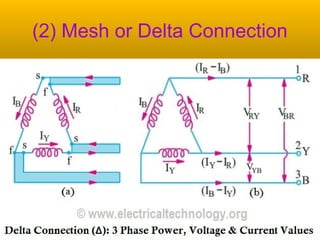
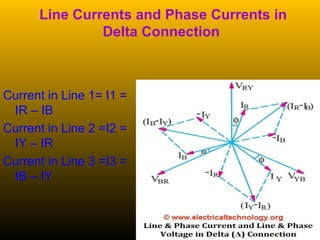
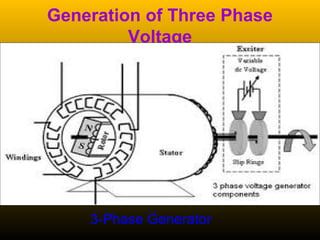
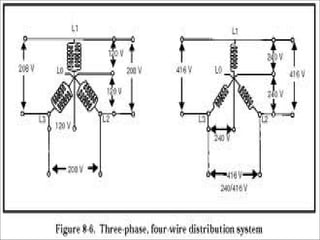
Three-phase systems have multiple voltages or currents that are displaced in time by 120 degrees. They provide advantages over single-phase systems like higher power capacity, self-starting motors, and more constant power output. A 3-phase generator produces 3 voltages displaced by 120 degrees through its winding configuration. The voltages can be connected in either a star or delta configuration. In a star connection, the winding ends meet at a central neutral point. In a delta connection, the windings are connected in a closed loop. 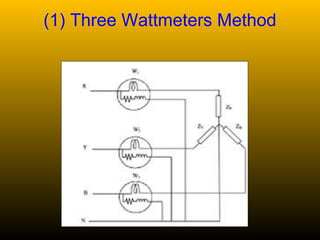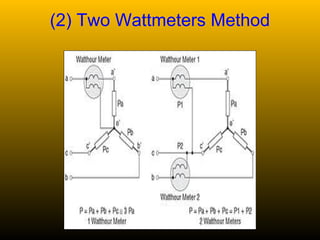Power in a 3-phase circuit can be measured using either 3 wattmeters connected to each phase, or 2 wattmeters connected across different phase combinations to calculate total power.

3. 3-Phase AC Circuit

4. Introduction
Three phase system is a part of a
poly phase system.The different circuits in
polyphase system operate at same
frequency, but their voltage and currents
are out of phase from one other.
In poly phase many number of
phase are displaced from each other with
appropriate angle of electrical degree.

5. Thus, an ac system having a group of
poly phasers having equal voltage & frequency
arregement with equal phase angle difference
between adjacent phases is called a polyphase
system.By considering many advantages of
three phase system over single phase for bulk
power handling, for all practical purpose, three
phase system is universally employed for
generation , transmission& distribution of
electrical power. In addition to that the reason
for immense popularity of three phase appartus
are that (a) more efficiency (b) less material
required for given capicity (c) less cost for
same capacity than single-phase equipment.

6. Agvantages of 3-phase system
over 1-phase
(1)Higher power/weight ratio of alternators.
A three phase alternator is smaller and
lighter that a single phase alternator of the
same power output. Hence, it is also
cheaper.
(2)A three phase transmission system
requires less copper or aluminium to
transmit the same quantity of power of a
specific distance than a single phase
system.

7. (3)Three phase motors are self-starting due to the
rotating magnetic field induced by the three phases.
On the other hand, a single phase motor is not self
starting, it requires a capacitor and an auxilliary
winding.
(4)In Single phase systems, the instanteous
power(power delivered at any instant) is not constant
and is sinusoidal. This results in vibrations in single
phase motors.
In a three phase power system, though, the
instanteous power is always the same.
(5)Three phase motors have better power factor
compared to single phase motors.
(6)Three phase supply can be rectified into dc supply
with a lesser ripple factor

8. Generation of Three Phase
Voltage
3-Phase Generator

10. In 3-phase the armature windings ar displace 120
degree electrical apart. Hence , voltages
induced displacementt between different three
phases. So in general except two-phase
system, electrical displacement between
different phases in 360/n, where n is the
number of phases or windings.In figure 2-poles
& 3-phase stationary armature are shown in
figure.The field winding is on rotating part
known as rotor & armature winding is on
stationary part known as stator of 3-phase a.c.
generator or alternator.

11. It has thre armature coils displaced 120
degree apart from each other.For clock wise
rotation of poles, it is found that the e.m.f.
induced in conductor for coil is maximum when
pole axis lies. The emf is in conductor for coil
would be maximum when the N-S liesss . Thus
we can say , the induced emf is conductor
reaches its maximum value 120 degree later
than the maximum value value in conductor. In
same manner the maximum emf will induced in
conductor , 120 degree later than that or 240
degree later than that in.

12. When the rotor is rotated in clockwise
direction st constant angular velocity w rad/sec,
a sinusoidal voltage is generated across each
coil & thre emf are 120 degree out of phase
with one onother as shown in below wave. As
three coils under 90 with same velocity of field
coil mounted on rotor.Frequency & amplitude of
emfs are equal.

13. Wave Form of 3-Phase

14. Phase Sequence of 3-Phase
System
A three phase system of voltages (or currents) has a
sequence (or order) in which the phases reach a
particular position (for example peak value). This is
the natural sequence of the supply. According to usual
notation, we would call the sequence R-Y-B or A-B-C.
If we consider a balanced system of voltages (or
currents) they will have only the natural sequence, and
there will no other components present. However,
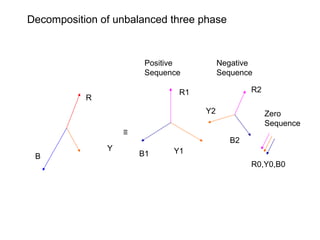
Fortescue has formulated that any unbalanced system
can be split up into a series of balanced systems.
[This is like saying that any force can be broken up
into its components along the x-axis, y-axis and z-axis.
The advantage of such a decomposition is in the
analysis of more than one quantity]

15. In the case of unbalanced three phase system,
such as shown in figure 14, the unbalanced
system can be split up into 3 components: (i) a
balanced system having the same phase
sequence as the unbalanced system, (ii) a
balanced system having the opposite phase
sequence to the unbalanced system (rotation of
phasors is always anticlockwise whether they
are in the same sequence or opposite, so that it
is the order of the phases that changes, and
not the direction of rotation), and (iii) a
balanced system of inphase quantities.

16. R
Y
B
≡
Positive
Sequence
R1
B1 Y1
Negative
Sequence
R2
B2
Y2
Decomposition of unbalanced three phase
R0,Y0,B0
Zero
Sequence

17. In any three phase system, the phase quantities
R, Y and B (or A, B and C) may be
expressed as the phasor sum of:
a set of balanced positive phase sequence
quantities A1, B1 and C1
(phase sequence a-b-c : same phase sequence
as original
unbalanced quantities),
a set of balanced negative phase sequence
currents A2, B2 and C2
(phase sequence a-c-b: opposite phase
sequence to original
unbalanced quantities),a set of identical zero
phase sequence currents A0, B0 and C0

18. Regrouping

19. Interconnection of Three Phase
The interconnection generally made out following
methods:
(1) Star or Wye Connection
(2) Mesh or Delta Connction

20. (1) Star or Wye Connection

21. In this kind of interconnection, the starting ends
or finishing ends (Similar ends) of three coils
are connected together to form the neutral
point. Or
Star Connection is obtained by connecting
together similar ends of the three coils, either
“Starting” or “finishing”. The other ends are
joined to the line wires. The common point is
called the neutral or Star Point, which is
represented by N. (As shown in fig 1)
Star Connection is also called Three Phase 4
wires (3-Phase, 4-Wires) system.

22. Line Voltages and Phase Voltages in Star
Connection
if VR = VY = VB = VPH, then
VRY = 2 x VPH x Cos (60°/2)
= 2 x VPH x Cos 30°
= 2 x VPH x (√3/2) …… Since Cos 30° =
√3/2
= √3 VPH
Similarly,
VYB = VY – VB
= √3 VPH
And
VBR = VB – VR
= √3 VPH
Hence, it is proved that VRY = VYB = VBR is
line voltages VL in Star Connection,
Therefore, in Star Connection;
VL = √3 VPH or VL = √3 EPH

23. (2) Mesh or Delta Connection

24. In this system of interconnection, the starting ends of the
three phases or coils are connected to the finishing
ends of the coil. Or the starting end of the first coil is
connected to the finishing end of the second coil and
so on (for all three coils) and it looks like a closed
mesh or circuit as shown in fig (1).
In more clear words, all three coils are connected in
series to form a close mesh or circuit. Three wires are
taken out from three junctions and the all outgoing
currents from junction assumed to be positive.
In Delta connection, the three windings interconnection
looks like a short circuit, but this is not true, if the
system is balanced, then the value of the algebraic
sum of all voltages around the mesh is zero.
When a terminal is open, then there is no chance of
flowing currents with basic frequency around the
closed mesh.

25. Line Currents and Phase Currents in
Delta Connection
Current in Line 1= I1 =
IR – IB
Current in Line 2 =I2 =
IY – IR
Current in Line 3 =I3 =
IB – IY

26. Masurement of Power In 3-Phase
Circuit
There following methods
(1) Three Wattmeters Method
(2) Two Wattmeters Method

27. (1) Three Wattmeters Method

28. (2) Two Wattmeters Method