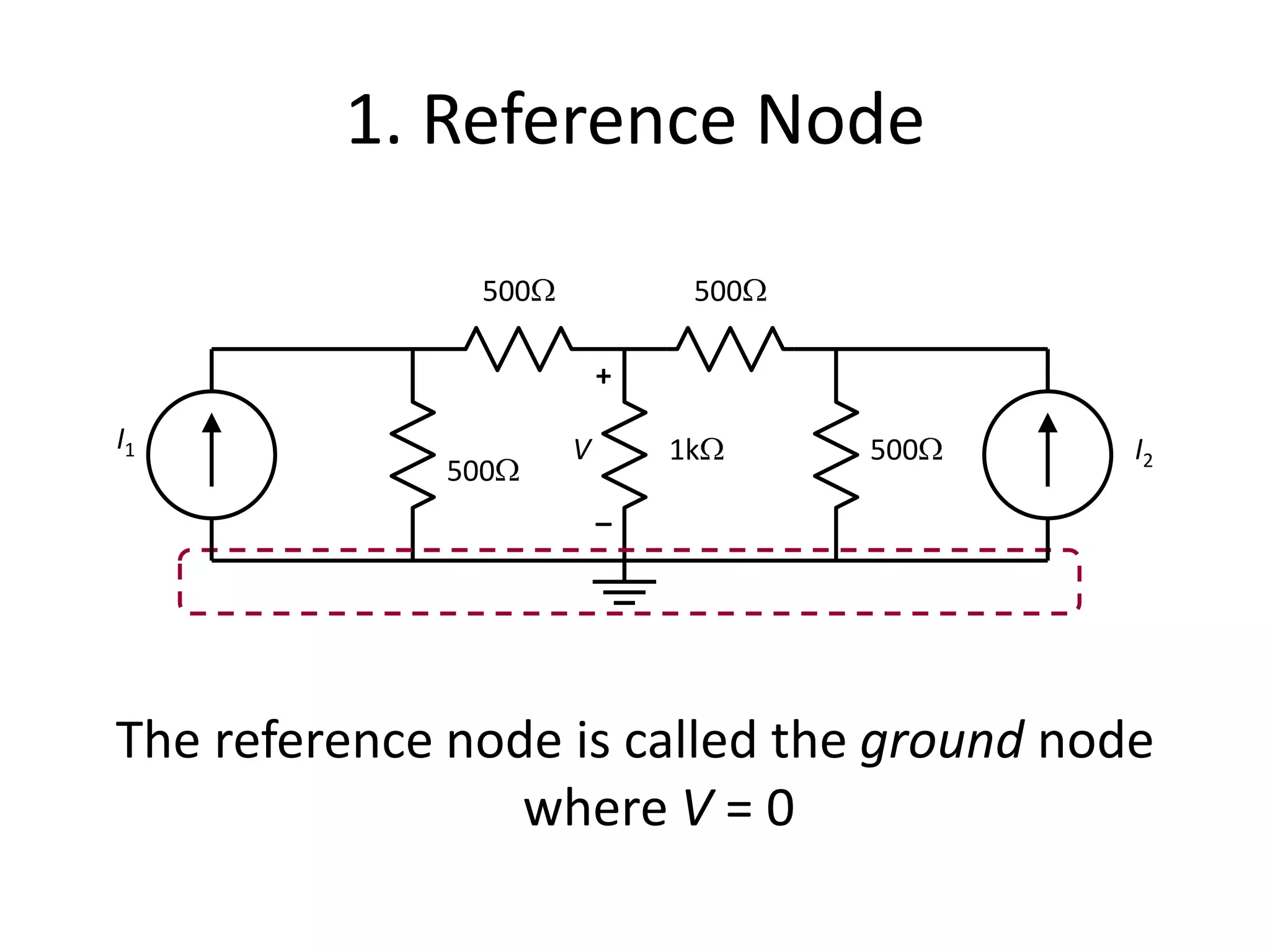
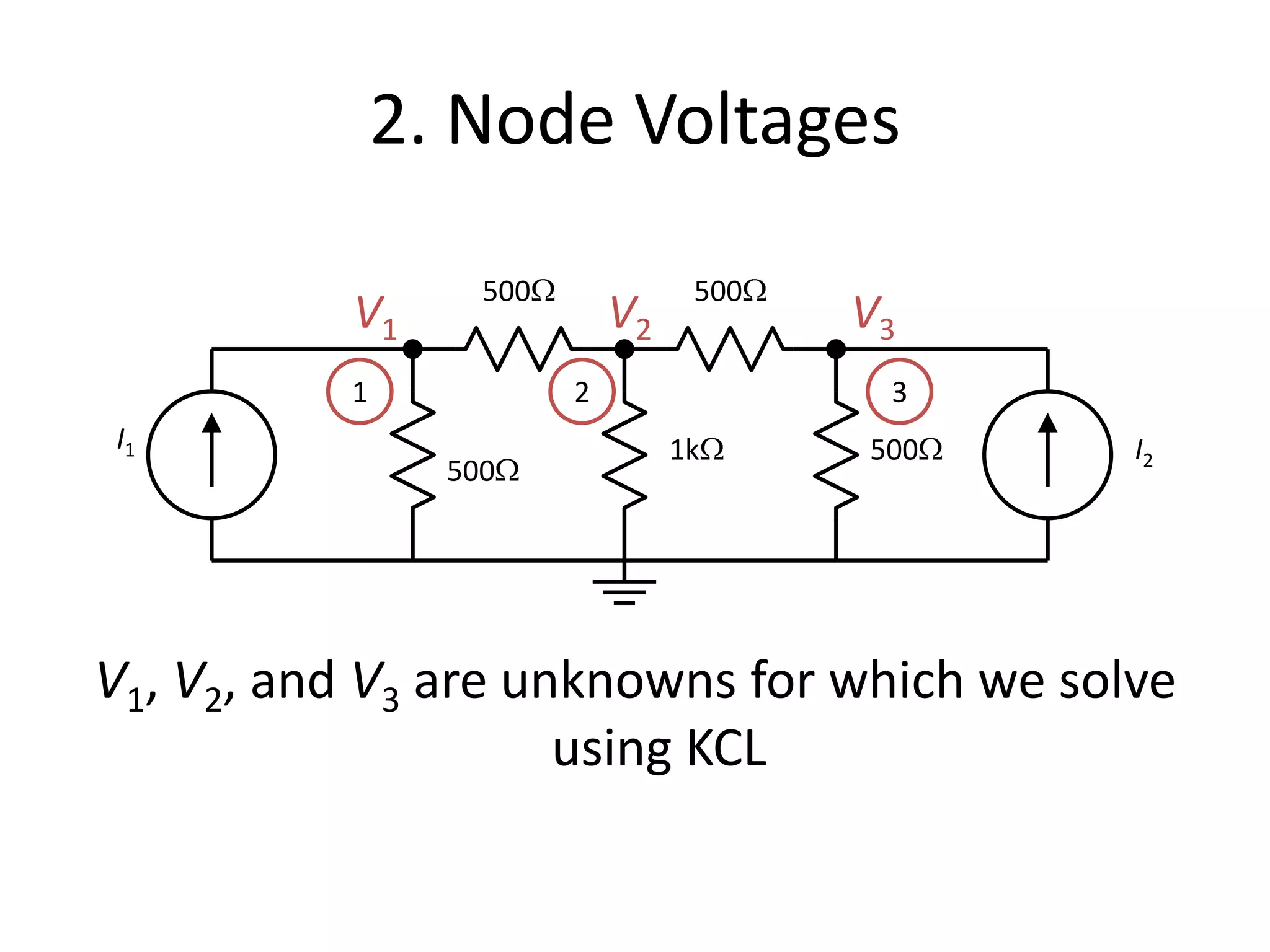
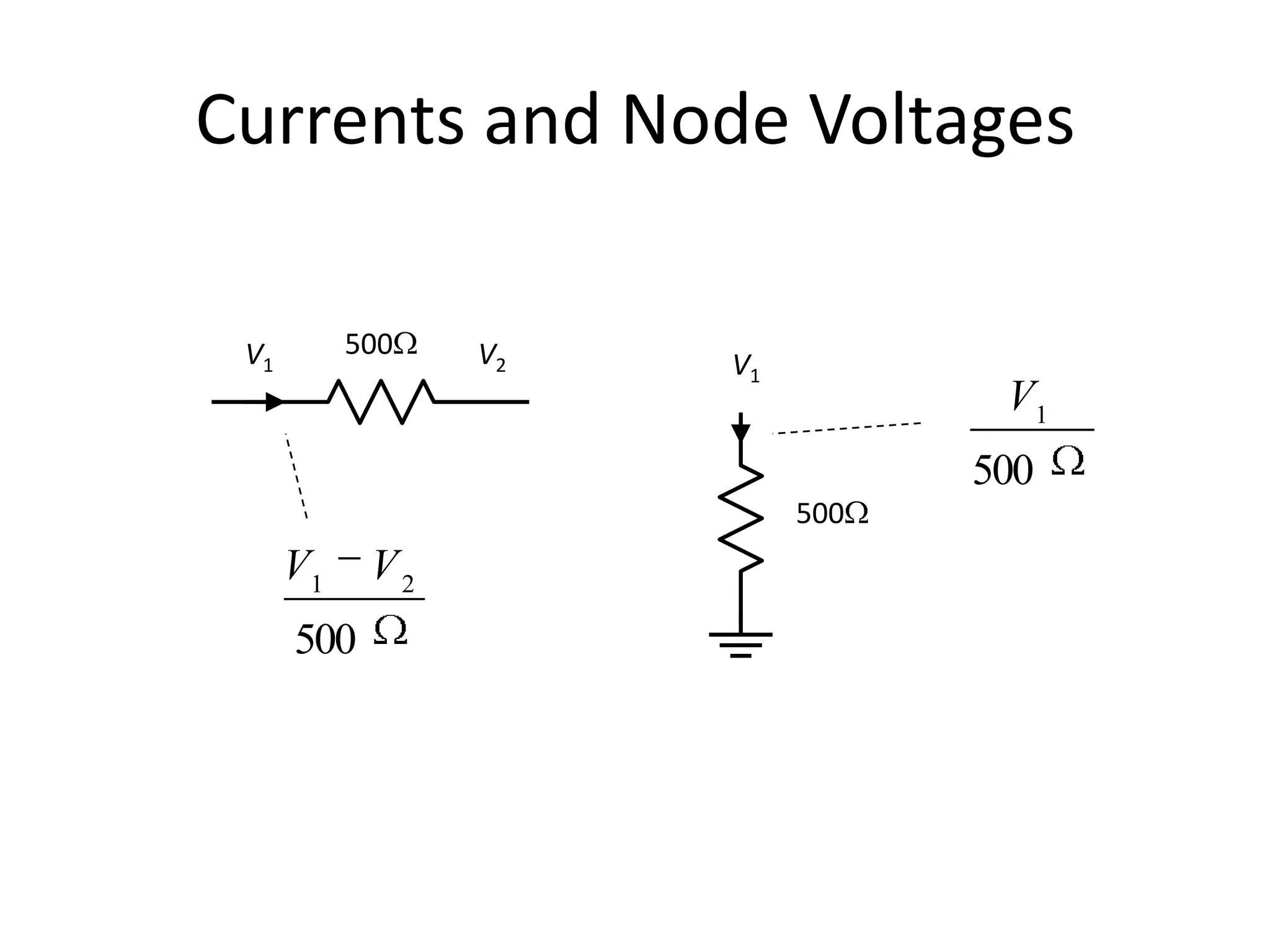
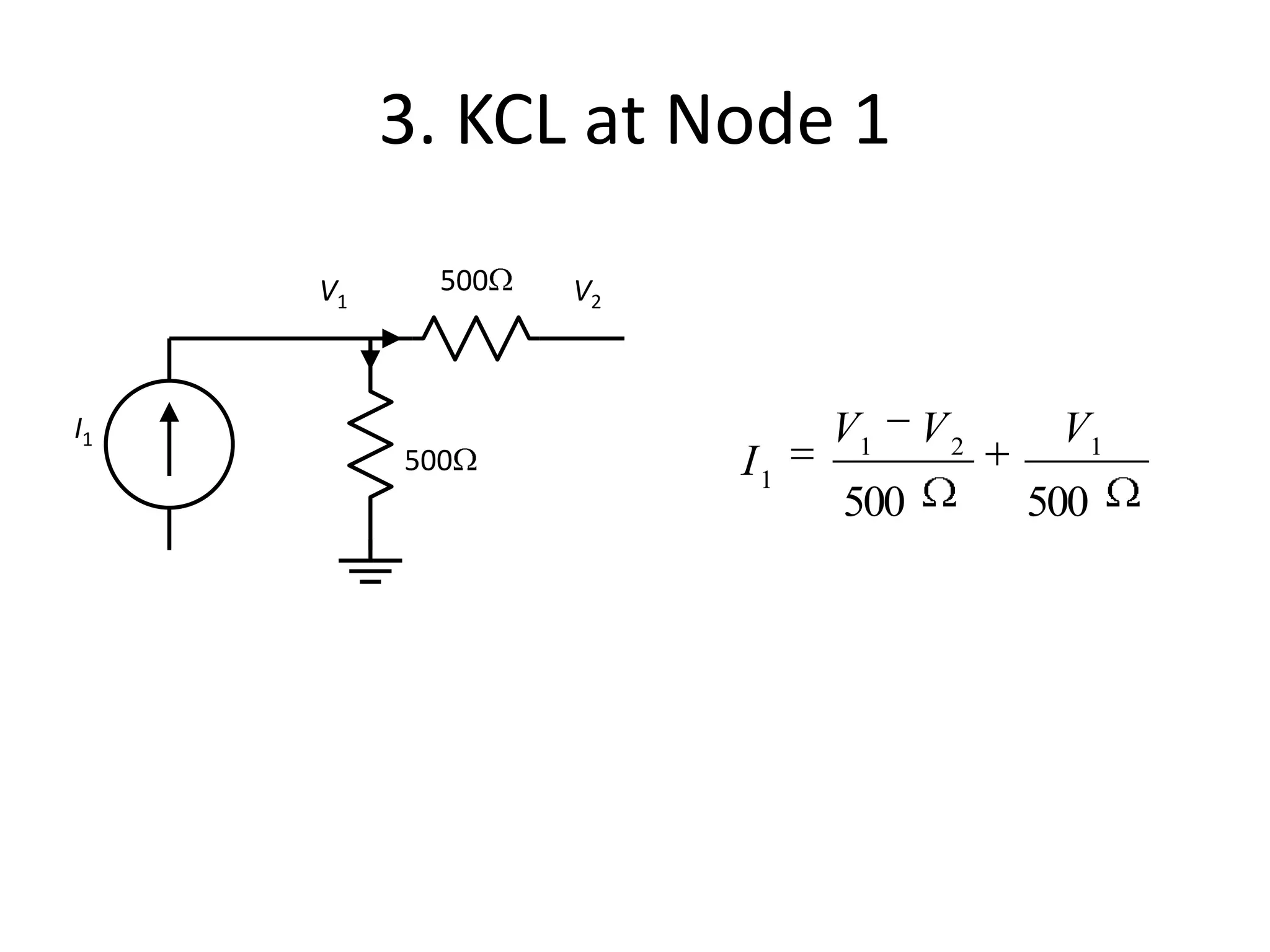
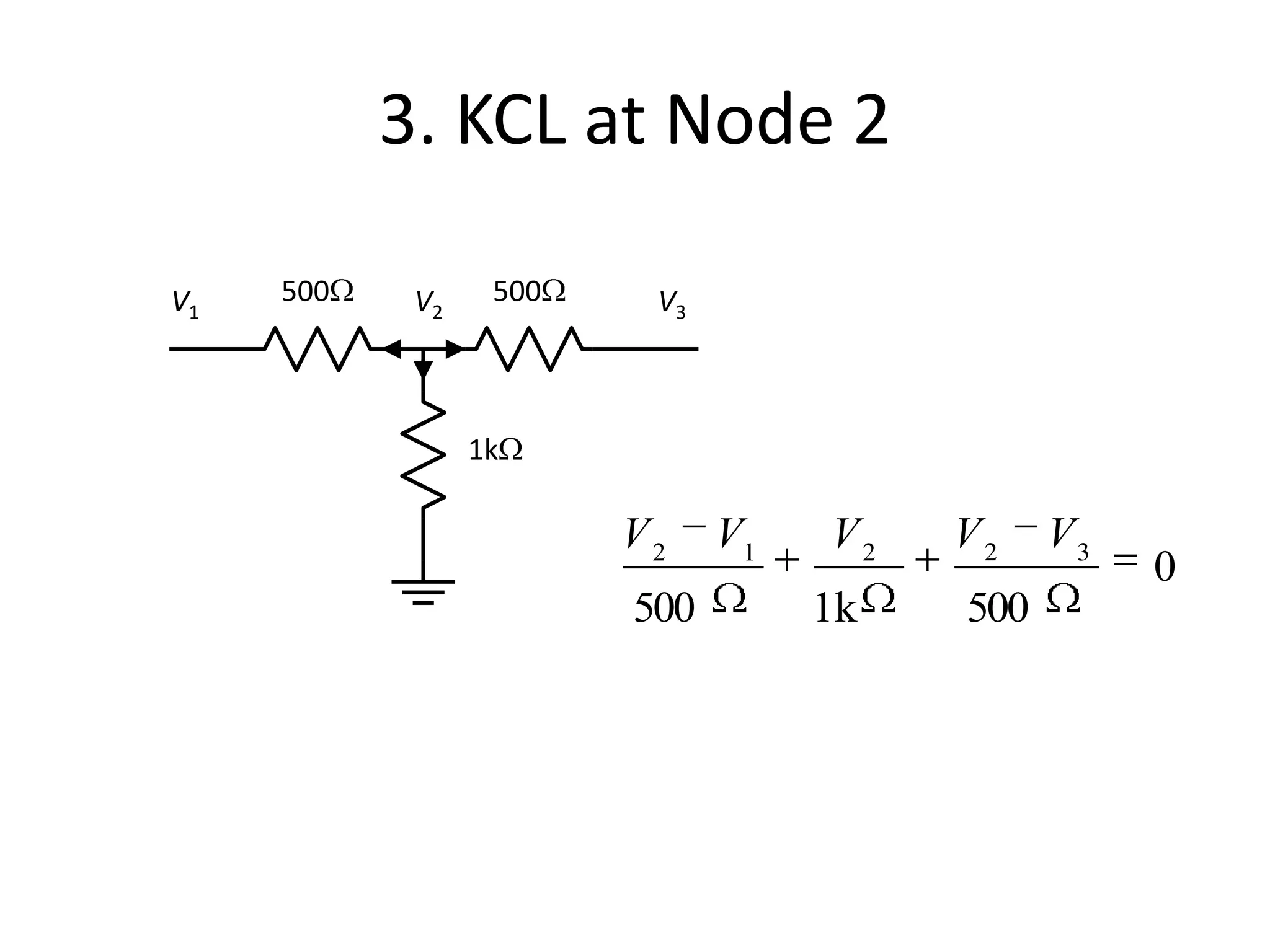
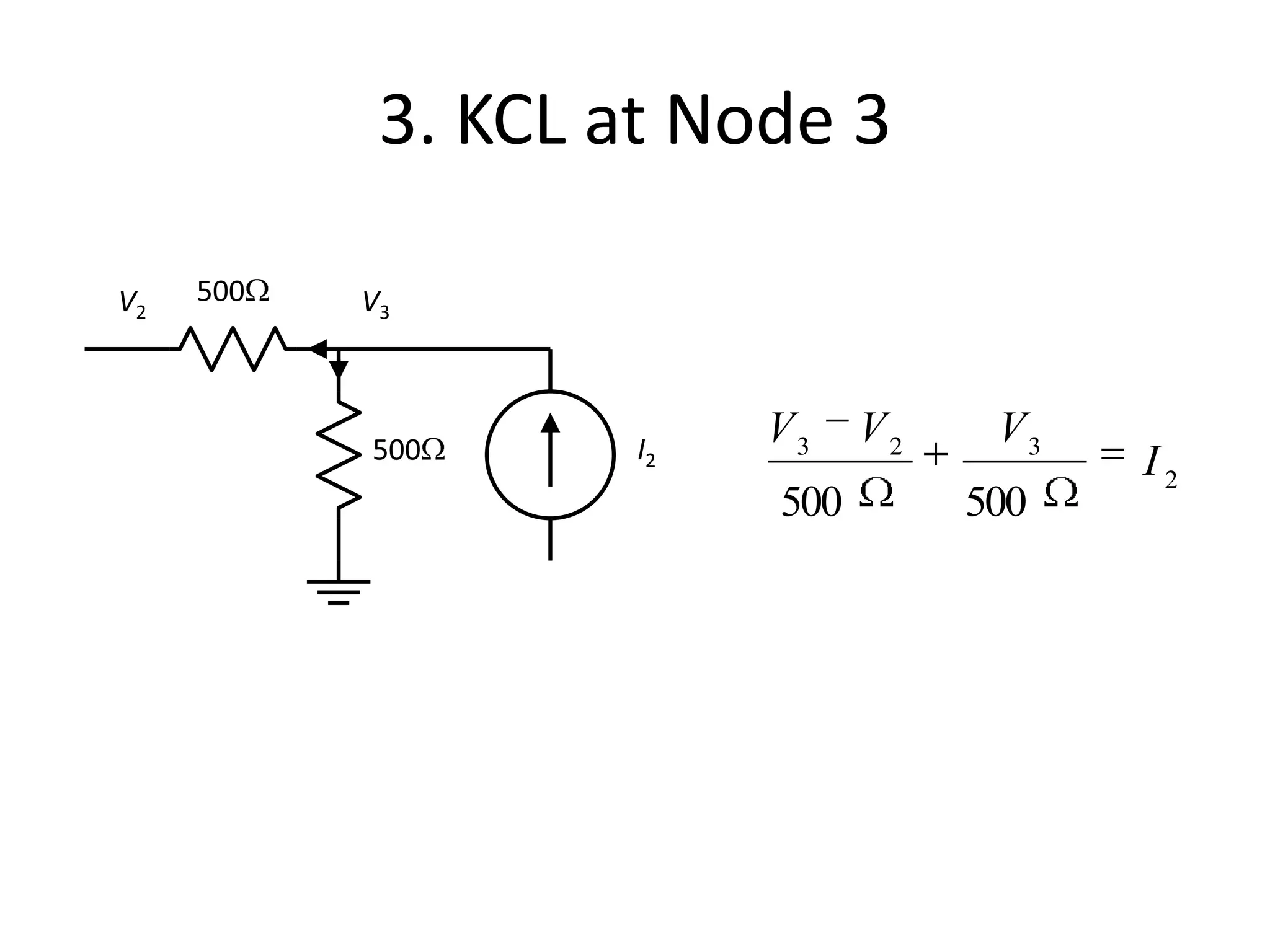
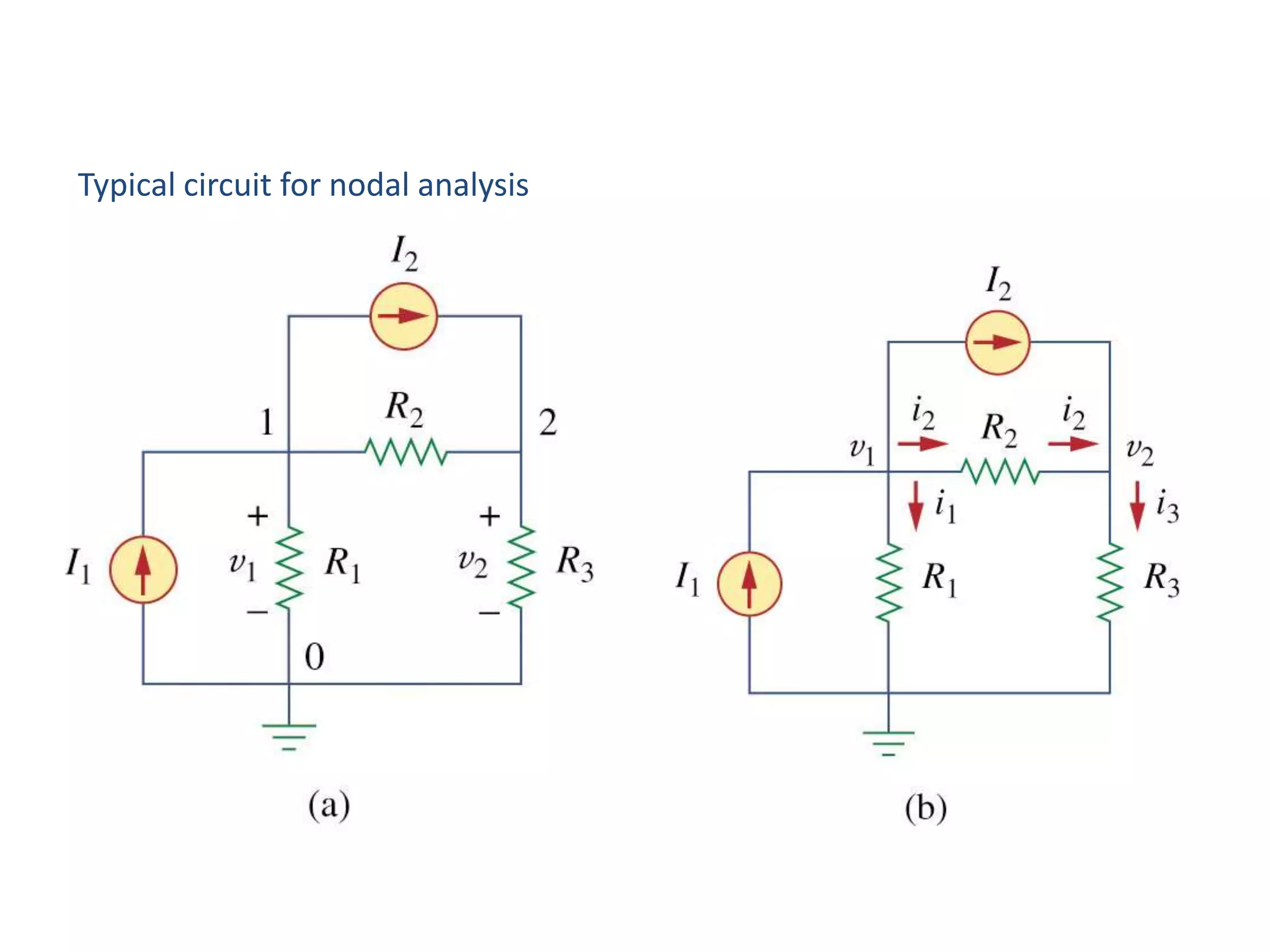
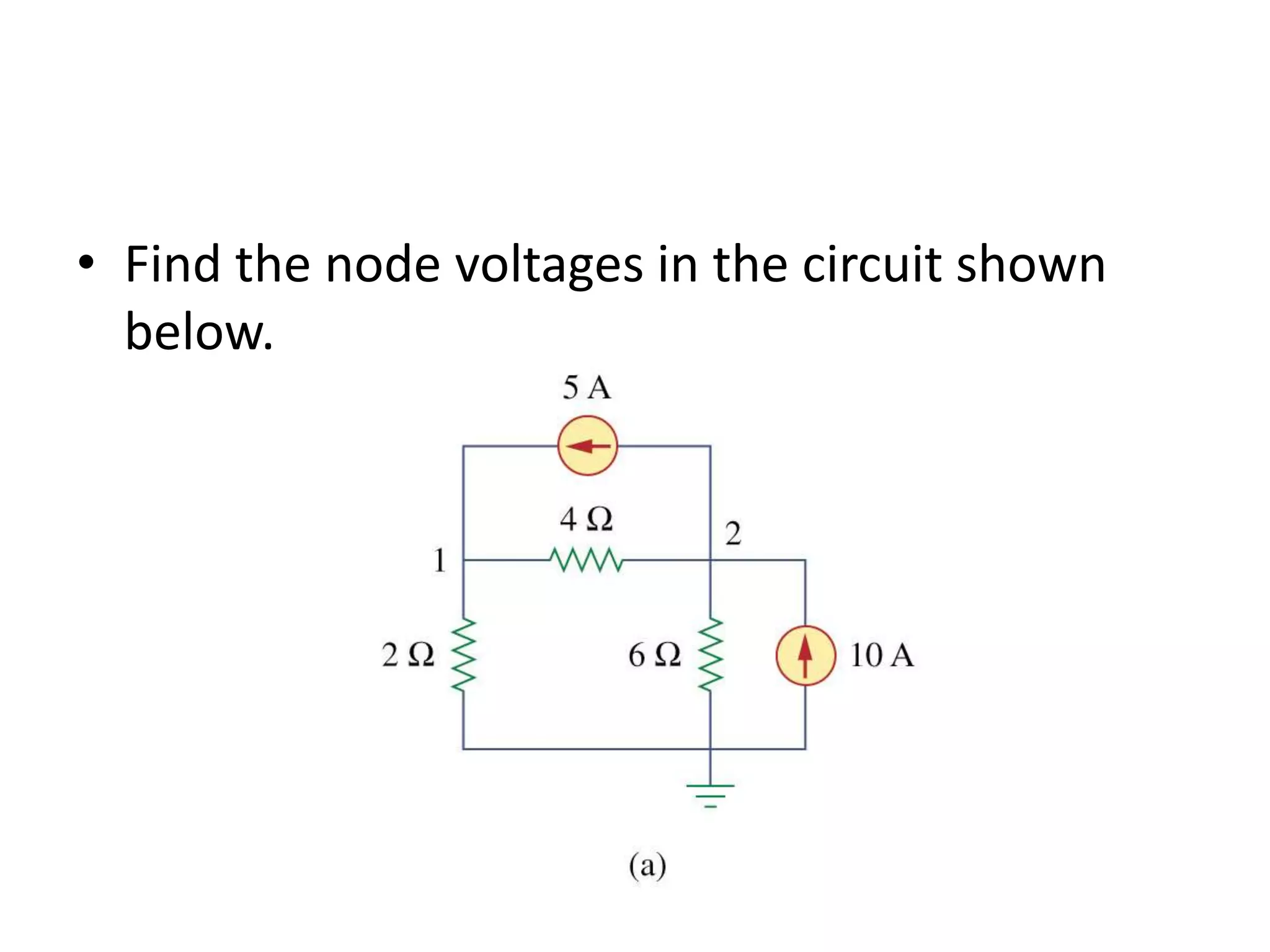
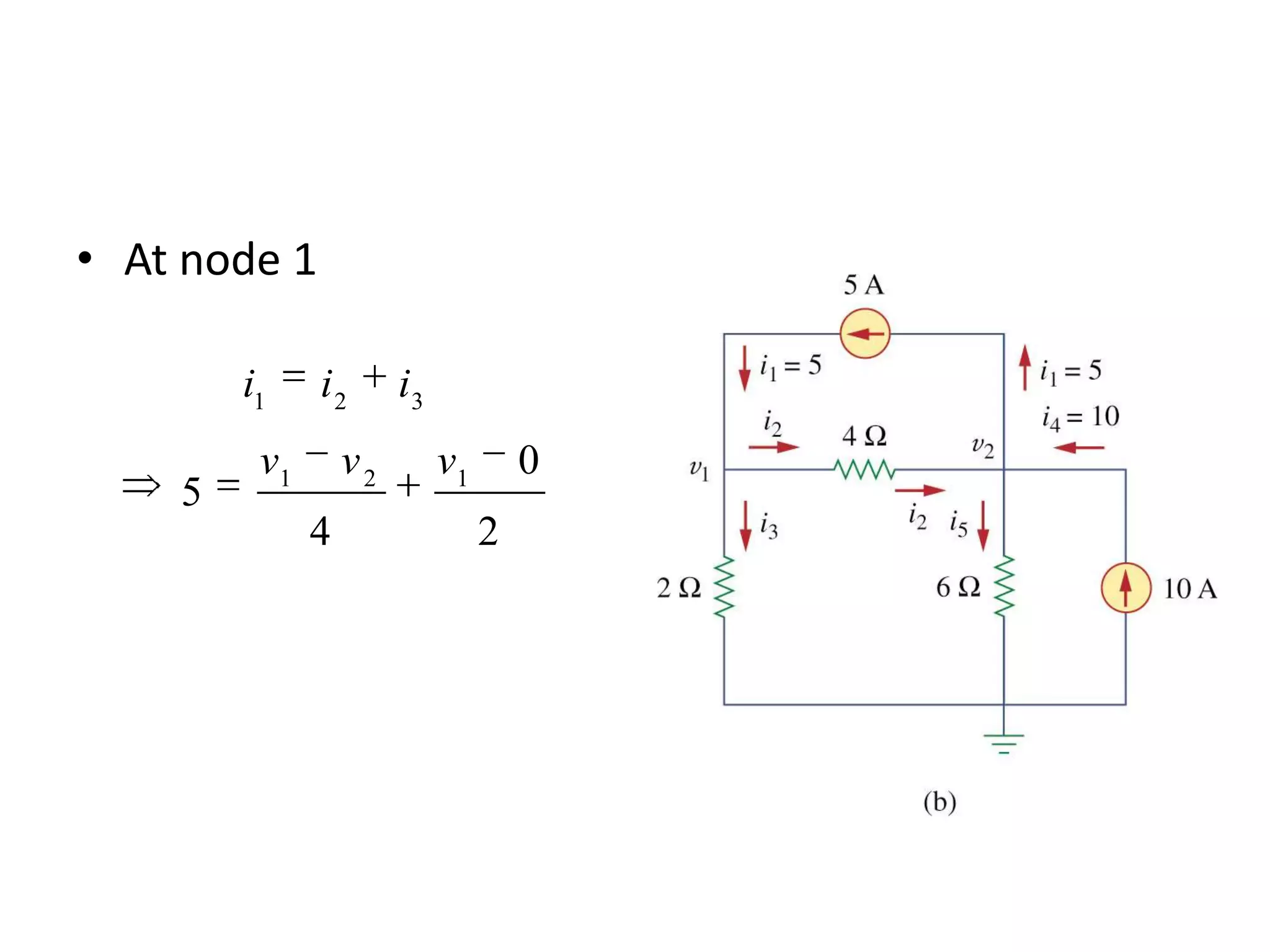
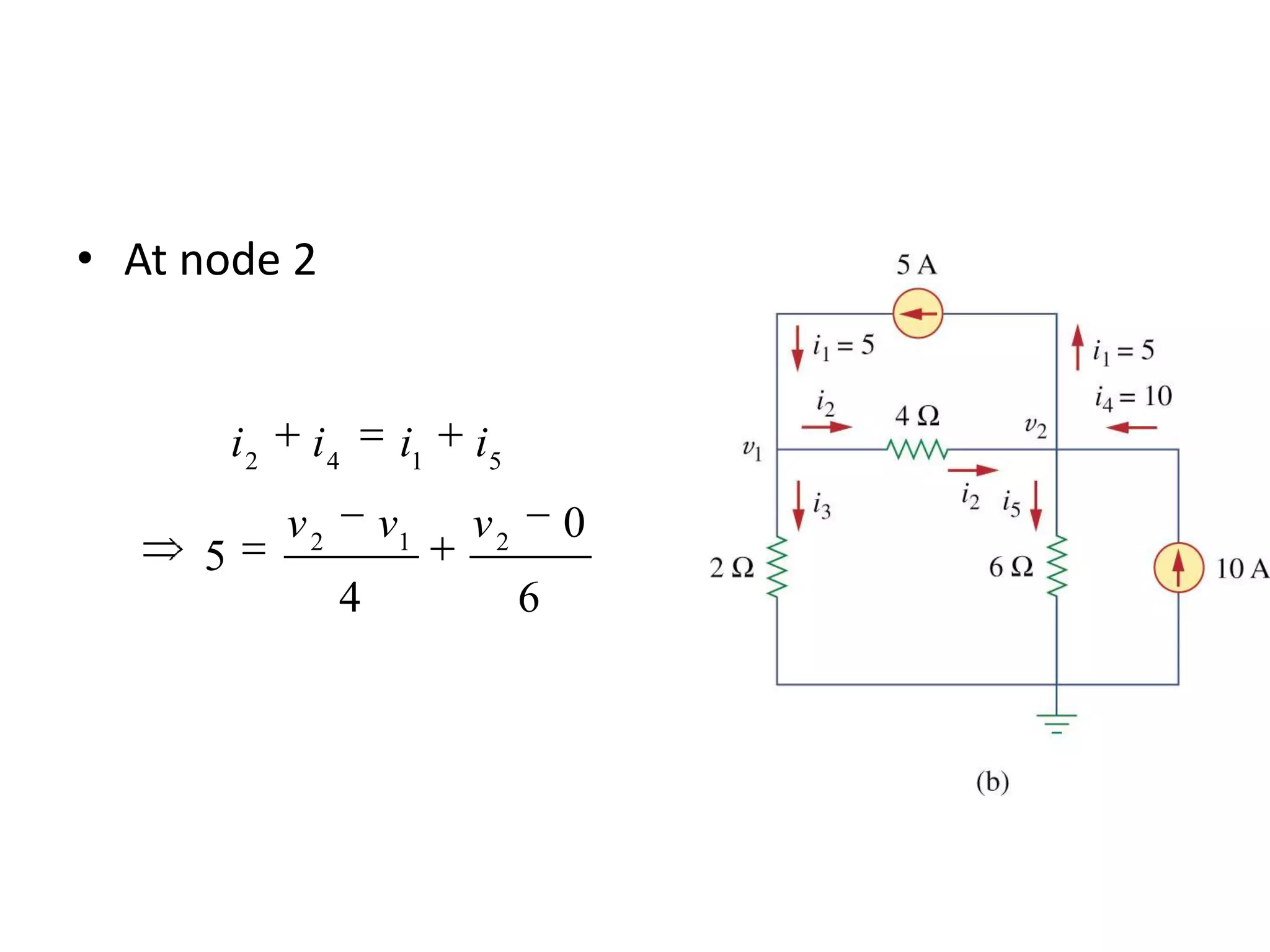
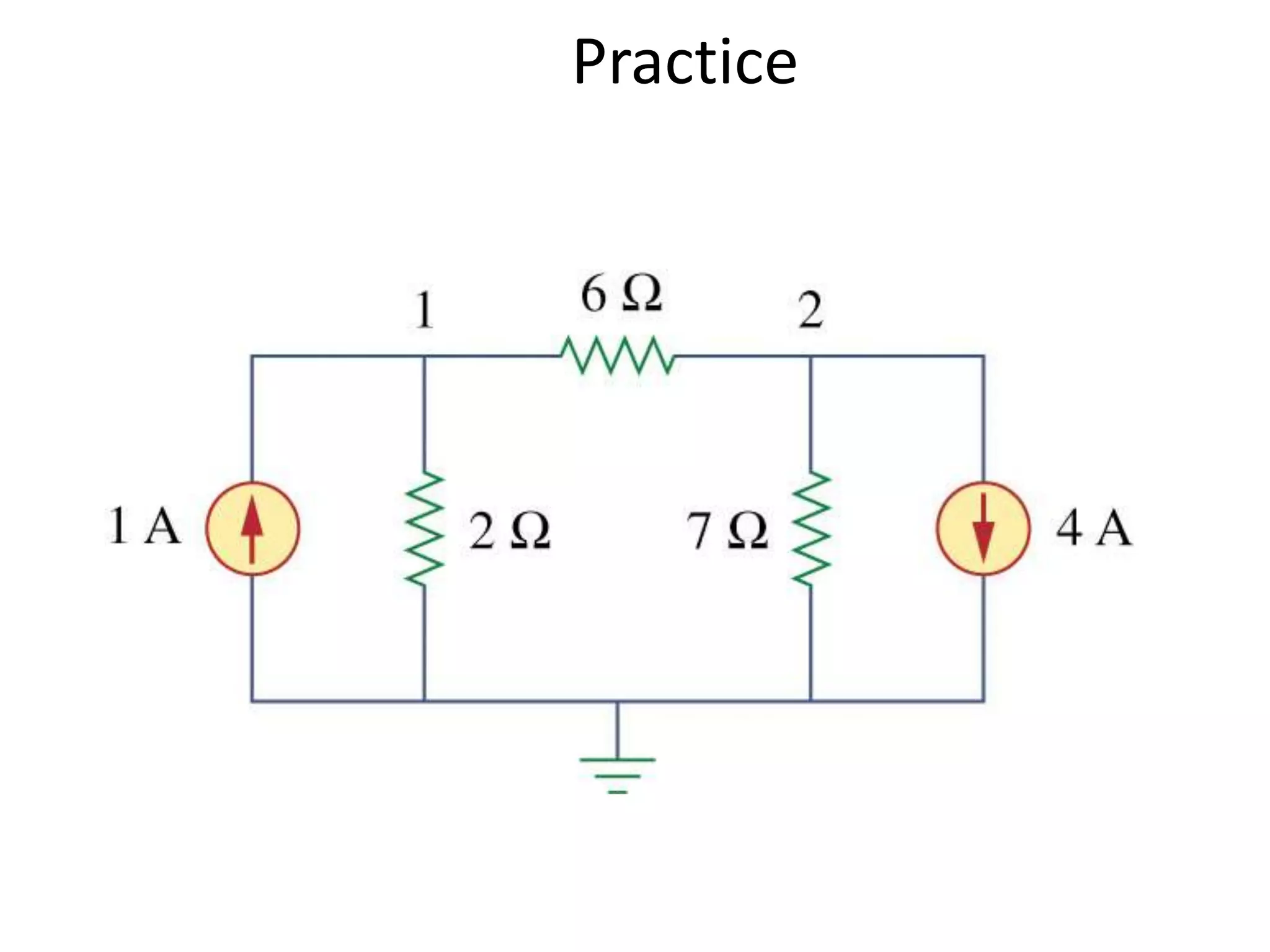
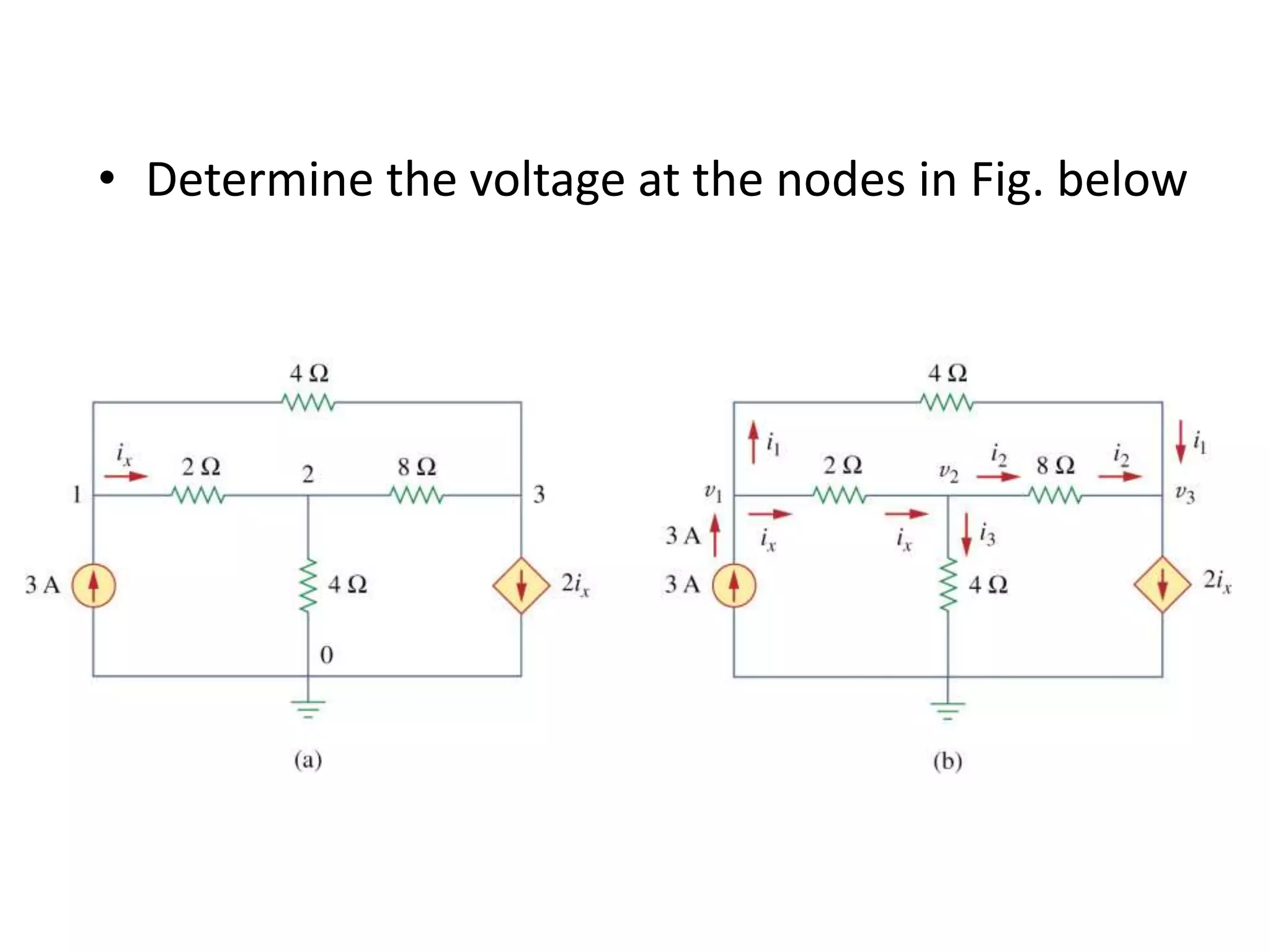
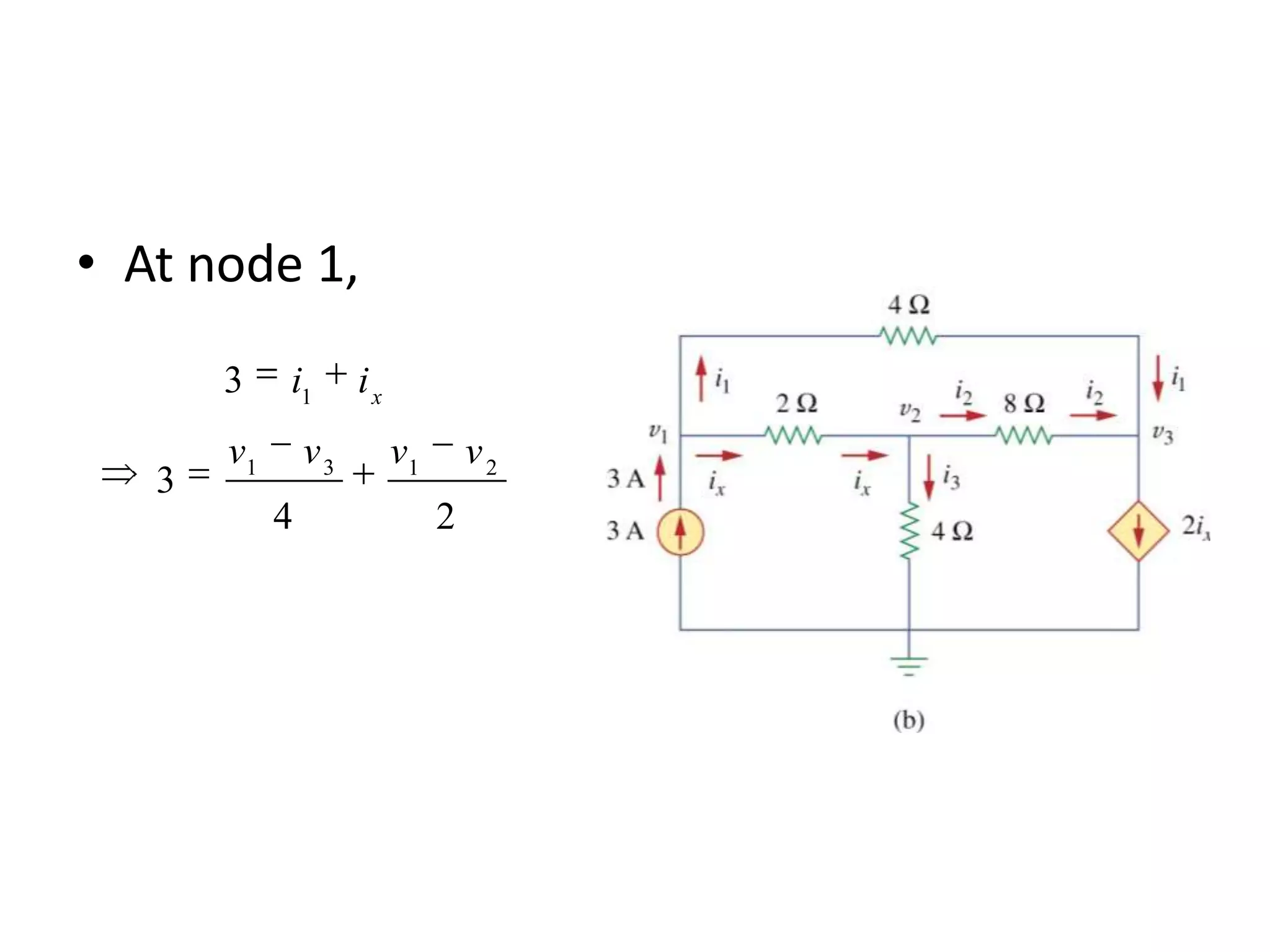
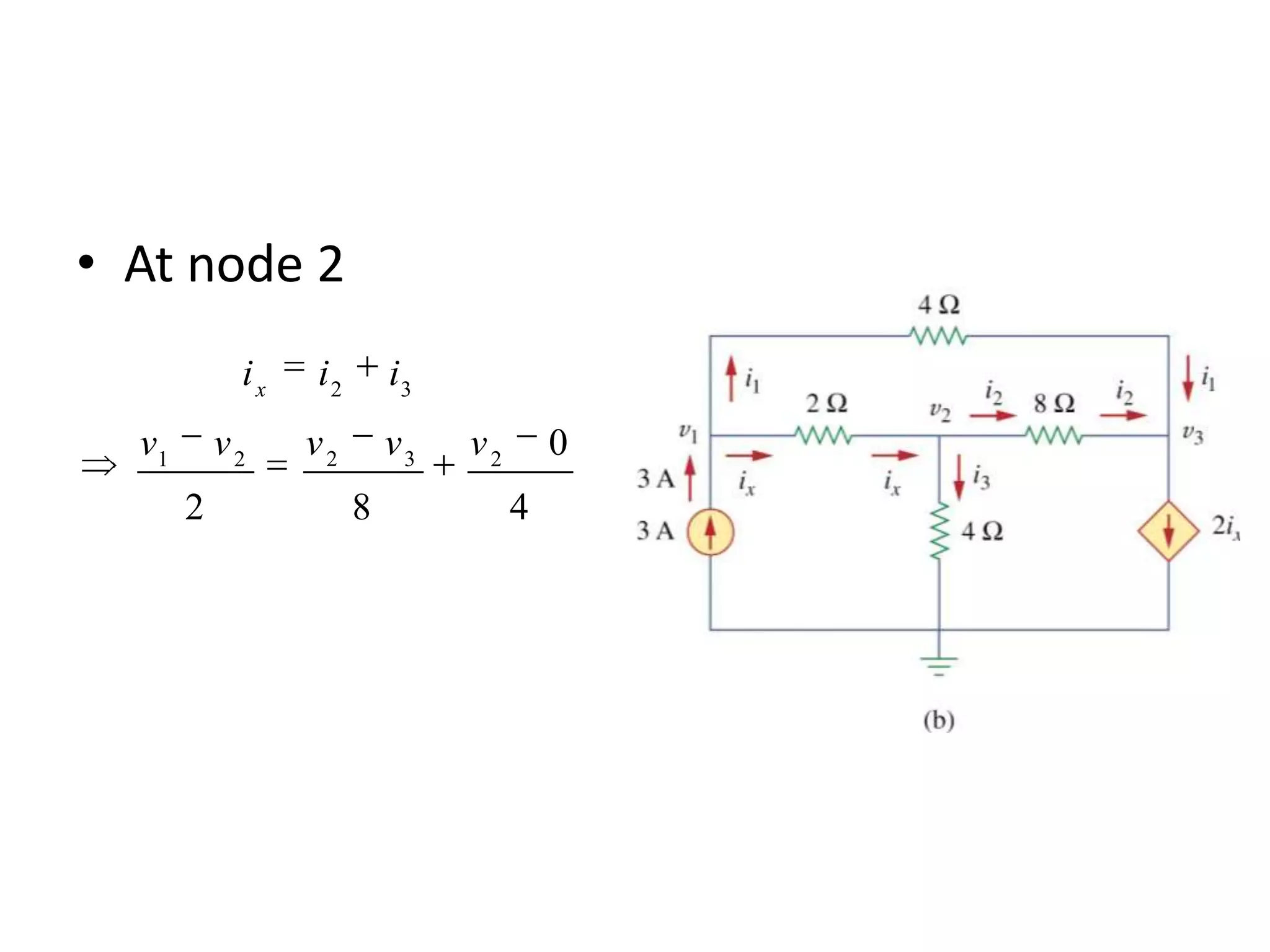
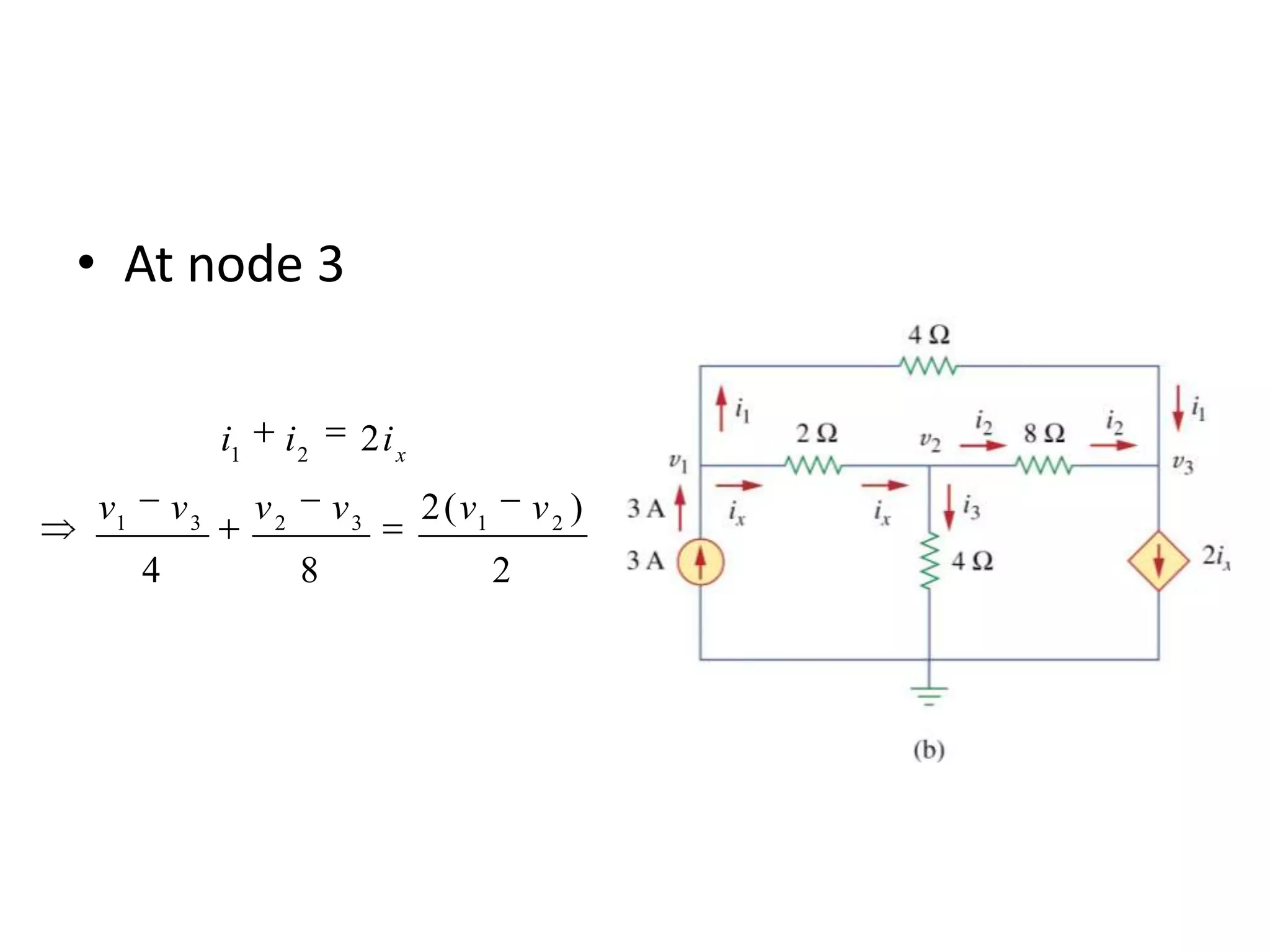
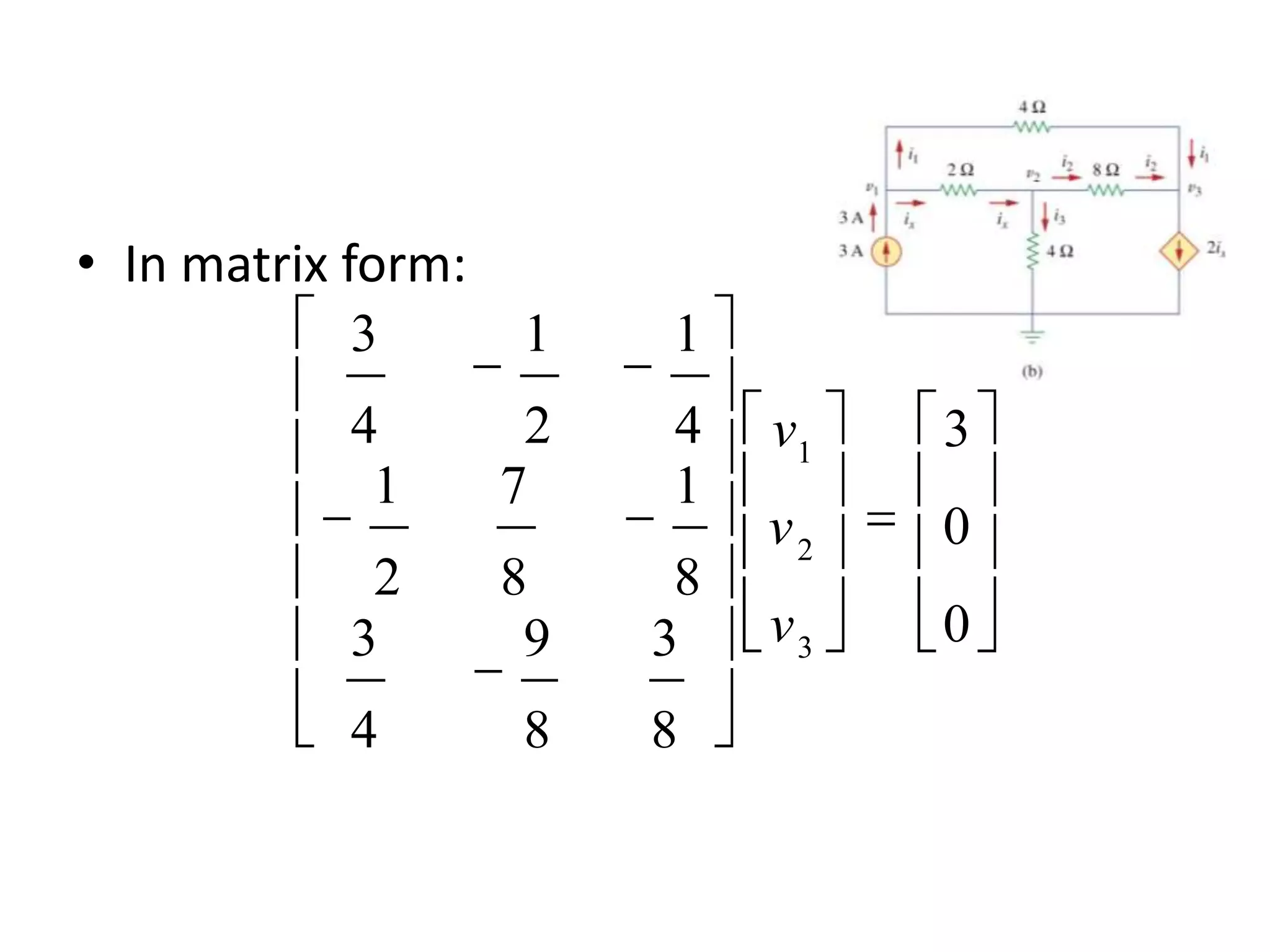
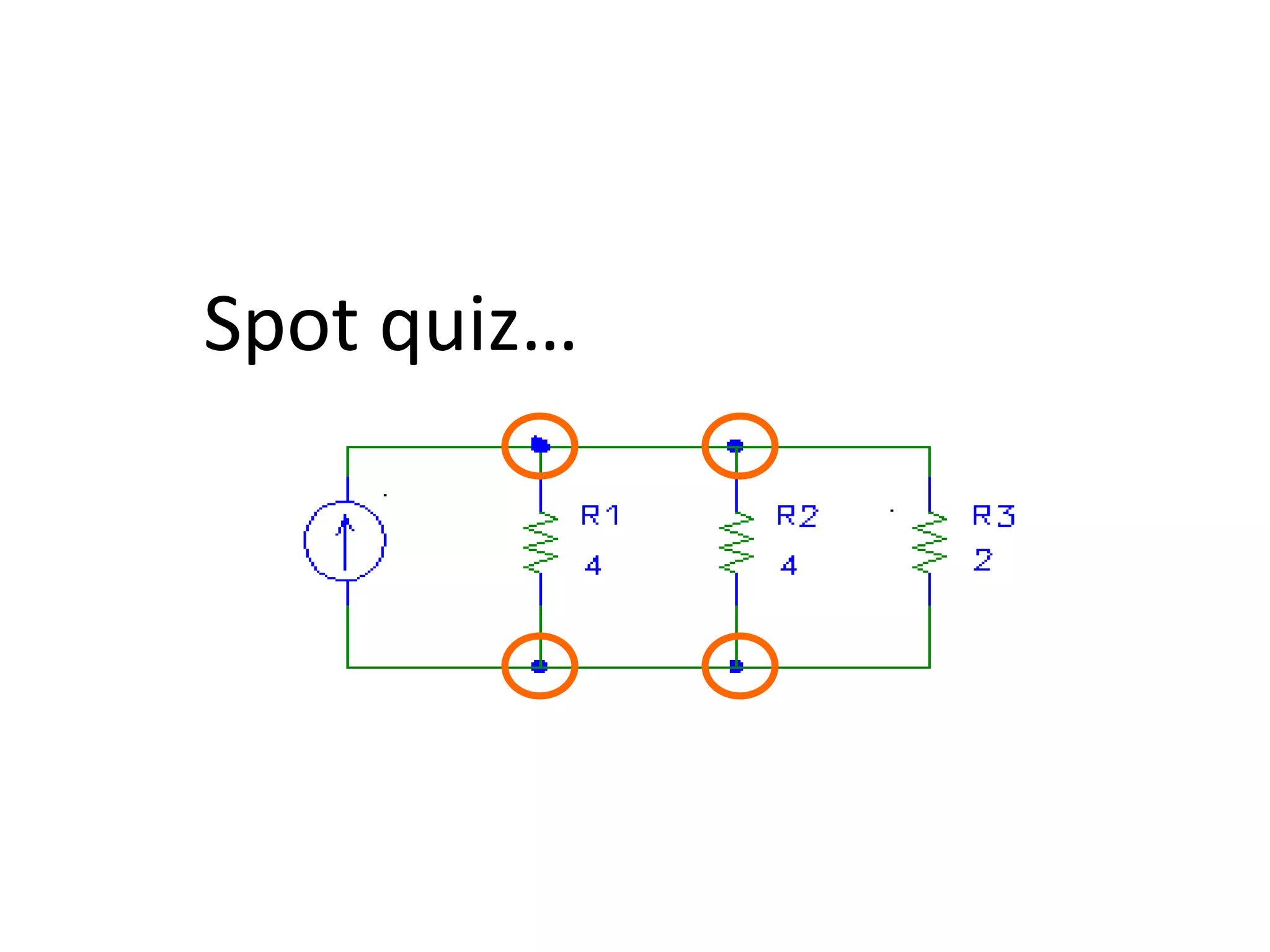
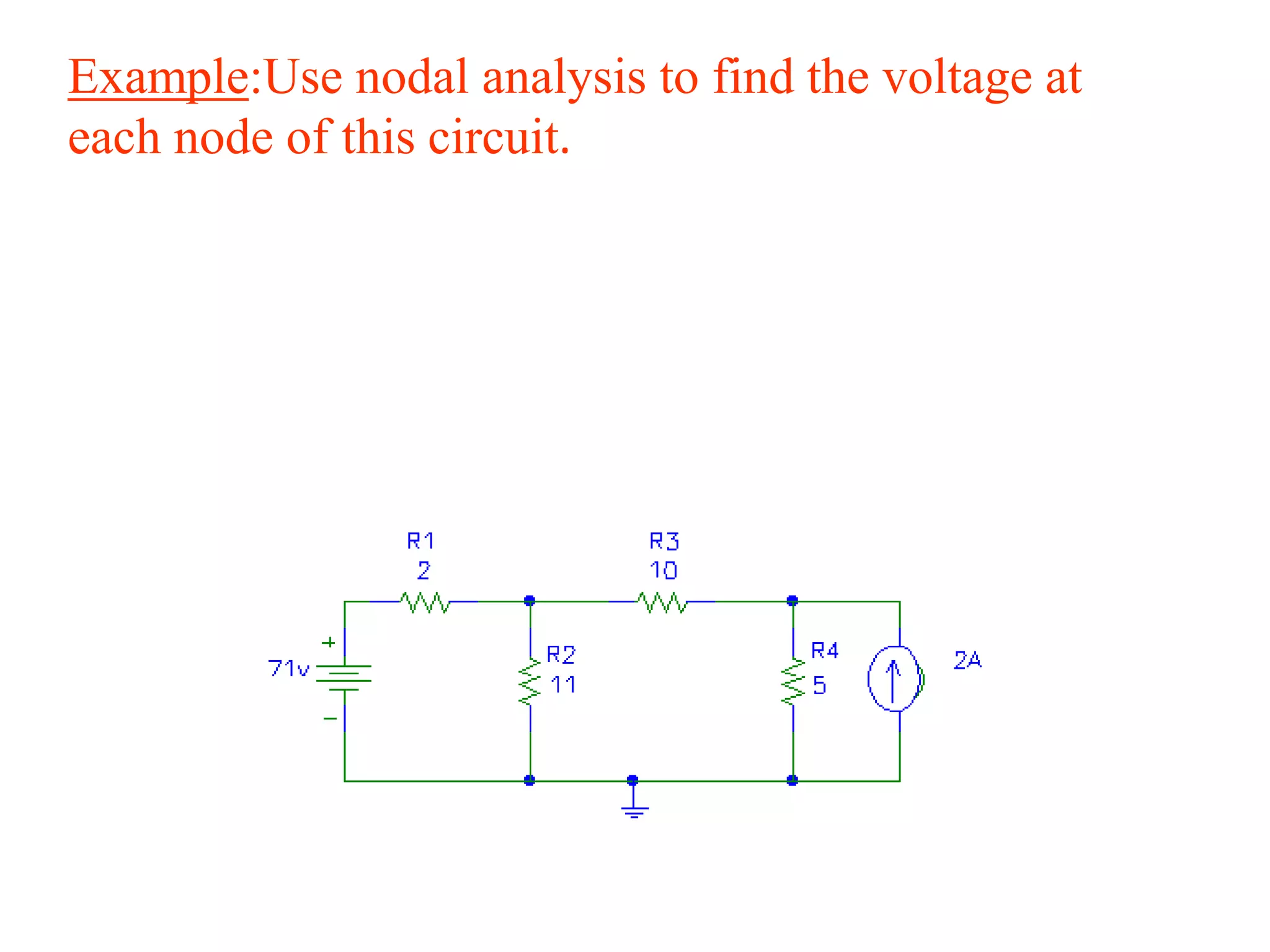
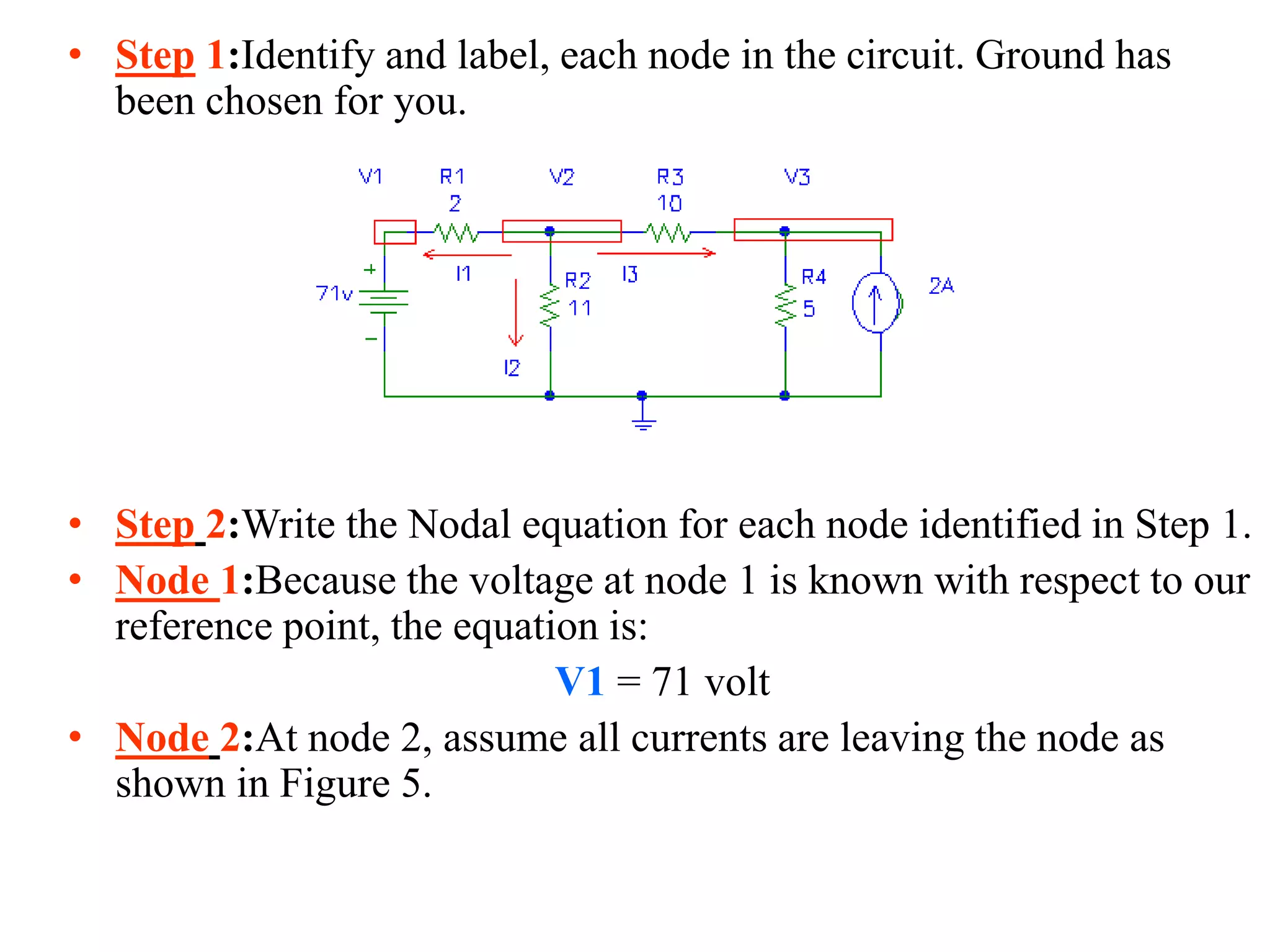
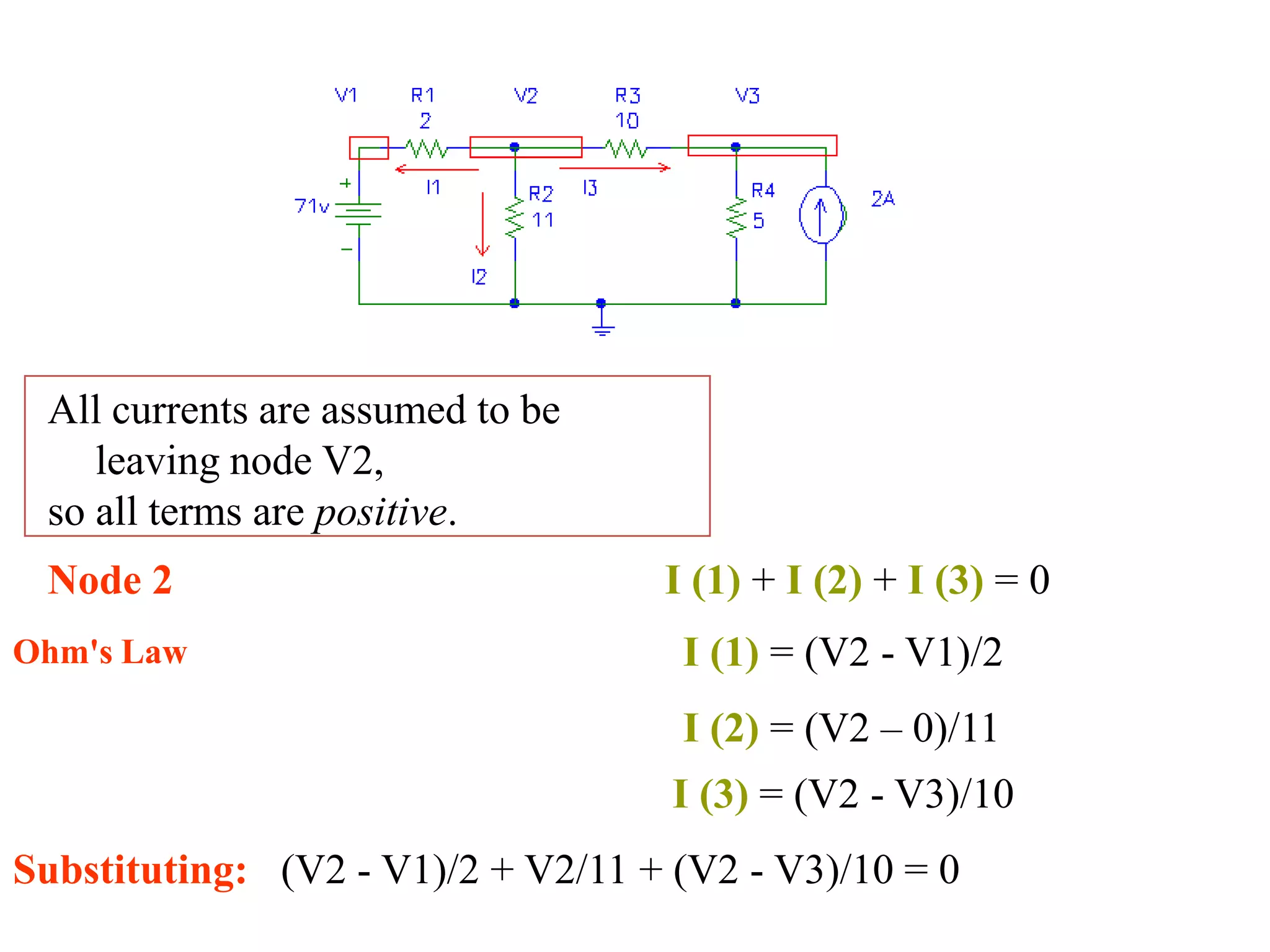
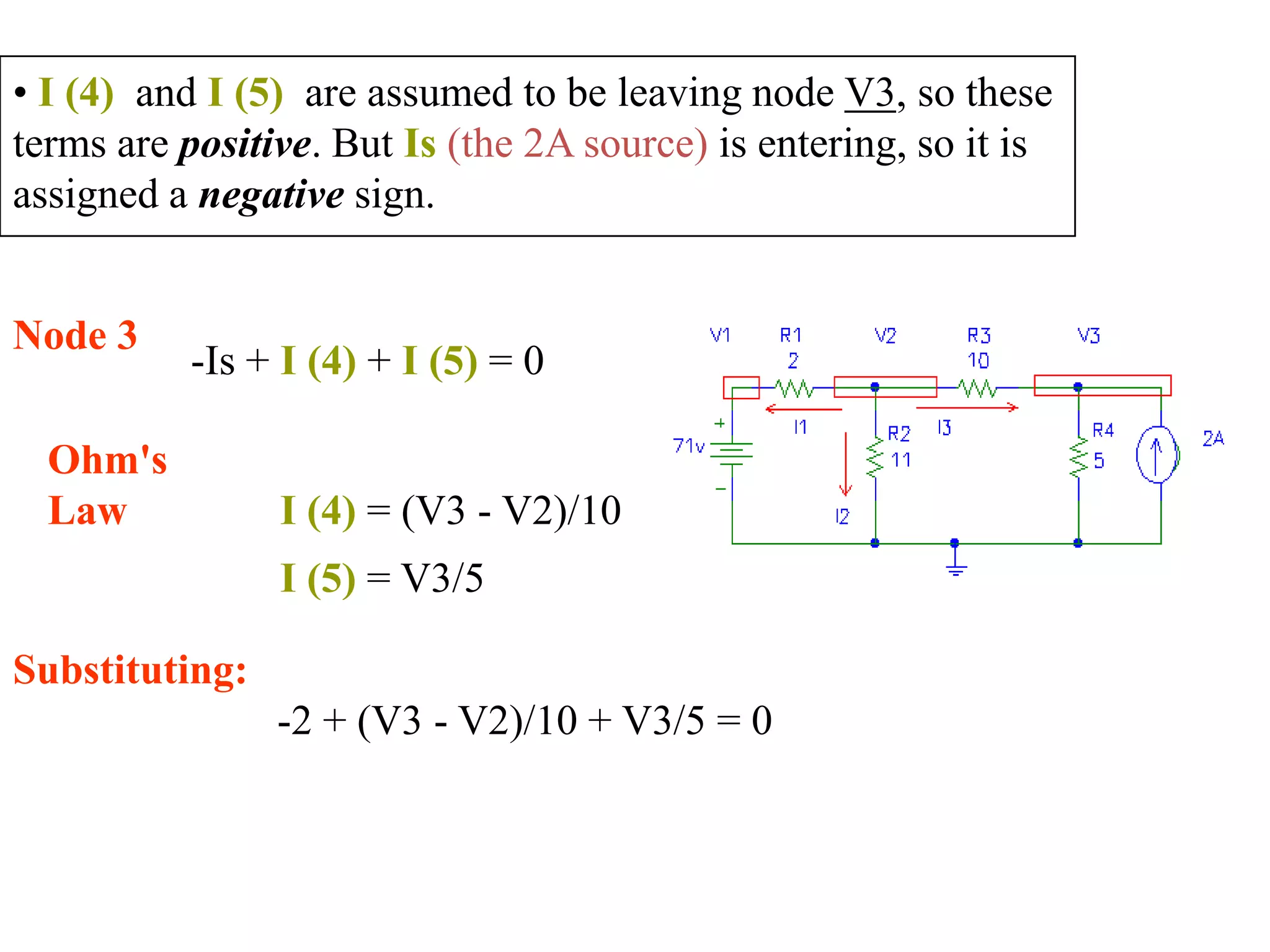
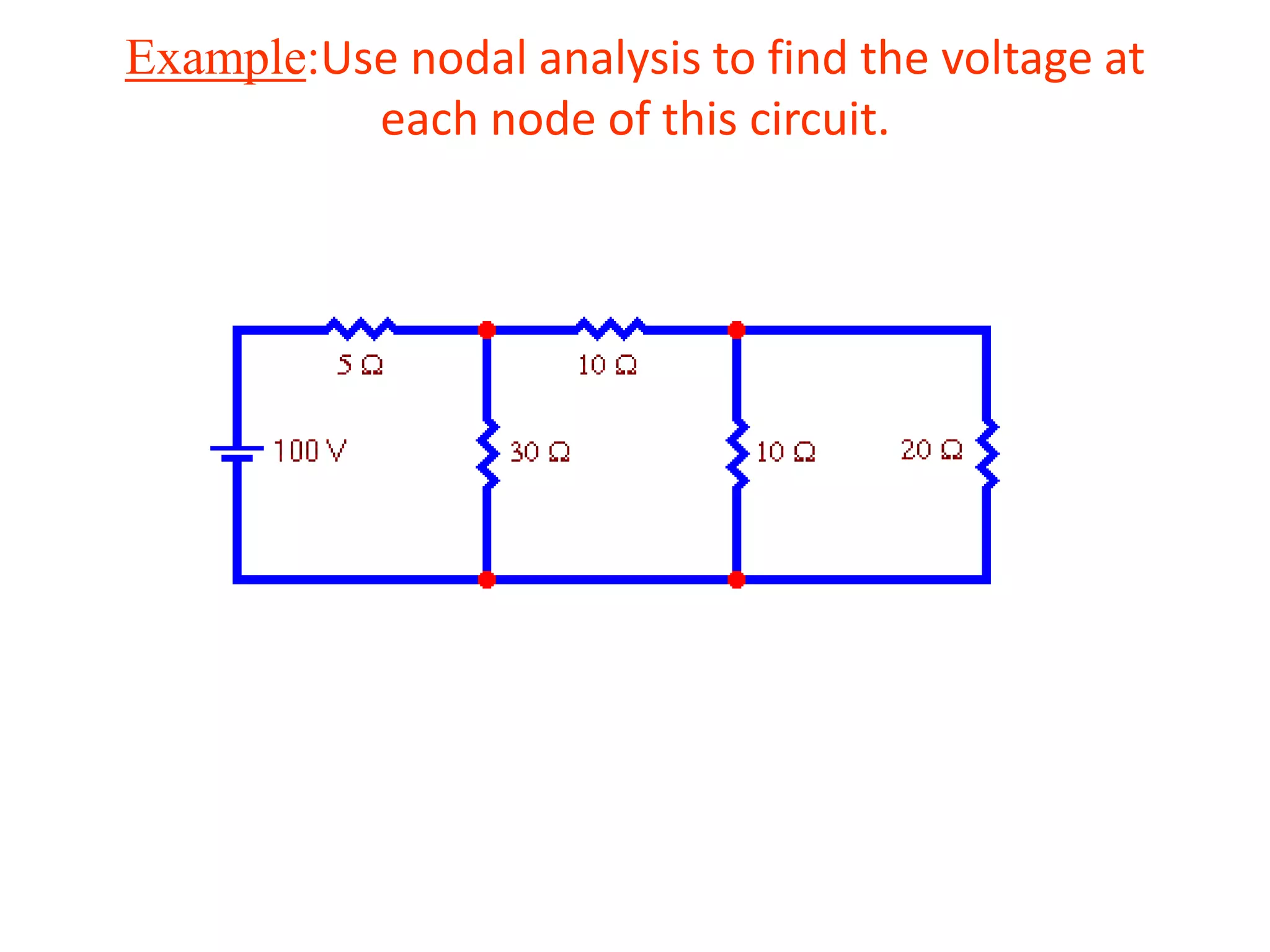
The document discusses nodal analysis for solving electric circuits. It explains the steps of nodal analysis which are: 1) choose a reference node, 2) assign voltages to each node, 3) apply Kirchhoff's Current Law at each node to write equations relating the currents and voltages, 4) solve the resulting system of equations. It provides an example circuit and writes out the nodal equations at each node to solve for the unknown node voltages.

1. Electric Circuit Analysis
Lec4: Nodal analysis
Ahsan Khawaja
Ahsan_khawaja@comsats.edu.pk
Lecturer
Room 102
Department of Electrical Engineering

2. Steps of Nodal Analysis
1. Choose a reference (ground) node.
2. Assign node voltages to the other nodes.
3. Apply KCL to each node other than the reference
node; express currents in terms of node voltages.
4. Solve the resulting system of linear equations for
the nodal voltages.

3. Common symbols for indicating a reference node,
(a) common ground, (b) ground, (c) chassis.

4. 1. Reference Node
The reference node is called the ground node
where V = 0
+
–
V 500
500
1k
500
500
I1 I2

5. Steps of Nodal Analysis
1. Choose a reference (ground) node.
2. Assign node voltages to the other nodes.
3. Apply KCL to each node other than the reference
node; express currents in terms of node voltages.
4. Solve the resulting system of linear equations for
the nodal voltages.

6. 2. Node Voltages
V1, V2, and V3 are unknowns for which we solve
using KCL
500
500
1k
500
500
I1 I2
1 2 3
V1 V2 V3

7. Steps of Nodal Analysis
1. Choose a reference (ground) node.
2. Assign node voltages to the other nodes.
3. Apply KCL to each node other than the reference
node; express currents in terms of node voltages.
4. Solve the resulting system of linear equations for
the nodal voltages.

8. Currents and Node Voltages
500
V1
500V1 V2
500
21
VV
500
1
V

9. 3. KCL at Node 1
500
500
I1
V1 V2
500500
121
1
VVV
I

10. 3. KCL at Node 2
500
1k
500 V2 V3V1
0
500k1500
32212
VVVVV

11. 3. KCL at Node 3
2
323
500500
I
VVV500
500
I2
V2 V3

12. Steps of Nodal Analysis
1. Choose a reference (ground) node.
2. Assign node voltages to the other nodes.
3. Apply KCL to each node other than the reference
node; express currents in terms of node voltages.
4. Solve the resulting system of linear equations for
the nodal voltages.

13. Typical circuit for nodal analysis

14. • Find the node voltages in the circuit shown
below.

15. • At node 1
2
0
4
5 121
321
vvv
iii

16. • At node 2
6
0
4
5 212
5142
vvv
iiii

17. Practice

18. • Determine the voltage at the nodes in Fig. below

19. • At node 1,
24
3
3
2131
1
vvvv
ii x

20. • At node 2
4
0
82
23221
32
vvvvv
iiix

21. • At node 3
2
)(2
84
2
213231
21
vvvvvv
iii x

22. • In matrix form:
0
0
3
8
3
8
9
4
3
8
1
8
7
2
1
4
1
2
1
4
3
3
2
1
v
v
v

23. Spot quiz…

24. Example:Use nodal analysis to find the voltage at
each node of this circuit.

25. • Step 1:Identify and label, each node in the circuit. Ground has
been chosen for you.
• Step 2:Write the Nodal equation for each node identified in Step 1.
• Node 1:Because the voltage at node 1 is known with respect to our
reference point, the equation is:
V1 = 71 volt
• Node 2:At node 2, assume all currents are leaving the node as
shown in Figure 5.

26. All currents are assumed to be
leaving node V2,
so all terms are positive.
Node 2 I (1) + I (2) + I (3) = 0
Ohm's Law I (1) = (V2 - V1)/2
I (2) = (V2 – 0)/11
I (3) = (V2 - V3)/10
Substituting: (V2 - V1)/2 + V2/11 + (V2 - V3)/10 = 0

27. • I (4) and I (5) are assumed to be leaving node V3, so these
terms are positive. But Is (the 2A source) is entering, so it is
assigned a negative sign.
Node 3
-Is + I (4) + I (5) = 0
Ohm's
Law I (4) = (V3 - V2)/10
I (5) = V3/5
Substituting:
-2 + (V3 - V2)/10 + V3/5 = 0

28. • The three equations are shown below:
Node 1: V1 = 71v
Node 2 : (V2 - V1)/2 + V2/11 + (V2 - V3)/10 = 0
Node 3: -2 + (V3 - V2)/10 + V3/5 = 0
• After solving we find that the node voltages are:
V1 = 71v
V2 = 55v
V3 = 25v

29. Example:Use nodal analysis to find the voltage at
each node of this circuit.