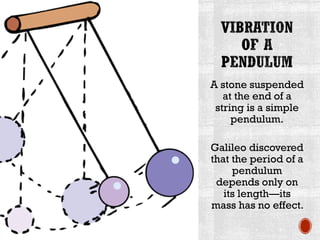
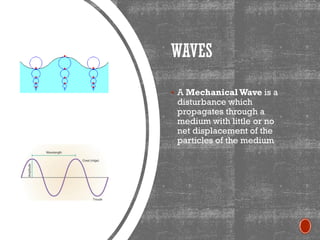
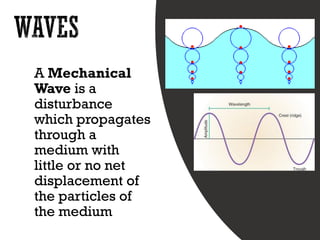
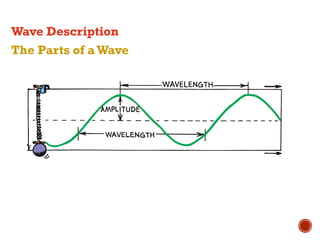
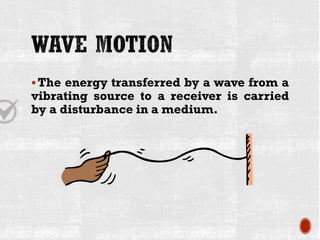
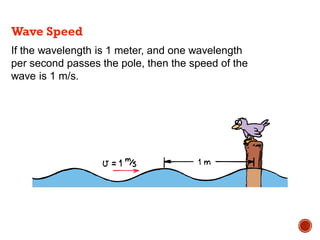
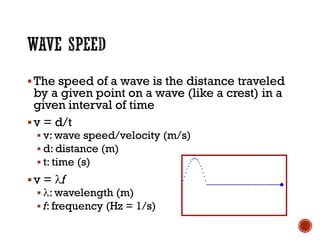
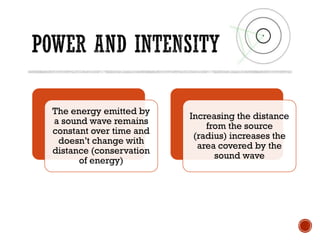
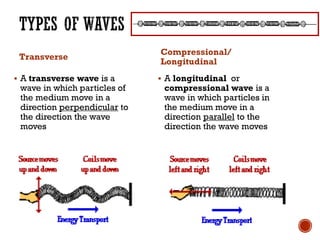
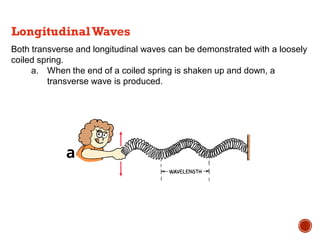
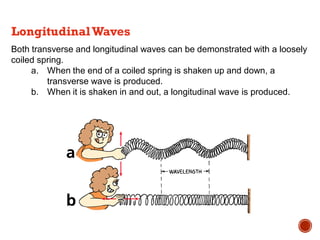
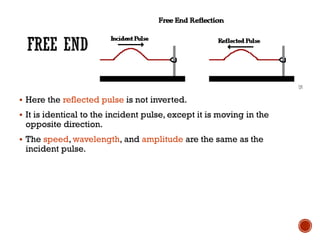
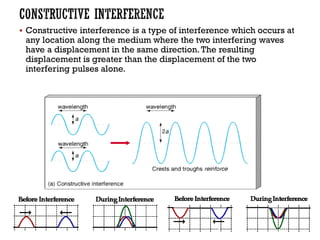
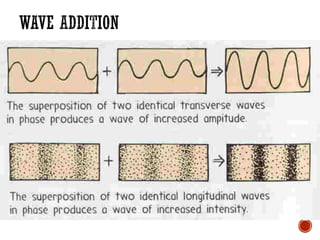
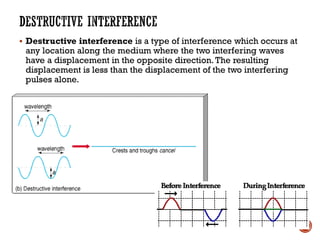
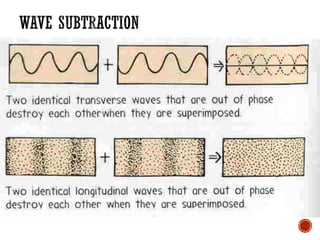
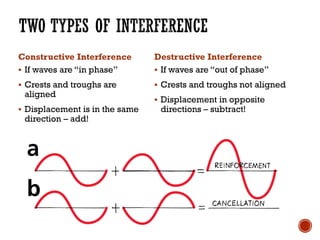
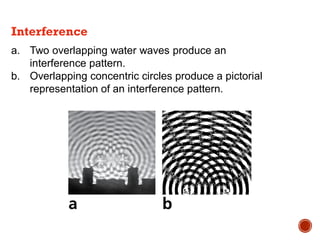
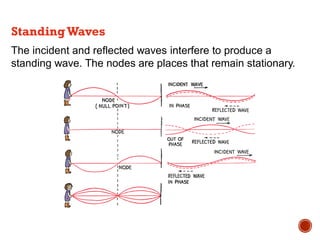
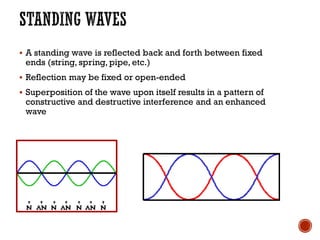
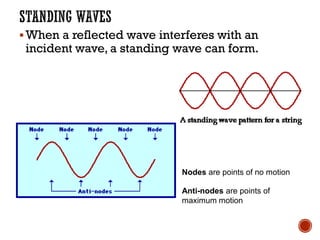
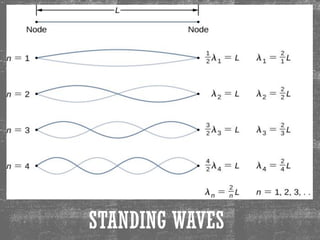
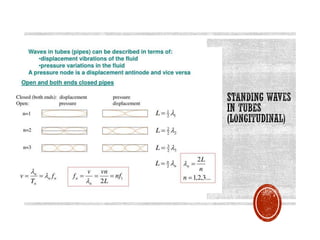
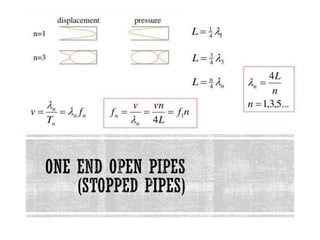
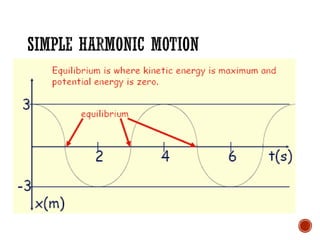
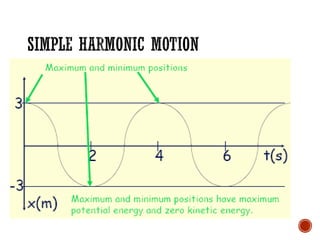
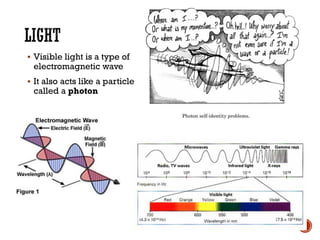
This document provides information about waves and wave phenomena. It discusses the key characteristics of waves like frequency, wavelength, amplitude, and speed. It explains different types of waves including transverse, longitudinal, and standing waves. The document also covers wave behavior at boundaries, interference, reflection, the Doppler effect, and more. Concepts are defined and illustrated with diagrams. The document is intended as a comprehensive reference on the physics of waves and wave motion.