Water undergoes self-ionization in which a small percentage of water molecules dissociate into hydronium (H3O+) and hydroxide (OH-) ions. The concentration of these ions is extremely small and the equilibrium lies very much in the forward direction. The self-ionization of water can be represented by the equilibrium constant Kw, which is equal to the product of the hydronium and hydroxide ion concentrations. Kw is temperature dependent and decreases with increasing temperature. The pH scale was developed to quantify the concentration of hydronium ions in solution and thus indicate whether a solution is acidic, basic, or neutral. pH is defined as the negative logarithm of the hydronium ion concentration

1. Water undergoes Self Ionisation
⇄
H2O(l)
H+(aq)
+
OH-(aq)
or
H2O(l)
+
H2O(l) ⇄
H3O
+
(aq)
+
-
OH (aq)
The concentration of H+ ions and OH- ions
is extremely small.
Because the equilibrium lies very much on the left hand

2. H2O(l)
⇄
H+(aq) +
Kc
OH-(aq)
=
In the above expression, the value of [H2O] may be taken as having a
constant value because the degree of ionisation is so small.
Kc
=
Kc [H2O] = [H+] [OH-]
Both Kc and [H2O] are constant values so
Kw = Kc [H2O] = [H+] [OH-]

3. T (°C)
Kw (mol2/litre2)
0
0.114 x 10-14
10
0.293 x 10-14
20
0.681 x 10-14
25
1.008 x 10-14
30
1.471 x 10-14
40
2.916 x 10-14
50
5.476 x 10-14
Kw of pure water decreases as the temperature increases

4. Acid–Base Concentrations in Solutions

5. Acid–Base Concentrations in Solutions
concentration (moles/L)
10-1
OH-
H+
10-7
H+
OH-
OH-
H+
10-14
[H+] > [OH-]
[H+] = [OH-]
acidic
solution
neutral
solution
[H+] < [OH-]
basic
solution

6. Soren Sorensen
(1868 - 1939)
The pH scale was invented by the Danish chemist
Soren Sorensen to measure the acidity of beer in a
brewery. The pH scale measured the concentration of
hydrogen ions in solution. The more hydrogen ions,
the stronger the acid.

7. 1
2
Strong
Acid
3
4
Weak
Acid
5
6
7
Neutral
8
9
10
11
Weak
Alkali
12
13
14
Strong
Alkali

8. The amount of hydrogen ions in
solution can affect the color of
certain dyes found in nature. These
dyes can be used as indicators to
test for acids and alkalis.
An
indicator such as litmus (obtained
from lichen) is red in acid. If base is
slowly added, the litmus will turn
blue when the acid has been
neutralized, at about 6-7 on the pH
scale. Other indicators will change
color at different pH’s.
A
combination of indicators is used to
make a universal indicator.

9. Measuring pH
Universal Indicator Paper
Universal Indicator Solution
pH meter

10. Measuring pH
 pH can be measured in several ways
 Usually it is measured with a coloured acid-base
indicator or a pH meter
 Coloured indicators are a crude measure of pH, but are
useful in certain applications
 pH meters are more accurate, but they must be
calibrated prior to use
 Calibration means setting to a standard
 A pH meter is calibrated with a solution of known pH
often called a buffer
 “Buffer” indicates that the pH is stable

11. Limitations of pH Scale
The pH scale ranges from 0 to 14
Values outside this range are possible but do not
tend to be accurate because even strong acids and
bases do not dissociate completely in highly
concentrated solutions.
pH is confined to dilute aqueous solutions

12. At 250C
Kw = 1 x 10-14 mol2/litre2
[H+ ] x [OH- ] = 1 x 10-14 mol2/litre2
This equilibrium constant is very important because it
applies to all aqueous solutions - acids, bases, salts,
and non-electrolytes - not just to pure water.

13. For H2O(l) ⇄
H+(aq) + OH-(aq)
→
[H+ ] =
[H+ ] x [OH- ] = 1 x 10-14
[OH- ]
= [1 x 10-7 ] x [1 x 10-7 ]
[H+ ] of water is at 250C is 1 x 10-7 mol/litre
Replacing [H+ ] with pH to indicate acidity of solutions
pH 7 replaces [H+ ] of 1 x 10-7 mol/litre
where
pH =
- Log10 [H+ ]

14. T (°C)
pH
0
7.12
10
7.06
20
7.02
25
7
30
6.99
40
6.97
pH of pure water decreases as the temperature increases
A word of warning!
If the pH falls as temperature increases, does this mean that water
becomes more acidic at higher temperatures?
NO!
Remember a solution is acidic if there is an excess of hydrogen ions over hydroxide ions.
In the case of pure water, there are always the same number of hydrogen ions and hydroxide
ions. This means that the water is always neutral - even if its pH change

15. Acid – Base Concentrations and pH
concentration (moles/L)
10-1
pH = 11
pH = 3
OH-
H+
pH = 7
10-7
H+
OH-
OH-
H+
10-14
[H3O+] > [OH-]
acidic
solution
[H3O+] = [OH-]
neutral
solution
[H3O+] < [OH-]
basic
solution

16. pH describes both [H+ ] and [OH- ]
0
Acidic [H+ ] = 100
[OH- ] =10-14
pH
Neutral
[H+ ] = 10-7
[OH- ] =10-7
pH
Basic
[H+ ] = 10-14
pH
= 14
= 0
= 7
[OH- ] = 100

17. 

18. pH of Common Substances
Acidic
Neutral
Basic

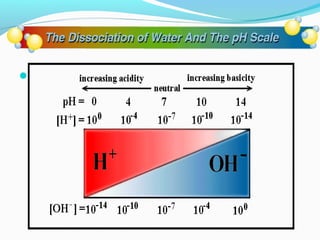
19. More acidic
More basic
pH
NaOH, 0.1 M
Household bleach
Household ammonia
Lime water
Milk of magnesia
Borax
Baking soda
Egg white, seawater
Human blood, tears
Milk
Saliva
Rain
Black coffee
Banana
Tomatoes
Wine
Cola, vinegar
Lemon juice
Gastric juice
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
[H+]
[OH-]
pOH
1 x 10-14
1 x 10-13
1 x 10-12
1 x 10-11
1 x 10-10
1 x 10-9
1 x 10-8
1 x 10-7
1 x 10-6
1 x 10-5
1 x 10-4
1 x 10-3
1 x 10-2
1 x 10-1
1 x 100
1 x 10-0
1 x 10-1
1 x 10-2
1 x 10-3
1 x 10-4
1 x 10-5
1 x 10-6
1 x 10-7
1 x 10-8
1 x 10-9
1 x 10-10
1 x 10-11
1 x 10-12
1 x 10-13
1 x 10-14
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14

20. Calculations and practice
• You will need to memorize the following:
[H+] = 10–pH
[OH–] = 10–pOH
pH = – log10[H+]
pOH = – log10[OH–]
pH + pOH = 14

21. pH Calculations
pH
pH = -log10[H+]
[H+]
[H+] = 10-pH
pH + pOH = 14
pOH
[H+] [OH-] = 1 x10-14
pOH = -log10[OH-]
[OH-] = 10-pOH
[OH-]

22. pH for Strong Acids
Strong acids dissociate completely in solution
Strong bases also dissociate completely in solution

23. pH Exercises
a) pH of 0.02M HCl
pH = – log10 [H+]
= – log10 [0.020]
= 1.6989
= 1.70
b) pH of 0.0050M NaOH
pOH = – log10 [OH–]
= – log10 [0.0050]
= 2.3
pH
= 14 – pOH
= 14 – 2.3
=11.7
c) pH of solution where [H +]
is 7.2x10-8M
pH
= – log10 [H+]
= – log10 [7.2x10-8]
= 7.14
(slightly basic)

24. monoprotic
e.g. HCl, HNO3
HA(aq)
0.3 M
H1+(aq) + A1-(aq)
0.3 M
0.3 M
pH = ?
pH = - log10 [H+]
pH = - log10[0.3M]
pH =
diprotic
e.g. H2SO4
H2A(aq)
0.3 M
2 H1+(aq) + A2-(aq)
0.6 M
0.3 M
0.48
pH = - log10[H+]
pH = - log10[0.6M]
pH =
0.78

25. A sample of orange juice has a hydrogen-ion
concentration of 2.9 x 10-4M. What is the pH?
pH = -log10 [H+ ]
pH = -log10 (2.9x10-4 )
pH = 3.54

26. Given: pH = 4.6
determine the [hydrogen ion]
pH = - log10 [H+]
choose proper equation
4.6 = - log10 [H+]
substitute pH value in equation
- 4.6 =
2nd
log
log10[H+]
multiply both sides by -1
- 4.6 =
antilog [H+]
take antilog of both sides
[H+] = 2.51x10-5 M
10x
antilog
You can check your answer by working backwards.
pH = - log10[H+]
pH = - log10[2.51x10-5 M]
pH = 4.6

27. Most substances that are acidic in water are actually weak acids.
Because weak acids dissociate only partially in aqueous solution,
an equilibrium is formed between the acid and its ions.
The ionization equilibrium is given by:
HX(aq)
where X- is the conjugate base.
H+(aq) + X-(aq)

28. For Weak Acids
pH = -Log10
For Weak Bases
pOH = Log10
pH =
14 - pOH

29. pH of solutions of weak concentrations
Weak Acid
pH of a 1M solution of ethanoic acid with a Ka value of 1.8 x 10-5
pH = -Log10
pH = -Log10
pH = 2.3723

30. pH of solutions of weak concentrations
Weak Base
pH of a 0.2M solution of ammonia with a Kb value of 1.8 x 10-5
pOH = -log10
pOH = -log10
pOH = 2.7319
pH = 14 – 2.7319
pH = 11.2681

31. Theory of Acid Base Indicators
Acid-base titration indicators are quite often weak acids.
For the indicator HIn
The equilibrium can be simply expressed as
HIn(aq, colour 1)
H+(aq) + In-(aq, colour 2)

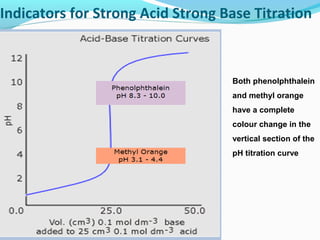
32. Theory of Acid Base Indicators
Applying Le Chatelier's equilibrium principle:
Addition of acid
•
favours the formation of more HIn (colour 1)
HIn(aq)
H+(aq) + In-(aq)
because an increase on the right of [H+]
causes a shift to left
increasing [HIn] (colour 1)
to minimise 'enforced' rise in [H+].

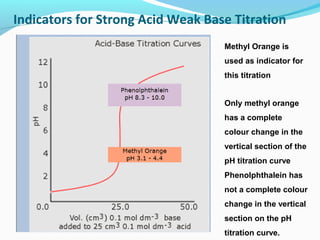
33. Theory of Acid Base Indicators
Applying Le Chatelier's equilibrium principle:
Addition of base
•
favours the formation of more In- (colour 2)
HIn(aq)
H+(aq) + In-(aq)
The increase in [OH-] causes a shift to right
because the reaction
H+(aq) + OH-(aq) ==> H2O(l)
Reducing the [H+] on the right
so more HIn ionises to replace the [H+]
and so increasing In- (colour 2)
to minimise 'enforced' rise in [OH-]

34. Theory of Acid Base Indicators
Acid-base titration indicators are also often weak bases.
For the indicator MOH
The equilibrium can be simply expressed as
MOH(aq, colour 1)
OH-(aq) + M+(aq, colour 2)

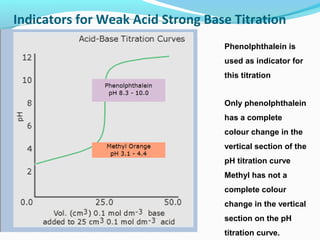
35. Theory of Acid Base Indicators
Applying Le Chatelier's equilibrium principle:
Addition of base
•
favours the formation of more MOH (colour 1)
MOH(aq)
M+(aq) + OH-(aq)
because an increase on the right of [OH-]
causes a shift to left
increasing [MOH] (colour 1)
-
to minimise 'enforced' rise in [OH ].

36. Theory of Acid Base Indicators
Applying Le Chatelier's equilibrium principle:
Addition of acid
•
favours the formation of more M+ (colour 2)
MOH(aq)
M+(aq) + OH-(aq)
The increase in [H+] causes a shift to right
because the reaction
H+(aq) + OH-(aq) ==> H2O(l)
Reducing the [OH-] on the right
so more MOH ionises to replace the [OH-]
and so increasing M+ (colour 2)
+

37. Acid Base Titration Curves
Strong Acid – Strong Base
Weak Acid – Strong Base
Strong Acid – Weak Base
Weak Acid – Weak Base

38. Choice of Indicator for Titration
Indicator must have a complete colour change in
the vertical part of the pH titration curve
Indicator must have a distinct colour change
Indicator must have a sharp colour change

39. Indicators for Strong Acid Strong Base Titration
Both phenolphthalein
and methyl orange
have a complete
colour change in the
vertical section of the
pH titration curve

40. Indicators for Strong Acid Weak Base Titration
Methyl Orange is
used as indicator for
this titration
Only methyl orange
has a complete
colour change in the
vertical section of the
pH titration curve
Phenolphthalein has
not a complete colour
change in the vertical
section on the pH
titration curve.

41. Indicators for Weak Acid Strong Base Titration
Phenolphthalein is
used as indicator for
this titration
Only phenolphthalein
has a complete
colour change in the
vertical section of the
pH titration curve
Methyl has not a
complete colour
change in the vertical
section on the pH
titration curve.

42. Indicators for Weak Acid Weak Base Titration
No indicator suitable
for this titration
because no vertical
section
Neither phenolphthalein
nor methyl orange have
completely change colour
in the vertical section on
the pH titration curve

43. indicator
pH range
litmus
5-8
methyl orange
3.1 - 4.4
phenolphthalein
8.3 - 10.0

44. Colour Changes and pH ranges

45. Universal indicator components
Indicator
Low pH color
Thymol blue (first transition)
red
1.2–2.8
orange
Methyl Orange
red
4.4–6.2
yellow
Bromothymol blue
yellow
6.0–7.6
blue
Thymol blue (second transition) yellow
8.0–9.6
blue
Phenolphthalein
8.3–10.0
purple
colourless
Transition pH range
High pH color