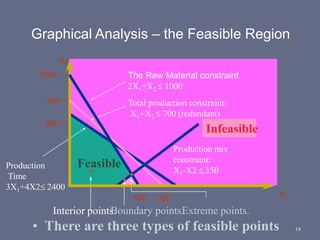
Linear programming is a mathematical modeling technique used to determine optimal resource allocation to achieve objectives. It involves converting a problem into a linear mathematical model with decision variables, constraints, and an objective function. The optimal solution is found by systematically increasing the objective function value until infeasibility is reached. For example, a linear programming model was used to determine the optimal production mix and levels of two drug combinations to maximize profit given resource constraints. The optimal solution was found to be 320 dozen of drug X1 and 360 dozen of drug X2, utilizing all available resources and achieving $4,360 in weekly profit.

1. Linear Programming
Dr Ravindra Singh

2. Contents
• Introduction
• History
• Applications
• Linear programming model
• Example of Linear Programming Problems
• Graphical Solution to Linear Programming
Problem
• Sensitivity analysis
2

3. Introduction
• Linear Programming is a mathematical modeling
technique used to determine a level of operational
activity in order to achieve an objective.
• Mathematical programming is used to find the best or
optimal solution to a problem that requires a decision or
set of decisions about how best to use a set of limited
resources to achieve a state goal of objectives.
3

4. • Steps involved in mathematical programming
– Conversion of stated problem into a mathematical model that
abstracts all the essential elements of the problem.
– Exploration of different solutions of the problem.
– Find out the most suitable or optimum solution.
• Linear programming requires that all the mathematical
functions in the model be linear functions.
4

5. LP Model Formulation
• Decision variables
– mathematical symbols representing levels of activity of an operation
• Objective function
– a linear relationship reflecting the objective of an operation
– most frequent objective of business firms is to maximize profit
– most frequent objective of individual operational units (such as a
production or packaging department) is to minimize cost
• Constraint
– a linear relationship representing a restriction on decision making
5

6. History of linear programming
• It started in 1947 when G. B. Dantzig design the
“simplex method” for solving linear programming
formulations of U.S. Air Force planning problems.
• It soon became clear that a surprisingly wide range of
apparently unrelated problems in production
management could be stated in linear programming
terms and solved by the simplex method.
6

7. Applications
The Importance of Linear Programming
• Hospital management
• Diet management
• Manufacturing
• Finance (investment)
• Advertising
• Agriculture
7

8. 8
The Galaxy Industries Production Problem
• Galaxy manufactures two drug combination
of same drug:
– X1
– X2
• Resources are limited to
– 1000 pounds raw material.
– 40 hours of production time per week.

9. 9
• Marketing requirement
– Total production cannot exceed 700 dozens.
– Number of dozens of X1cannot exceed number
of dozens of X2 by more than 350.
• Technological input
– X1 requires 2 pounds of raw material and
3 minutes of labor per dozen.
– X2 requires 1 pound of raw material and
4 minutes of labor per dozen.
The Galaxy Industries Production Problem

10. 10
• The current production plan calls for:
– Producing as much as possible of the more profitable
product, X1 ($8 profit per dozen).
– Use resources left over to produce X2 ($5 profit
per dozen), while remaining within the marketing
guidelines.
• The current production plan consists of:
X1 = 450 dozen
X2 = 100 dozen
Profit = $4100 per week
The Galaxy Industries Production Problem
8(450) + 5(100)

11. 11
Management is seeking a
production schedule that
will increase the company’s
profit.

12. 12
• Decisions variables:
– X1 = Weekly production level of X1 (in dozens)
– X2 = Weekly production level of X2 (in dozens).
• Objective Function:
– Weekly profit, to be maximized
The Galaxy Linear Programming Model

13. 13
Max 8X1 + 5X2 (Weekly profit)
subject to
2X1 + 1X2 1000 (Raw Material)
3X1 + 4X2 2400 (Production Time)
X1 + X2 700 (Total production)
X1 - X2 350 (Mix)
Xj> = 0, j = 1,2 (Non negativity)
The Galaxy Linear Programming Model

14. 14
The Graphical Analysis of Linear
Programming
The set of all points that satisfy all
the constraints of the model is called
a
FEASIBLE REGION

15. 15
Using a graphical presentation
we can represent all the constraints,
the objective function, and the three
types of feasible points.

16. 16
The non-negativity constraints
X2
X1
Graphical Analysis – the Feasible Region

17. 17
1000
500
Feasible
X2
Infeasible
Production
Time
3X1+4X2 2400
Total production constraint:
X1+X2 700 (redundant)
500
700
The Raw material constraint
2X1+X2 1000
X1
700
Graphical Analysis – the Feasible Region

18. 18
1000
500
Feasible
X2
Infeasible
Production
Time
3X1+4X2 2400
Total production constraint:
X1+X2 700 (redundant)
500
700
Production mix
constraint:
X1-X2 350
The Raw Material constraint
2X1+X2 1000
X1
700
Graphical Analysis – the Feasible Region
• There are three types of feasible points
Interior points.Boundary points.Extreme points.

19. 19
The search for an optimal solution
Start at some arbitrary profit, say profit = $2,000...
Then increase the profit, if possible...
...and continue until it becomes infeasible
Profit
=$4360500
700
1000
500
X2
X1

20. 20
Summary of the optimal solution
X1 = 320 dozen
X2 = 360 dozen
Profit = $4360
– This solution utilizes all the plastic and all the production
hours.
– Total production is only 680 (not 700).
– X1 production exceeds X2 production by only 40 dozens.

21. 21
– If a linear programming problem has an
optimal solution, an extreme point is optimal.
Extreme points and optimal solutions

22. 22
• For multiple optimal solutions to exist, the
objective function must be parallel to one of the
constraints
Multiple optimal solutions
•Any weighted average of
optimal solutions is also an
optimal solution.

23. 23
Sensitivity Analysis of the Optimal Solution
• Is the optimal solution sensitive to changes in
input parameters?
• Possible reasons for asking this question:
– Parameter values used were only best estimates.
– Dynamic environment may cause changes.
– “What-if” analysis may provide economical and
operational information.

24. 24
• Range of Optimality
– The optimal solution will remain unchanged as long as
• An objective function coefficient lies within its range of
optimality
• There are no changes in any other input parameters.
– The value of the objective function will change if the
coefficient multiplies a variable whose value is
nonzero.
Sensitivity Analysis of
Objective Function Coefficients.

25. 25

26. REFERENCES
• www.math.ucla.edu/~tom/LP.pdf
• www.sce.carleton.ca/faculty/chinneck/po/Chapter2.
• www.markschulze.net/LinearProgramming.pdf
• web.ntpu.edu.tw/~juang/ms/Ch02.
• cmp.felk.cvut.cz/~hlavac/Public/.../Linear%20Progra
mming-1.ppt
• www.slideshare.net/nagendraamatya/linear-
programming
26

27. 27