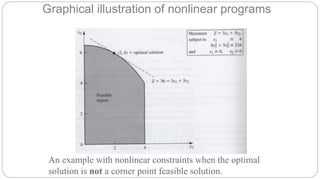
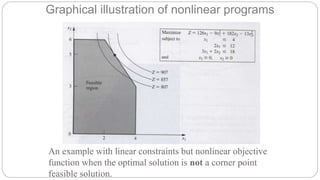
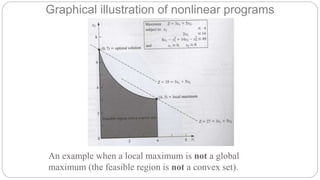
This document discusses nonlinear programming (NLP) problems. NLP problems involve objective functions and/or constraints that contain nonlinear terms, making them more difficult to solve than linear programs. While exact solutions cannot always be found, algorithms can typically find approximate solutions within an acceptable error range of the optimum. However, for some NLP problems there is no reliable way to find the global maximum, as algorithms may stop at a local maximum instead. The document describes different types of NLP problems and techniques for solving them, including using Excel Solver with multiple starting values to attempt finding the global rather than just local optima.

1. Session 3
Reading: IOR Ch. 12.1-12.5
Quantitative Techniques in Management - II

2. Nonlinear Programming (NLP)
 NLP problems take the general form of LP problems, except the
objective function and/or the constraint contain non-linear terms.
 It is generally very difficult to find an exact solution to NLP
problems. The various algorithms generally reach an approximate
solution within a certain acceptable error of the optimum.
 Some NLP problems, there is no reliable way to find the global
maxima, existing algorithms often stop after reaching a local
maxima.
 Real-life applications include – (a) Product-mix problems with price
elasticity (b) Transportation problem with volume discounts (c)
Minimizing risk with risky securities.
 Whether the objective function f(x) or the constraints g(x) are
nonlinear, and how, leads to different types of NLP problems, each

3. Graphical illustration of nonlinear programs
An example with nonlinear constraints when the optimal
solution is not a corner point feasible solution.

4. Graphical illustration of nonlinear programs
An example with linear constraints but nonlinear objective
function when the optimal solution is not a corner point
feasible solution.

5. Graphical illustration of nonlinear programs
An example when a local maximum is not a global
maximum (the feasible region is not a convex set).

6. Types of NLP problems
 Unconstrained optimization: min or max
f(x1,…,xn), no functional constraints.
 Linearly constrained optimization
 Objective function nonlinear
 Functional constraints linear
Extensions of simplex method can be applied.
 Quadratic programming
Special case of linearly constrained optimization when
the objective function is quadratic.
 Convex programming
 Objective function f is concave and each constraint gi is
convex
- Covers a broad class of problems.
- A local maximum is a global maximum

7.  Separable programming
 A special case of convex programming when f and gi are separable
functions. In a separable function each term involves just a single
variable.
 E.g., f(x1, x2) = x1
2 + 2x1- 4x2
2 + 3x2,
 Can be closely approximated by a linear programming problem.
 Nonconvex programming
 Even if we are successful in finding a local maximum, there is no
assurance that it also will be a global maximum.
 In some special cases (Geometric programming, Fractional
programming), the problem can be reduced to an equivalent convex
programming problem.
 In fractional programming, when both numerator and denominator
are linear functions, it can be transformed into an LP problem.

8. Single-variable unconstrained optimization
 Objective is to maximize (or minimize) a non-linear function with a
single variable f(x) with no other constraints.
 If f(x) is sufficiently simple, then we solve the equation
𝑑𝑓
𝑑𝑥
= 0. This
method is only usable if
𝑑𝑓
𝑑𝑥
is a linear or quadratic function, as
otherwise it may not be possible to solve the equation.

9. 9
Fixed cost (cf = $7,500) and variable cost per unit (cv =$40);
Price per unit p, Demand V=400-1.2p, maximize profit.
Furniture Company Problem (simpler f(x) function)
(See “QTM 2 Session 3” for excel solution)
Profit, Z = V*p-cf-V*cv,
Z = 448p – 1.2p2 -23,500
dZ/dp = 448 – 2.4p= 0
p = 448/2.4
= $186.66
V = 400 – 1.2p = 175.996
chairs
Z = $18,313.87

10.  A manufacturing plant has a cost per unit of manufacturing a
product as 40 +
(20 − 0.06𝑥)2
𝑤ℎ𝑒𝑟𝑒 𝑥 𝑖𝑠 𝑡ℎ𝑒 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑢𝑛𝑖𝑡𝑠 𝑚𝑎𝑛𝑢𝑓𝑎𝑐𝑡𝑢𝑟𝑒𝑑,
and a fixed cost of Rs. 5000.
 The demand follows the function 5000-16p where p is the selling
price per unit.
 What is the maximum profit? Assume manufactured supply equals
demand.
Profit Z
 𝑀𝑎𝑥 𝑍 = 𝑝 5000 − 16𝑝 − 5000 − (40 +
(20 − 0.06 5000 − 16𝑝 )2)(5000 − 16𝑝)
 𝑝 ≥ 0, 5000 ≥ 16𝑝

11.  General NLP problems are solved using Excel Solver
 General NLP problems often have local optima.
 One way to find global optima instead of local optima is to use multiple
starting values for the decision variables when using Excel solver
 This can be done by manually entering different starting values for the
variables before hitting the ‘solve’ button, or using the ‘Multi Start’ option
in the advanced options of Solver.
 This is not a perfect solution, but should be attempted in any general
NLP problem.