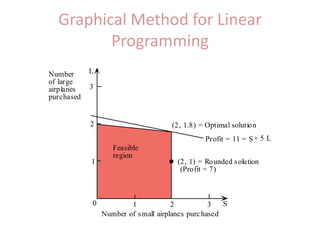
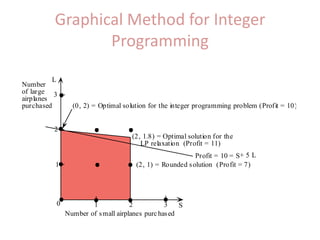
Kingfisher Airlines was considering expanding its operations by purchasing additional small or large planes. Using linear programming, the optimal solution was to purchase a non-integer number of planes. However, fractional planes cannot be purchased, so a new integer programming model was developed. This model was solved graphically by finding the last integer point within the feasible region that the objective function line passes through, which provides the optimal number of small and large planes to purchase.

1. NehaNimbekarR750209011MBA(ISM)Linear Programming

2. Kingfisher AirlinesEarlier Kingfisher Airlines was a small company that uses small planes for short flights.The company was considering to expand its operations.Kingfisher has two choices:Buy more small planes (SP) and continue with short flightsBuy only large planes (LP) and only expand into larger markets with longer flightsExpand by purchasing some small and some large planes

3. Kingfisher Airlines Cont.Question: How many large and small planes should be purchased to maximize total net annual profit?

4. Kingfisher Airlines

5. Mathematical Model for Kingfisher

6. Graphical Method for Linear Programming

7. Divisibility Assumption of LPThis assumption says that the decision variables in a LP model are allowed to have any values that satisfy the functional and non-negativity constraints. This implies that the decision variables are not restricted to integer values. Note: Implicitly in Kingfisher’s problem, it cannot purchase a fraction of a plane which implies this assumption is not met.

8. New Mathematical Model for Kingfisher

9. The Graphical Solution Method For Integer ProgrammingStep 1: Graph the feasible regionStep 2: Determine the slope of the objective function lineStep 3: Moving the objective function line through this feasible region in the direction of improving values of the objective function.Step 4: Stop at the last instant the the objective function line passes through an integer point that lies within this feasible region.This integer point is the optimal solution.

10. Graphical Method for Integer Programming

11. Thank You