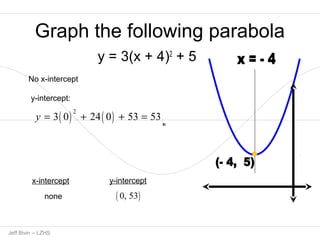
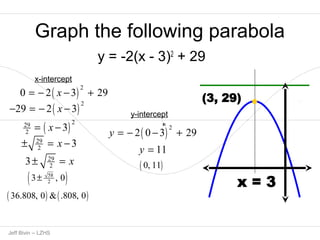
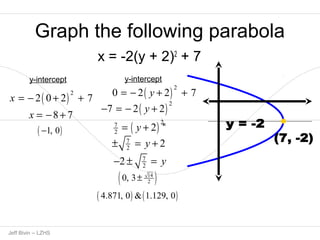
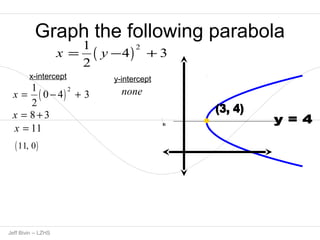
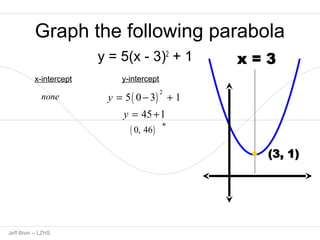
1. The document contains step-by-step solutions for graphing 12 different parabolas of the form y=ax^2+bx+c. 2. For each parabola, the key steps shown are completing the square, determining the axis of symmetry and vertex, and finding any x-intercepts or the y-intercept. 3. The graphs are noted as opening up, down, left or right based on the sign of the leading coefficient a.

1. 1p JLeafsf t BUivpidna -t-e LdZ: H ASpril 7, 2011
By: Jeffrey Bivin
Lake Zurich High School
jeff.bivin@lz95.org

2. Graph the following parabola
y = 3x2 + 24x + 53
y = 3(x2 + 8x ) + 53
y + 48 = 3(x2 + 8x + (4)2) + 53
y = 3(x2 + 8x + (4)2) + 53 - 48
3●(4)2 = 48
1p Jeff Bivin -- LZHS
y = 3(x + 4)2 + 5
x + 4 = 0
Axis of symmetry: x = -4
Vertex: (-4, 5)
Note: opens up

3. Graph the following parabola
y = 3(x + 4)2 + 5
No x-intercept
y-intercept:
y = 3( 0) 2 + 24( 0) + 53 = 53
1p x-intercept
y-intercept
none
( 0, 53)
Jeff Bivin -- LZHS

4. Graph the following parabola
y = -2x2 + 12x + 11
y = -2(x2 - 6x ) + 11
-2●(-3)2 = -18
y - 18 = -2(x2 - 6x + (-3)2) + 11
y = -2(x2 - 6x + (-3)2) + 11 + 18
1p Jeff Bivin -- LZHS
y = -2(x - 3)2 + 29
x - 3 = 0
Axis of symmetry: x = 3
Vertex: (3, 29)
Note: opens down

5. Graph the following parabola
y = -2(x - 3)2 + 29
x-intercept
y-intercept
1p Jeff Bivin -- LZHS
y = - 2( 0 - 3) 2 + 29
( 0, 11)
( ) 2 0 = - 2 x -3 + 29
( ) 2 -29 = - 2 x - 3
( ) 29 2
2 = x - 3
29
2 ± = x - 3
3± 29
= x
2 ( 3± 58 , 0
)
2 ( 36.808, 0) &( .808, 0)
y = 11

6. Graph the following parabola
x = -2y2 - 8y - 1
x = -2(y2 + 4y ) - 1
x - 8 = -2(y2 + 4y + (2)2) - 1
x = -2(y2 + 4y + (2)2) - 1 + 8
-2(2)2 = -8
1p Jeff Bivin -- LZHS
x = -2(y + 2)2 + 7
y + 2 = 0
Axis of symmetry: y = -2
Vertex: (7, -2)
Note: opens left

7. Graph the following parabola
x = -2(y + 2)2 + 7
y-intercept y-intercept
( ) 2 x = - 2 0 + 2 + 7
( -1, 0)
1p Jeff Bivin -- LZHS
( ) 2 0 = - 2 y + 2 + 7
( ) 2 -7 = - 2 y + 2
( ) 7 2
2 = y + 2
7
2 ± = y + 2
-2 ± 7
= y
2 ( 0, 3±
14 )
2 ( 4.871, 0) &(1.129, 0)
x = -8 + 7

8. Graph the following parabola
1
x = y2 - 4y + 11
2
x = 1
(y2 - 8y ) + 11
2
1
x + 8 = (y2 - 8y + (-4)2) + 11
2
1
x = (y2 - 8y + (-4)2 2 ) + 11 - 8
1 =
(16) 8
2
1p 1
Jeff Bivin -- LZHS
x = (y - 4)2 + 3
2
y - 4 = 0
Axis of symmetry: y = 4
Vertex: (3, 4)
Note: opens right

9. Graph the following parabola
1 ( 4)2 3
2
x = y - +
x-intercept y-intercept
( ) 1 0 4 2 3
2
x = - +
1p (11, 0)
Jeff Bivin -- LZHS
none
x = 8 + 3
x = 11

10. Graph the following parabola
x = y2 + 10y + 8
x = (y2 + 10y ) + 8
x + 25 = (y2 + 10y + (5)2) + 8
x = (y2 + 10y + (5)2) + 8 - 25
(5)2 = 25
1p Jeff Bivin -- LZHS
x = (y + 5)2 - 17
y + 5 = 0
Axis of symmetry: y = -5
Vertex: (-17, -5)
Note: opens right

11. Graph the following parabola
x = (y + 5)2 - 17
x-intercept y-intercept
( ) 2 x = 0 + 5 - 17
1p ( 8, 0)
Jeff Bivin -- LZHS
( ) 2 0 = y + 5 - 17
( ) 2 17 = y + 5
± 17 = y + 5
-5 ± 17 = y
( 0, -5 ± 17 )
( -0.877, 0) &( -9.123, 0)
x = 25 -17
x = 8

12. Graph the following parabola
y = 5x2 - 30x + 46
y = 5(x2 - 6x ) + 46
5●(-3)2 = 45
y + 45 = 5(x2 - 6x + (-3)2) + 46
y = 5(x2 - 6x + (-3)2) + 46 - 45
1p Jeff Bivin -- LZHS
y = 5(x - 3)2 + 1
x - 3 = 0
Axis of symmetry: x = 3
Vertex: (3, 1)
Note: opens up

13. Graph the following parabola
y = 5(x - 3)2 + 1
x-intercept y-intercept
y = 5( 0 - 3) 2 + 1
y = 45 +1
( 0, 46)
none
1p Jeff Bivin -- LZHS