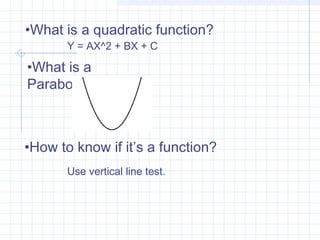
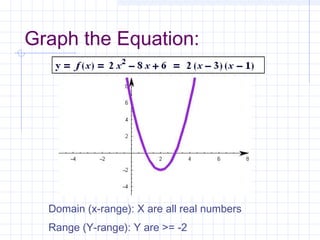
This document discusses how to solve and graph quadratic equations. It explains that a quadratic function has the form y=ax^2 + bx + c, and that the graph of a quadratic function is a parabola. It provides steps to find the x-intercepts, y-intercept, vertex, and determine if a parabola opens up or down by analyzing the leading coefficient a. Examples are given to demonstrate how to apply these steps to solve and graph specific quadratic equations.

1. Solve and Graph Quadratic
Equation
Algebra II

2. What Shape is the Golden Gate Bridge?

3. •What is a quadratic function?
Y = AX^2 + BX + C
•What is a
Parabola?
•How to know if it’s a function?
Use vertical line test.

4. How to find X-intercepts?
X-intercepts: also known as roots, are
the locations where the graph
intersects with the X-axis.
Example: Y = 2X^2 – 8X + 6
Let Y = 0, solve for X:
2X^2 – 8X + 6 = 0
X^2 – 4X + 3 = 0 (simplify)
(X-1)(X-3) = 0 (factor it)
X=1, or X=3

5. How to find Y-intercepts?
Y-intercept: the location where the
graph intersects with the Y-axis.
Example: Y = 2X^2 – 8X + 6
Let 0 = 0, solve for Y:
Y = 2(0)^2 – 8(0) + 6
Y = 0 – 0 + 6 (simplify)
Y=6 (simplify)

6. How to find vertex?
Vertex: the lowest or highest point of the graph.
Example: Y = 2X^2 – 8X + 6, (a=2, b=-8, c=6)
Formula for vertex X= -b/(2a)
X = -(-8)/(2*2)
X = 8/4 = 2 (simplify)
When X=2, Y=2(2)^2-8(2)+6 =8-16+6 =-2
So vertex is (2, -2)

7. How to determine the direction of a
parabola’s opening?
When a>0, parabola opens up
When a<0, parabola opens down
Example: Y = 2X^2 – 8X + 6, (a=2)
Because 2>0, the parabola opens up

8. Graph the Equation:
Domain (x-range): X are all real numbers
Range (Y-range): Y are >= -2