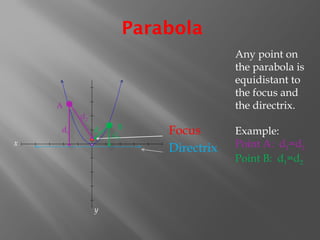
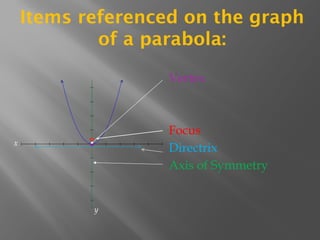
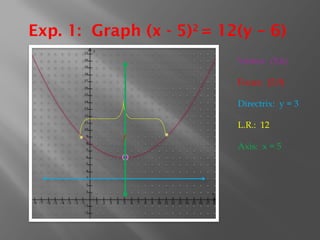
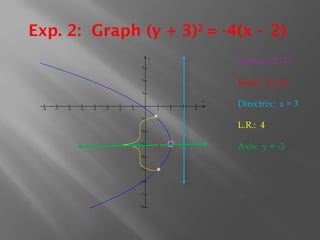
The document discusses the geometric and algebraic definitions of parabolas, including their properties, equations, and steps for graphing them. It provides examples of graphing parabolas, illustrating how to identify key features such as the vertex, focus, directrix, and axis of symmetry. Additionally, the document addresses common errors in graphing and provides a challenge question related to parabolas.

1. CONIC SECTIONS:
THE PARABOLA

2. Parabola
 Review: The geometric definition relies on a
cone and a plane intersecting it.
 Algebraic definition: All points that are
equidistant from a given line (the directrix)and
a fixed point not on the directrix (the focus)

3. Parabola
Focus
Directrix
x
y
Any point on
the parabola is
equidistant to
the focus and
the directrix.
Example:
Point A: d1=d2
Point B: d1=d2
A
d1
d2
d1
d2
B

4. Items referenced on the graph
of a parabola:
Vertex
Focus
Directrix
Axis of Symmetry
x
y

5. Facts: Parabola Equations
 One variable is squared and one is not. (How
does this differ from linear equations?)
 There are many ways the equation of a
parabola can be written. We will get the
quadratic part (variable that is squared) on the
left of the equal sign and the linear part
(variable is to the first power) on the right of
the equal sign.
 Equation:
(x - h)2
= 4p(y – k) OR (y - k)2
= 4p(x – h)

6. (x - h)2
= 4p(y – k) OR (y - k)2
= 4p(x – h)
where the vertex is at (h,k) and |4p| is the width at the focus
To graph:
1. Put in standard form (above) – squared term on left
2. Decide which way the parabola opens.
Look at the right side. If y: + p → opens up
If y: - p → opens down
If x: + p → opens right
If x: - p → opens left

7. (x - h)2
= c(y – k) OR (y - k)2
= c(x – h)
where the vertex is at (h,k) and |4p| is the
width at the focus
To graph:
3. Plot the vertex (h,k) Note what happens to the
signs.
4. Plot the focus: move │p│ from the vertex in
the direction that the parabola opens. Mark
with an f.
5. Draw the directrix: │p│ from the vertex in the
opposite direction of the focus (Remember that
the directrix is a line.)

8. (x - h)2
= c(y – k) OR (y - k)2
= c(x – h)
where the vertex is at (h,k) and |4p| is the
width at the focus
To graph:
6. Plot the endpoints of the latus rectum/focal
chord (width at the focus). The width is the
│4p│ at the focus.
7. Sketch the parabola by going through the
vertex and the endpoints of the latus rectum.
(Be sure to extend the curve and put arrows.)
8. Identify the axis of symmetry. (The line that
goes through the vertex dividing the parabola
in half.)

9. Exp. 1: Graph (x - 5)2
= 12(y – 6)
To graph:
1. Put in standard form– squared term on left
Done
2. Decide which way the parabola opens.
Look at the right side. If y: + p → opens up
If y: - p → opens down
If x: + p → opens right
If x: - p → opens left
Up because y is on the right and 3 is positive

10. Exp. 1: Graph (x - 5)2
= 12(y – 6)
To graph:
3. Plot the vertex (h,k) Note what happens to the signs.
(5,6)
4. Plot the focus: move │p│ from the vertex in the
direction that the parabola opens. Mark with an f.
(5,9): found by moving up 3 from the vertex
5. Draw the directrix: │p│ from the vertex in the
opposite direction of the focus (Remember that the
directrix is a line.)
y = 3: found by moving down 3 from the vertex

11. Exp. 1: Graph (x - 5)2
= 12(y – 6)
To graph:
6. Plot the endpoints of the latus rectum/focal chord
(width at the focus). The width is the │4p│ at the
focus.
L.R. = 12 with endpoints at (-1,9) & (11,9)
7. Sketch the parabola by going through the vertex and
the endpoints of the latus rectum. (Be sure to extend
the curve and put arrows.)
8. Identify the axis of symmetry. (The line that goes
through the vertex dividing the parabola in half.)
x = 5

12. Exp. 1: Graph (x - 5)2
= 12(y – 6)
                                 
 
 





















x
y
Vertex: (5,6)
Focus: (5,9)
Directrix: y = 3
L.R.: 12
Axis: x = 5
f

13. Exp. 2: Graph (y + 3)2
= -4(x – 2)
To graph:
1. Put in standard form
Done
2. Decide which way the parabola opens.
Left because x is on the right and 4 is negative
3. Plot the vertex (h,k)
(2,-3)
4. Plot the focus:
(1,-3): found by moving left 1 from the vertex
5. Draw the directrix:
x = 3: found by moving right 1 from the vertex

14. Exp. 2: Graph (y + 3)2
= -4(x – 2)
To graph:
6. Plot the endpoints of the latus rectum
L.R. = 4 with endpoints at (1,-1) & (1,-5)
7. Sketch the parabola
8. Identify the axis of symmetry.
y = -3

15.                    
 
 
 
 
 
 
 
 



x
y
Exp. 2: Graph (y + 3)2
= -4(x – 2)
Vertex: (2,-3)
Focus: (1,-3)
Directrix: x = 3
L.R.: 4
Axis: y = -3
f

16. Exp. 1: Graph x = y2
- 4y + 1
 What’s the first step?
Put in standard form.
y2
- 4y + 1 = x
y2
- 4y + 4 = x - 1 + 4 Complete the square.
(y – 2)2
= x + 3
(y – 2)2
= 1(x + 3)
 Now you try graphing the parabola and labeling
all the parts.

17. Challenge Question
Given the following information, write the
equation of the parabola.
Vertex is (0,0) and Focus is at (0,2)

18. Review
1) How can you tell the graph of an equation will
be a parabola?
2) What’s the standard form of a parabola?
3) What are the steps for graphing a parabola?
4) What are common errors people make when
graphing parabolas?