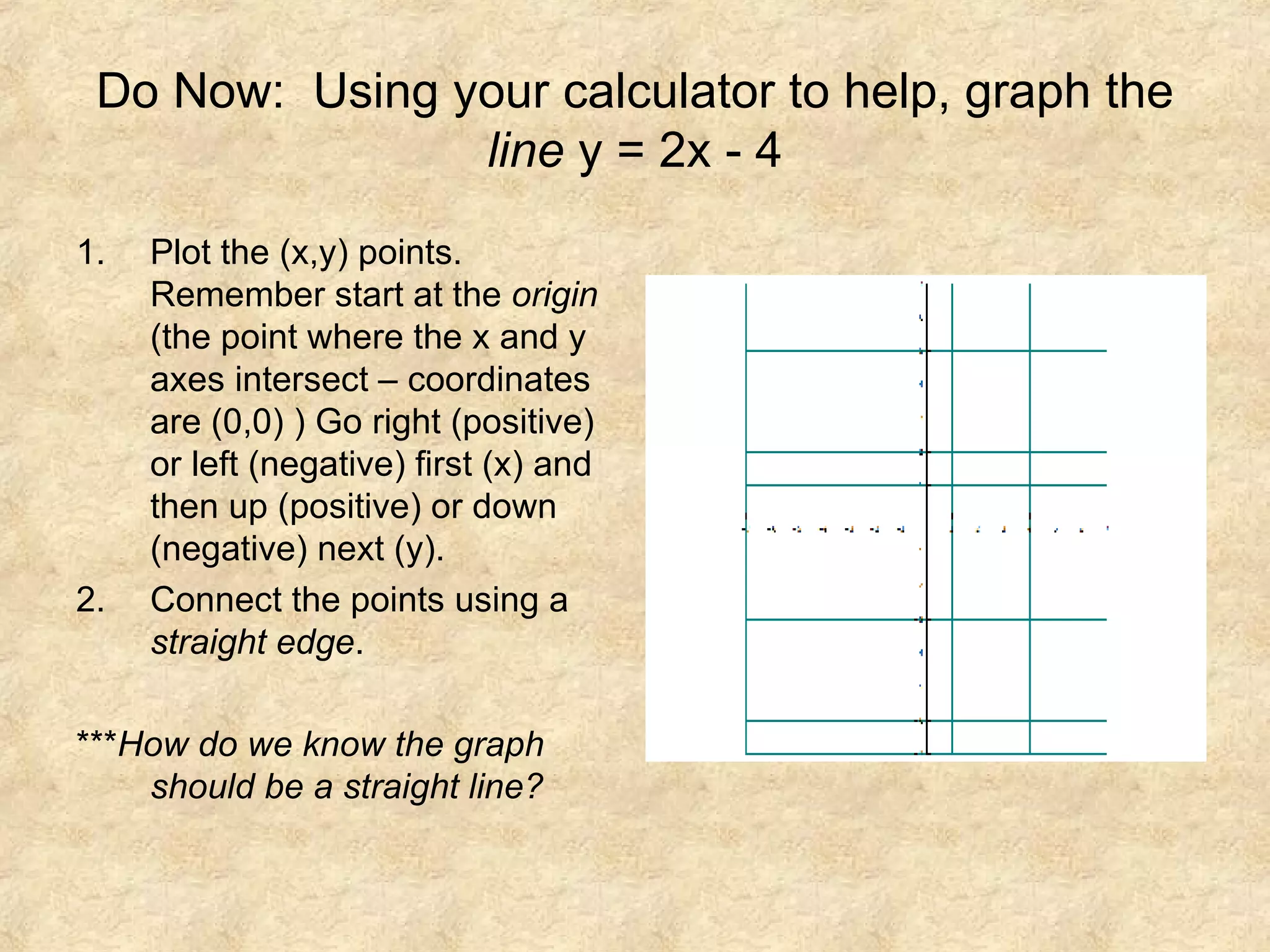
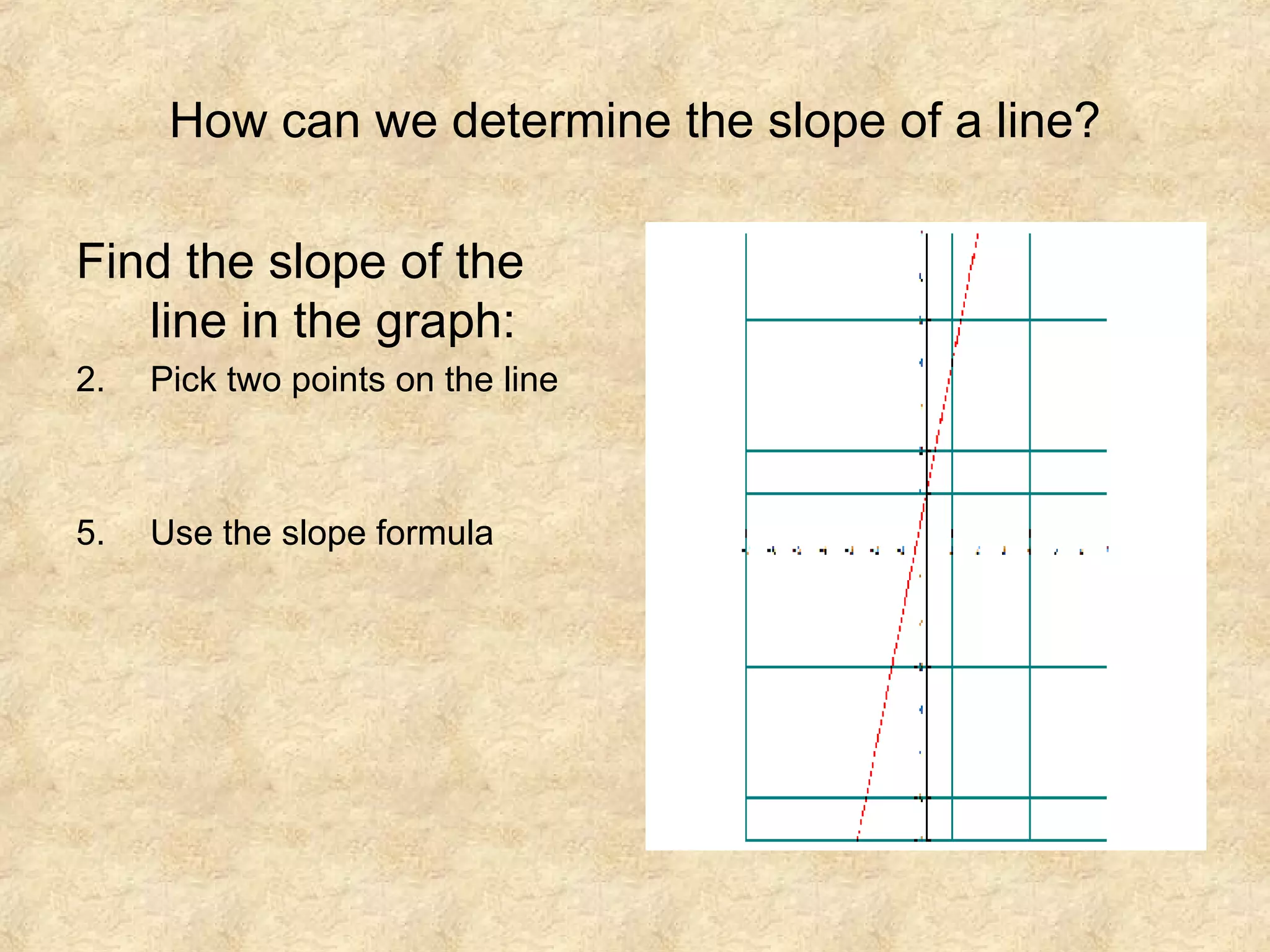
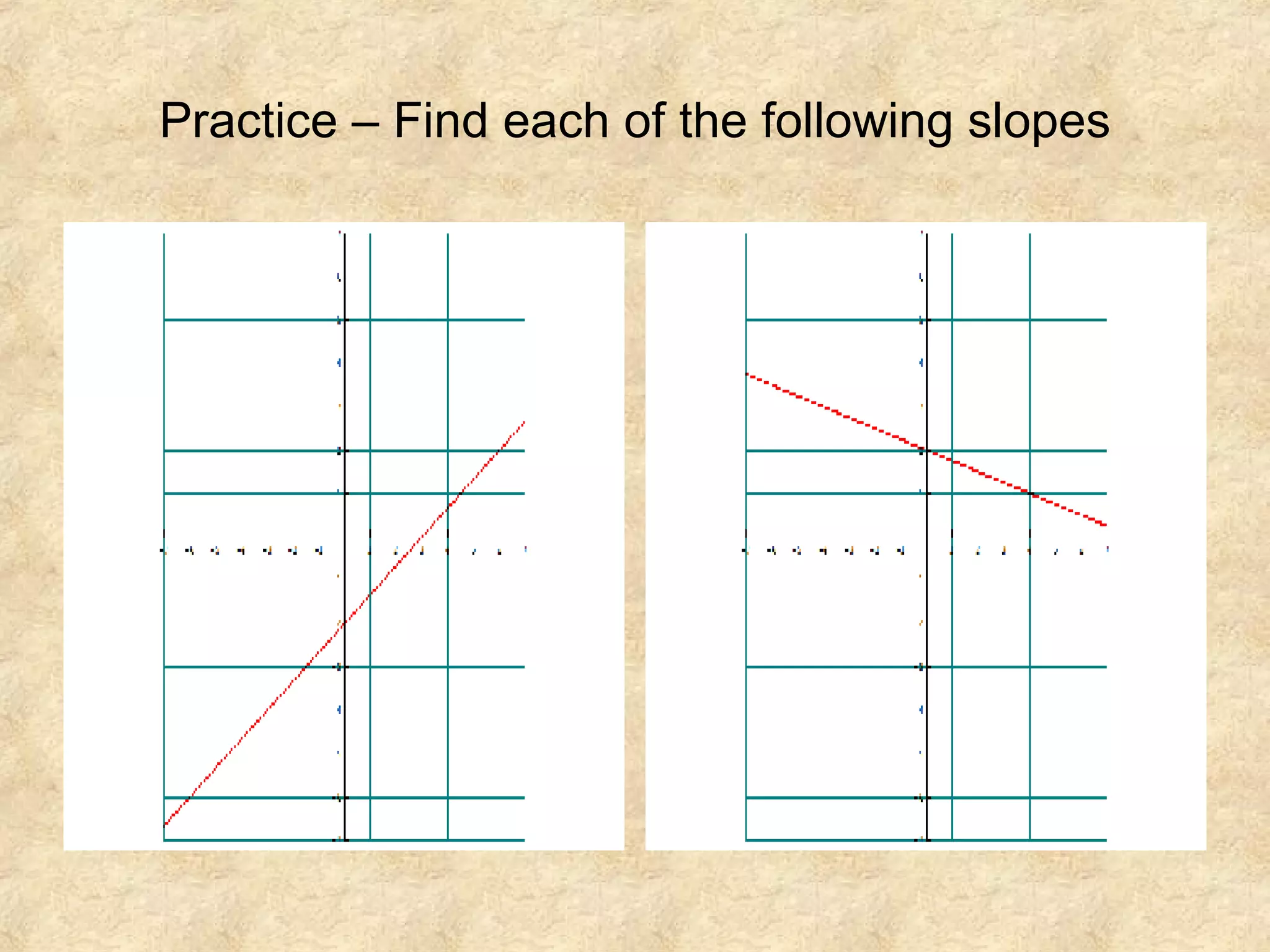
This document discusses graphing linear equations and determining slope. It provides examples of graphing lines with given equations like y = 2x - 4 and finding the slopes between points. Special lines like horizontal and vertical lines are examined, where horizontal lines have a slope of 0 and vertical lines are undefined. Pairs of lines are graphed and observed to have the same or opposite slopes based on their equations. In conclusion, the slope is important in graphing linear equations and representing the steepness of inclined lines.

1. Graphing Linear Equations: Slopes

2. Do Now: Using your calculator to help, graph the line y = 2x - 4 1. Copy the table from the calculator

3. Do Now: Using your calculator to help, graph the line y = 2x - 4 Plot the (x,y) points. Remember start at the origin (the point where the x and y axes intersect – coordinates are (0,0) ) Go right (positive) or left (negative) first (x) and then up (positive) or down (negative) next (y). Connect the points using a straight edge . *** How do we know the graph should be a straight line?

4. Graph y = - 3x + 2 Graph y = ½ x - 4

5. What do the numbers in the equations represent? y = mx + b Where m = the slope of the line b = the y-intercept

6. How can we determine the slope of a line? Find the slope of the line in the graph: Pick two points on the line Use the slope formula

7. Practice – Find each of the following slopes

8. Practice finding slope with no graph: Find the slope of the line passing through (2,1) and (-3,-1) Find the slope of the line passing through (-2,3) and (-4, 0)

9. Special Lines: Find the slope of each of the following Conclusion: Conclusion:

10. Special Lines: Horizontal Lines: Slope is Equation is Vertical Lines: Slope is: Equation is:

11. Graph each of the following pairs of lines. What do you observe? a. y = 2x + 3 What do these lines have in common? b. y = 2x – 1 a. y = - 3x – 2 What do these lines have in common? b. y = - 3x + 3 a. y = ½ x – 3 What do these lines have in common? b. y = ½ x + 5 CONCLUSION: