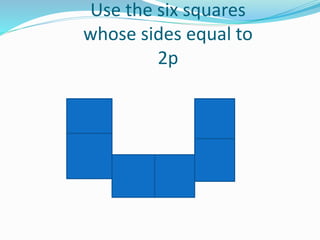
This document discusses graphing parabolas using squares. It explains that parabolas can be graphed by comparing their equations to standard forms and using squares of length 2p, where p is determined by the equation. Examples are given of graphing parabolas from equations x^2=6y and y^2=8x. The focus, vertex, directrix, and latus rectum are identified for each parabola by comparing the equations to the standard forms.

1. Using the method of
squares

2. The parabola we are
to graph are having origin as
our
vertex

3. Compare the equation
to x2=4py
for a parabola with y-axis as its
axis of symmetry

4. Compare the equation
to y2=4px
for a parabola with x-axis as its
axis of symmetry

5. In graphing parabola
we use squares to asses
our graphing

6. Parts of a parabola
Focus: F(0,p)
for a parabola of the form
x2=4py

7. Use the six squares
whose sides equal to
2p

8. Sample: x2=6y
Solution: compare the problem , x2 =6y
to x2 = 4py
4py=6y by transitive property, and
p=1.5 by dividing
4y to both sides

9. From the results
Focus (0, 1.5) or (0,p)
Length of latus rectum 4p or 6 units
Vertex (0,0)
Directrix: y= -1.5 or y= -p

10. We draw the graph
using six squares
with sides equal to 2p or 3 units

11. x2 =6y length of latus rectum
6
1
2 5
4
3 Vertex (0,0)
Directrix: y= -1.5

12. The ordered pairs
 The red colors on previous slide are the points on the
parabola.
 The ordered pairs are found on the vertex of the
squares, upper vertex of squares 1,3,4 and 6.
 The lower portion which is the origin is found on the
sides of squares 3 and 4.


13. Sample 2: y2 =8x
In this case the graph has an
axis of symmetry which is the
x- axis , and the directrix is at
the left side of the origin

14. Solution
y2= 8x will be compared to
 y2=4px, which yields p=2

15. The squares
Length of latus rectum
directrix
Vertex (0,0)
The red colored are the points
on the parabola that passes the
edges of the squares
All the
squares have
the sides of 4
units

16. Thank you for viewing

17. Virgilio Rollon Paragele
Tomas Cabili National High
School