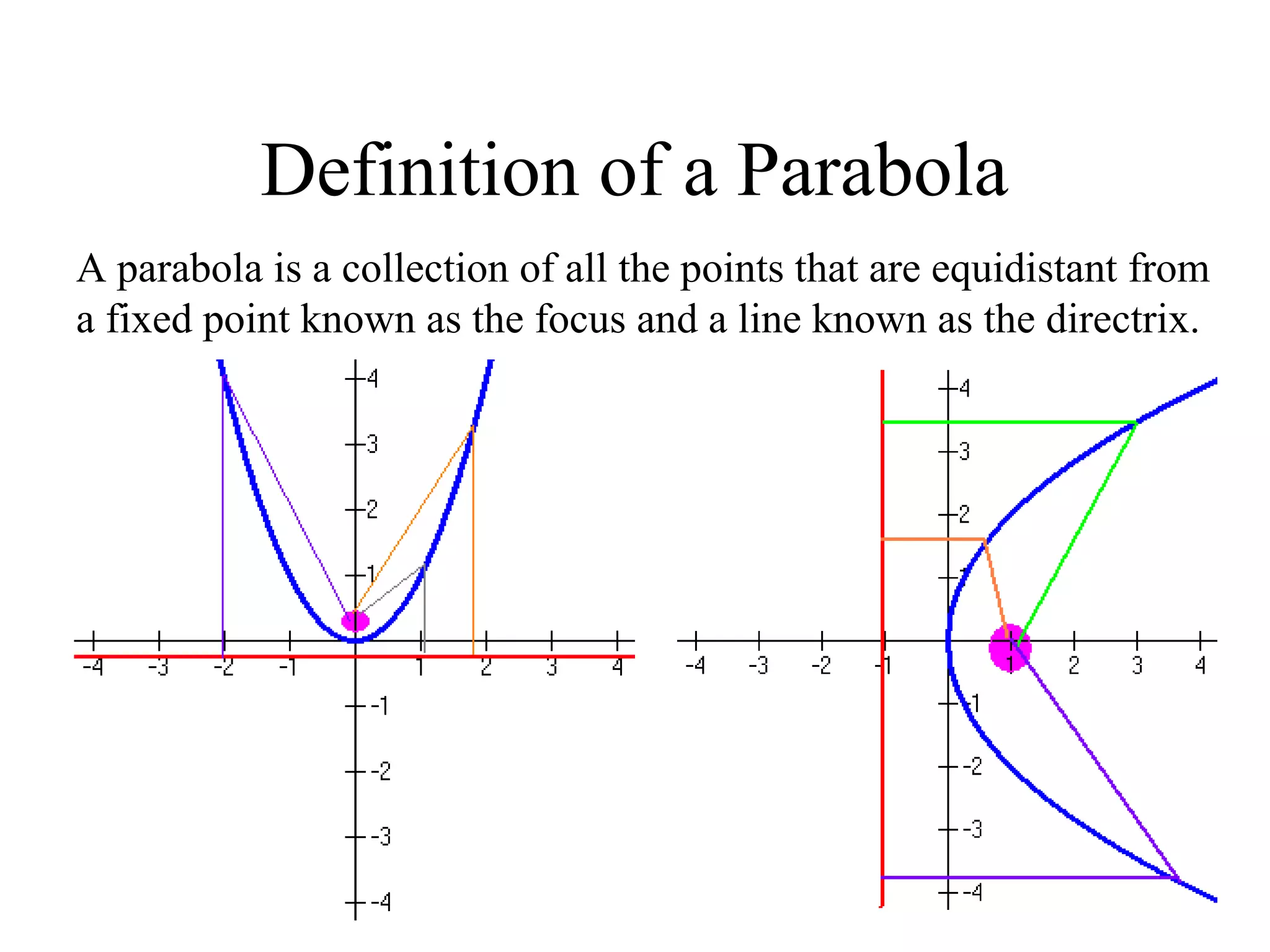
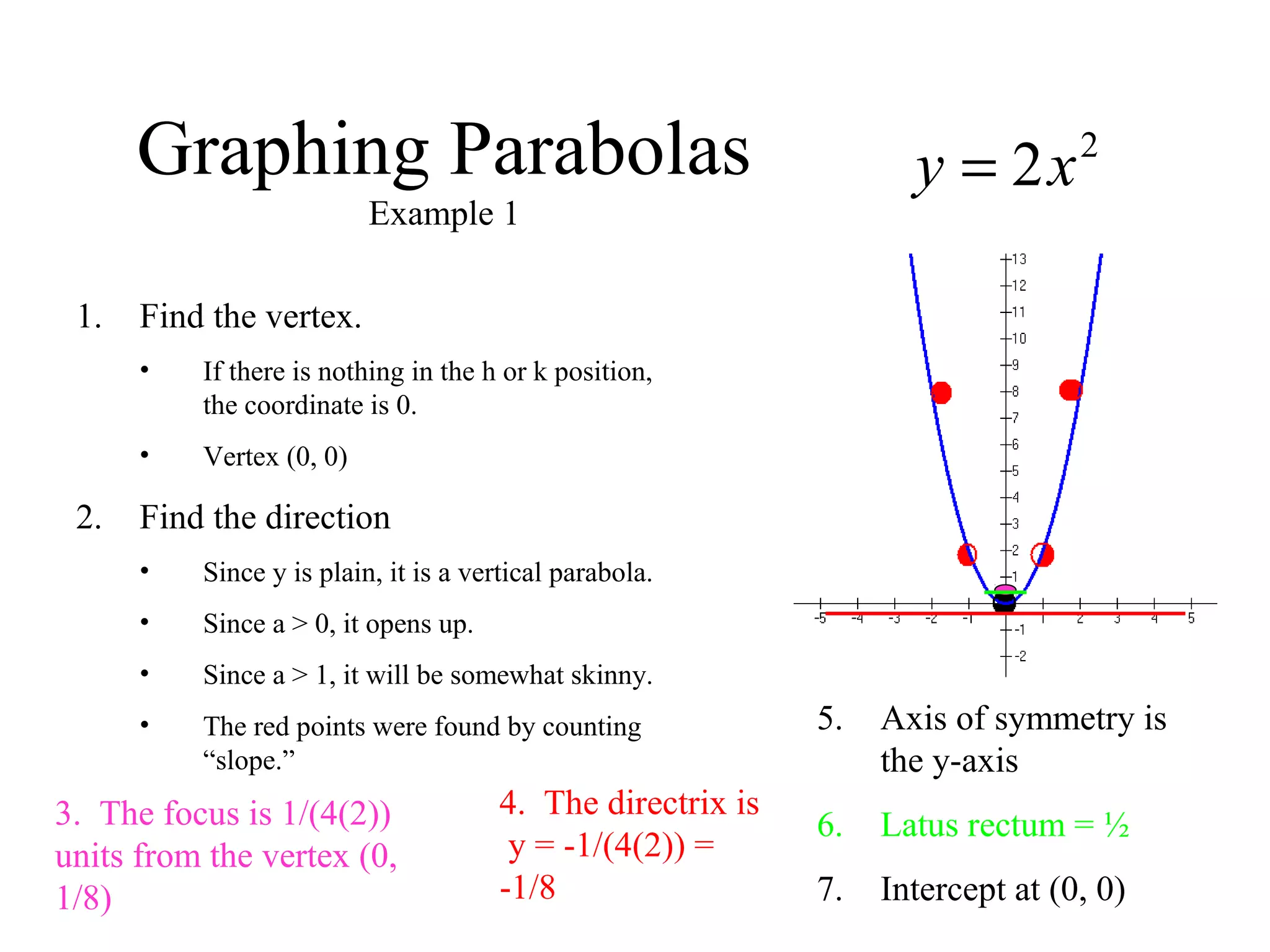
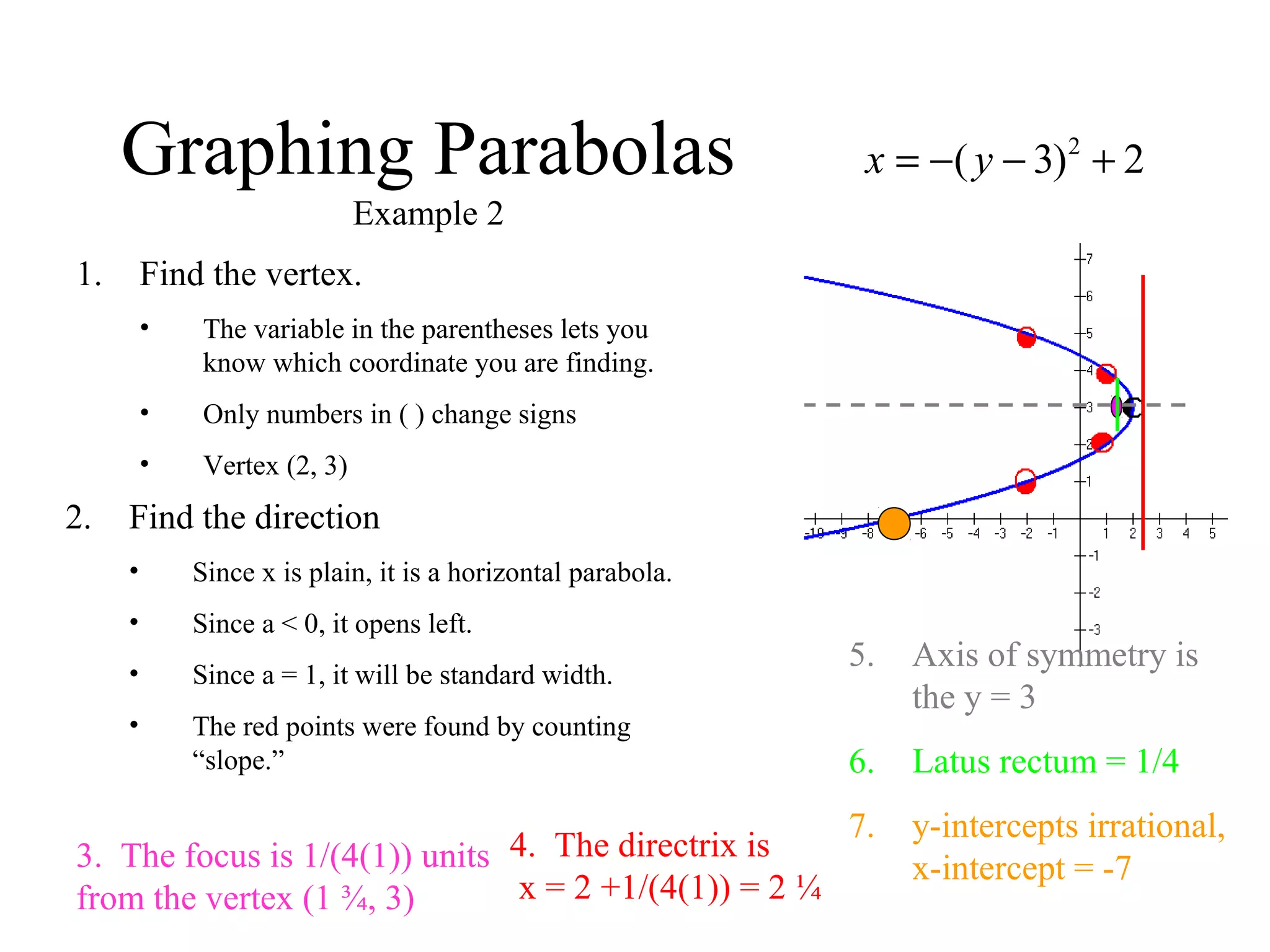
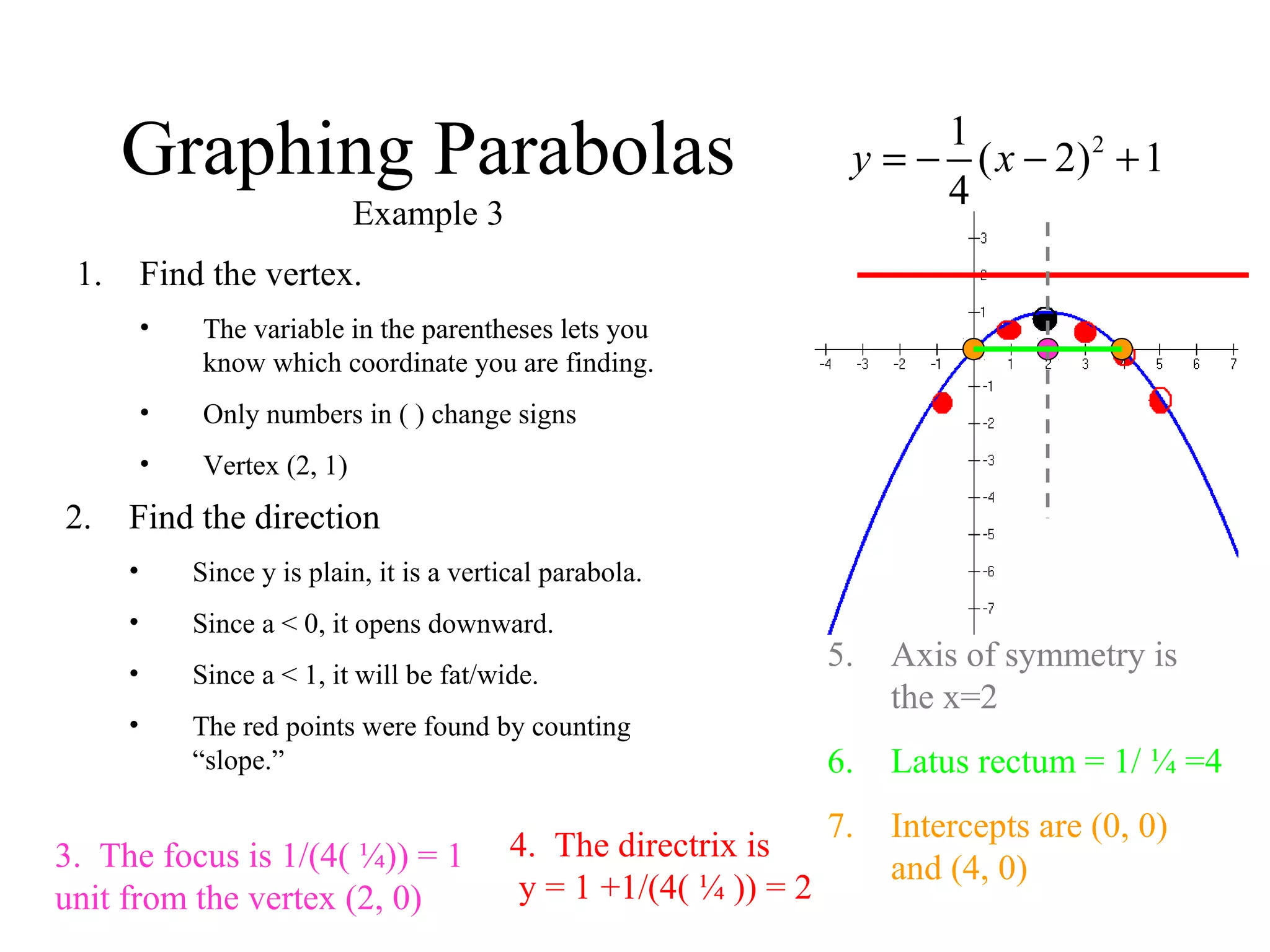
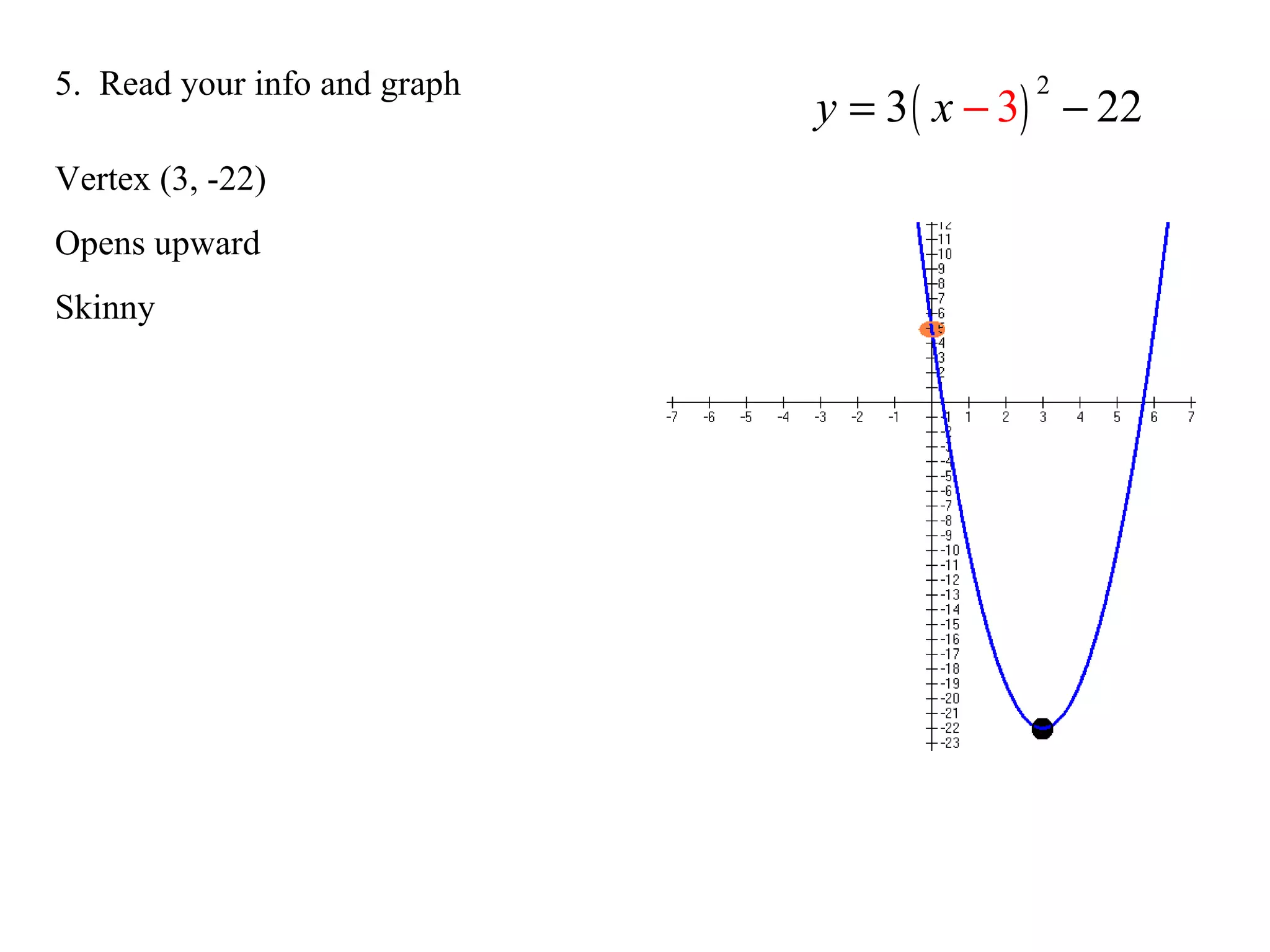
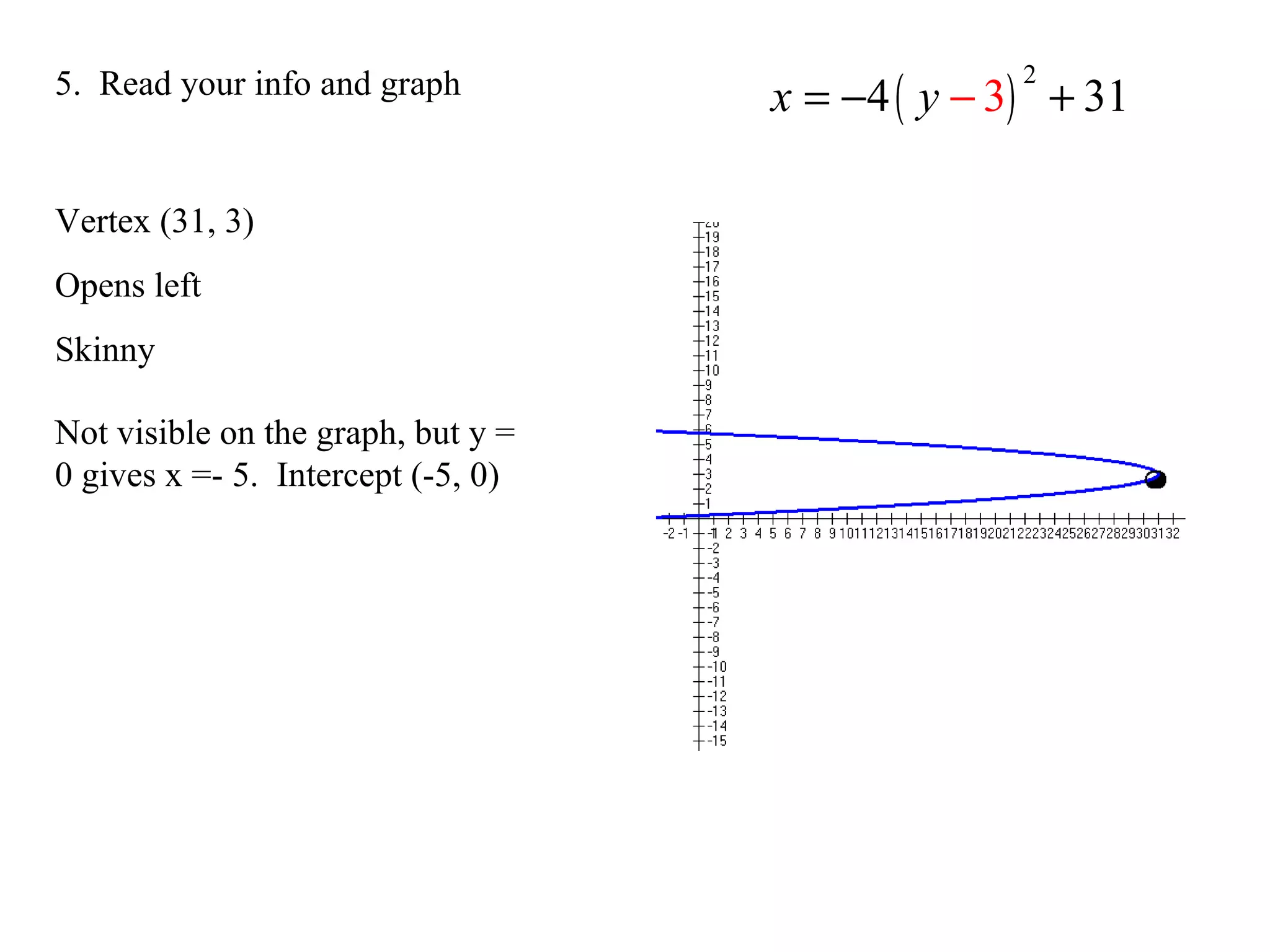
The document provides an overview of parabolas, including their definition, parts, and equations in both vertical and horizontal forms. It outlines steps for graphing parabolas, identifying vertices, focuses, directrices, axes of symmetry, and latus rectums, while also including examples and methods for completing the square. The content is designed to help students apply algebraic concepts to graph parabolas effectively.

1. Parabolas
Algebra II, Sections 11.1 and 11.5
State Standards: Algebra II, Standards 16.0 and 17.0
Mathematical Analysis, Standard 5.1

2. Definition of a Parabola
A parabola is a collection of all the points that are equidistant from
a fixed point known as the focus and a line known as the directrix.

3. Parts of a Parabola
The parabola
The Focus
1/4a units from the
vertex
The Directrix
1/4a units from the vertex
Latus Rectum
Passes through the focus
1/a units long
Axis of
Symmetry

4. Recognizing a Parabola: General Form
2
2
0
0
Ax Ex Dy F or
Cy Ex Dy F
+ + + =
+ + + =
Either A or C is missing
Standard Forms
2 2
2
2
or Center at (0, 0)
( )
( ) +h Center at (h, k)
y ax x ay
y a x h k or
x a y k
= =
= − +
= −
The focus and directix are located
1/(4a) units from the vertex in the
direction of the plain (unsquared)
variable..
Tip:
y = parabolas open in the y direction. Everything
happens to y.
x = parabolas open in the x direction. Everything
happens to x
Note the positions of h and
k. h goes with x and k goes
with y

5. List of Formulas
Form of Equation
Vertical Horizontal
2
( )y a x h k= − +
Vertex (h, k)
Focus 1
,
4
h k
a
 
+ ÷
 
Directrix
1
4
y k
a
= −
Length of Latus Rectum 1
a
Axis of Symmetry x = h
0
0
a
a
>
<
U
I
Direction
2
( )x a y k h= − +
(h, k)
1
,
4
h k
a
 
+ ÷
 
1
4
x h
a
= −
1
a
y = k
0
0
a
a
> ⊂
< ⊃
p = 1/(4a)

6. Graphing Parabolas
Acceptable
• Find the vertex
• Find the direction
• Make some
acknowledgement of a
and the width of the
parabola. (i.e. wide or
narrow)
Exemplary
• Find the vertex
• Find the direction
• Use a to roughly count the
“slope” of the parabola.
• Able to find (when asked)
– Focus
– Directrix
– Axis of symmetry
– Size of latus rectum
• Finds intercepts when
practicable.

7. Graphing Parabolas
Example 1
2
2y x=
1. Find the vertex.
• If there is nothing in the h or k position,
the coordinate is 0.
• Vertex (0, 0)
2. Find the direction
• Since y is plain, it is a vertical parabola.
• Since a > 0, it opens up.
• Since a > 1, it will be somewhat skinny.
• The red points were found by counting
“slope.”
3. The focus is 1/(4(2))
units from the vertex (0,
1/8)
4. The directrix is
y = -1/(4(2)) =
-1/8
5. Axis of symmetry is
the y-axis
6. Latus rectum = ½
7. Intercept at (0, 0)

8. Graphing Parabolas
Example 2
2
( 3) 2x y= − − +
1. Find the vertex.
• The variable in the parentheses lets you
know which coordinate you are finding.
• Only numbers in ( ) change signs
• Vertex (2, 3)
2. Find the direction
• Since x is plain, it is a horizontal parabola.
• Since a < 0, it opens left.
• Since a = 1, it will be standard width.
• The red points were found by counting
“slope.”
3. The focus is 1/(4(1)) units
from the vertex (1 ¾, 3)
4. The directrix is
x = 2 +1/(4(1)) = 2 ¼
5. Axis of symmetry is
the y = 3
6. Latus rectum = 1/4
7. y-intercepts irrational,
x-intercept = -7

9. Graphing Parabolas
Example 3
21
( 2) 1
4
y x= − − +
1. Find the vertex.
• The variable in the parentheses lets you
know which coordinate you are finding.
• Only numbers in ( ) change signs
• Vertex (2, 1)
2. Find the direction
• Since y is plain, it is a vertical parabola.
• Since a < 0, it opens downward.
• Since a < 1, it will be fat/wide.
• The red points were found by counting
“slope.”
3. The focus is 1/(4( ¼)) = 1
unit from the vertex (2, 0)
4. The directrix is
y = 1 +1/(4( ¼ )) = 2
5. Axis of symmetry is
the x=2
6. Latus rectum = 1/ ¼ =4
7. Intercepts are (0, 0)
and (4, 0)

10. Completing the Square on a Parabola
1. Move the “plain”variable to one side and everything else to the
other. Divide by the coefficient of this variable if needed.
2. Group the variables.
3. Factor out the “squared” coefficient.
4. Complete the square
a) Write down the x (or y) coefficient
b) Divide it by 2 (or multiply by ½)
c) Square and add the result inside the parentheses. Subtract what you really added
on the end
d) Factor as a perfect square trinomial (it’s the middle number)
5. Read your information.
We want to turn this
2
2
0
0
Ax Ex Dy F or
Cy Ex Dy F
+ + + =
+ + + =
into
2
2
( )
( ) +h
y a x h k or
x a y k
= − +
= −

11. Example 1
2
3 18 5 0x x y− − + =
1. Move the plain variable (y) to one
side and everything else to the other
2
3 18 5y x x= − +
2. Group the variables ( )2
3 18 5y x x= − +
3. Factor out the squared coefficient ( )2
3 6 5y x x= − +
4. Complete the square
Write down the coefficient -6
Divide it by 2 -3
Square and add inside the ( ) 9
Subtract what you truly added
on the back 3(9)
Factor as a perfect square trinomial
(middle number)
( )2
3 6 5 3(9)9y x x + −= − +
( )
2
33 22y x −= −

12. 5. Read your info and graph
( )
2
33 22y x −= −
Vertex (3, -22)
Opens upward
Skinny

13. Example 2
2
8 2 48 10 0y x y− − + − =
1. Move the plain variable (x) to one
side and everything else to the other.
Divide by the x coefficient.
2
2
2 8 48 10
4 24 5
x y y
x y y
= − + −
= − + −
2. Group the variables
( )2
4 24 5x y y= − + −
3. Factor out the squared coefficient ( )2
4 6 5x y y= − − −
4. Complete the square
Write down the coefficient -6
Divide it by 2 -3
Square and add inside the ( ) 9
Subtract what you truly added
on the back -4(9)
Factor as a perfect square trinomial
(middle number)
( )2
4(4 6 959 )x y y + += − − −
( )
2
4 313x y −= − +

14. ( )
2
4 313x y −= − +5. Read your info and graph
Vertex (31, 3)
Opens left
Skinny
Not visible on the graph, but y =
0 gives x =- 5. Intercept (-5, 0)