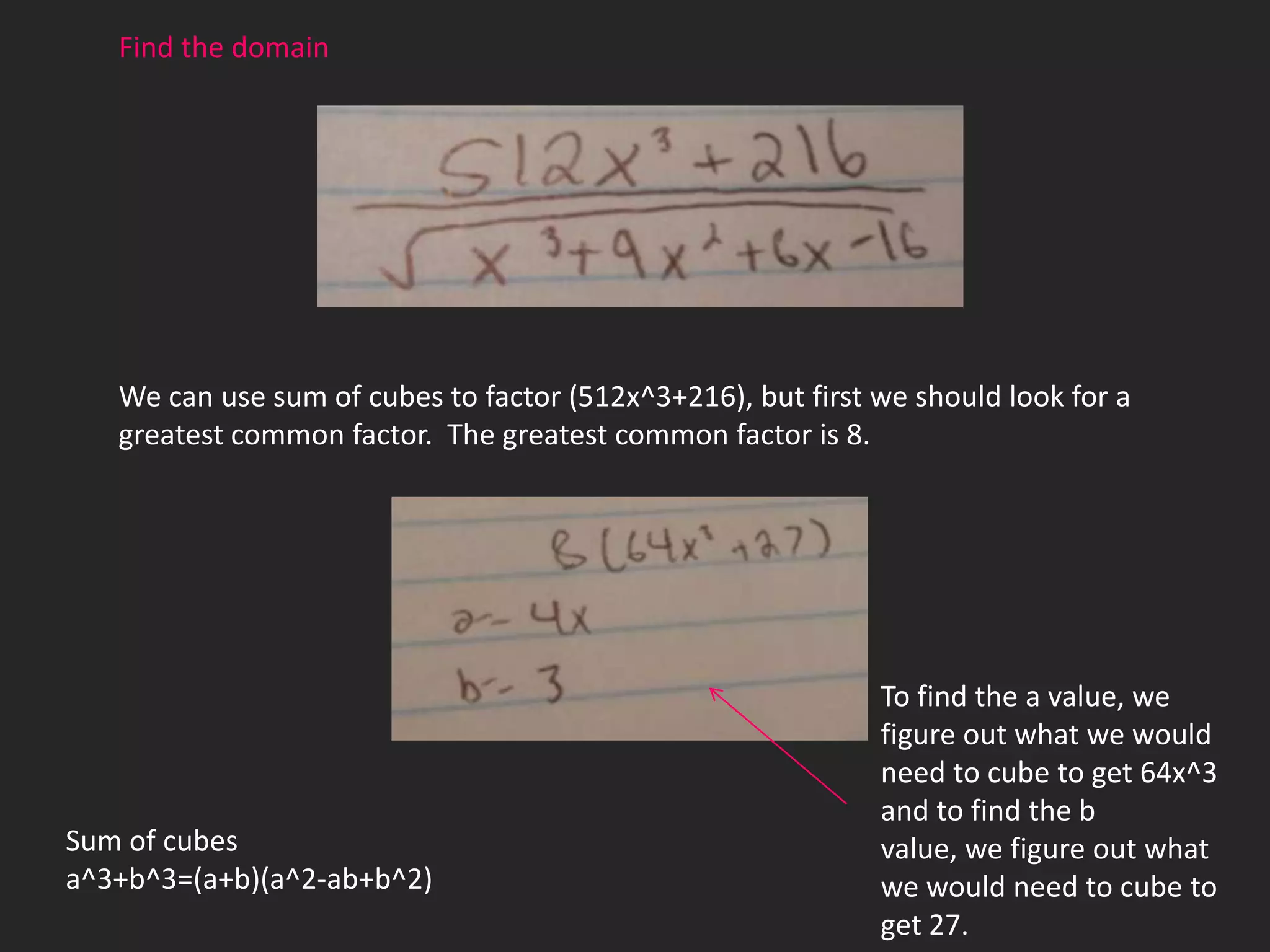
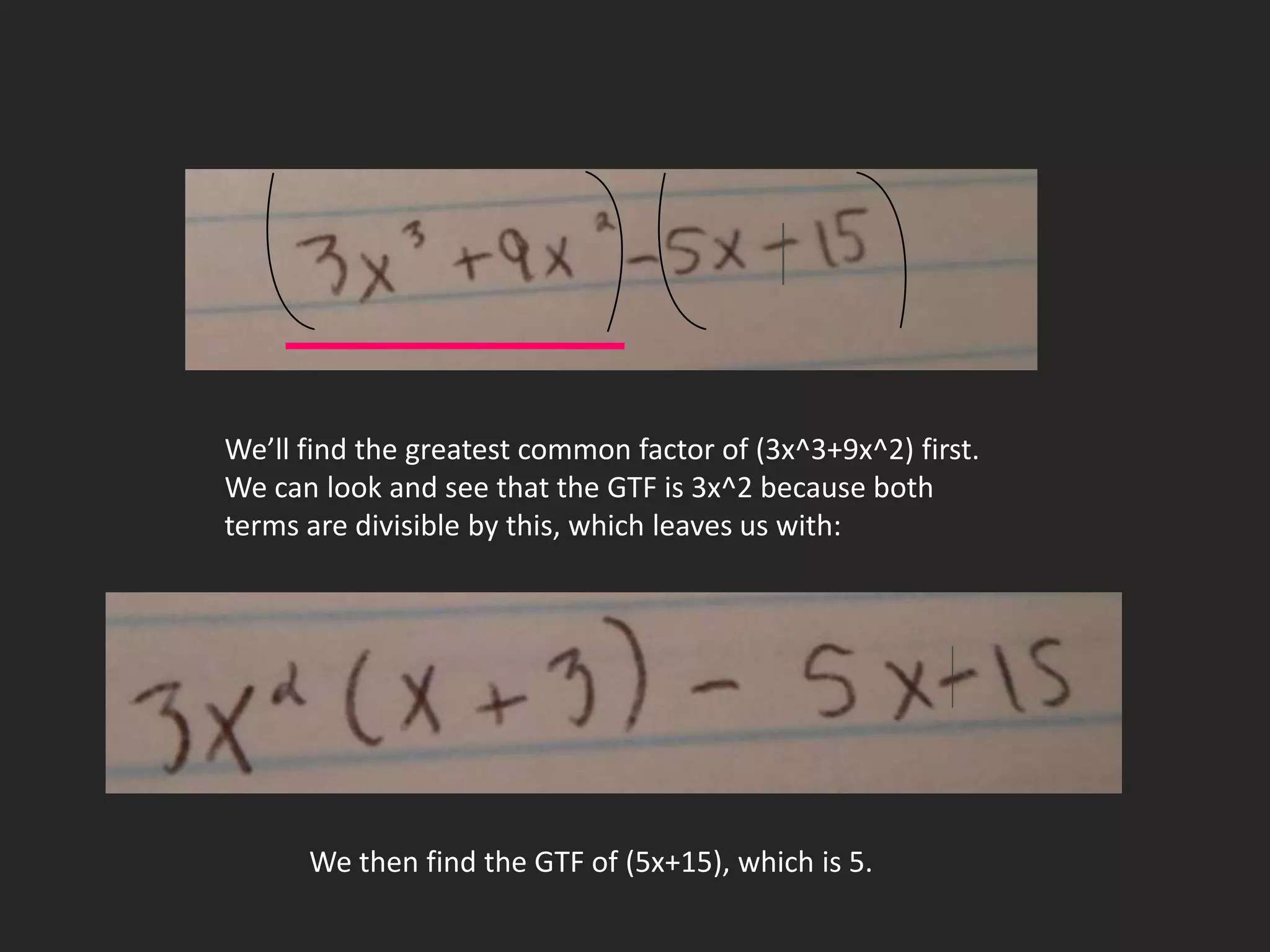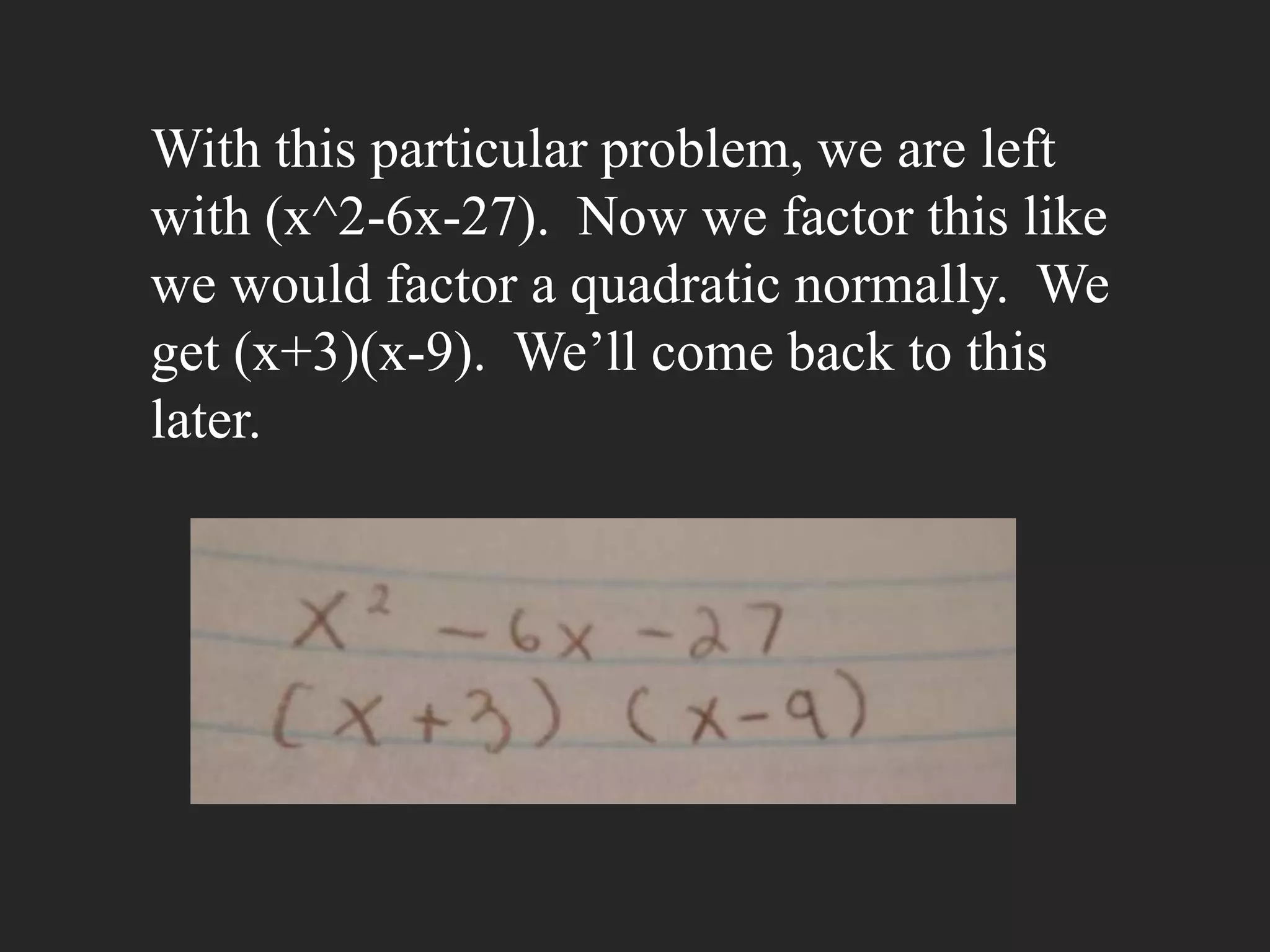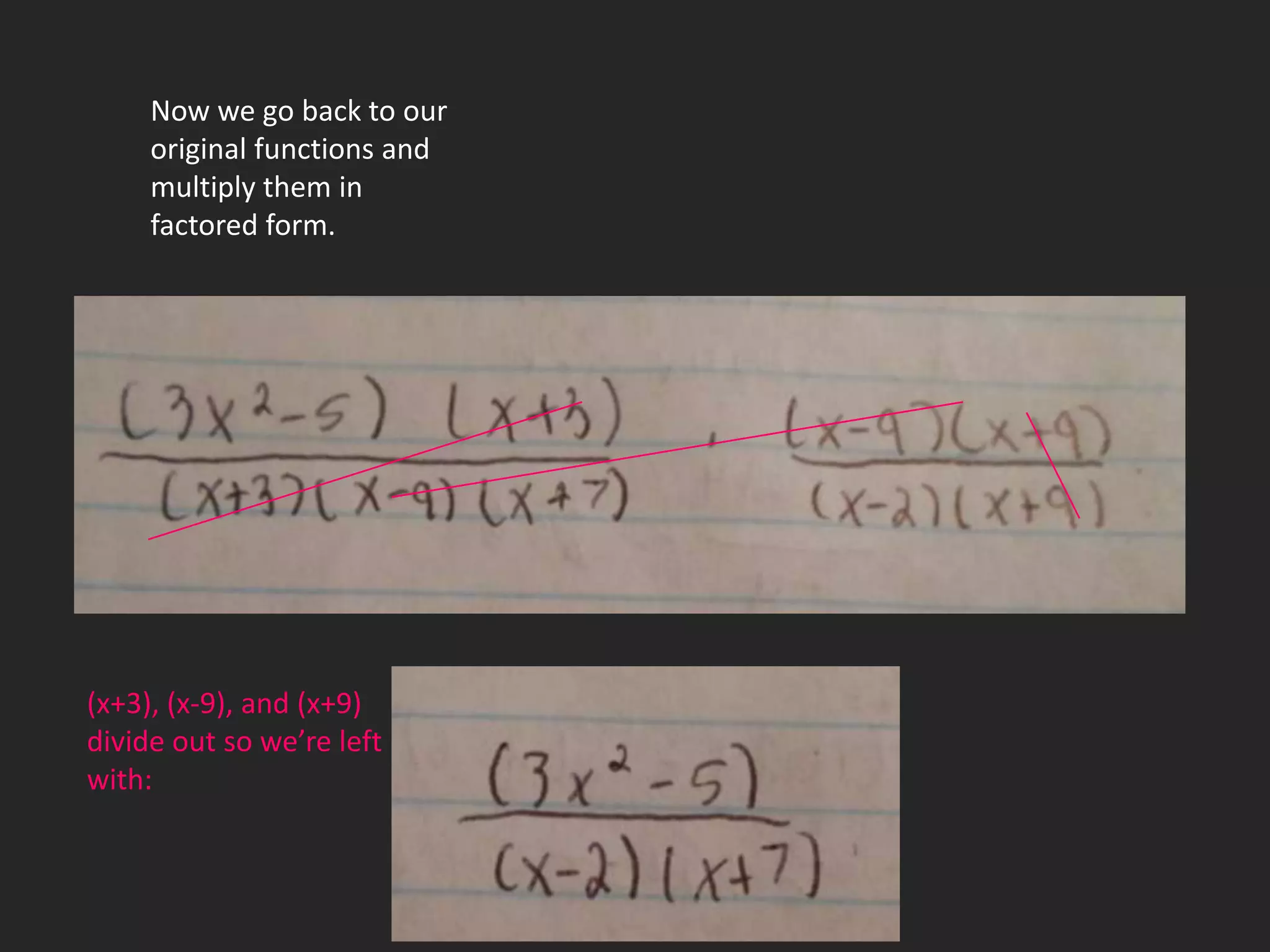This document is a journey through pre-calculus functions told through photographs, math problems, and poetry. It discusses the challenges of learning difficult math concepts and emphasizes overcoming obstacles through perseverance. It uses examples like factoring polynomials and finding the domain of rational functions to illustrate key concepts. Poetry reflects on feeling overwhelmed but realizing the value of learning from mistakes to achieve success.