D.e.v

D.E.V Project

By Afsheen, Colleen, and Meg

Caution: Music plays throughout

Avengers Assemble! (The Problems)
• Captain America
• Iron Man
• Thor
• The Hulk
• Black Widow
• Hawkeye

Captain America
Captain America’s shield has a radius of 12
inches. Find the area of the shield. Then
express the area as a function of the
circumference “C”.

Step 1

Step 1

Find the area of the shield using the formula
A=πr².
A=π12² A=452.39 in²

Step 2

Step 2
Express A as a function of C. The formula for
circumference is C=2πr and the formula for radius
is r=C/2π.
1. r=C/2π 12=C/2π
2. A=πr² 452.39= π12²
3. C=2πr
Make sure you list your three equations with and
without variables.
Step 3

Step 3
• Because we are expressing A as a Function of
C, A must be our solution. So, A=πr².
• Replace “r” with the radius equation.
A=π(C/2π)²
• Simplify the equation. A=C ²/4 π
• Replace the variables with the corresponding
number. 452.39=C ²/4 π

Iron Man
Iron Man is making his Arch Reactor to keep the
shrapnel away from his heart, but he needs to
find the solutions to

5x²+10x-4=7

Step 1

Step 1
Bring the “4” to the other side. (Add “4” to each
side).

5x²+10x-4=7
+4 +4

5x²+10x=11
Step 2

Step 2
Factor out the “5.”

5x²+10x=11

5(x²+2x)=11

Step 3

Step 3
Create a new “c” value by using the formula (b/2)²

“b” value=2
=(2/2)²
=1

5(x²+2x)=11

5(x²+2x__)=11

5(x²+2x+1)=11
Step 4

Step 4
Because a new “c” value was created, and added to one side. It must
be added to the other. (Don’t forget about the 5 that has been
divided out!!!)

1x5=5  Add 5 to 11 on the other side.

(What you do to one side, must be done to the other.)

5(x²+2x+1)=11

5(x²+2x+1)=11+5
Step 5

Step 5
To factor the rest, take the “b” value and divide it by 2.

2/2=1

Take out the “c” value and square your new equation.
Replace “b” with the new “b” you found.
5(x²+2x+1)=16

5(x+1)²=16
Step 6

Step 6
Get “x” by itself.
Divide by 5:
5(x+1)²=16
5 5
Square Root:
√(x+1)²= √(16/5)
x+1= √(16/5)
(Notice that 16 has a square root)

Subtract 1 from each side:
x+1=4/√5
-1 -1
x= -1(4/± √5)

The Hulk
The Hulk just smashed a wall that is worth
(3x+30) ´

How many small wall pieces are there now?

Step 1

Step 1
You need to expand the quantity to find how
many pieces there are.

(3x+30)´

(3x+30)(3x+30)(3x+30)(3x+30)

Step 2

Step 2
Then factor by F.O.I.L. (First. Outside. Inside. Last)
But, you can only F.O.I.L. 2 quantities at a time.

(3x+30)´

(9x²+90x+90x+900)(9x²+90x+90x+900)
Step 3

Step 3
Combine “like terms.”

(9x²+90x+90x+900)(9x²+90x+90x+900)

(9x²+180x+900)(9x²+180x+900)
Step 4

Step 4
Now, you have 2 quantities again. Factor these out.

(9x²+180x+900)(9x²+180x+900)

81x´+1620x³+8100x²+1620x³+32400x²+162000x+8100x²+162000x+810000
Step 5

Step 5
Remember to combine “like terms.”

81x´+1620x³+8100x²+1620x³+32400x²+162000x+8100x²+162000x+810000

81x´+3240x³+48600x²+324000x+810000

Hawkeye
Hawkeye shoots an arrow and draws the
parabola it makes on a graph. The parabola
has a vertex at (5,6) and is passing through the
point (9,3). Find the equation for this
quadratic that satisfies the given conditions.

Step 1

Step 1
Draw a graph of the given information.

6

3
.
0
5 9

Step 2

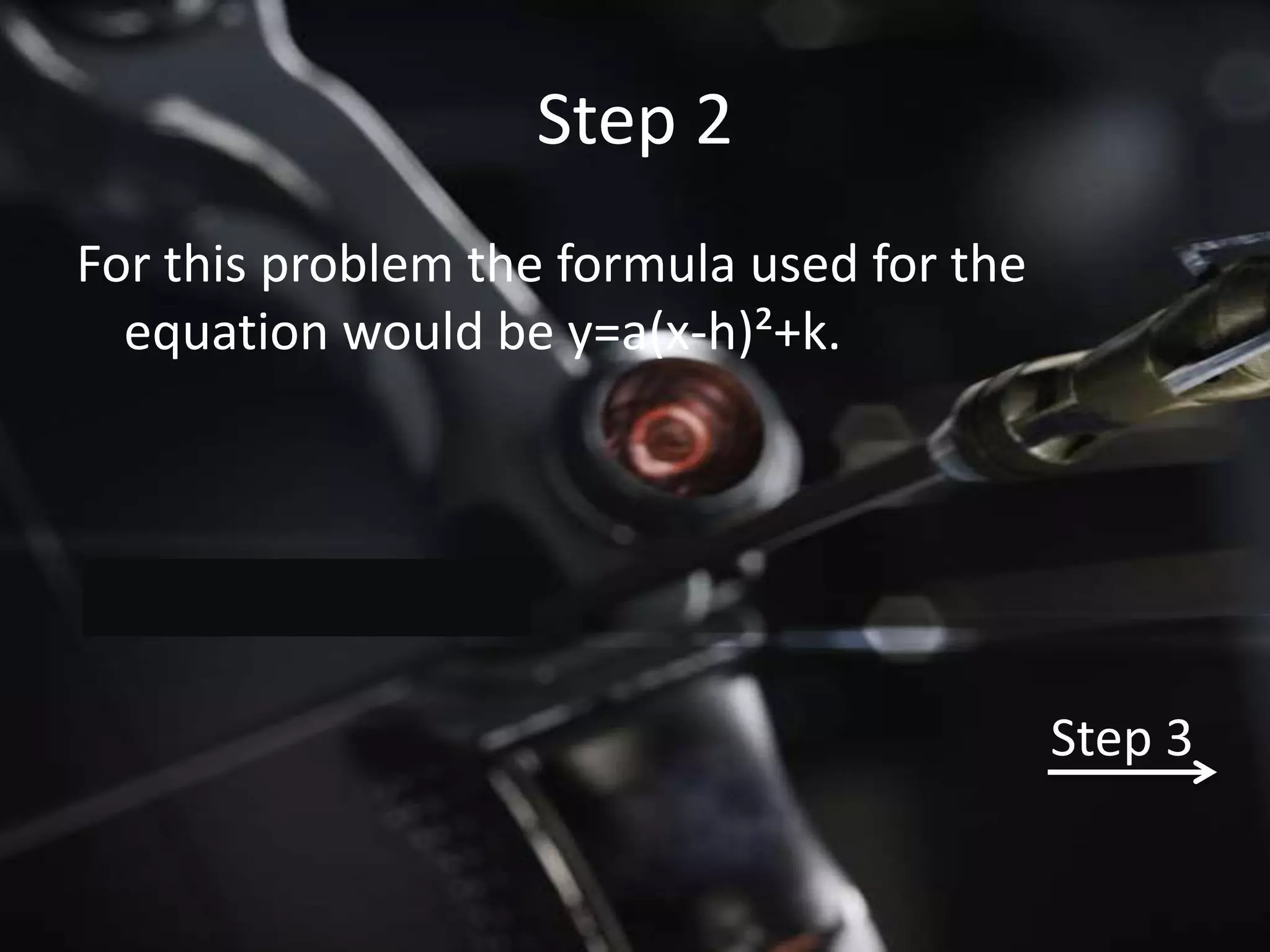
Step 2
For this problem the formula used for the
equation would be y=a(x-h)²+k.

Step 3

Step 3
Now match the variables with the correct
numbers. “a” will not have a number because
we are trying to solve for “a”.
We were told that the parabola has a vertex at
(5,6) and passes through point (9,3).

h=5 k=6 x=9 y=3
Step 4

Step 4
Replace the variables in the equation with the
corresponding numbers.
h=5 k=6 x=9 y=3
3=a(9-5)²+6

Step 5

Step 5
Solve for “a”.
3=a(9-5)²+6 Find 9-5 and square the difference
3=16a+6 Subtract 6 from each side
-6 -6
-3=16a Divide both sides by 16
16 16
-3/16=a
Step 6

Step 6
Put -3/16 into the equation 3=a(9-5)²+6 in
replacement of “a.”
3=-3/16(9-5) ²+6

Step 7

Step 7
Replace 3 with “y” and replace 9 with “x.”

Finished equation:
y=-3/16(x-5)²+6

Thor

Thor throws his hammer across the surface of a body of water and it cause it to skip
like a stone. Thor calculated that the function for its skip was:

f(x)=(x+7)(x+4)(x+1)²(x-2)(x-5)

Now Thor wants to know the domain of this function and what the graph would look
like.

Step 1

Take all of the X’s and separate them such as (x+7) and (x-2) and then set them all
equal to zero to find all of the zeros.

X+7=0 X+4=0 (X+1)²=0 X-2=0 X-5=0
-7 -7 -4 -4 √(X+1)²= √0 +2+2 +5+5
X = -7 X = -4 X+1 =0 X=2 X=5
-1 -1
X = -1

Step 2
Sketch out a graph and mark all of the zeros on the x-axis.

-7 -4 -1 2 5

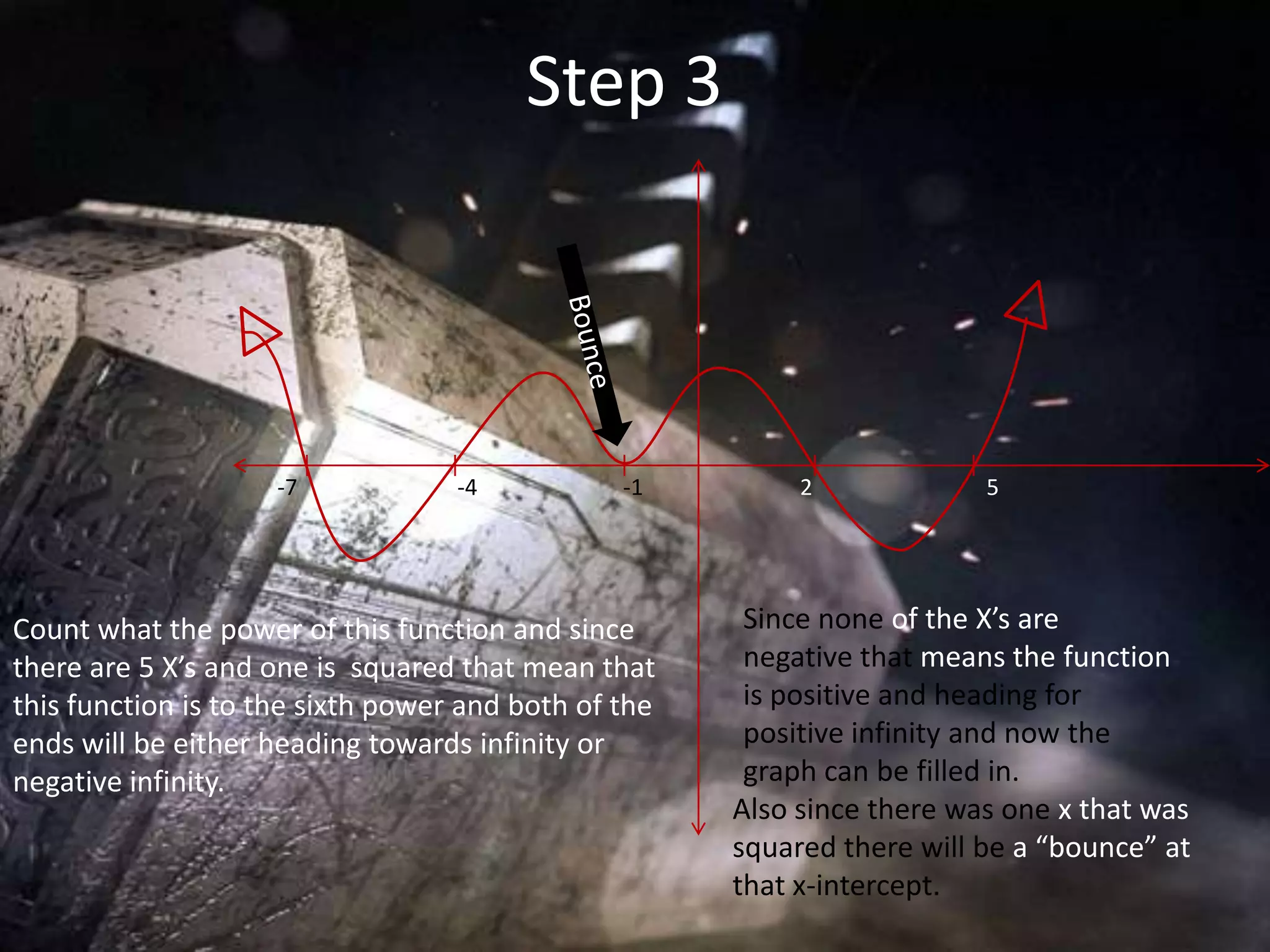
Step 3

-7 -4 -1 2 5

Count what the power of this function and since Since none of the X’s are
there are 5 X’s and one is squared that mean that negative that means the function
this function is to the sixth power and both of the is positive and heading for
ends will be either heading towards infinity or positive infinity and now the
negative infinity. graph can be filled in.
Also since there was one x that was
squared there will be a “bounce” at
that x-intercept.

Step 4

To find the domain you need to look where the function is positive and everything
that is positive is part of the domain.
Looking at this function it is clear to see that
it is positive from negative infinity to negative
seven and then from negative four to positive
two and then from five to infinity. With all of
this information the domain can be found -7 -4 -1 2 5
and would look like this:

D: (- ∞, -7]U[-4, 2]U[5, ∞)

Black Widow

Suppose Black Widow had a radical function
that was:
√ x²+5x-36
She wants to know the X’s, domain, and range.

Step 1

The first step is to set it greater than or equal to zero.

√x²+5x-36 ≥ 0

Step 2

The second step is to take the square root of both sides.
(√x²+5x-36 )² ≥ 0² = x²+5x-36 ≥ 0

Step 3
The third step is to factor it.

x²+5x-36 ≥ 0 (x+9)(x-4) ≥ 0

This means the X’s are:

X= -9 X=4

Leaving the domain and range to be:

D: (- ∞, -9]U[4, ∞)
R: [0, ∞)

D.e.v

More Related Content

What's hot

Viewers also liked

Similar to D.e.v

D.e.v