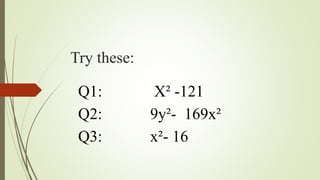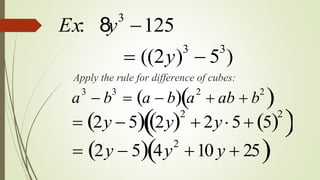This document provides an outline for teaching various factoring techniques. It begins with definitions of algebraic expressions, polynomials, factors, and factoring. It then covers finding the greatest common factor, factoring by using the GCF, factoring by grouping, factoring differences of squares, factoring perfect square trinomials using the special formula, and solving word problems using factoring. Examples are provided for each technique to demonstrate how to factor different polynomial expressions. Special cases like the sum and difference of cubes are also discussed. The document concludes with an explanation of the quadratic formula.

2. Topic:
Factoring Expressions/Techniques
Hafiz M. Arslan
Motor City

3. Outline:
 Some Basic Definitions
 How to find GCF
 Factoring by using GCF
 Factoring by using Grouping
 Factoring Polynomials by using Difference of Squares
 Factoring Trinomials by using Perfect Square
 Factoring Quadratic
 Factoring by using Cube formula
 Solving Quadratic by Quadratic Formula
 Real word problems

4. Algebraic Expressions
An algebraic expression is a mathematical phrase that can
contain ordinary numbers, variables (like x or y) and operators
(like add,subtract,multiply, and divide).
Here are some algebraic expressions:
a + 1
a - b
3x
x - a / b

5. Polynomials
A polynomial is an expression consisting
of variables and coefficients which only employs the
operations of addition, subtraction, multiplication, and
non-negative integer exponents.
An example of a polynomial of a single variable x is
x2 − 4x + 7.
 An example in three variables is x3 + 2xyz2 − yz + 1.

6. Some Basic Definitions
Factors (either numbers or polynomials)
When an integer is written as a product of
integers, each of the integers in the product is a
factor of the original number.
When a polynomial is written as a product of
polynomials, each of the polynomials in the
product is a factor of the original polynomial.

7. Factoring
Factoring a polynomial
means expressing it as a
product of other polynomials.

8. Greatest Common Factor
Greatest common factor – largest quantity that is a factor
of all the integers or polynomials involved.
Finding the GCF of a List of Integers or Terms
1) Prime factor the numbers.
2) Identify common prime factors.
3) Take the product of all common prime factors.
• If there are no common prime factors, GCF is 1.

9. Greatest Common Factor
Find the GCF of each list of numbers.
1) 12 and 8
12 = 2 · 2 · 3
8 = 2 · 2 · 2
So the GCF is 2 · 2 = 4.
2) 7 and 20
7 = 1 · 7
20 = 2 · 2 · 5
There are no common prime factors so the GCF is 1.
Example

10. Greatest Common Factor
1) x3 and x7
x3 = x · x · x
x7 = x · x · x · x · x · x · x
So the GCF is x · x · x = x3
2) 6x5 and 4x3
6x5 = 2 · 3 · x · x · x
4x3 = 2 · 2 · x · x · x
So the GCF is 2 · x · x · x = 2x3
Example

11. Factoring Method #1
Factoring polynomials with a common monomial
factor (using GCF).
**Always look for a GCF before using any other
factoring method.

12. Steps:
Find the greatest common factor (GCF).
Divide the polynomial by the GCF. The
quotient is the other factor.
Express the polynomial as the product
of the quotient and the GCF.

13. Factoring Method #1
3 2 2
: 6 12 3Example c d c d cd 
3GCF cdStep 1:
Step 2: Divide by GCF
(6c3
d 12c2
d2
 3cd)  3cd 
2c2
 4cd  1

14. Factoring Method #1
 3cd(2c2
 4cd  1)
The answer should look like this:
Ex: 6c3
d 12c2
d2
 3cd

15. Factoring Method #1
1. 6x
3
 3x
2
 12x
2. 5x
2
10x  35
3. 16x3
y4
z 8x2
y2
z3
12xy3
z2
Factor these on your own looking for a GCF.

16. Factoring Method #2
Factoring By Grouping
for polynomials
with 4 or more terms

17. Factoring Method #2
Step 1: Group
3 2
3 4 12b b b  
Example 1:
 b
3
 3b
2
  4b 12 
Step 2: Factor out GCF from each group
 b2
b 3  4 b 3 
Step 3: Factor out GCF again  b  3  b
2
 4 

18. Factoring Method #2
3 2
2 16 8 64x x x  
 2 x
3
 8x
2
 4x 32 
 2 x
3
 8x
2
  4x  32  
 2 x
2
x  8  4 x  8  
Example 2:

19. Factoring Method #2
 2 x 8  x
2
 4  
 2 x 8  x  2  x  2  

20. Factor 90 + 15y2 – 18x – 3xy2.
90 + 15y2 – 18x – 3xy2
= 3(30 + 5y2 – 6x – xy2)
= 3(5 · 6 + 5 · y2 – 6 · x – x · y2)
= 3(5(6 + y2) – x (6 + y2)) =
= 3(6 + y2)(5 – x)
Factoring Method #2

21. Factoring Method #3
Factoring polynomials that are a
difference of squares.

22. To factor, express each term as a square of a
monomial then apply the rule...
a2
 b2
 (a  b)(a  b)
Factoring Method #3

23. Ex: x2
16 
x2
 42

(x  4)(x  4)
Factoring Method #3

24. Factoring Method #3
Here is another example:
1
49
x
2
81
1
7
x



2
 92

1
7
x  9



1
7
x  9




25. Try these:
Q1: X² -121
Q2: 9y²- 169x²
Q3: x²- 16

26. Q: Solve the Word problems by using factoring.
1. The area of a square is numerically equal to twice its
perimeter. Find the length of aside of the square.
2. The square of a number equals nine times that number.
Find the number.
3. Suppose that four times the square of a number
equals 20 times that number. What is the number?

27. 4. The combined area of two squares is 20 square
centimeters. Each side of one square is twice as long
as a side of the other square. Find the lengths of the
sides of each square.
5. The sum of the areas of two squares is 234 square
inches. Each side of the larger square is five times the
length of aside of the smaller square. Find the length
of a side of each square.

28. Factoring Method #44

29. Factoring Method #4

30. Factoring Method #4
Perfect Square Trinomials can be
factored just like other trinomials (guess
and check), but if you recognize the
perfect squares pattern, follow the
formula!
a2
 2ab  b2
 (a  b)2
a2
 2ab  b2
 (a  b)2

31. Perfect Squares
Ex: x2
 8x 16
2 
x 
2
4 
2
Does the middle
term fit the
pattern, 2ab?
b
4
a
x   8x

32. x2
 8x 16  x  4 
2
Yes, the factors are (a + b)2 :
Perfect Squares

33. Ex: 4x2
12x  9
2x 
2
3 
2
Does the middle
term fit the
pattern, 2ab?
b
3
a
2x  12x
Perfect Squares

34. 4x2
12x  9  2x  3 
2
Yes, the factors are (a - b)2 :
Perfect Squares

35. If the x2 term has no coefficient (other than 1)...
Step 1: List all pairs of
numbers that multiply to
equal the constant, 12.
x2 + 7x + 12
12 = 1 • 12
= 2 • 6
= 3 • 4
Step 2: Choose the pair that
adds up to the middle
coefficient.
12 = 1 • 12
= 2 • 6
= 3 • 4

36. Step 3: Fill those numbers
into the blanks in the
binomials:
( x + )( x + )
x2 + 7x + 12 = ( x + 3)( x + 4)
3 4

37. Factoring Method #4
Factor. x2 + 2x - 24
This time, the constant is negative!
Step 1: List all pairs of
numbers that multiply to equal
the constant, -24. (To get -24,
one number must be positive and
one negative.)
-24 = 1 • -24, -1 • 24
= 2 • -12, -2 • 12
= 3 • -8, -3 • 8
= 4 • -6, - 4 • 6
Step 2: Which pair adds up to 2?
Step 3: Write the binomial
factors.
x2 + 2x - 24 = ( x - 4)( x + 6)

38. Factoring Method #4
Factor. 3x2 + 14x + 8
This time, the x2 term DOES have a coefficient (other than 1)!
Step 2: List all pairs of
numbers that multiply to equal
that product, 24.
24 = 1 • 24
= 2 • 12
= 3 • 8
= 4 • 6
Step 3: Which pair adds up to 14?
Step 1: Multiply 3 • 8 = 24
(the leading coefficient & constant).

39. So then we can write them in the four terms.
3x2 + 12x + 2 x + 8 =( 3x + 2 )( x + 4 )
3x2 + 14x + 8 = (3x + 2)(x + 4)

40. Special Cases
Sum and Difference of Cubes:
a3
 b3
 a  b  a2
 ab  b2
 
a3
 b3
 a  b  a2
 ab  b2
 

41. Special Cases
3
: 64Example x 
 (x3
 43
) Rewrite as cubes
Apply the rule for sum of cubes:
a
3
 b
3
 a  b  a
2
 ab  b
2
 
 (x  4)(x2
 4x 16)
 (x  4)(x2
 x 4  42
)

42. Ex: 8y3
125
 ((2y)3
 53
)
Apply the rule for difference of cubes:
a
3
 b
3
 a  b  a
2
 ab  b
2
 
 2y  5  2y 2
 2y 5 5 
2
 
 2y  5  4y
2
10 y  25 

43. Quadratic Formula
The quadratic formula is used to solve any quadratic equation.
2
4
2
x
cb b a
a
  

The quadratic formula is:
Standard form of a quadratic equation is: 2
0x xba c  

44. Real word Problem:
Given the diagram below, approximate to the nearest foot how many feet
of walking distance a person saves by cutting across the lawn instead of
walking on the sidewalk.

45. Given the diagram below, approximate to the nearest foot how many feet of
walking distance a person saves by cutting across the lawn instead of walking on
the sidewalk.
x + 2
x
The Pythagorean Theorem
a2 + b2 = c2
(x + 2)2 + x2 = 202
x2 + 4x + 4 + x2 = 400
2x2 + 4x + 4 = 400
2x2 + 4x – 369 = 0
2(x2 + 2x – 198) = 0

46. 2(x2 + 2x – 198) = 0
    
 12
1981422
2

x
2
79242 
x
2
7962 
x
x + 2
x

47. x + 2
x



2
7962
x 

2
2.282
2
2.282
x
2
2.282
x
2
2.26
x
1.13x
2
2.30
x
1.15xft

48. x + 2
x
1.13x
ft2.28
ft
 21.131.132x
28 – 20 = 8 ft

49. Real Word Problems:
Q 1: A ball is thrown straight up, from 3 m above the ground, with a
velocity of 14 m/s. When does it hit the ground?

50.  Q 2: A Company is going to make frames as part of a new product
they are launching.
The frame will be cut out of a piece of steel, and to keep the weight
down, the final area should be 28 cm2.
The inside of the frame has to be 11 cm by 6 cm.
What should the width x of the metal be.

51. Q 3: Two resistors are in parallel, like in this diagram:
The total resistance has been
measured at 2 Ohms, and one of the
resistors is known to be 3 ohms
more than the other.
What are the values of the two resistors?
The formula to work out total resistance "RT" is:
1/RT = 1/R1 + 1/R2

52. Q 4: An object is thrown downward with an initial
velocity of 19 feet per second. The distance, d it travels
in an amount of time, t is given by the equation d=19t
+15𝑡2
. How long does it take the object to fall 50 feet?

53. Q 5: A 3 hour river cruise goes 15 km upstream and then
back again. The river has a current of 2 km an hour. What
is the boat's speed and how long was the upstream
journey?