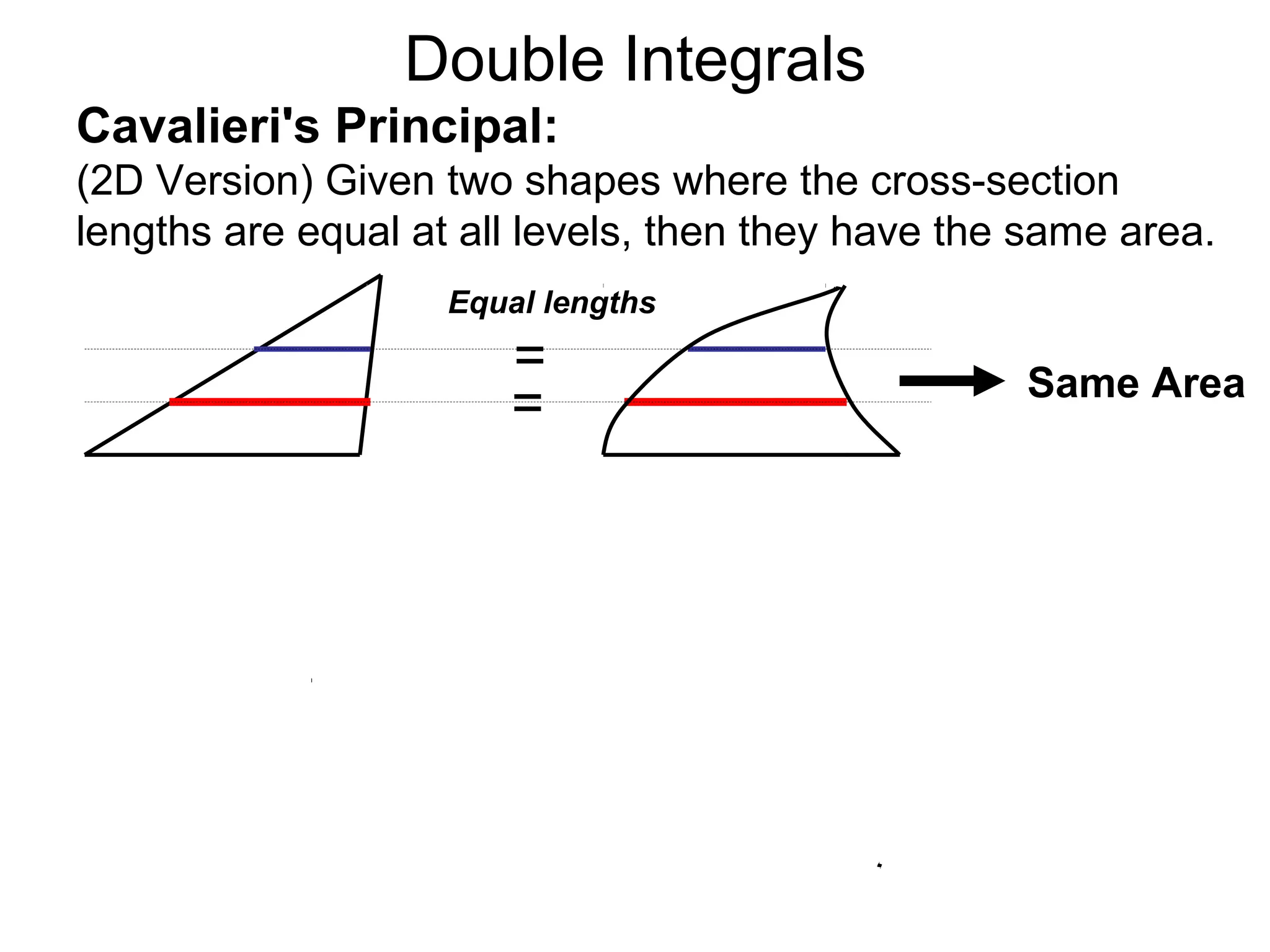
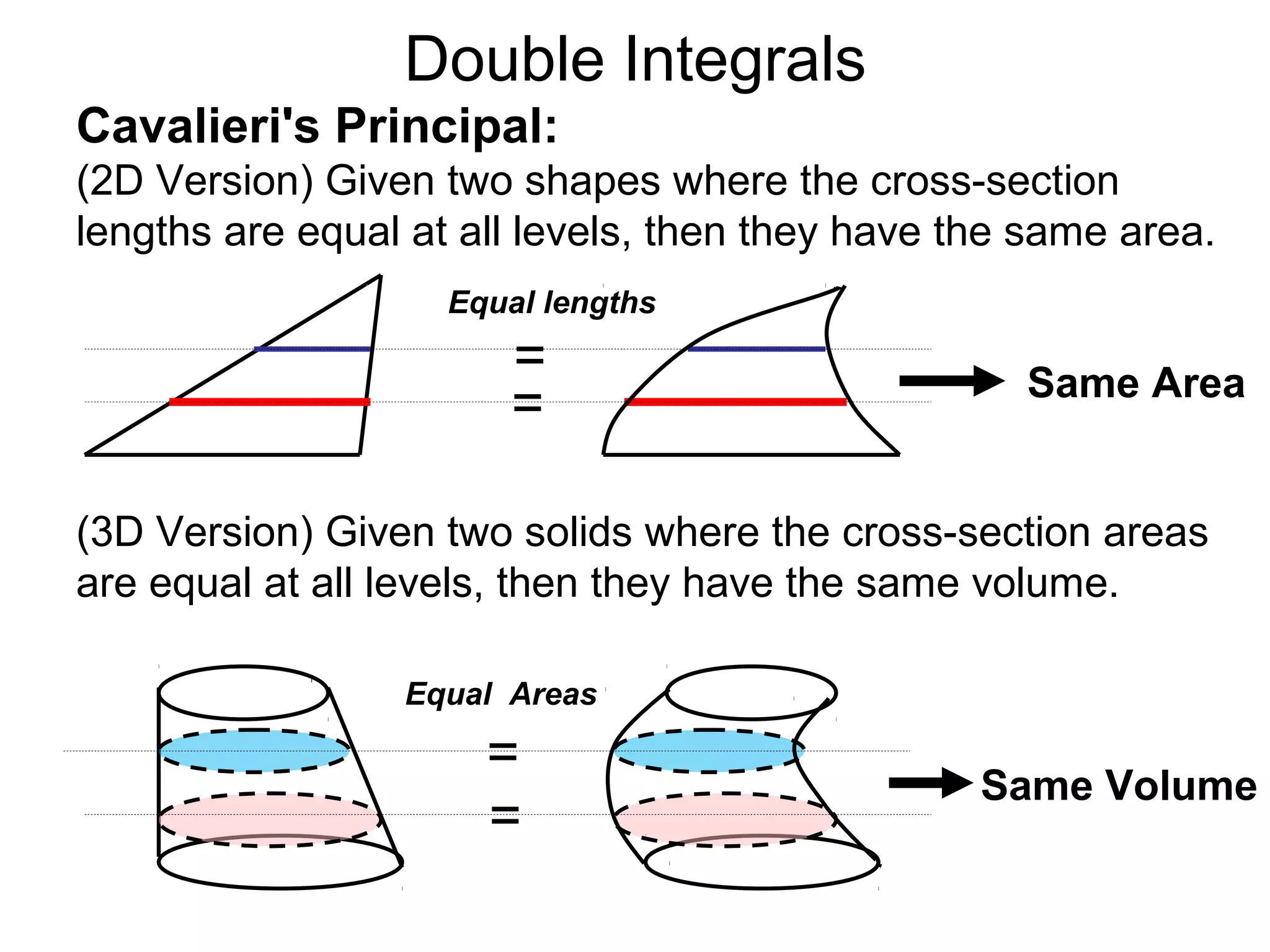
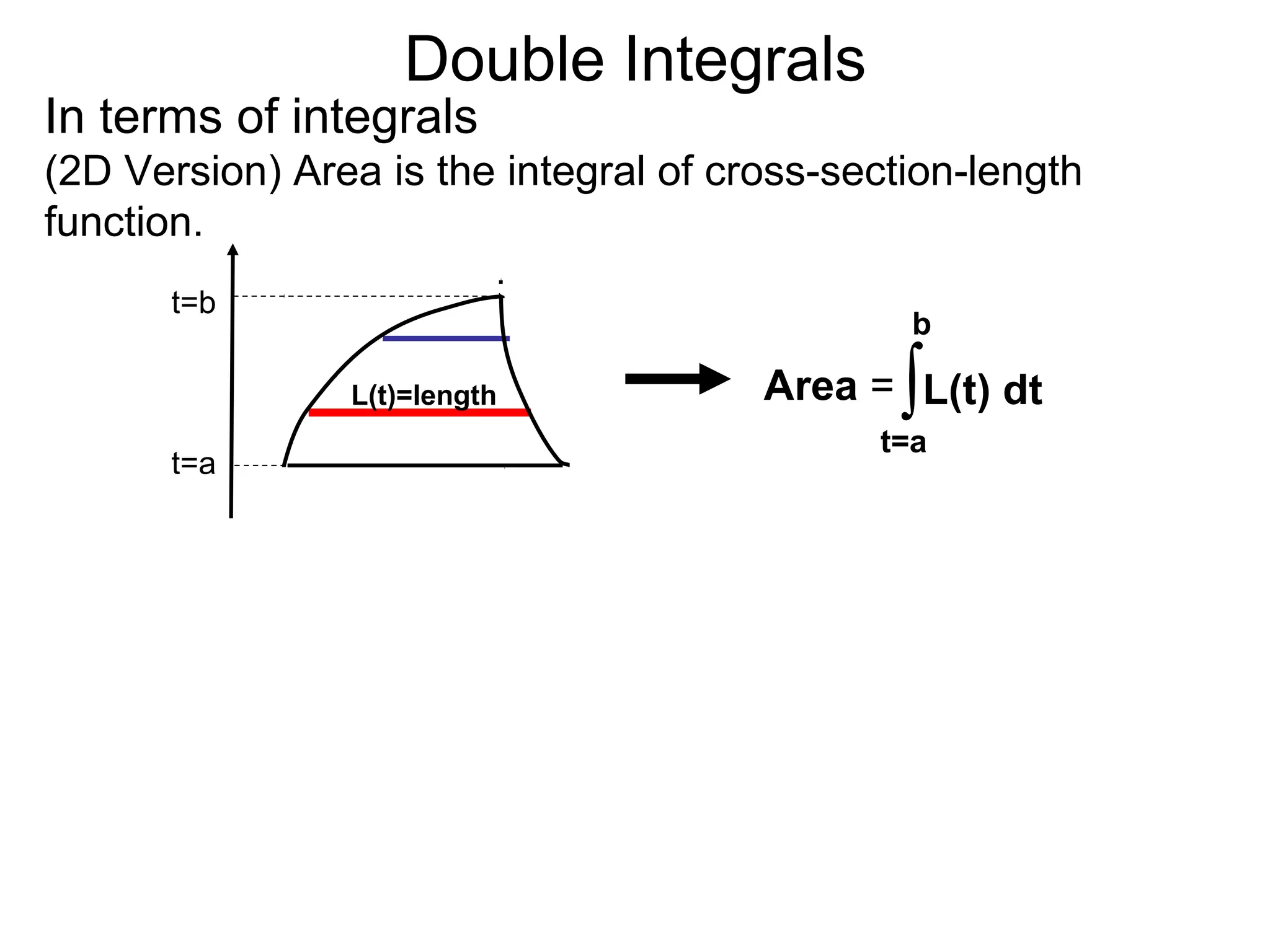
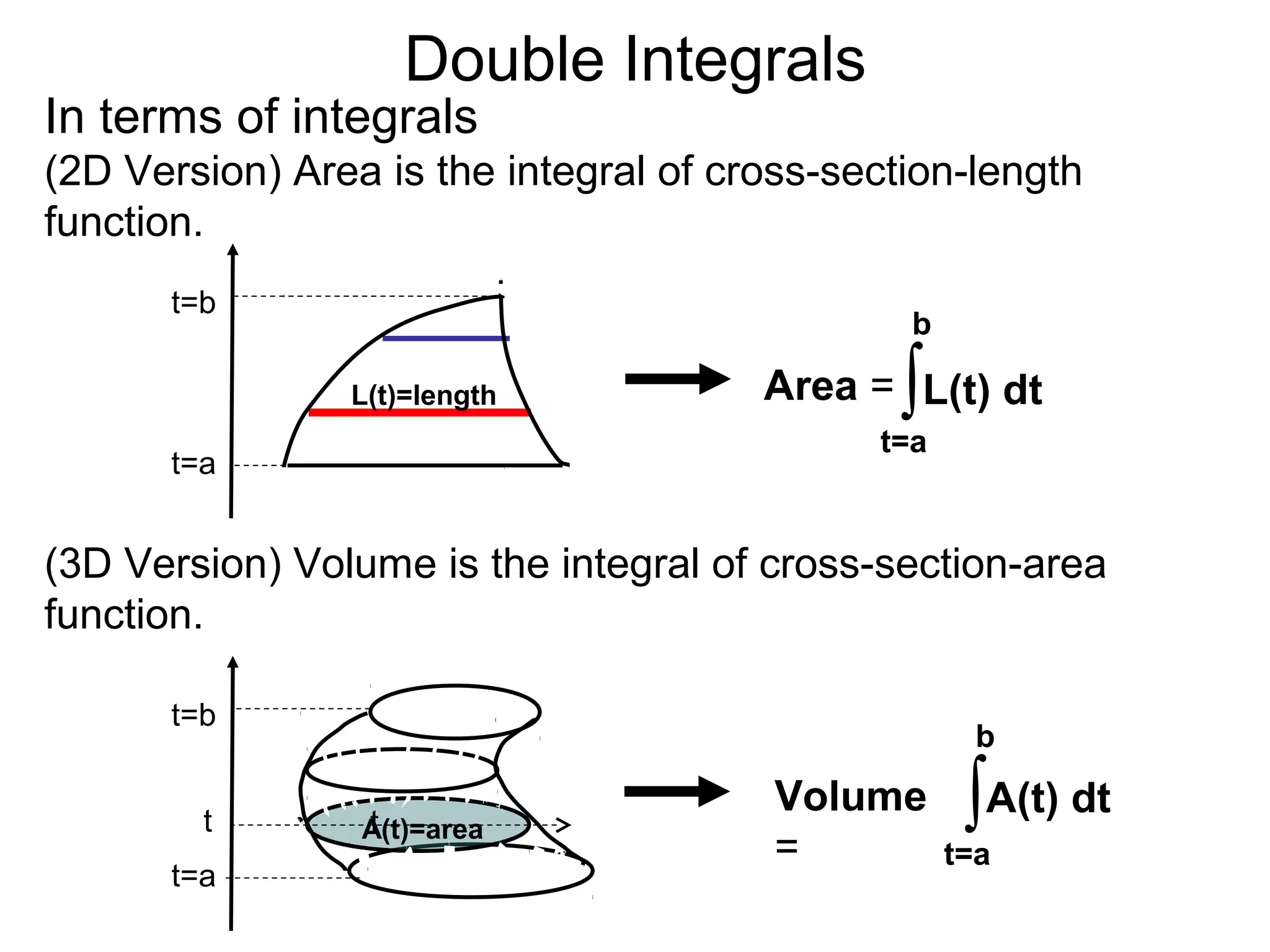
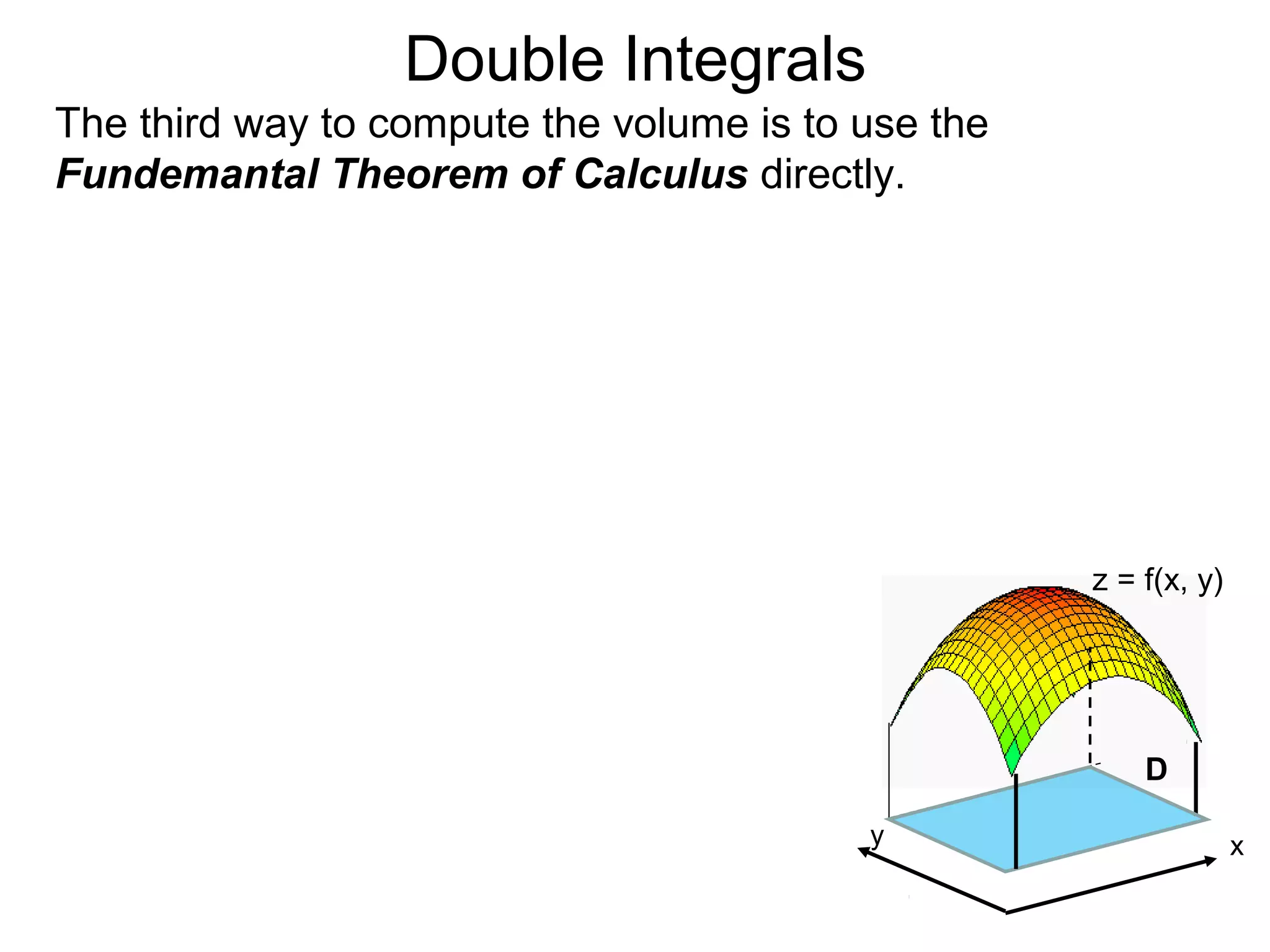
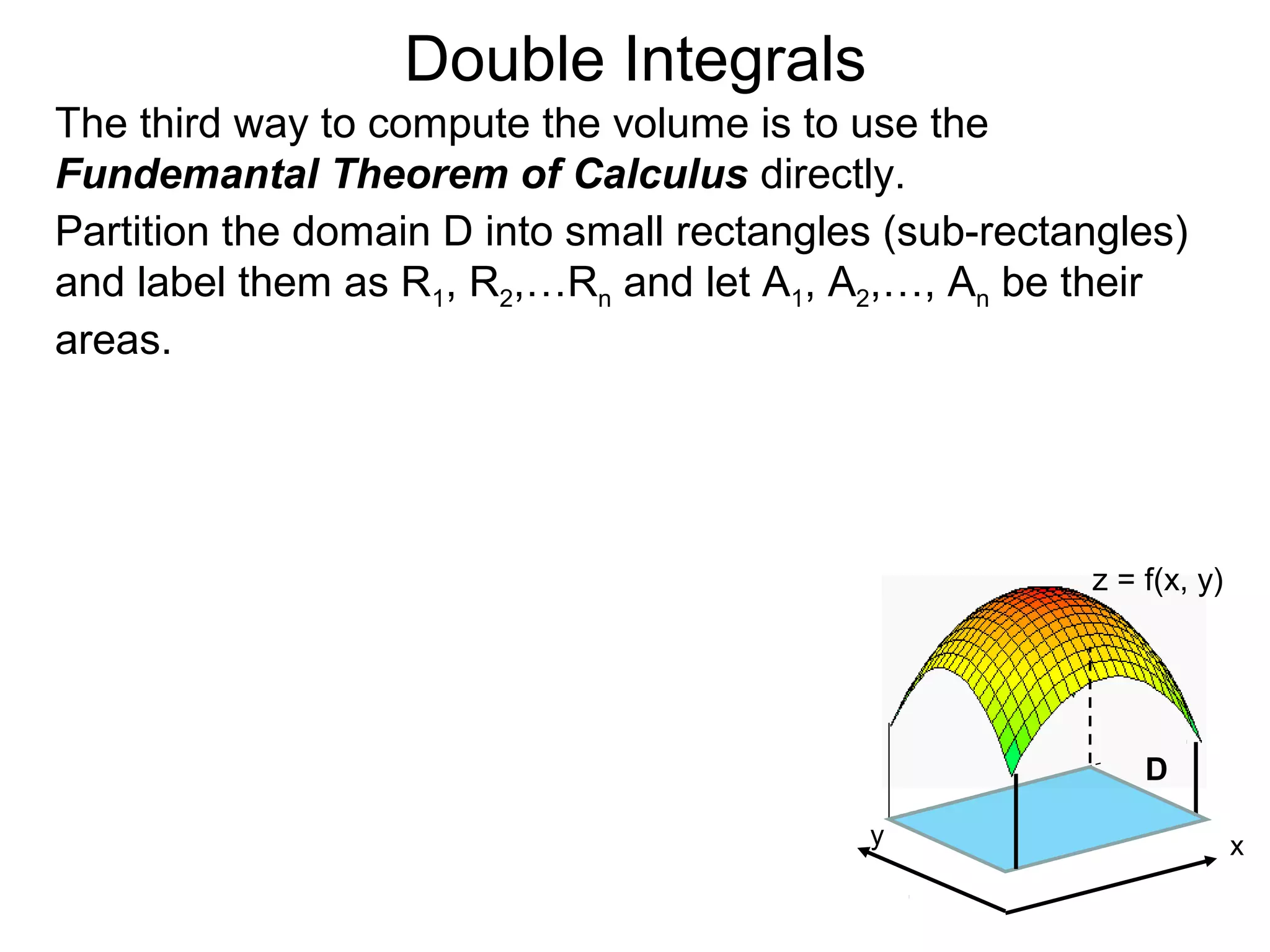
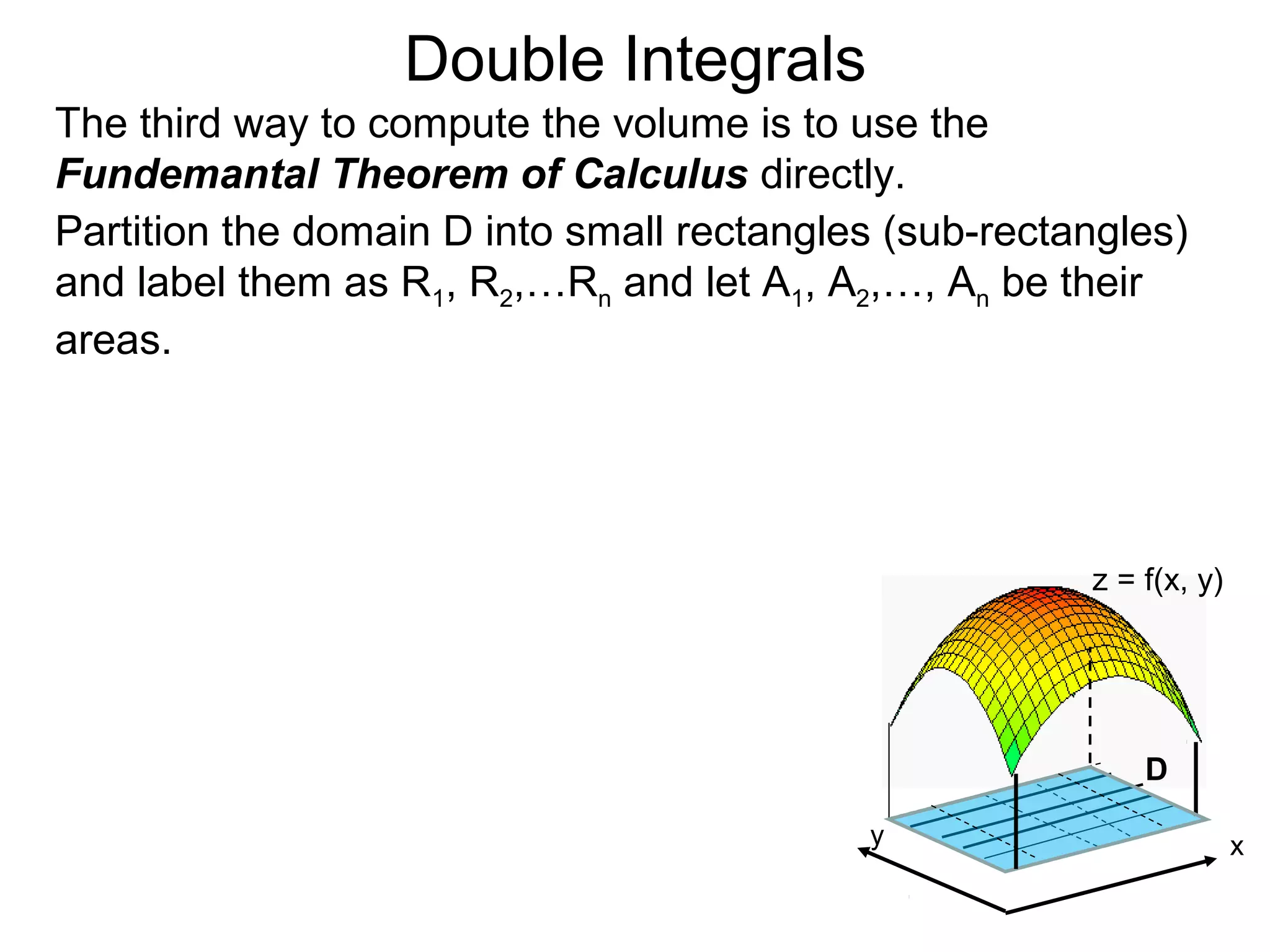
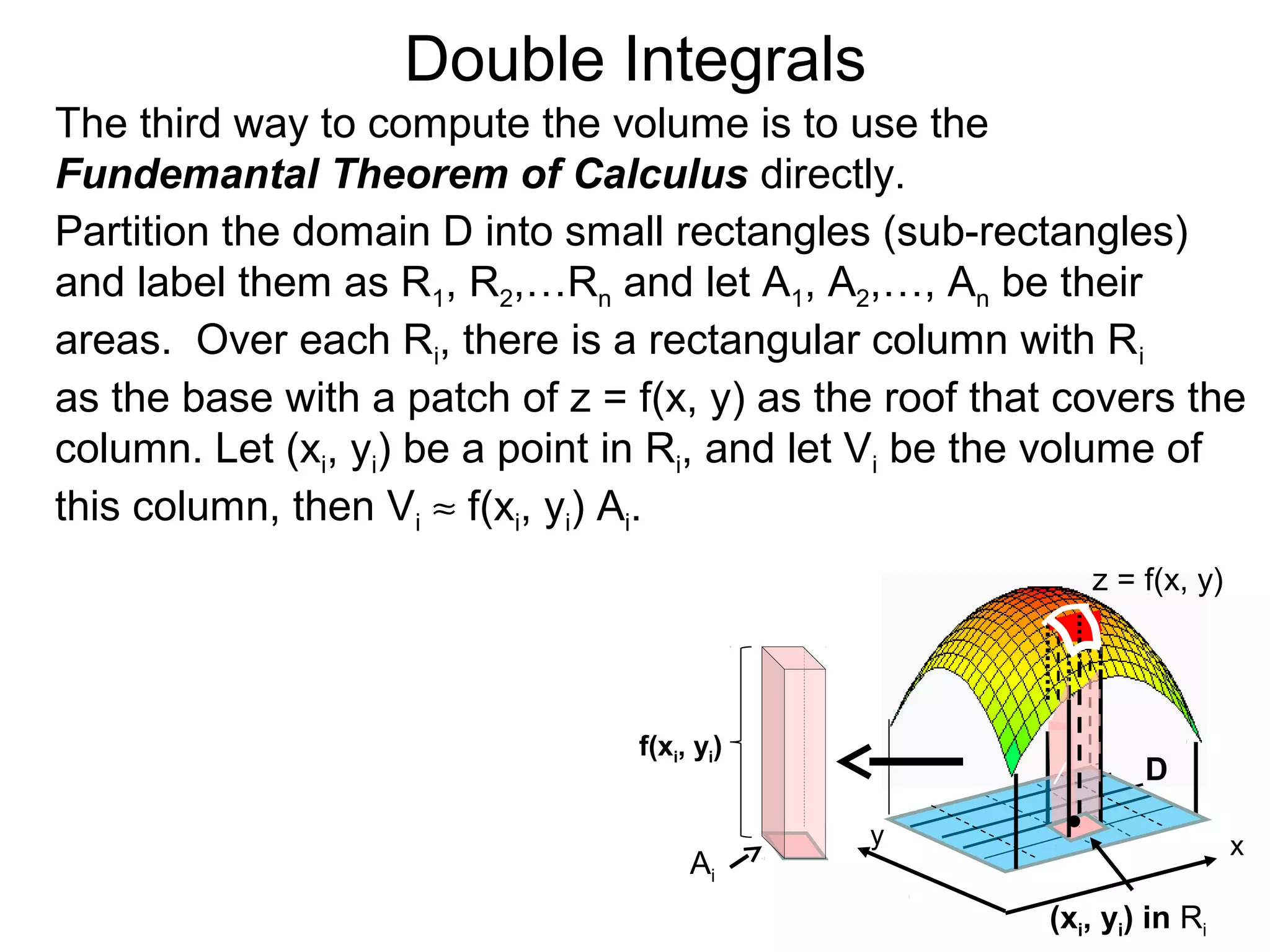
The document discusses double integrals and their use in calculating volumes. It explains that double integrals allow calculating the volume of a solid over a domain D by integrating the height function f(x,y) over D. Three methods are provided: integrating cross-sectional areas A(x) or A(y) with respect to x or y; directly using the fundamental theorem of calculus by partitioning D into subrectangles and summing the approximate volumes; and writing the calculation as a double integral of f(x,y) over D.

1. Double Integrals

2. Double Integrals
Cavalieri's Principal:
(2D Version) Given two shapes where the cross-section
lengths are equal at all levels, then they have the same area.
=
= Same Area
Equal lengths

3. Double Integrals
Cavalieri's Principal:
(2D Version) Given two shapes where the cross-section
lengths are equal at all levels, then they have the same area.
(3D Version) Given two solids where the cross-section areas
are equal at all levels, then they have the same volume.
=
=
=
=
Same Area
Same Volume
Equal lengths
Equal Areas

4. Double Integrals
In terms of integrals
(2D Version) Area is the integral of cross-section-length
function.
Area =
t=b
t=a
L(t)=length
t=a
b
L(t) dt∫

5. Double Integrals
In terms of integrals
(2D Version) Area is the integral of cross-section-length
function.
Area =
t=b
t=a
L(t)=length
t=a
b
L(t) dt
t=b
t=a
A(t)=area
(3D Version) Volume is the integral of cross-section-area
function.
∫
t=a
b
A(t) dtVolume
=
∫tt

6. Double Integrals
We write the rectangular area
{(x, y)| a ≤ x ≤ b and c ≤ y ≤ d}
as [a, b] x [c, d]. a b
c
d
[a, b] x [c, d]

7. Double Integrals
Given z = f(x, y) ≥ 0 over the domain D = [a, b] x [c, d],
it defines a solid over D.
x
y
We write the rectangular area
{(x, y)| a ≤ x ≤ b and c ≤ y ≤ d}
as [a, b] x [c, d].
z = f(x, y)
a
b
c
d
D
a b
c
d
[a, b] x [c, d]
D

8. Double Integrals
Given z = f(x, y) ≥ 0 over the domain D = [a, b] x [c, d],
it defines a solid over D. Hence the volume V of this solid is
x
y
We write the rectangular area
{(x, y)| a ≤ x ≤ b and c ≤ y ≤ d}
as [a, b] x [c, d].
z = f(x, y)
a
b
c
d
D
a b
c
d
[a, b] x [c, d]
D
x=a
b
A(x) dx, where A(x) is the cross-sectional area
function.
V = ∫

9. Double Integrals
Given z = f(x, y) ≥ 0 over the domain D = [a, b] x [c, d],
it defines a solid over D. Hence the volume V of this solid is
x
y
We write the rectangular area
{(x, y)| a ≤ x ≤ b and c ≤ y ≤ d}
as [a, b] x [c, d].
z = f(x, y)
a
b
c
d
D
x
a b
c
d
[a, b] x [c, d]
A(x)
D
x=a
b
A(x) dx, where A(x) is the cross-sectional area
function.
V = ∫

10. Double Integrals
Given z = f(x, y) ≥ 0 over the domain D = [a, b] x [c, d],
it defines a solid over D. Hence the volume V of this solid is
x
y
We write the rectangular area
{(x, y)| a ≤ x ≤ b and c ≤ y ≤ d}
as [a, b] x [c, d].
z = f(x, y)
a
b
c
d
D
x
a b
c
d
[a, b] x [c, d]
A(x)
D
x=a
b
A(x) dx, where A(x) is the cross-sectional area
function.
V =
d
∫
On the other hand A(x) =
y=c
f(x, y) dy
where the integral is taken by
treating x as a constant.
∫

11. Double Integrals
Given z = f(x, y) ≥ 0 over the domain D = [a, b] x [c, d],
it defines a solid over D. Hence the volume V of this solid is
x
y
We write the rectangular area
{(x, y)| a ≤ x ≤ b and c ≤ y ≤ d}
as [a, b] x [c, d].
z = f(x, y)
a
b
c
d
D
x
Hence the volume V is
V = [
x=a
x=b
dx.
y=c
y=d
f(x, y) dy ]∫ ∫
a b
c
d
[a, b] x [c, d]
A(x)
D
x=a
b
A(x) dx, where A(x) is the cross-sectional area
function.
V =
d
∫
On the other hand A(x) =
y=c
f(x, y) dy
where the integral is taken by
treating x as a constant.
∫

12. Double Integrals
x
y
z = f(x, y)
a
b
c
d
D
x
A(x)
D
f(x, y) dy ] dxThe integral
is called the double integral with respect to y then x.
f(x, y) dy dx =∫∫ ∫ ∫[ A(x) dx∫=

13. Double Integrals
x
y
z = f(x, y)
a
b
c
d
D
x
A(x)
D
f(x, y) dy ] dxThe integral
is called the double integral with respect to y then x.
f(x, y) dy dx =∫∫ ∫ ∫[
f(x, y) dx ] dySimilarly,
is called the double integral with respect to x then y.
f(x, y) dx dy =∫∫ ∫ ∫[
A(x) dx∫=
A(y) dy∫=

14. Double Integrals
x
y
z = f(x, y)
a
b
c
d
D
x
A(x)
D
f(x, y) dy ] dxThe integral
is called the double integral with respect to y then x.
f(x, y) dy dx =∫∫ ∫ ∫[
x
y
z = f(x, y)
a
b
c
d
D
y
A(y)
f(x, y) dx ] dySimilarly,
is called the double integral with respect to x then y.
f(x, y) dx dy =∫∫ ∫ ∫[
It represents the volume integration over the cross sectional
areas A(y) by setting y as a constant
A(x) dx∫=
A(y) dy∫=

15. Double Integrals
x
y
z = f(x, y)
a
b
c
d
D
x
A(x)
D
f(x, y) dy ] dxThe integral
is called the double integral with respect to y then x.
f(x, y) dy dx =∫∫ ∫ ∫[
x
y
z = f(x, y)
a
b
c
d
D
y
A(y)
f(x, y) dx ] dySimilarly,
is called the double integral with respect to x then y.
f(x, y) dx dy =∫∫ ∫ ∫[
f(x, y) dx = A(y)∫ is calculated by treating y as a constant.
It represents the volume integration over the cross sectional
areas A(y) by setting y as a constant and that
A(x) dx∫=
A(y) dy∫=

16. Double Integrals
z = f(x, y)
D
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
xy

17. Double Integrals
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas.
z = f(x, y)
D
xy

18. Double Integrals
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas.
z = f(x, y)
D
xy

19. Double Integrals
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas. Over each Ri, there is a rectangular column with Ri
as the base with a patch of z = f(x, y) as the roof that covers the
column.
z = f(x, y)
D
xy

20. Double Integrals
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas. Over each Ri, there is a rectangular column with Ri
as the base with a patch of z = f(x, y) as the roof that covers the
column.
z = f(x, y)
D
/
y x

21. Double Integrals
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas. Over each Ri, there is a rectangular column with Ri
as the base with a patch of z = f(x, y) as the roof that covers the
column. Let (xi, yi) be a point in Ri, and let Vi be the volume of
this column, then Vi ≈ f(xi, yi) Ai.
z = f(x, y)
D
(xi, yi) in Ri
/
y x

22. Double Integrals
y
z = f(x, y)
D
(xi, yi) in Ri
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas. Over each Ri, there is a rectangular column with Ri
as the base with a patch of z = f(x, y) as the roof that covers the
column. Let (xi, yi) be a point in Ri, and let Vi be the volume of
this column, then Vi ≈ f(xi, yi) Ai.
x
/
Vi ≈ f(xi, yi) Ai
Ai

23. Double Integrals
y
z = f(x, y)
D
(xi, yi) in Ri
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas. Over each Ri, there is a rectangular column with Ri
as the base with a patch of z = f(x, y) as the roof that covers the
column. Let (xi, yi) be a point in Ri, and let Vi be the volume of
this column, then Vi ≈ f(xi, yi) Ai.
x
/
Ai
f(xi, yi)

24. Double Integrals
y
z = f(x, y)
D
(xi, yi) in Ri
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas. Over each Ri, there is a rectangular column with Ri
as the base with a patch of z = f(x, y) as the roof that covers the
column. Let (xi, yi) be a point in Ri, and let Vi be the volume of
this column, then Vi ≈ f(xi, yi) Ai.
x
/
Vi ≈ f(xi, yi) Ai
Ai
f(xi, yi)

25. Double Integrals
y
z = f(x, y)
D
(xi, yi) in Ri
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas. Over each Ri, there is a rectangular column with Ri
as the base with a patch of z = f(x, y) as the roof that covers the
column. Let (xi, yi) be a point in Ri, and let Vi be the volume of
this column, then Vi ≈ f(xi, yi) Ai. The entire volume V
is approximately the sum of all the Vi, that is
x
/
i=1 i=1
nn
V ≈ ∑ Vi = ∑ f(xi, yi) Ai,
Vi ≈ f(xi, yi) Ai
Ai
f(xi, yi)

26. Double Integrals
y
z = f(x, y)
D
(xi, yi) in Ri
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas. Over each Ri, there is a rectangular column with Ri
as the base with a patch of z = f(x, y) as the roof that covers the
column. Let (xi, yi) be a point in Ri, and let Vi be the volume of
this column, then Vi ≈ f(xi, yi) Ai. The entire volume V
is approximately the sum of all the Vi, that is
x
/
i=1 i=1
nn
V = lim ∑ Vi
Ai 0
V ≈ ∑ Vi = ∑ f(xi, yi) Ai, specifically
Vi ≈ f(xi, yi) Ai
Ai
f(xi, yi)

27. Double Integrals
y
z = f(x, y)
D
(xi, yi) in Ri
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas. Over each Ri, there is a rectangular column with Ri
as the base with a patch of z = f(x, y) as the roof that covers the
column. Let (xi, yi) be a point in Ri, and let Vi be the volume of
this column, then Vi ≈ f(xi, yi) Ai. The entire volume V
is approximately the sum of all the Vi, that is
x
/
i=1 i=1
nn
V = lim ∑ Vi = lim ∑f(xi, yi)Ai
Ai 0 Ai 0
V ≈ ∑ Vi = ∑ f(xi, yi) Ai, specifically
if the limit exists.
Vi ≈ f(xi, yi) Ai
Ai
f(xi, yi)

28. Double Integrals
y
z = f(x, y)
D
(xi, yi) in Ri
The third way to compute the volume is to use the
Fundemantal Theorem of Calculus directly.
Partition the domain D into small rectangles (sub-rectangles)
and label them as R1, R2,…Rn and let A1, A2,…, An be their
areas. Over each Ri, there is a rectangular column with Ri
as the base with a patch of z = f(x, y) as the roof that covers the
column. Let (xi, yi) be a point in Ri, and let Vi be the volume of
this column, then Vi ≈ f(xi, yi) Ai. The entire volume V
is approximately the sum of all the Vi, that is
x
/
V = f(x, y) dA.∫∫
i=1 i=1
nn
V = lim ∑ Vi = lim ∑f(xi, yi)Ai
Ai 0 Ai 0
D
V ≈ ∑ Vi = ∑ f(xi, yi) Ai, specifically
if the limit exists. Writing the
above in the integral notation:
Vi ≈ f(xi, yi) Ai
Ai
f(xi, yi)

29. Double Integrals
f(x, y) dx dyThe integral dx andf(x, y) dy ∫∫∫∫ are
called iterated integrals meaning the integral is done one
step at a time.

30. Double Integrals
Theorem: Given z = f(x, y) > 0 a continuous function over the
domnain [a, b] x [c. d], then the following are equal:
f(x, y) dx dyThe integral dx andf(x, y) dy ∫∫∫∫ are
called iterated integrals meaning the integral is done one
step at a time.

31. Double Integrals
Theorem: Given z = f(x, y) > 0 a continuous function over the
domnain [a, b] x [c. d], then the following are equal:
[
x=a
b
dy
y=c
d
f(x, y) dx ]∫∫V = f(x, y) dA =∫∫D
= [
x=a
b
dx
y=c
d
f(x, y) dy ]∫ ∫
f(x, y) dx dyThe integral dx andf(x, y) dy ∫∫∫∫ are
called iterated integrals meaning the integral is done one
step at a time.

32. Double Integrals
Theorem: Given z = f(x, y) > 0 a continuous function over the
domnain [a, b] x [c. d], then the following are equal:
Example: Fid the volume of z = f(x, y) = -2x – y + 6 over the
domain [1, 2] x [2, 3]
f(x, y) dx dyThe integral dx andf(x, y) dy ∫∫∫∫ are
called iterated integrals meaning the integral is done one
step at a time.
[
x=a
b
dy
y=c
d
f(x, y) dx ]∫∫V = f(x, y) dA =∫∫D
= [
x=a
b
dx
y=c
d
f(x, y) dy ]∫ ∫

33. Double Integrals
Theorem: Given z = f(x, y) > 0 a continuous function over the
domnain [a, b] x [c. d], then the following are equal:
Example: Fid the volume of z = f(x, y) = -2x – y + 6 over the
domain [1, 2] x [2, 3]
x
y
6
6
3
1
2
2 3
f(x, y) dx dyThe integral dx andf(x, y) dy ∫∫∫∫ are
called iterated integrals meaning the integral is done one
step at a time.
[
x=a
b
dy
y=c
d
f(x, y) dx ]∫∫V = f(x, y) dA =∫∫D
= [
x=a
b
dx
y=c
d
f(x, y) dy ]∫ ∫

34. Double Integrals
Theorem: Given z = f(x, y) > 0 a continuous function over the
domnain [a, b] x [c. d], then the following are equal:
Example: Fid the volume of z = f(x, y) = -2x – y + 6 over the
domain [1, 2] x [2, 3]
x
y
6
6
3
1
2
2 3
The volume is
x=1
2
dx
y=2
3
-2x – y + 6 dy∫ ∫
f(x, y) dx dyThe integral dx andf(x, y) dy ∫∫∫∫ are
called iterated integrals meaning the integral is done one
step at a time.
[
x=a
b
dy
y=c
d
f(x, y) dx ]∫∫V = f(x, y) dA =∫∫D
= [
x=a
b
dx
y=c
d
f(x, y) dy ]∫ ∫

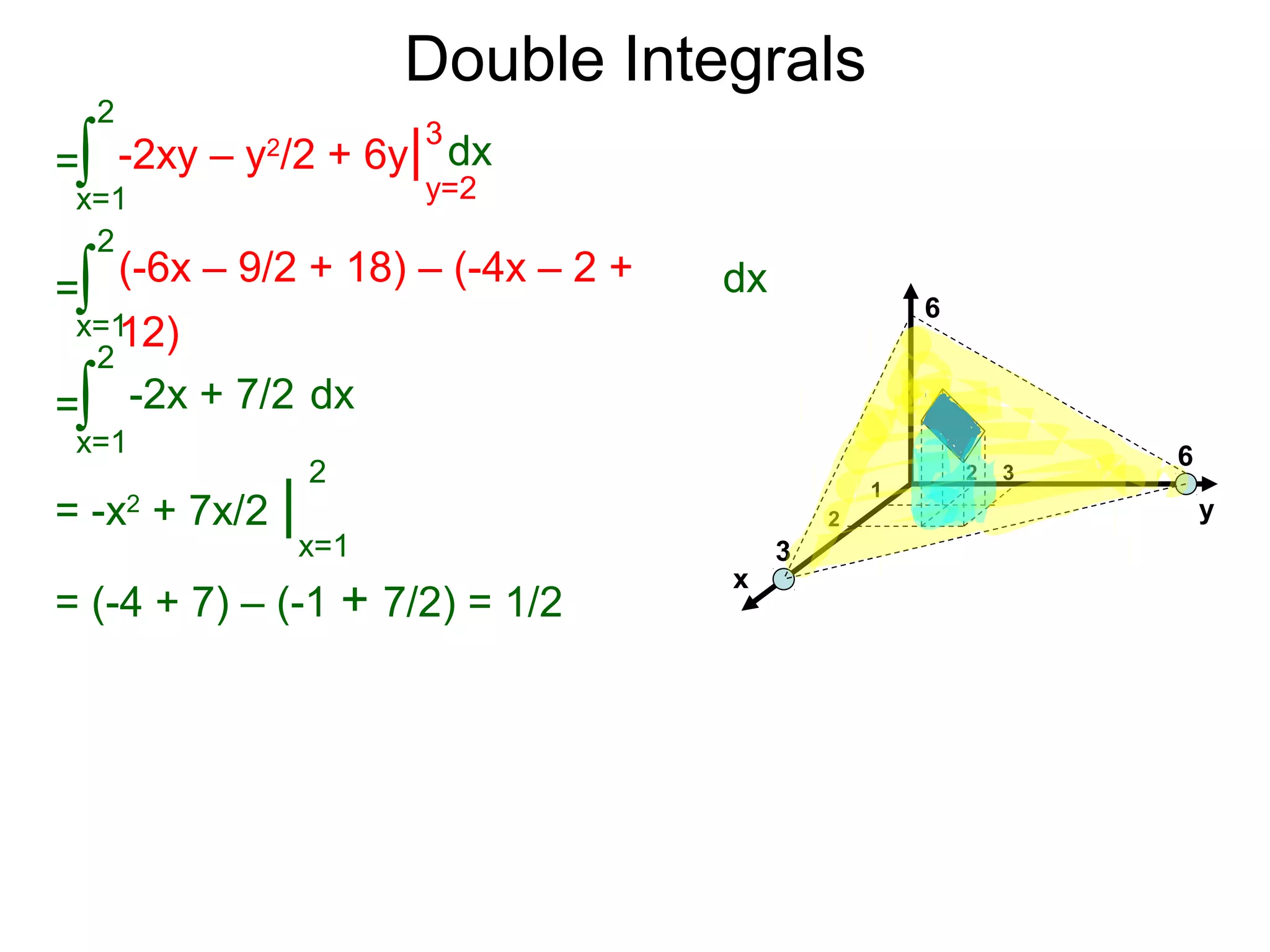
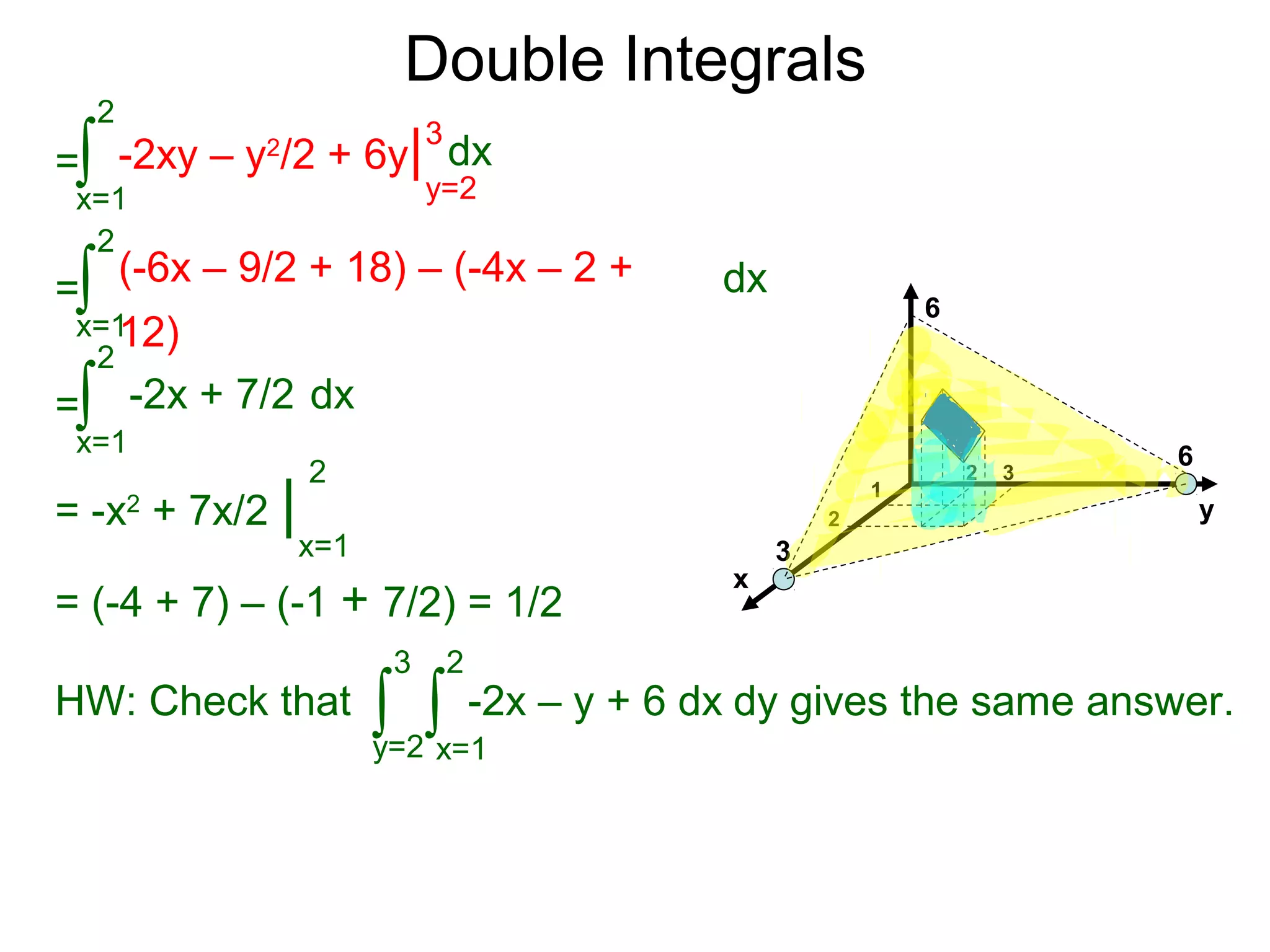
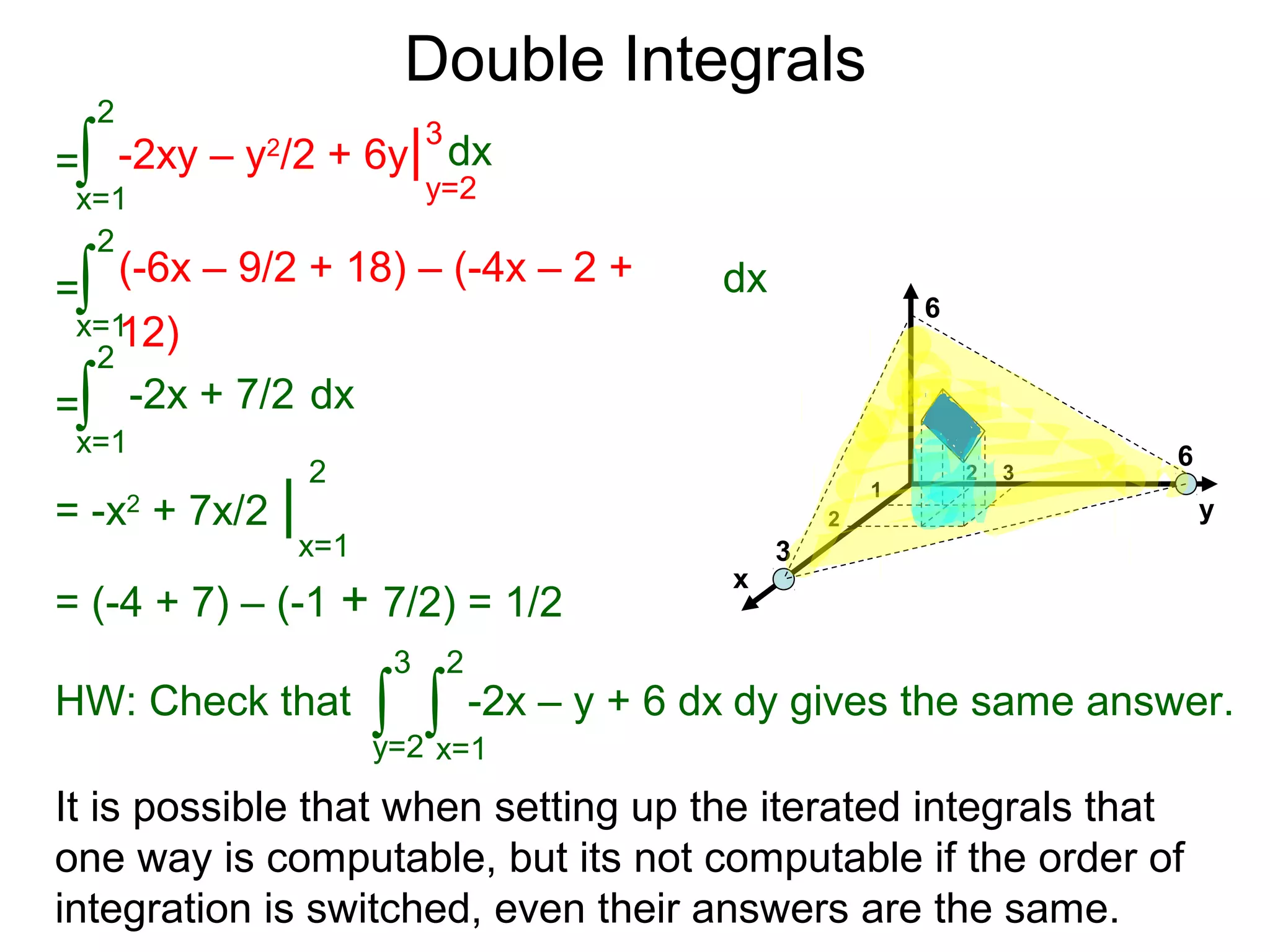
35. Double Integrals
Theorem: Given z = f(x, y) > 0 a continuous function over the
domnain [a, b] x [c. d], then the following are equal:
Example: Fid the volume of z = f(x, y) = -2x – y + 6 over the
domain [1, 2] x [2, 3]
x
y
6
6
3
1
2
2 3
The volume is
x=1
2
dx
y=2
3
-2x – y + 6 dy∫ ∫
=
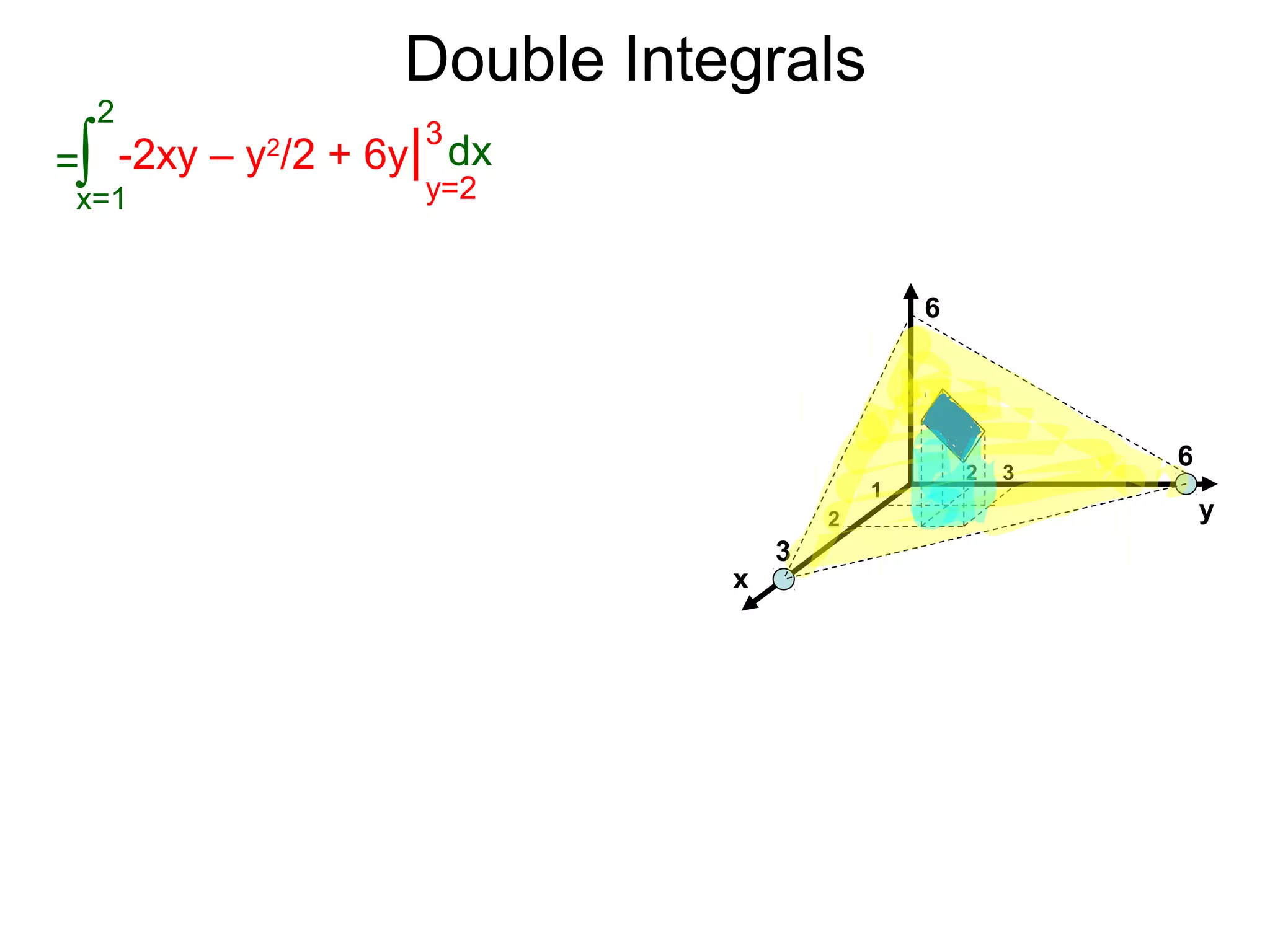
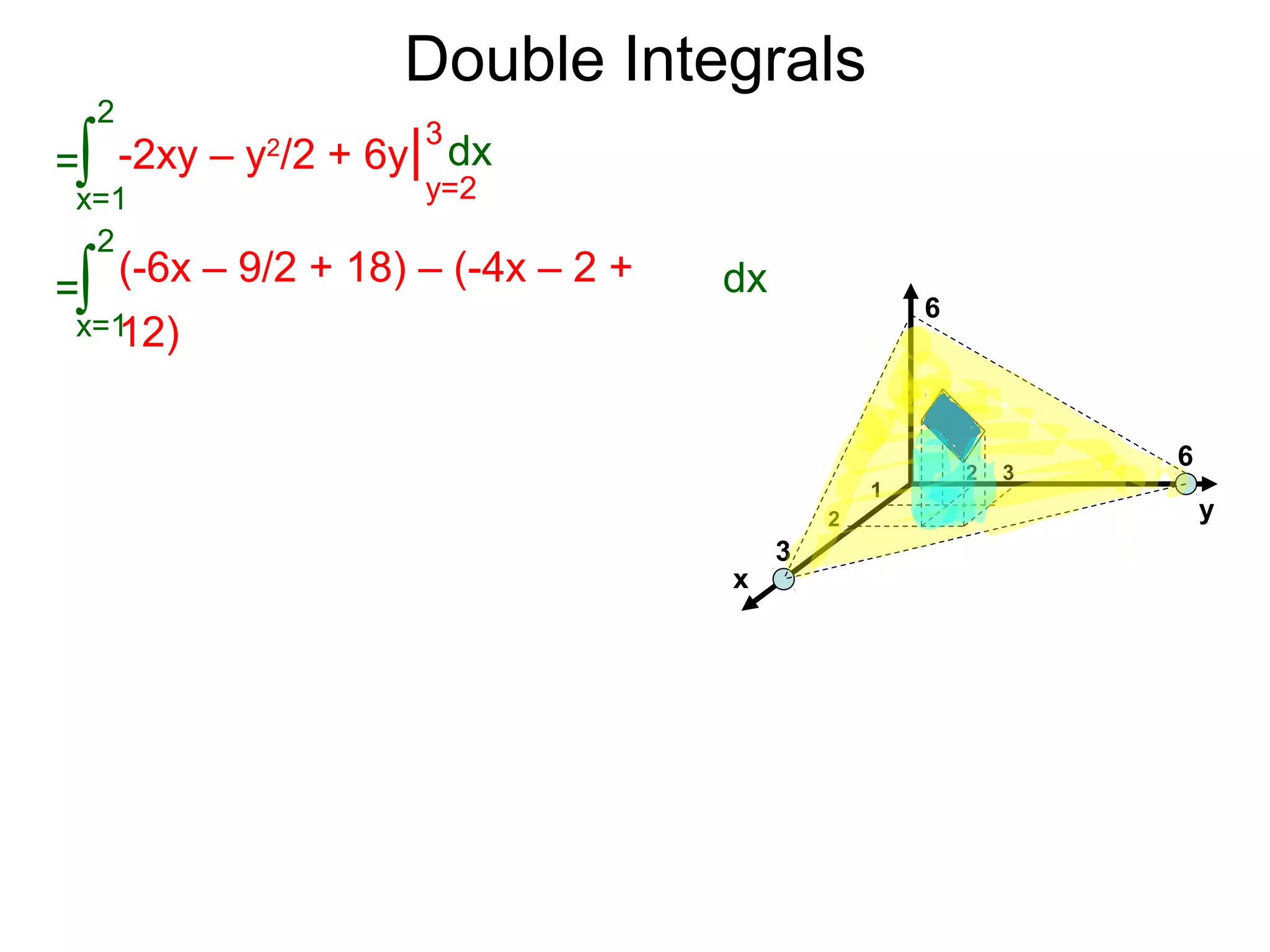
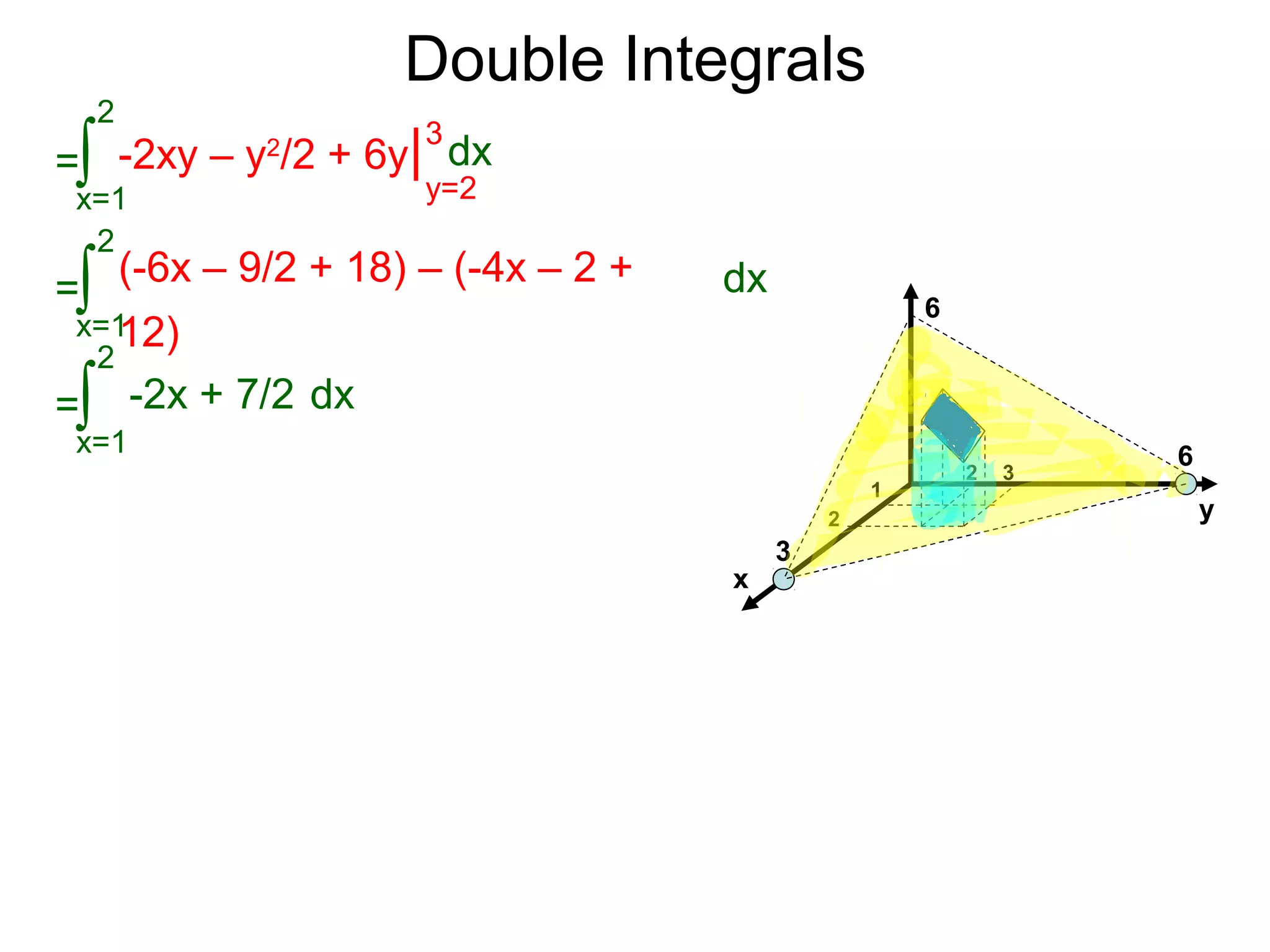
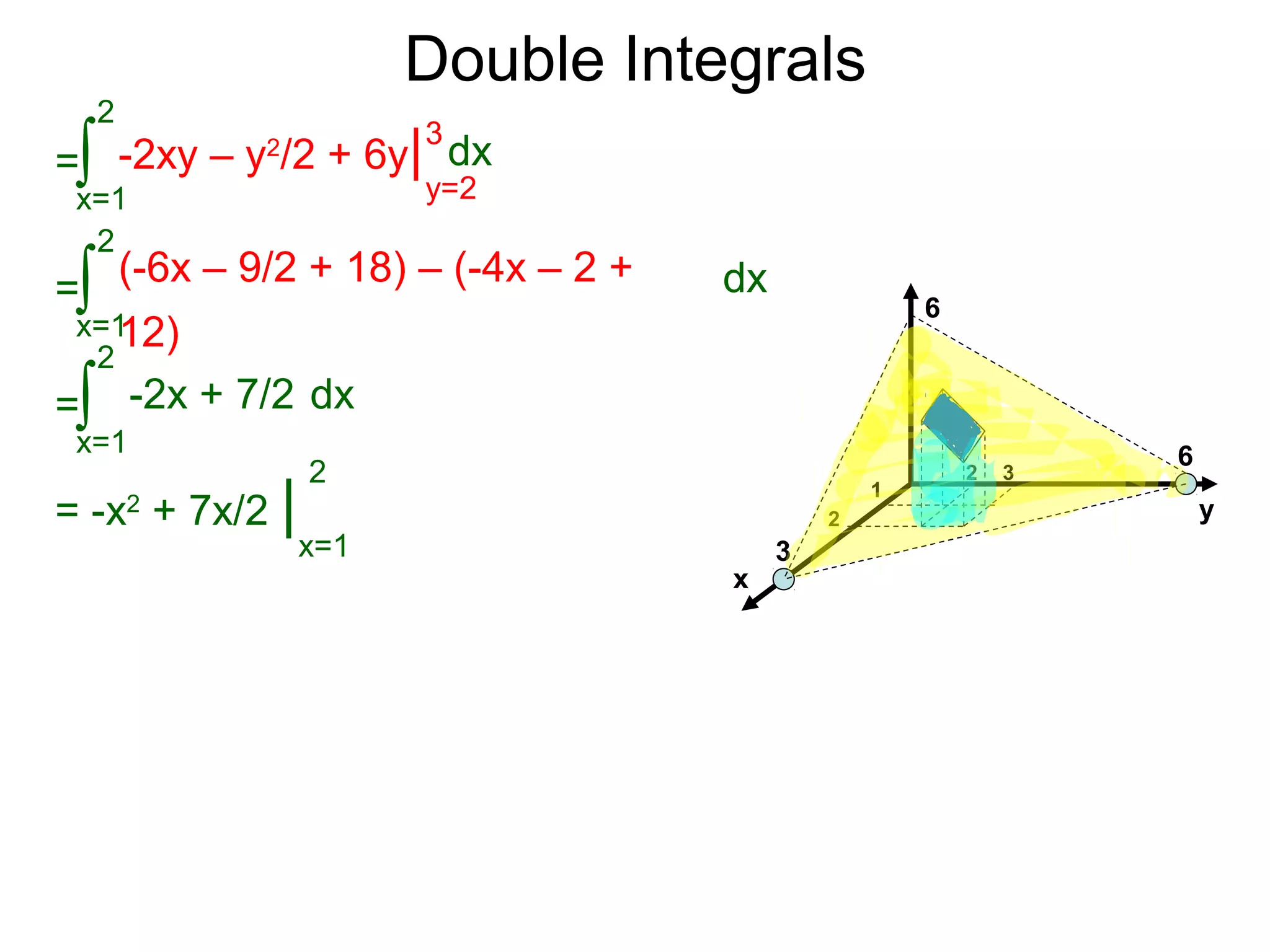
x=1
2
∫ -2xy – y2
/2 + 6y| dx
y=2
3
f(x, y) dx dyThe integral dx andf(x, y) dy ∫∫∫∫ are
called iterated integrals meaning the integral is done one
step at a time.
[
x=a
b
dy
y=c
d
f(x, y) dx ]∫∫V = f(x, y) dA =∫∫D
= [
x=a
b
dx
y=c
d
f(x, y) dy ]∫ ∫

36. Double Integrals
x
y
6
6
3
1
2
2 3
=
x=1
2
∫ -2xy – y2
/2 + 6y| dx
y=2
3

37. Double Integrals
x
y
6
6
3
1
2
2 3
=
x=1
2
∫ -2xy – y2
/2 + 6y| dx
y=2
3
=
x=1
2
∫ (-6x – 9/2 + 18) – (-4x – 2 +
12)
dx

38. Double Integrals
x
y
6
6
3
1
2
2 3
=
x=1
2
∫ -2xy – y2
/2 + 6y| dx
y=2
3
=
x=1
2
∫ (-6x – 9/2 + 18) – (-4x – 2 +
12)
dx
=
x=1
2
∫ -2x + 7/2 dx

39. Double Integrals
x
y
6
6
3
1
2
2 3
=
x=1
2
∫ -2xy – y2
/2 + 6y| dx
y=2
3
=
x=1
2
∫ (-6x – 9/2 + 18) – (-4x – 2 +
12)
dx
=
x=1
2
∫ -2x + 7/2 dx
= -x2
+ 7x/2 |
x=1
2

40. Double Integrals
x
y
6
6
3
1
2
2 3
=
x=1
2
∫ -2xy – y2
/2 + 6y| dx
y=2
3
=
x=1
2
∫ (-6x – 9/2 + 18) – (-4x – 2 +
12)
dx
=
x=1
2
∫ -2x + 7/2 dx
= -x2
+ 7x/2 |
x=1
2
= (-4 + 7) – (-1 + 7/2) = 1/2

41. Double Integrals
x
y
6
6
3
1
2
2 3
=
x=1
2
∫ -2xy – y2
/2 + 6y| dx
y=2
3
=
x=1
2
∫ (-6x – 9/2 + 18) – (-4x – 2 +
12)
dx
=
x=1
2
∫ -2x + 7/2 dx
= -x2
+ 7x/2 |
x=1
2
= (-4 + 7) – (-1 + 7/2) = 1/2
HW: Check that
2
dy gives the same answer.
3
-2x – y + 6 dx∫ ∫x=1y=2

42. Double Integrals
x
y
6
6
3
1
2
2 3
=
x=1
2
∫ -2xy – y2
/2 + 6y| dx
y=2
3
=
x=1
2
∫ (-6x – 9/2 + 18) – (-4x – 2 +
12)
dx
=
x=1
2
∫ -2x + 7/2 dx
= -x2
+ 7x/2 |
x=1
2
= (-4 + 7) – (-1 + 7/2) = 1/2
HW: Check that
2
dy gives the same answer.
3
-2x – y + 6 dx∫ ∫x=1y=2
It is possible that when setting up the iterated integrals that
one way is computable, but its not computable if the order of
integration is switched, even their answers are the same.

43. Double Integrals
Example: Find the where D = [0, 1] x [0, 1]
D
ex+2y
dA∫ ∫

44. Double Integrals
Since ex+2y
is continuous, we may change the integral to
an iterated integral, say
0
1
dy
1
ex+2y
dx∫ ∫x=0
Example: Find the where D = [0, 1] x [0, 1]
D
ex+2y
dA∫ ∫

45. Double Integrals
Since ex+2y
is continuous, we may change the integral to
an iterated integral, say
0
1
dy
1
ex+2y
dx∫ ∫x=0
=
0
1 1
ex+2y
| dy∫ x=0
Example: Find the where D = [0, 1] x [0, 1]
D
ex+2y
dA∫ ∫

46. Double Integrals
Since ex+2y
is continuous, we may change the integral to
an iterated integral, say
0
1
dy
1
ex+2y
dx∫ ∫x=0
=
0
1 1
ex+2y
| dy∫ x=0
=
0
1
e1+2y
– e2y
dy∫
Example: Find the where D = [0, 1] x [0, 1]
D
ex+2y
dA∫ ∫

47. Double Integrals
Since ex+2y
is continuous, we may change the integral to
an iterated integral, say
0
1
dy
1
ex+2y
dx∫ ∫x=0
=
0
1 1
ex+2y
| dy∫ x=0
=
0
1
e1+2y
– e2y
dy∫
= (e1+2y
– e2y
) |
1
y=0
1
2
Example: Find the where D = [0, 1] x [0, 1]
D
ex+2y
dA∫ ∫

48. Double Integrals
Since ex+2y
is continuous, we may change the integral to
an iterated integral, say
0
1
dy
1
ex+2y
dx∫ ∫x=0
=
0
1 1
ex+2y
| dy∫ x=0
=
0
1
e1+2y
– e2y
dy∫
= (e1+2y
– e2y
) |
1
y=0
= [(e3
– e2
) – (e – 1)] =
e3
– e2
– e +1
2
1
2
1
2
Example: Find the where D = [0, 1] x [0, 1]
D
ex+2y
dA∫ ∫

49. Double Integrals
Lastly, we note that using the Fundemantal Theorem of
Calculus to find volume, its not necessary that the D is a
rectangle.

50. Double Integrals
Lastly, we note that using the Fundemantal Theorem of
Calculus to find volume, its not necessary that the D is a
rectangle.
We approximate D with small rectangles (sub-rectangles)
R1, R2,…Rn with A1, A2,…, An be their areas.

51. Double Integrals
Lastly, we note that using the Fundemantal Theorem of
Calculus to find volume, its not necessary that the D is a
rectangle.
We approximate D with small rectangles (sub-rectangles)
R1, R2,…Rn with A1, A2,…, An be their areas.
R1 R3 R3 ...

52. Double Integrals
Lastly, we note that using the Fundemantal Theorem of
Calculus to find volume, its not necessary that the D is a
rectangle.
We approximate D with small rectangles (sub-rectangles)
R1, R2,…Rn with A1, A2,…, An be their areas. Select (xi, yi) a
point in Ri, and let Vi be the volume of the column over Ri,
then Vi ≈ f(xi, yi)*Ai.
R1 R3 R3 ...

53. Double Integrals
Lastly, we note that using the Fundemantal Theorem of
Calculus to find volume, its not necessary that the D is a
rectangle.
We approximate D with small rectangles (sub-rectangles)
R1, R2,…Rn with A1, A2,…, An be their areas. Select (xi, yi) a
point in Ri, and let Vi be the volume of the column over Ri,
then Vi ≈ f(xi, yi)*Ai. The entire volume V is approxmately the
sum of all the Vi : R1 R3 R3 ...

54. Double Integrals
Lastly, we note that using the Fundemantal Theorem of
Calculus to find volume, its not necessary that the D is a
rectangle.
We approximate D with small rectangles (sub-rectangles)
R1, R2,…Rn with A1, A2,…, An be their areas. Select (xi, yi) a
point in Ri, and let Vi be the volume of the column over Ri,
then Vi ≈ f(xi, yi)*Ai. The entire volume V is approxmately the
sum of all the Vi :
We define the volume to be the limit as
the areas of sub-rectangles get smaller
and go to 0,
R1 R3 R3 ...

55. Double Integrals
Lastly, we note that using the Fundemantal Theorem of
Calculus to find volume, its not necessary that the D is a
rectangle.
V = f(x, y) dA.
We approximate D with small rectangles (sub-rectangles)
R1, R2,…Rn with A1, A2,…, An be their areas. Select (xi, yi) a
point in Ri, and let Vi be the volume of the column over Ri,
then Vi ≈ f(xi, yi)*Ai. The entire volume V is approxmately the
sum of all the Vi :
∫∫
We define the volume to be the limit as
the areas of sub-rectangles get smaller
and go to 0, that is:
V = lim ∑ Vi = lim ∑f(xi, yi)Ai if the limit
exists and write it as:
Ai 0 Ai 0
D
R1 R3 R3 ...

56. Double Integrals
Lastly, we note that using the Fundemantal Theorem of
Calculus to find volume, its not necessary that the D is a
rectangle.
V = f(x, y) dA.
We approximate D with small rectangles (sub-rectangles)
R1, R2,…Rn with A1, A2,…, An be their areas. Select (xi, yi) a
point in Ri, and let Vi be the volume of the column over Ri,
then Vi ≈ f(xi, yi)*Ai. The entire volume V is approxmately the
sum of all the Vi :
∫∫
We define the volume to be the limit as
the areas of sub-rectangles get smaller
and go to 0, that is:
V = lim ∑ Vi = lim ∑f(xi, yi)Ai if the limit
exists and write it as:
Ai 0 Ai 0
D
R1 R3 R3 ...
In next section, we will convert this to iterated integrals.