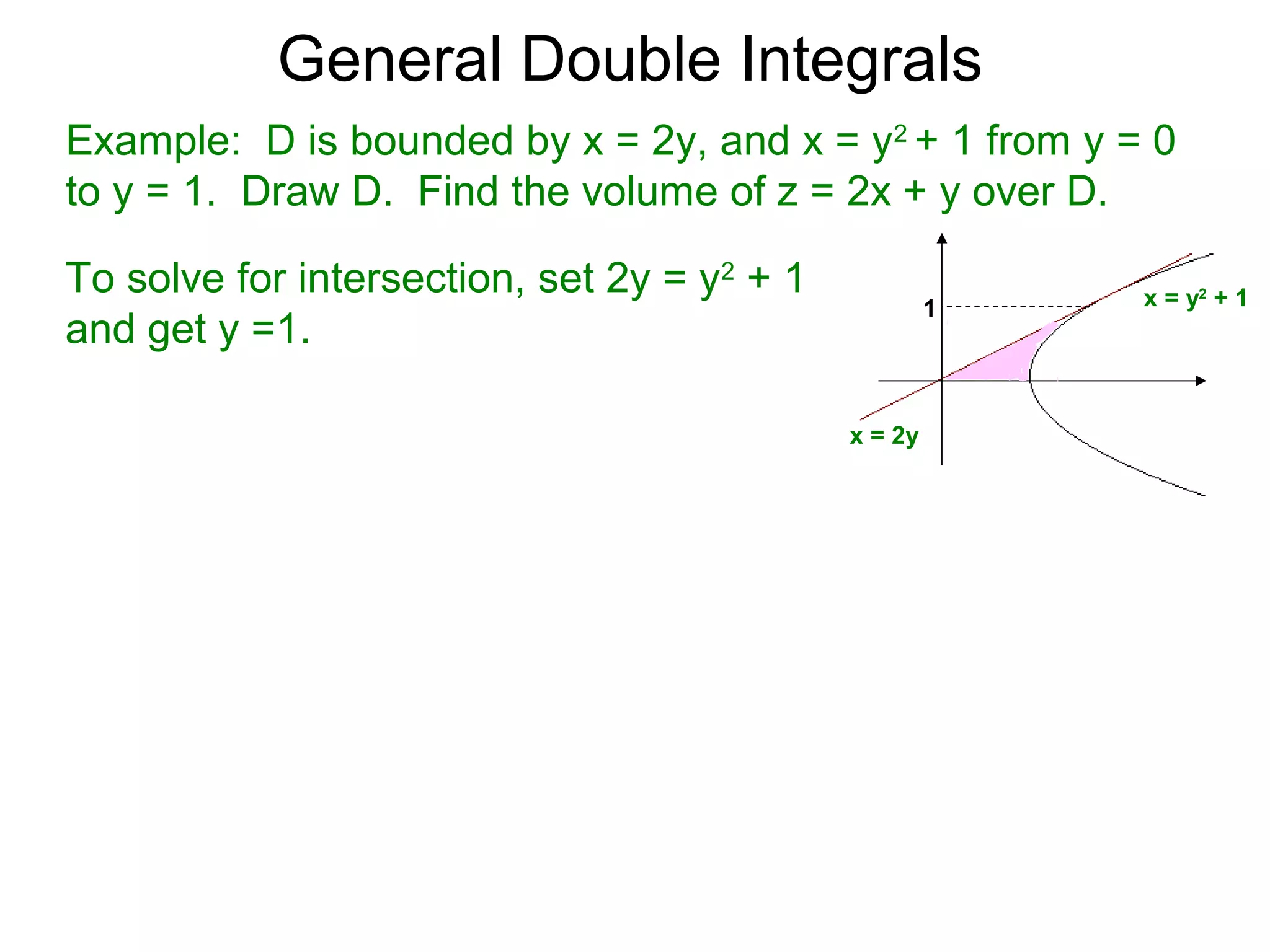
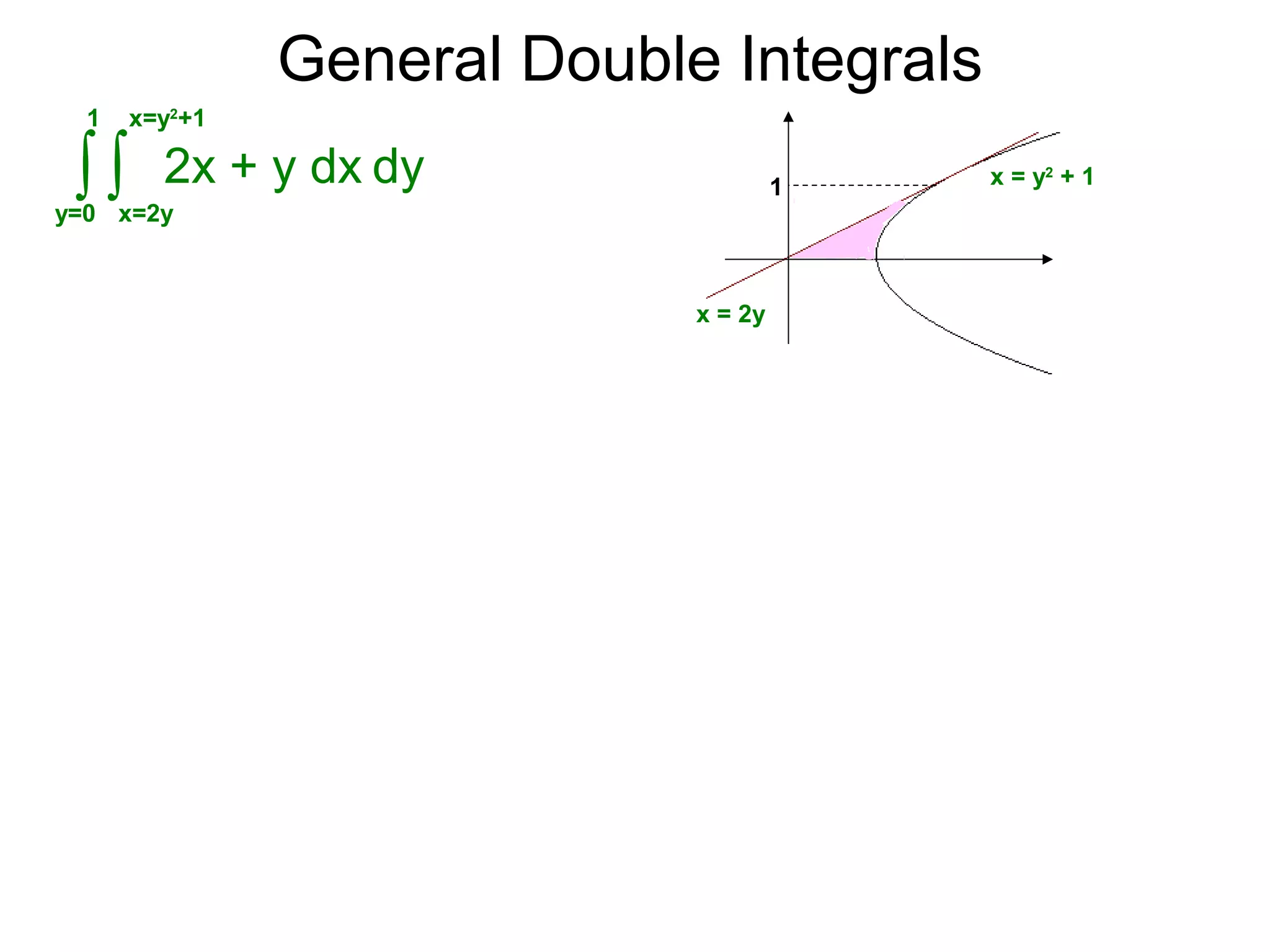
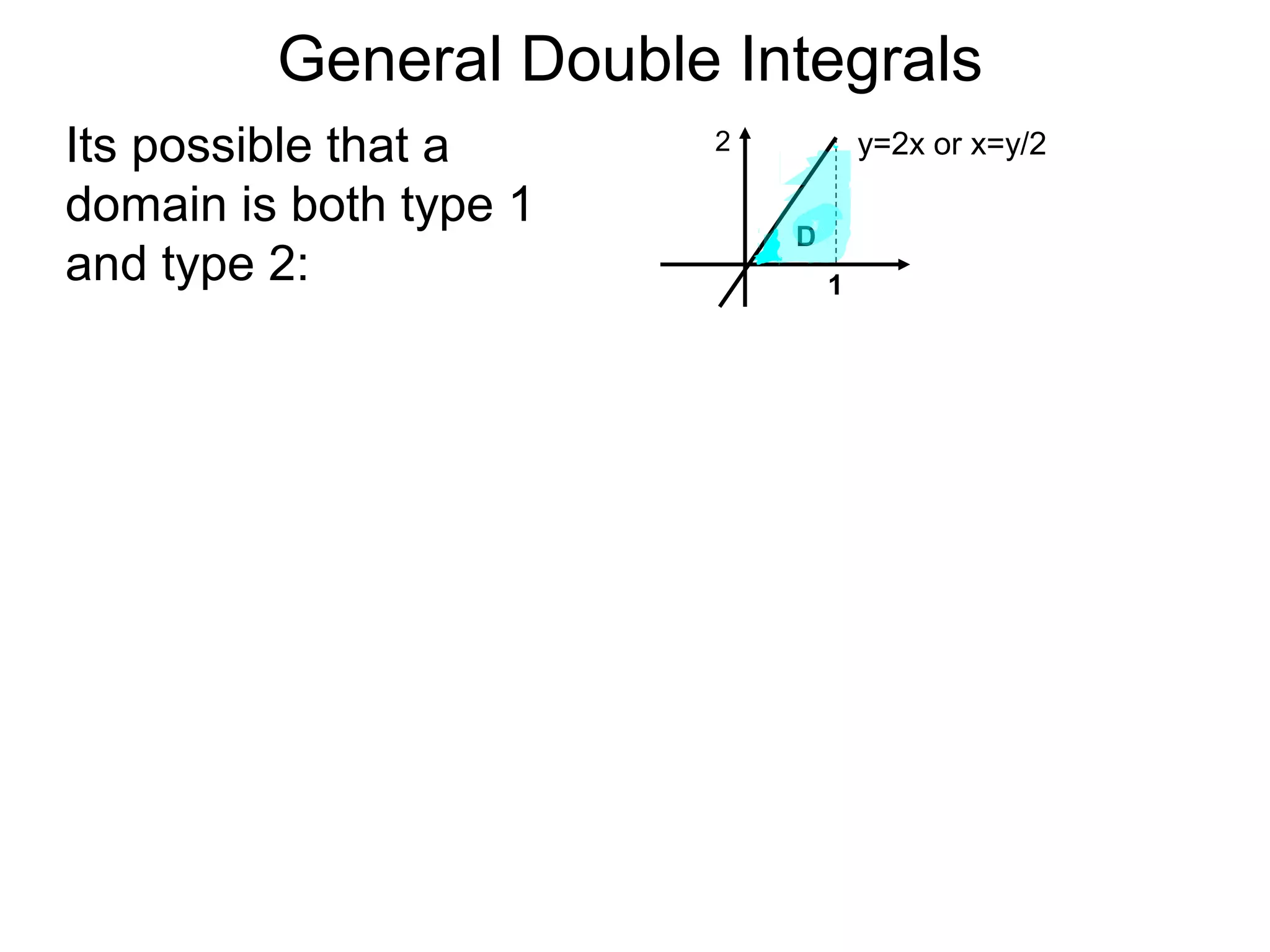
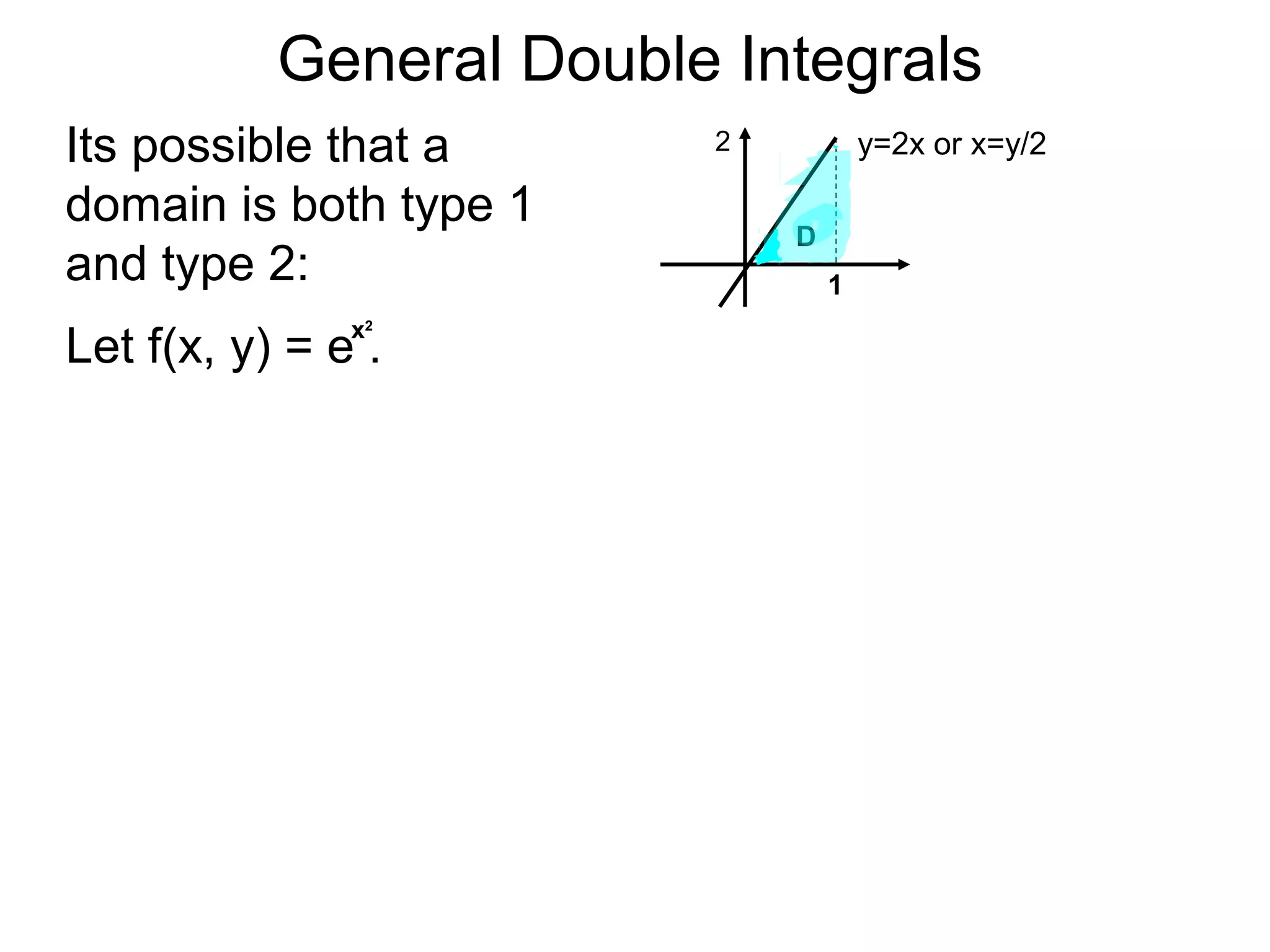
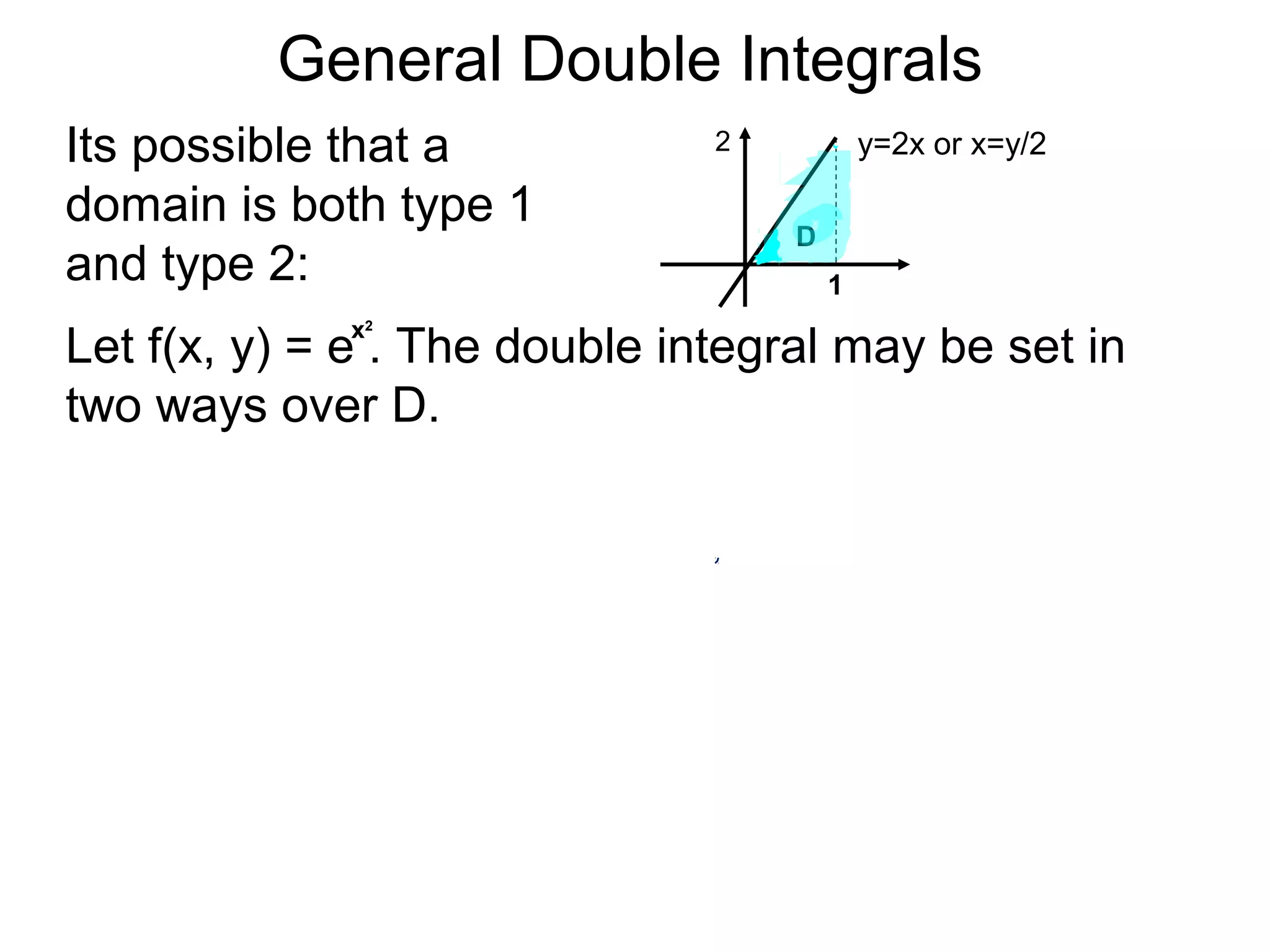
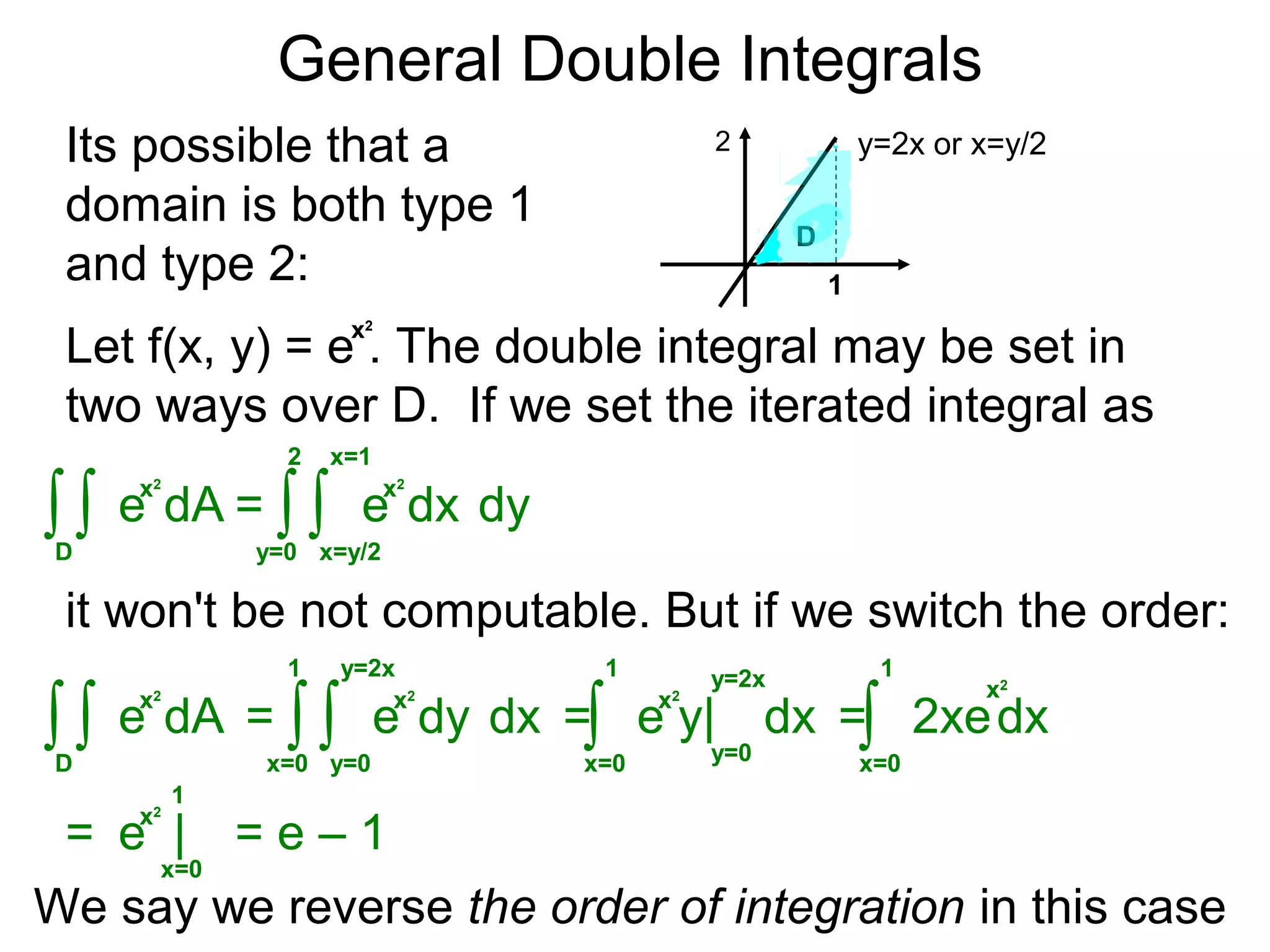
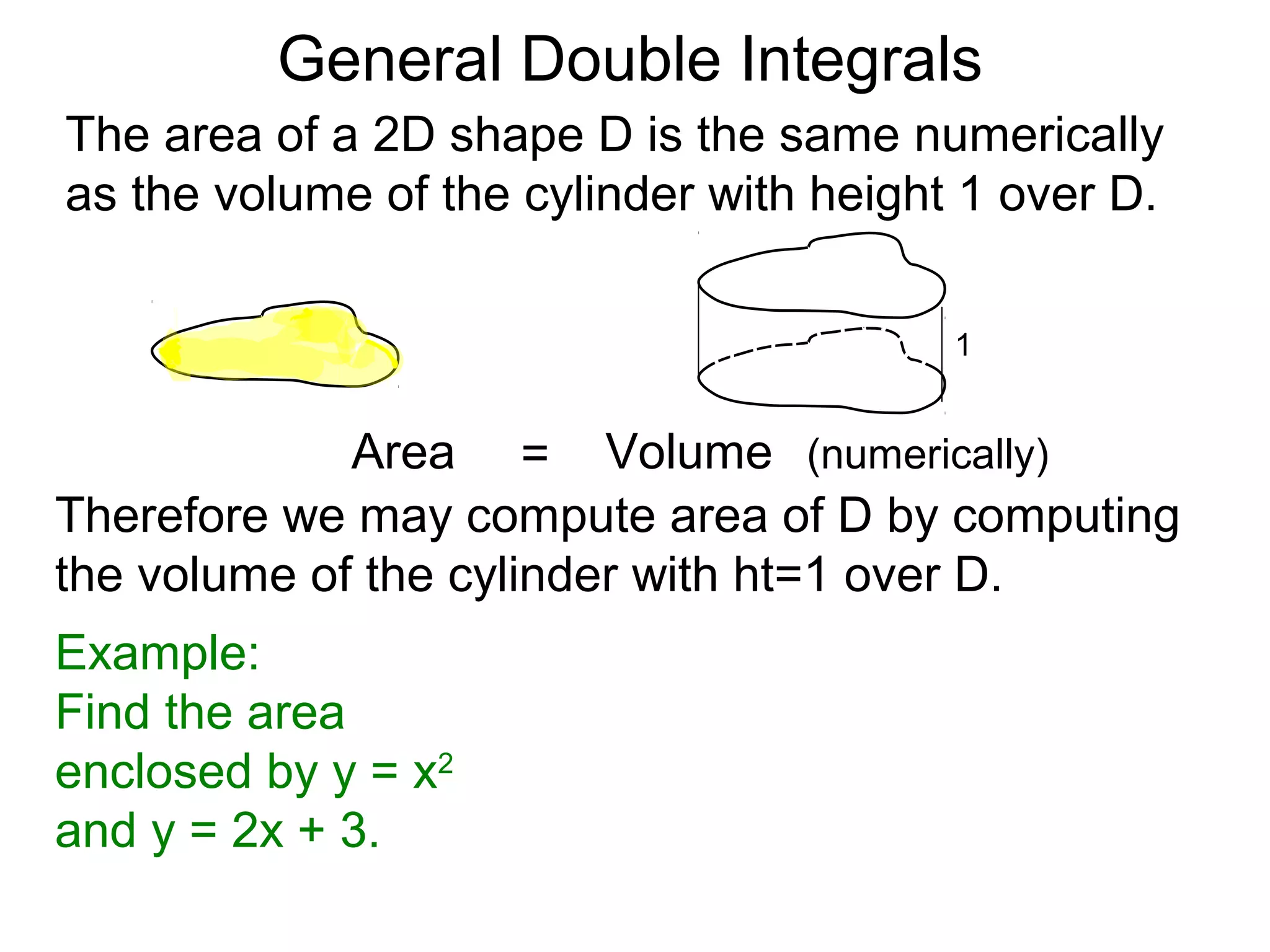
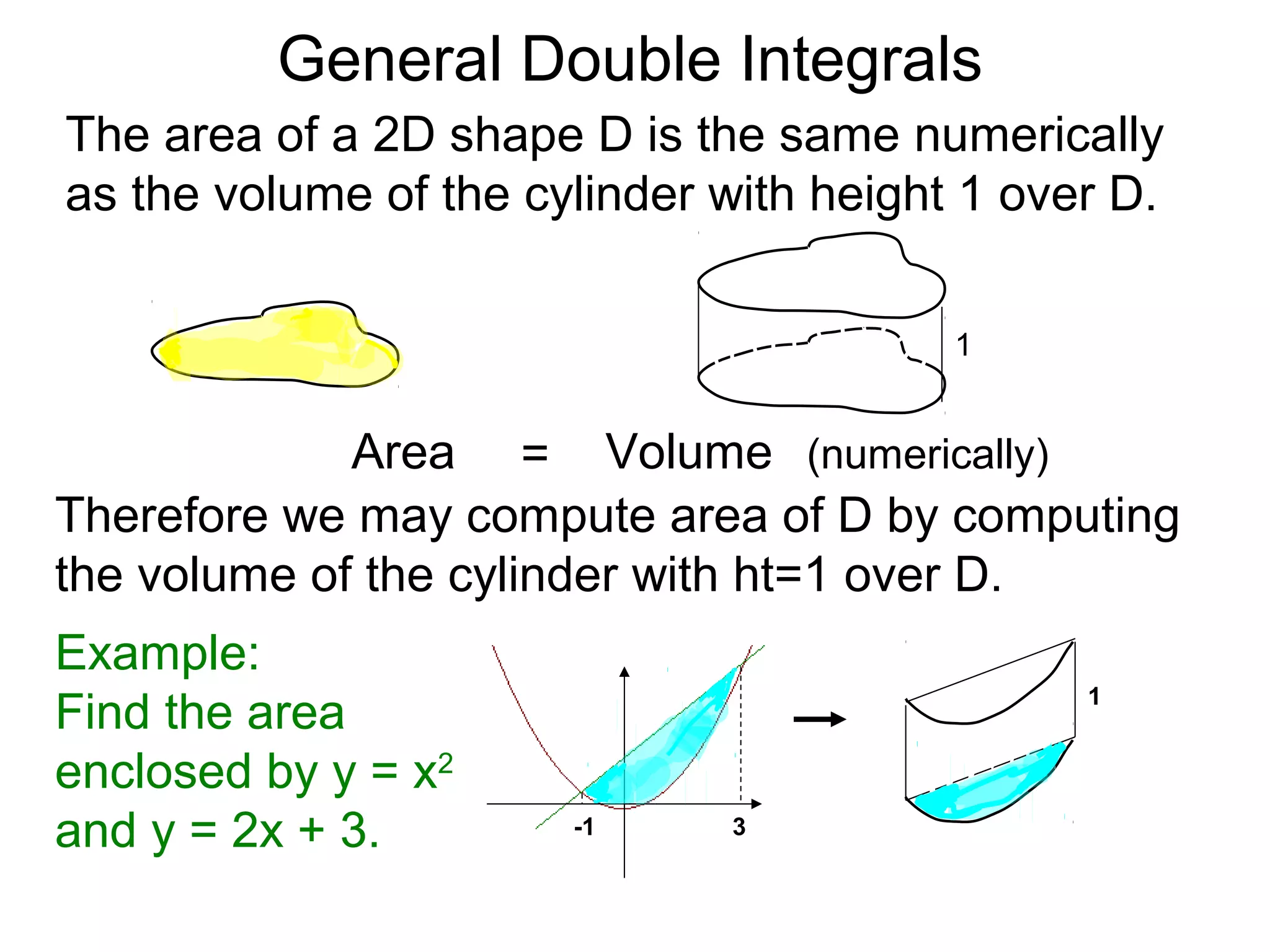
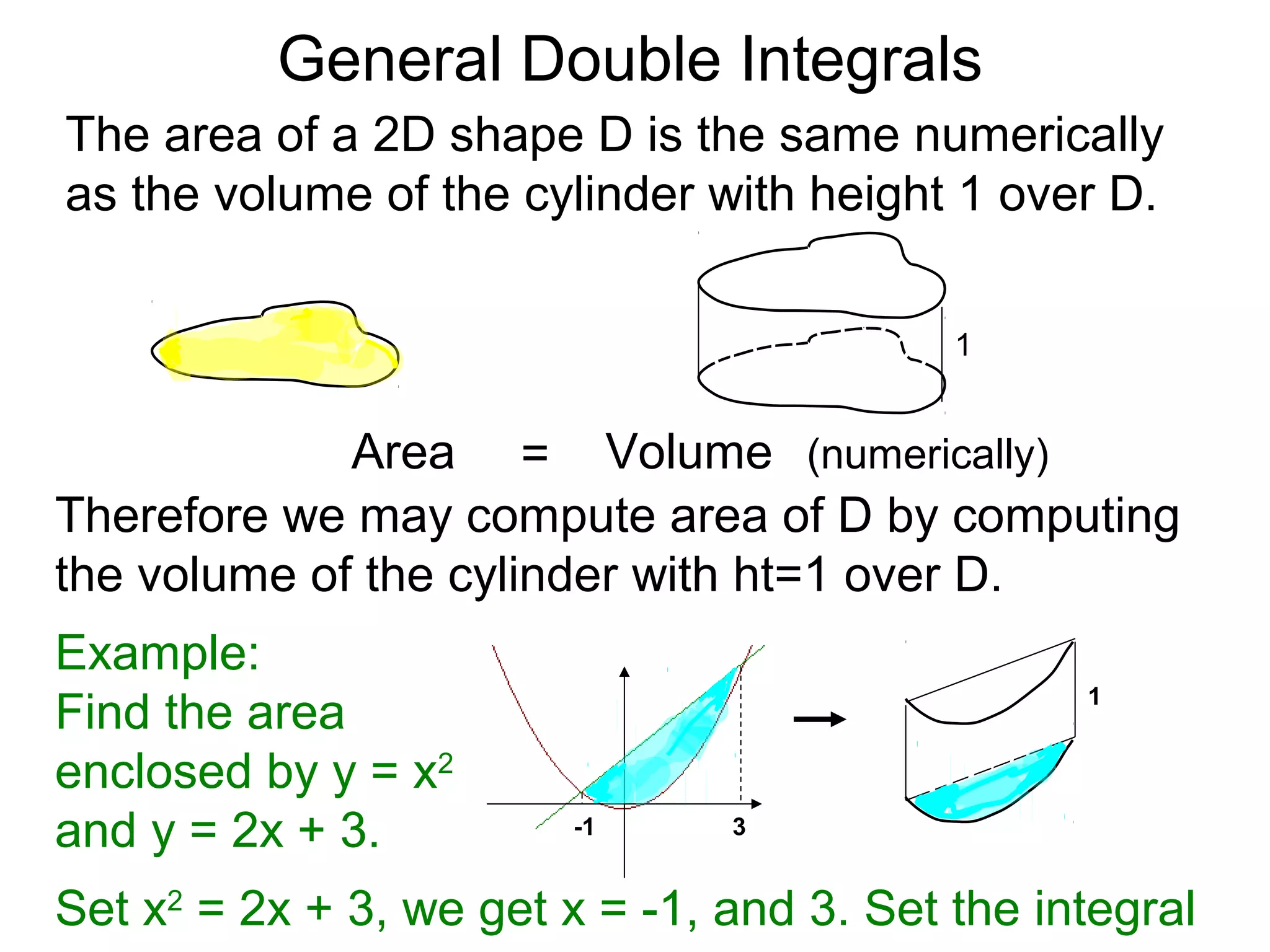
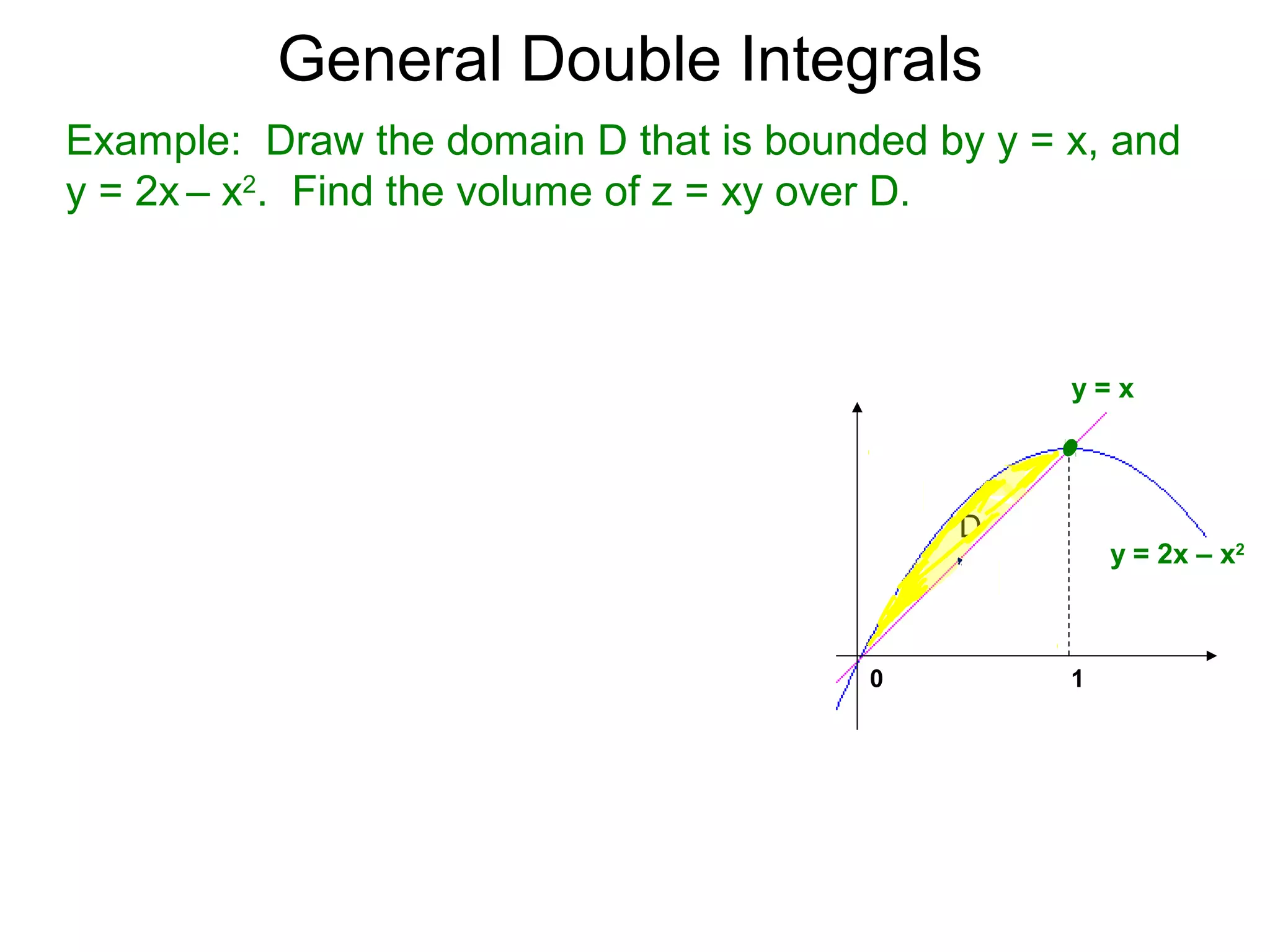
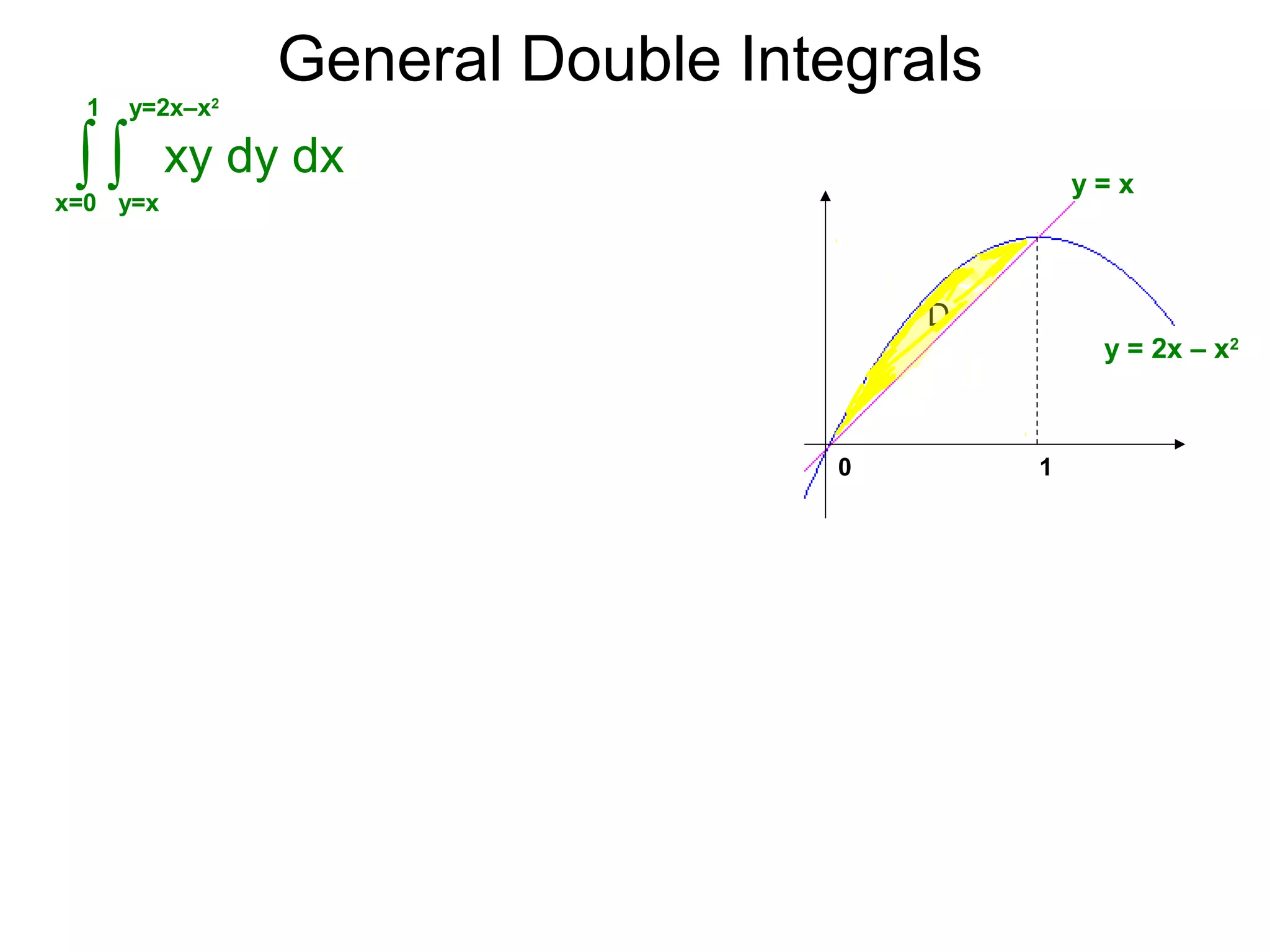
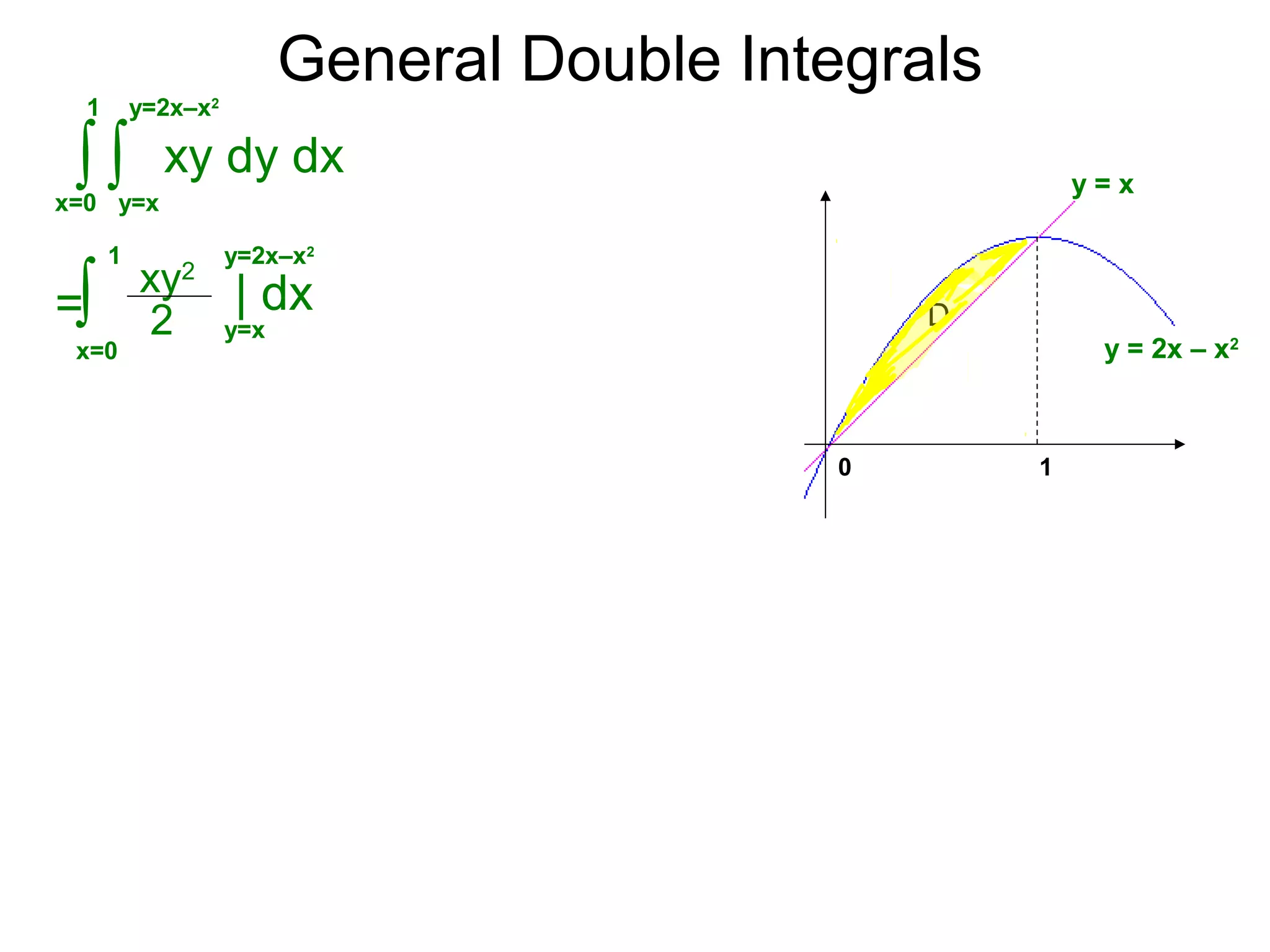
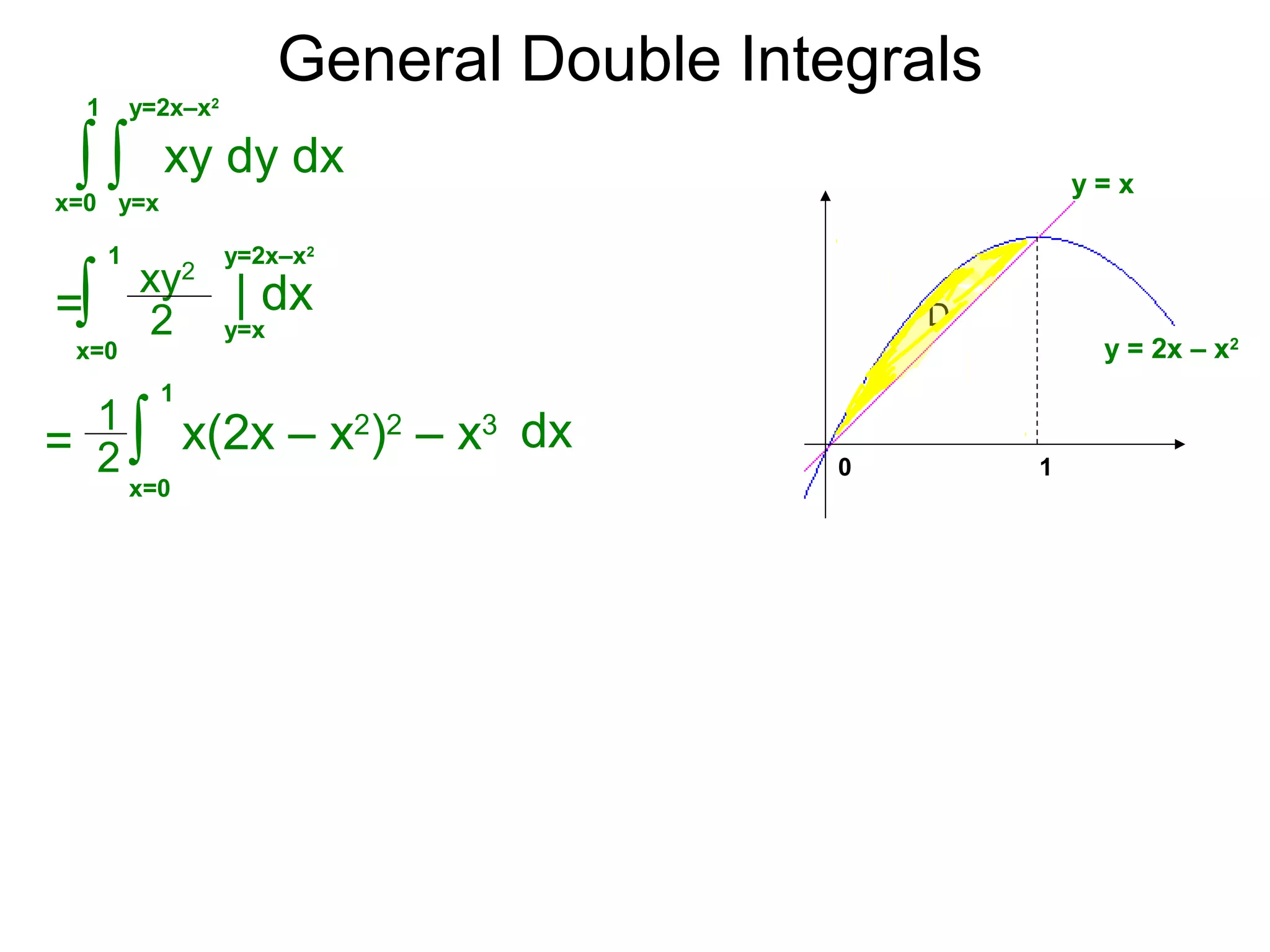
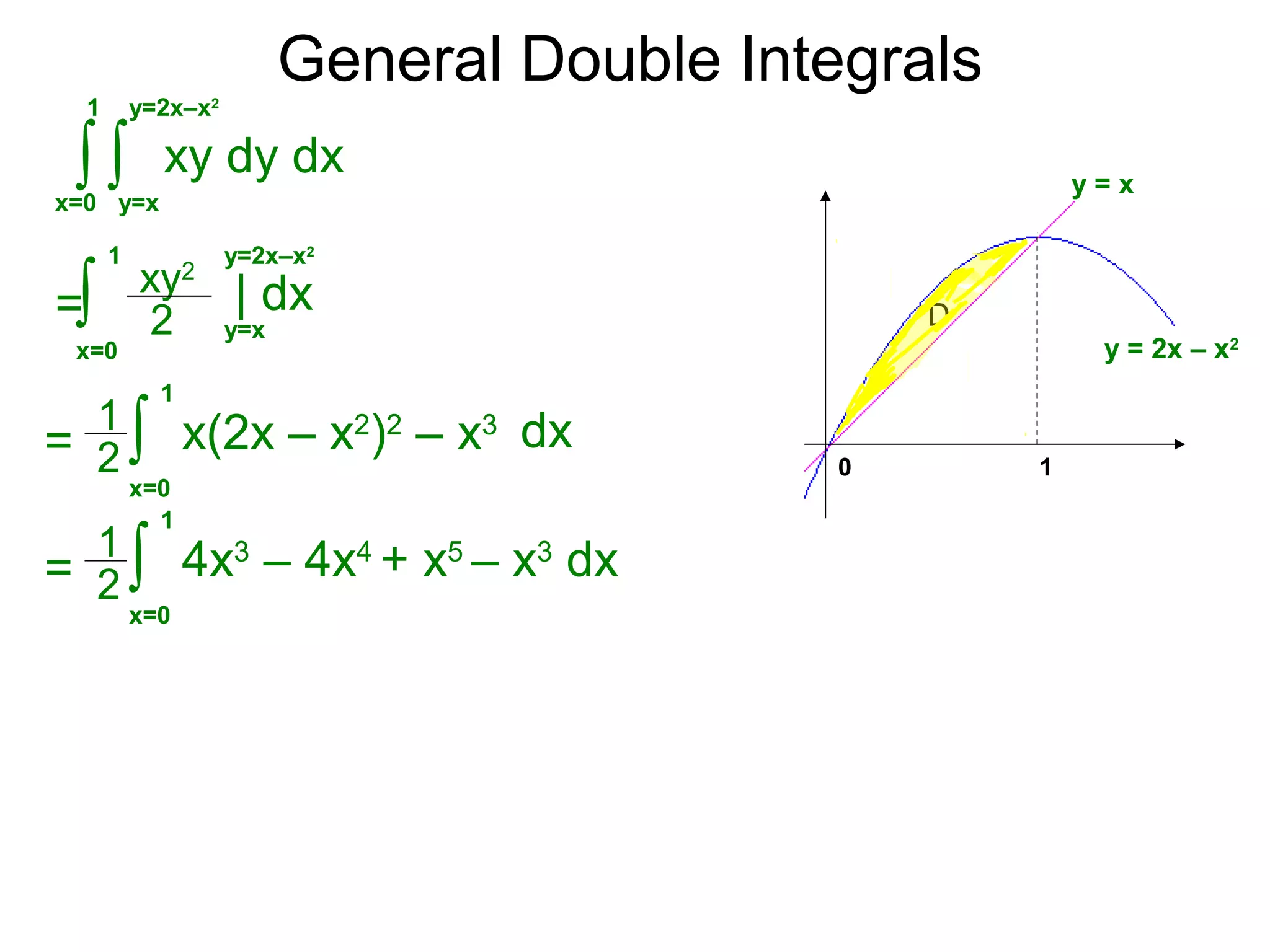
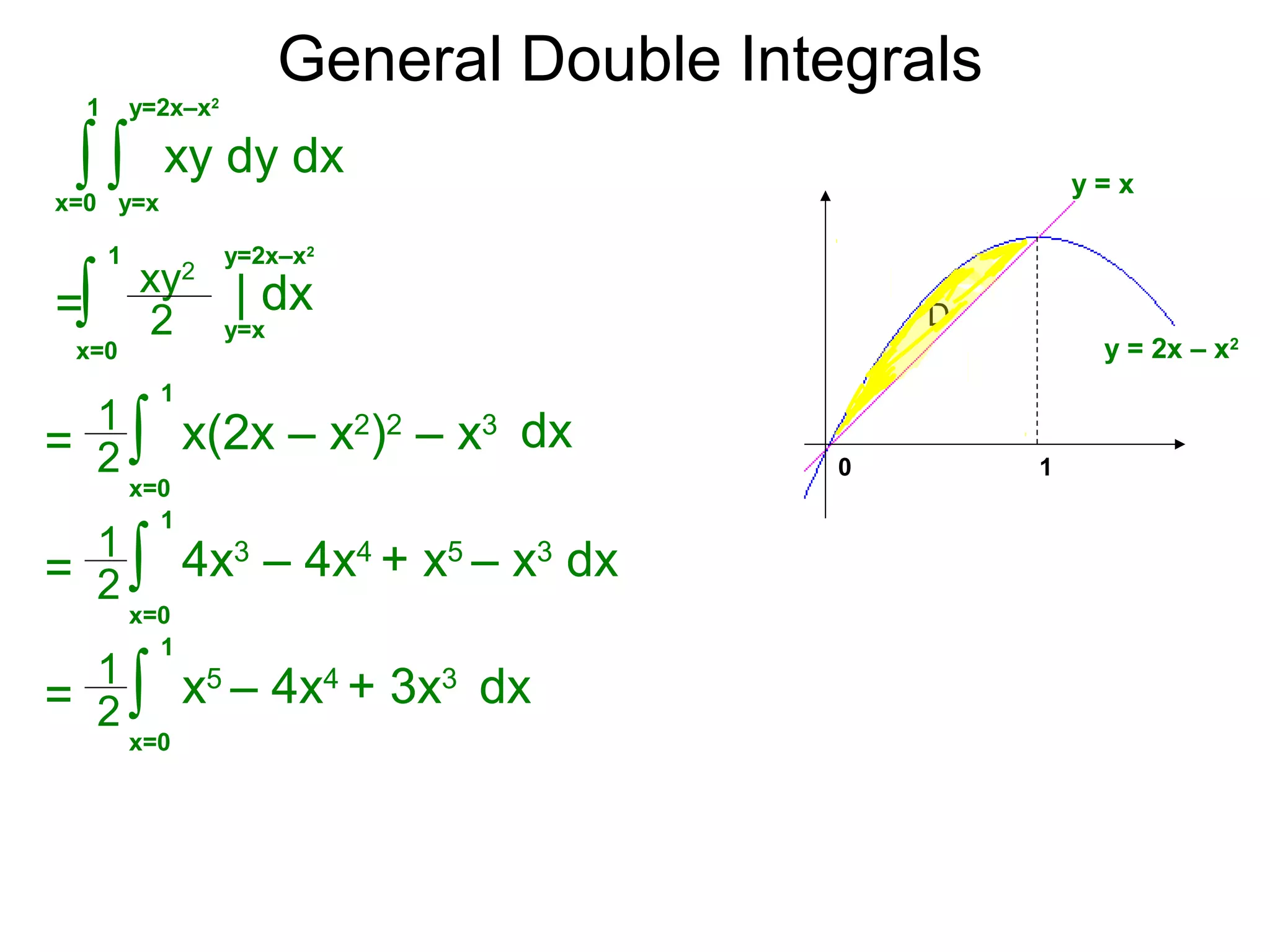
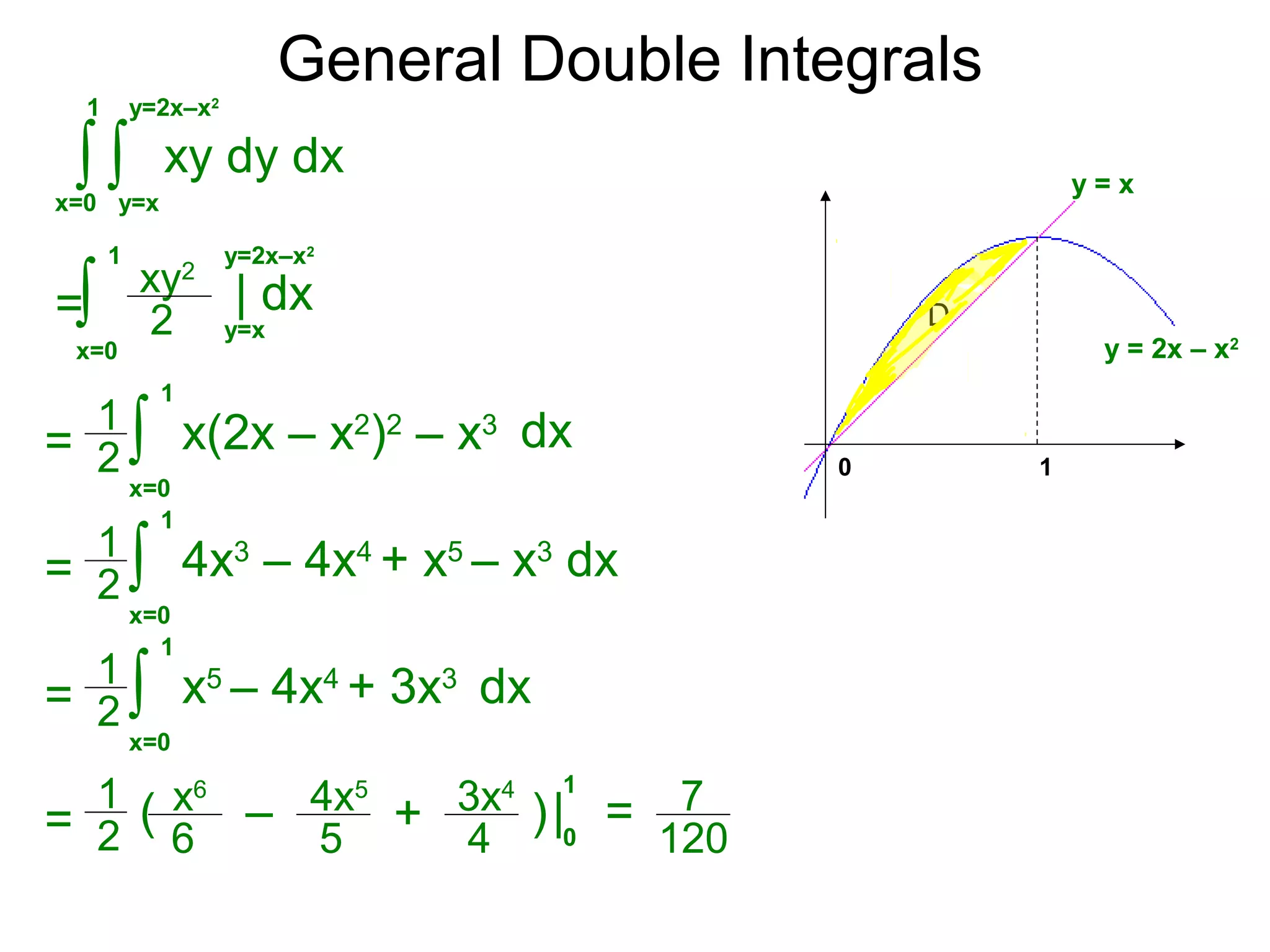
The document defines two types of nonrectangular domains for double integrals. Type 1 is bounded by continuous functions y=f(x) and y=g(x) with a < x < b. Type 2 is bounded by continuous functions x=f(y) and x=g(y) with c < y < d. It provides an example of evaluating a double integral over a Type 1 domain bounded by y=x and y=2x-x^2, finding the volume over the domain to be 120/7. It also discusses describing the domains and the order of integration depends on the type of domain.

1. General Double Integrals

2. General Double Integrals
We will define double integrals over two types of
nonrectangular domains:

3. General Double Integrals
We will define double integrals over two types of
nonrectangular domains:
Type1: A domain that is bounded
up and down by continuous
functions y=f(x) and y=g(x)
where f(x) > g(x) with a < x < b.

4. General Double Integrals
We will define double integrals over two types of
nonrectangular domains:
Type1: A domain that is bounded
up and down by continuous
functions y=f(x) and y=g(x)
where f(x) > g(x) with a < x < b. a b
Type1
y=f(x)
y=g(x)

5. General Double Integrals
We will define double integrals over two types of
nonrectangular domains:
Type1: A domain that is bounded
up and down by continuous
functions y=f(x) and y=g(x)
where f(x) > g(x) with a < x < b. a b
Type1
y=f(x)
y=g(x)
D = {a < x < b, g(x) < y < f(x)}

6. General Double Integrals
We will define double integrals over two types of
nonrectangular domains:
Type1: A domain that is bounded
up and down by continuous
functions y=f(x) and y=g(x)
where f(x) > g(x) with a < x < b.
Type2: A domain that is bounded
left and right by continuous
functions x= f(y) and x=g(y)
where f(y) > g(y) with c < y < d.
a b
Type1
y=f(x)
y=g(x)
D = {a < x < b, g(x) < y < f(x)}

7. General Double Integrals
We will define double integrals over two types of
nonrectangular domains:
Type1: A domain that is bounded
up and down by continuous
functions y=f(x) and y=g(x)
where f(x) > g(x) with a < x < b.
Type2: A domain that is bounded
left and right by continuous
functions x= f(y) and x=g(y)
where f(y) > g(y) with c < y < d.
a b
x=f(y)x=g(y)
d
c
Type1
Type2
y=f(x)
y=g(x)
D = {a < x < b, g(x) < y < f(x)}
D = {c < y < d, g(y) < x < f(y)}

8. General Double Integrals
Given a type 1 domain D, a fixed x defines a
vertical cross-section with the y changes from
g(x) to f(x).
a b
y=f(x)
y=g(x)
D (Type1)
x

9. General Double Integrals
Given a type 1 domain D, a fixed x defines a
vertical cross-section with the y changes from
g(x) to f(x).
a b
y=f(x)
y=g(x)
D (Type1)
x
We decribe D as
{(x, y)| a < x < b; g(x) < y < f(x)}.

10. General Double Integrals
Given a type 1 domain D, a fixed x defines a
vertical cross-section with the y changes from
g(x) to f(x).
a b
y=f(x)
y=g(x)
D (Type1)
x
We decribe D as
{(x, y)| a < x < b; g(x) < y < f(x)}.
Example: Describe D as shown
in the figure.
2y + x = 4
0 4
2
x

11. General Double Integrals
Given a type 1 domain D, a fixed x defines a
vertical cross-section with the y changes from
g(x) to f(x).
a b
y=f(x)
y=g(x)
D (Type1)
x
We decribe D as
{(x, y)| a < x < b; g(x) < y < f(x)}.
Example: Describe D as shown
in the figure.
The x runs from 0 to 4. 2y + x = 4
0 4
2
x

12. General Double Integrals
Given a type 1 domain D, a fixed x defines a
vertical cross-section with the y changes from
g(x) to f(x).
a b
y=f(x)
y=g(x)
D (Type1)
x
We decribe D as
{(x, y)| a < x < b; g(x) < y < f(x)}.
Example: Describe D as shown
in the figure.
The x runs from 0 to 4.
For a fixed x, the y-coordinate of
(x, y)'s run from 0 to (4 – x)/2.
2y + x = 4
0 4
2
x

13. General Double Integrals
Given a type 1 domain D, a fixed x defines a
vertical cross-section with the y changes from
g(x) to f(x).
a b
y=f(x)
y=g(x)
D (Type1)
x
We decribe D as
{(x, y)| a < x < b; g(x) < y < f(x)}.
Example: Describe D as shown
in the figure.
The x runs from 0 to 4.
For a fixed x, the y-coordinate of
(x, y)'s run from 0 to (4 – x)/2.
2y + x = 4
0 4
2
So D ={(x, y)| 0 < x < 4; 0 < y < (4 – x)/2}
x

14. General Double Integrals
Given a type 1 domain D, a fixed x defines a
vertical cross-section with the y changes from
g(x) to f(x).
a b
y=f(x)
y=g(x)
D (Type1)
x
We decribe D as
{(x, y)| a < x < b; g(x) < y < f(x)}.
Example: Describe D as shown
in the figure.
The x runs from 0 to 4.
For a fixed x, the y-coordinate of
(x, y)'s run from 0 to (4 – x)/2.
2y + x = 4
0 4
2
So D ={(x, y)| 0 < x < 4; 0 < y < (4 – x)/2}
x

15. General Double Integrals
Theorem: Let z = z(x, y) over the domain
D = {(x, y)| a < x < b; g(x) < y < f(x)}.
a b
y=f(x)
y=g(x)
D (Type1)
x

16. General Double Integrals
Theorem: Let z = z(x, y) over the domain
D = {(x, y)| a < x < b; g(x) < y < f(x)}.
a b
y=f(x)
y=g(x)
D (Type1)
x
Then
∫ f(x, y)dA =∫ ∫
x=a
b
dxD

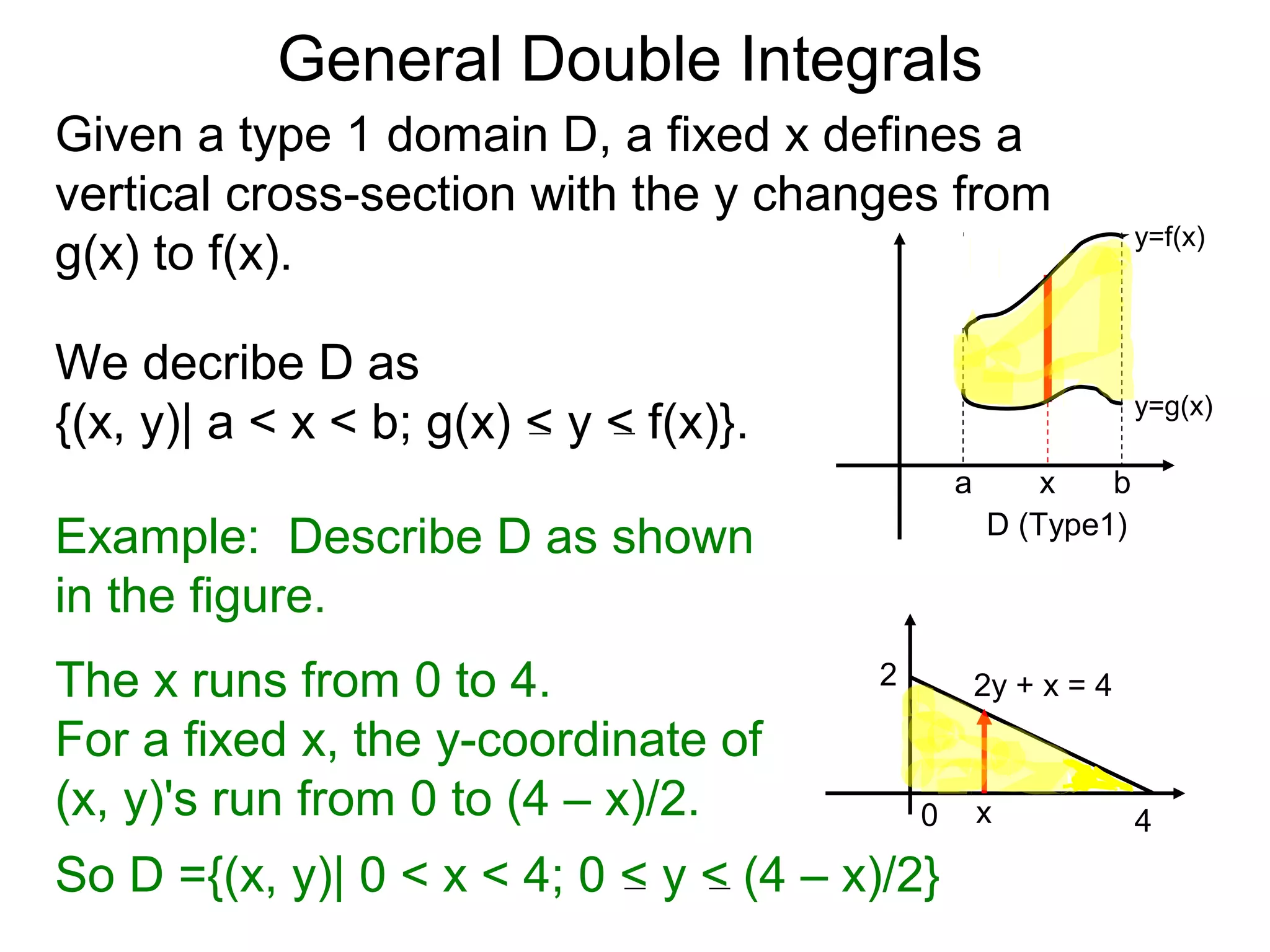
17. General Double Integrals
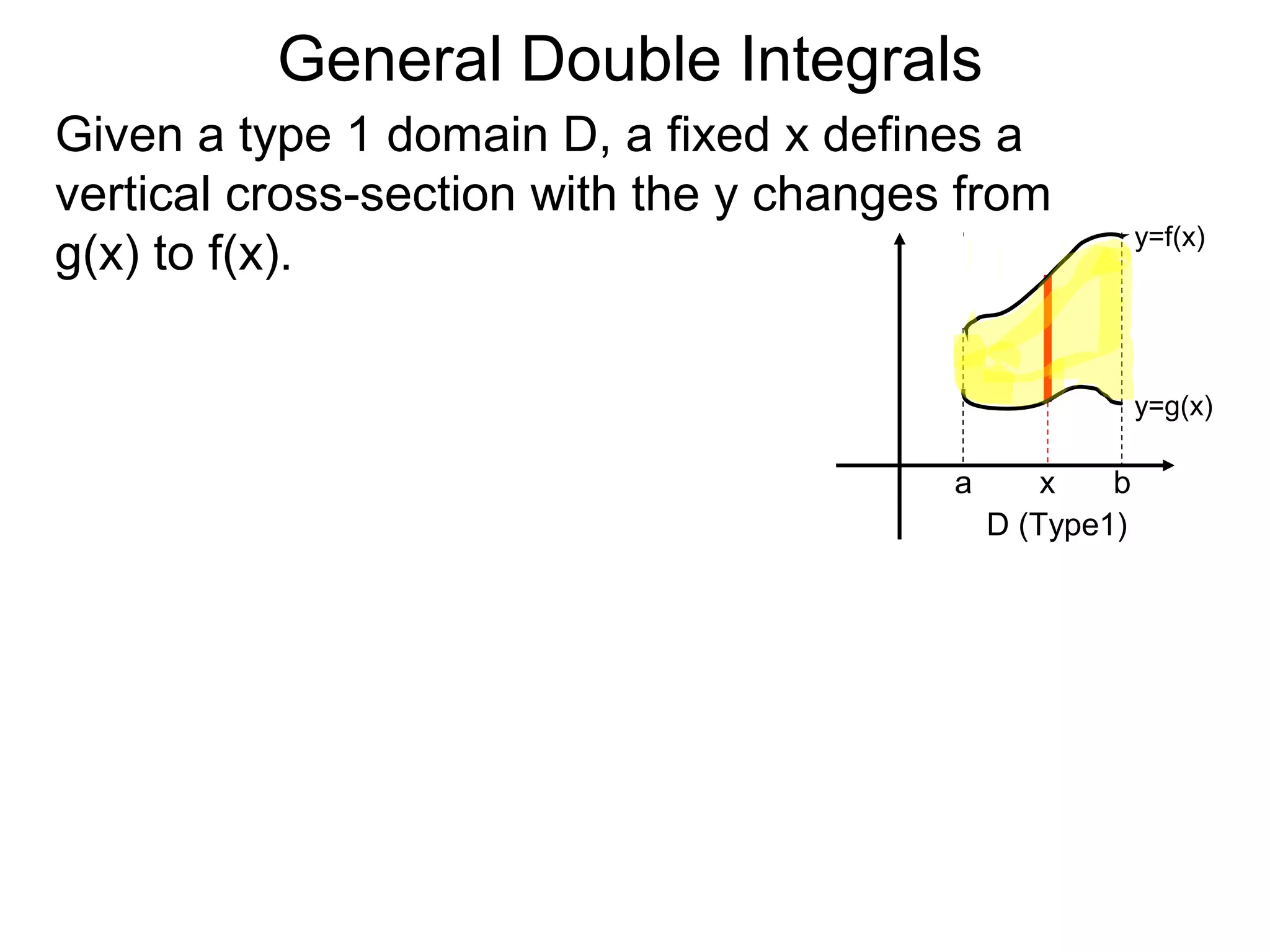
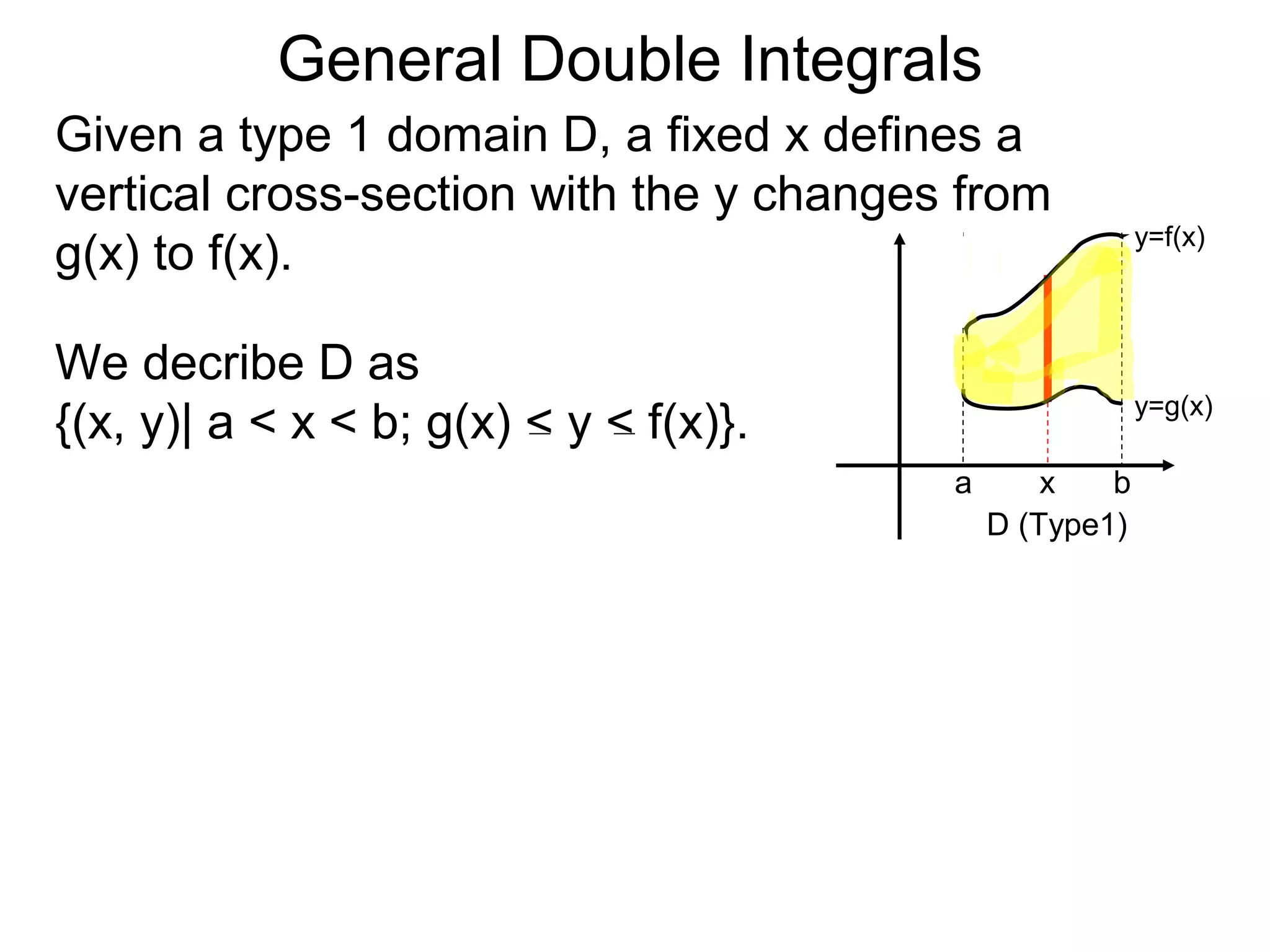
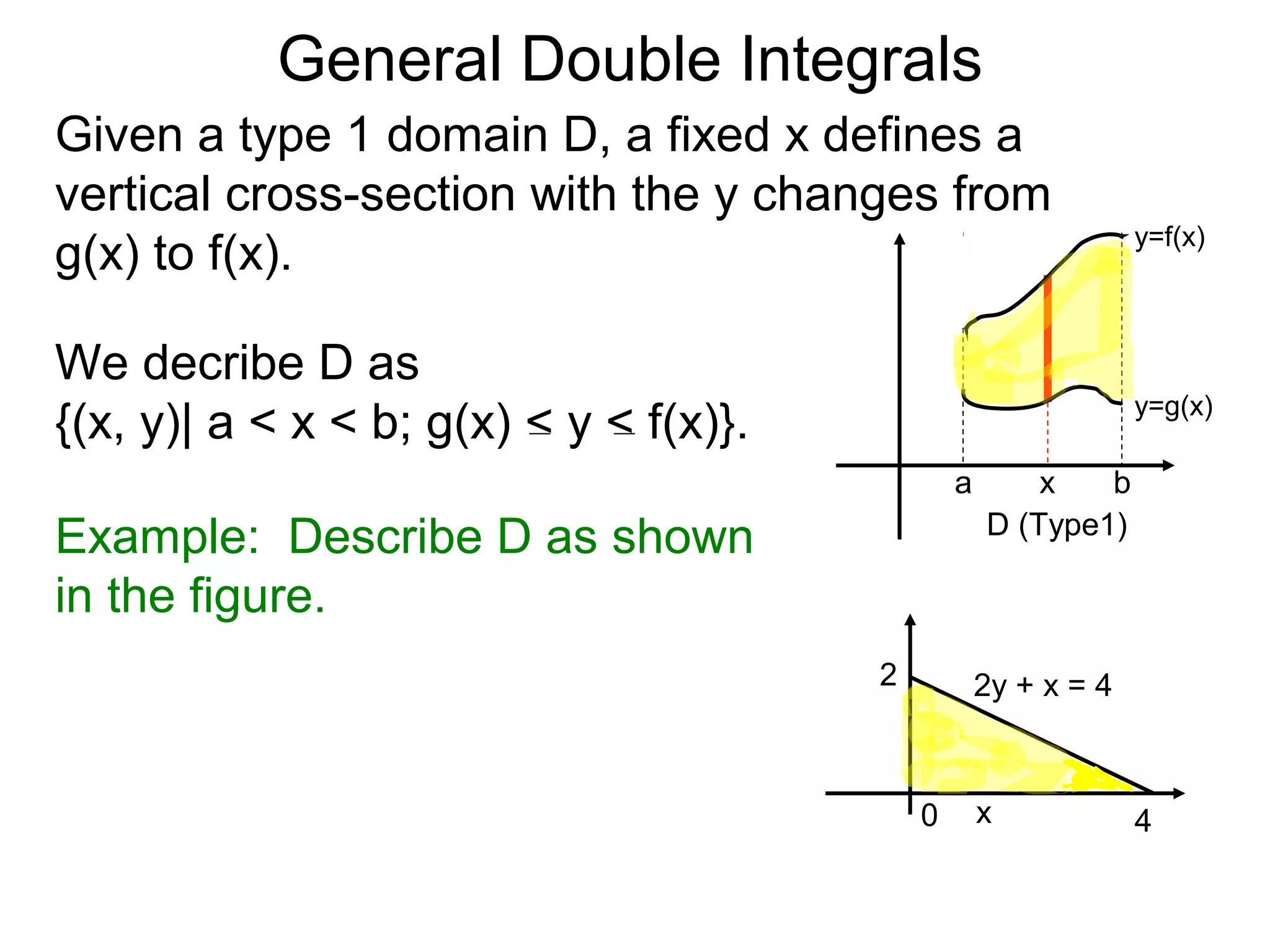
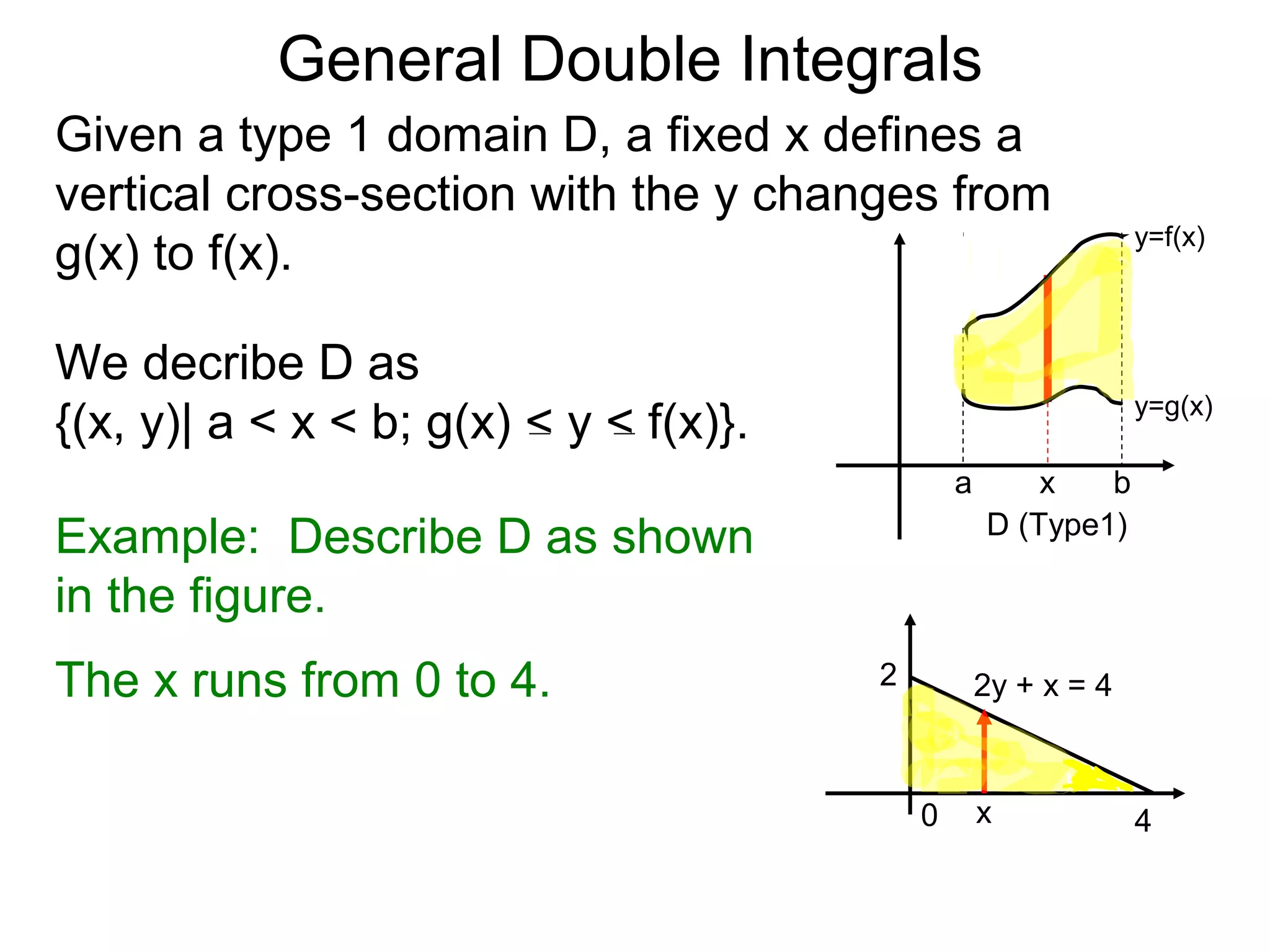
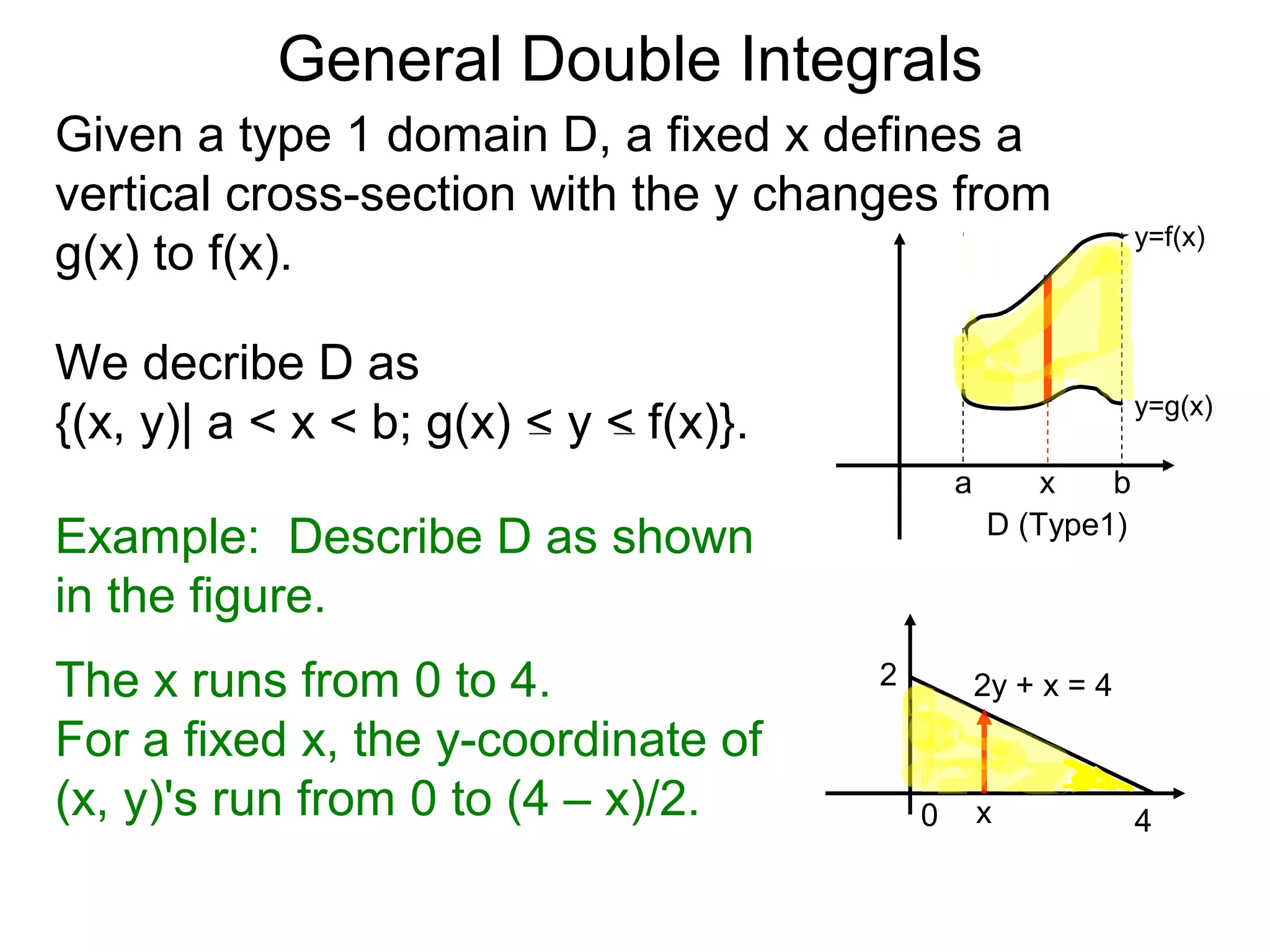
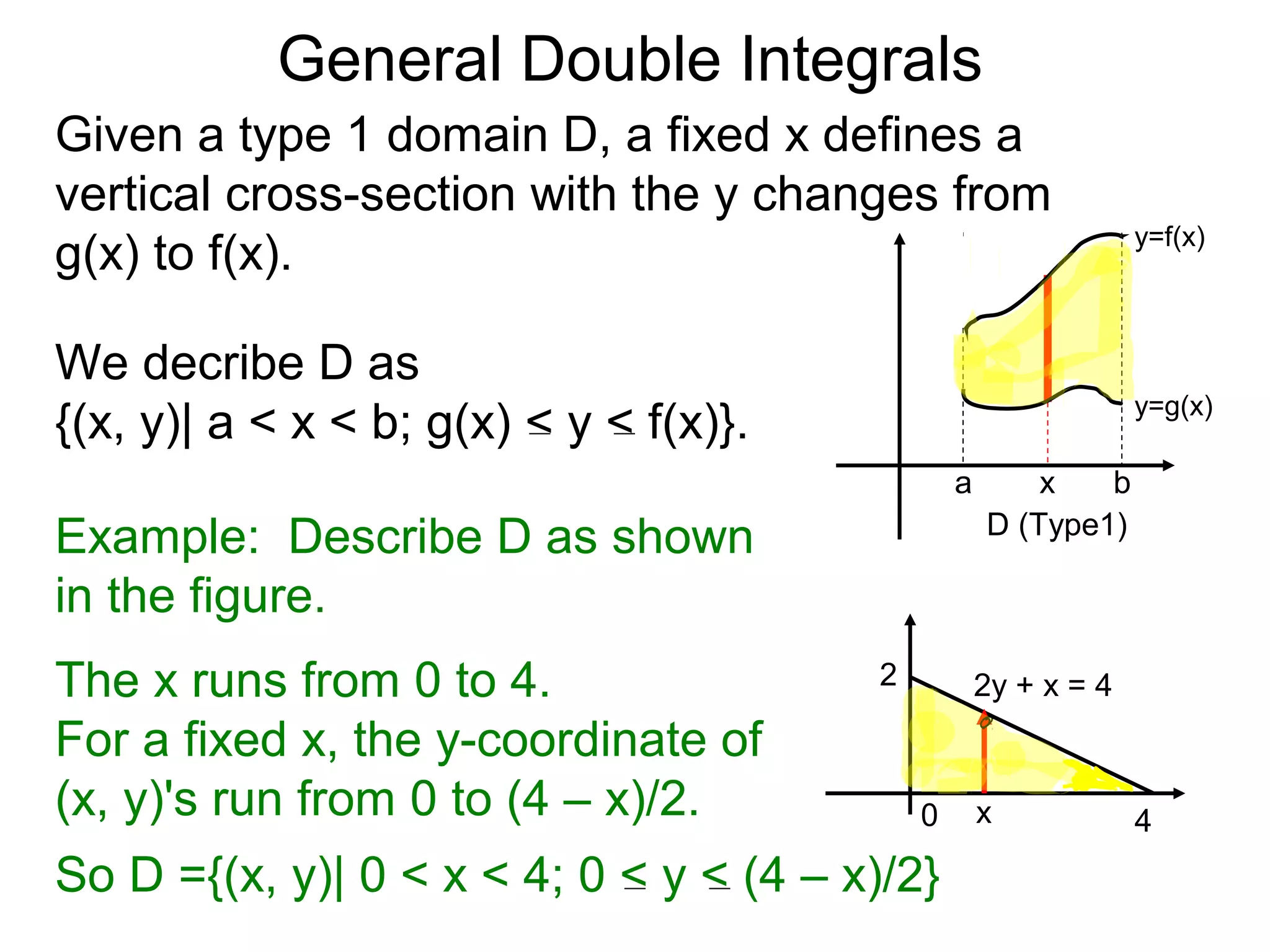
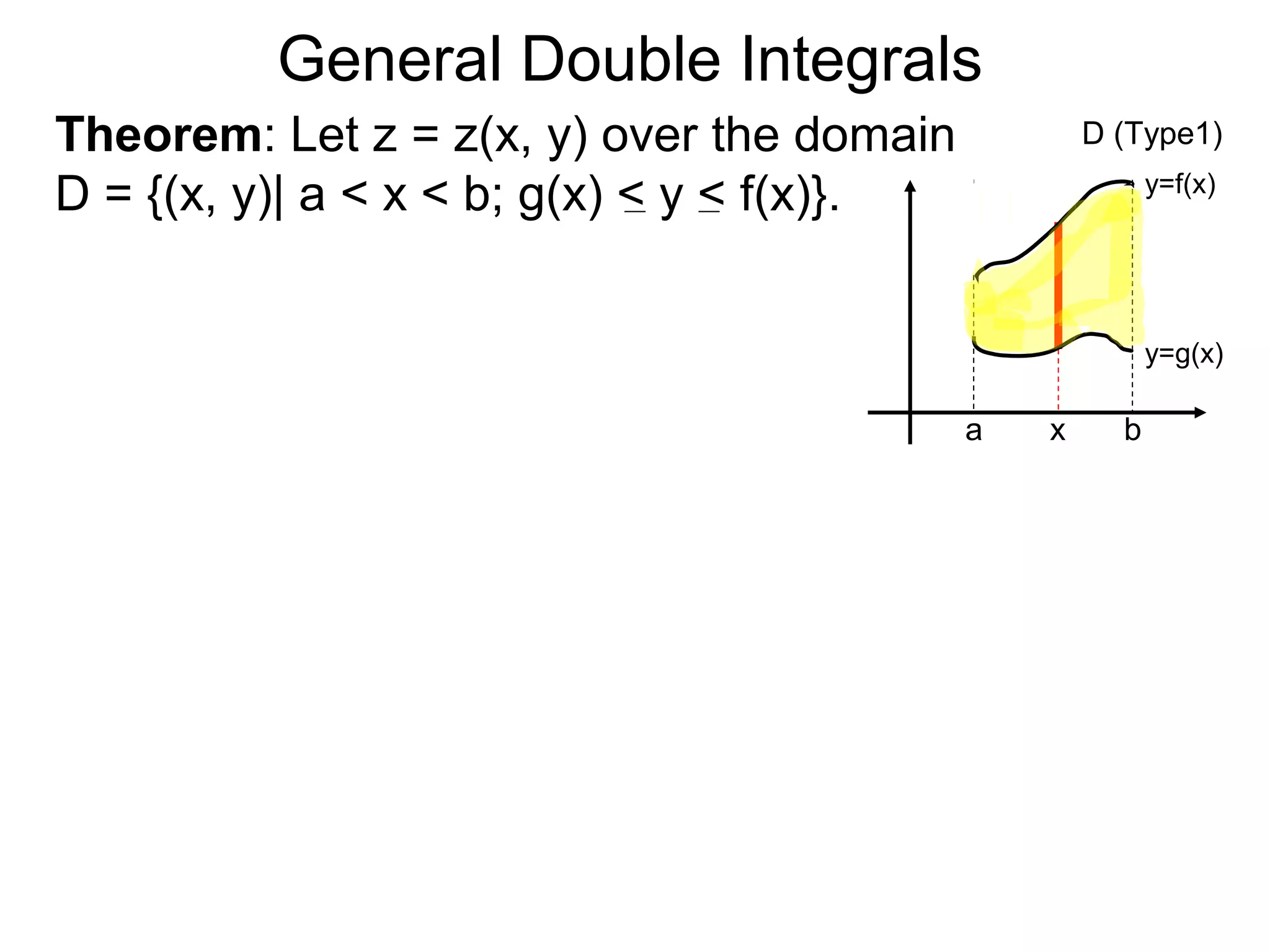
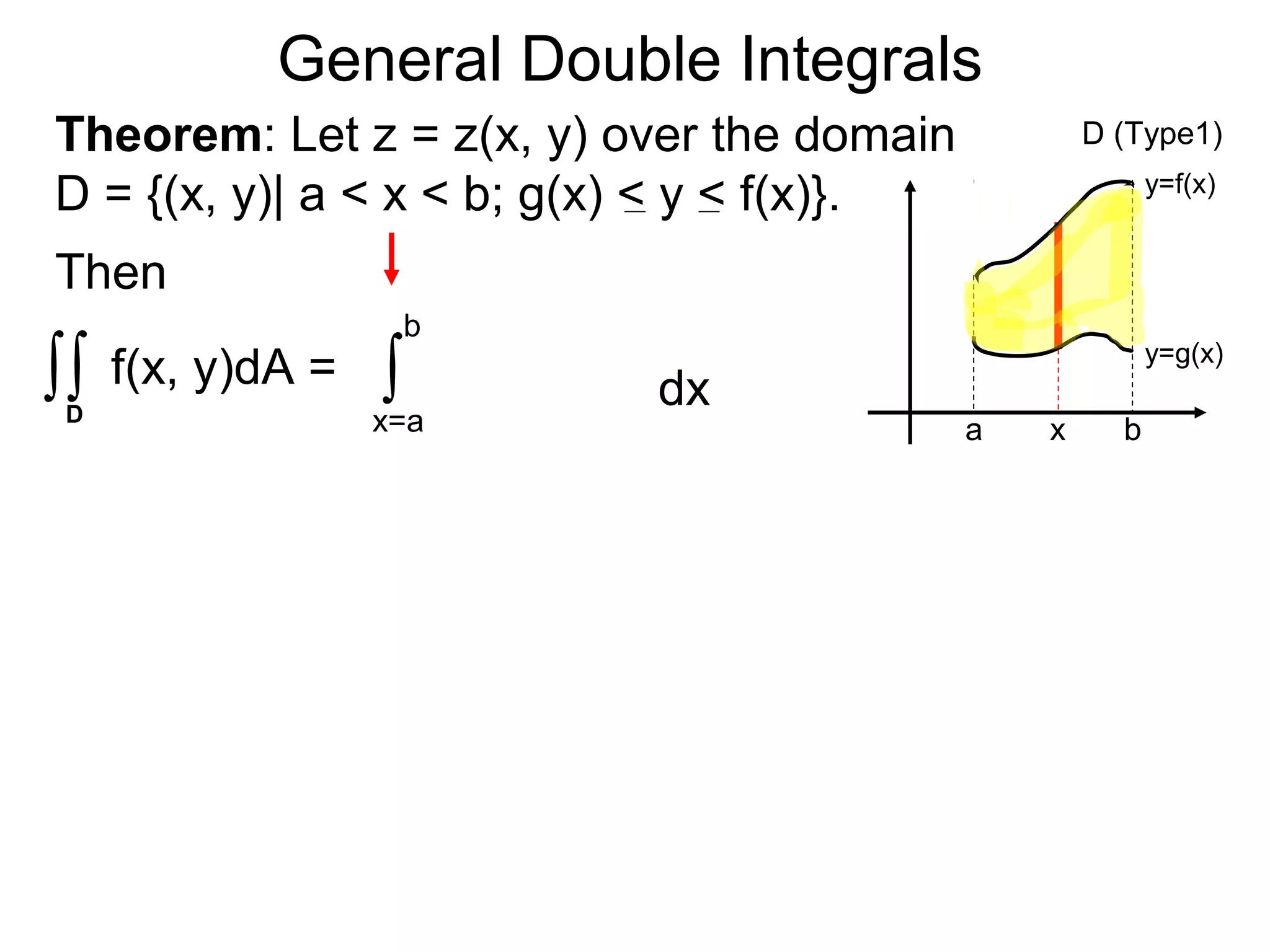
Theorem: Let z = z(x, y) over the domain
D = {(x, y)| a < x < b; g(x) < y < f(x)}.
a b
y=f(x)
y=g(x)
D (Type1)
x
Then
∫ f(x, y)dA =∫ ∫ z(x, y)dy ]dx.
x=a
b
∫y=g(x)
y=f(x)
[
D

18. General Double Integrals
Theorem: Let z = z(x, y) over the domain
D = {(x, y)| a < x < b; g(x) < y < f(x)}.
a b
y=f(x)
y=g(x)
D (Type1)
x
Then
∫ f(x, y)dA =∫ ∫ z(x, y)dy ]dx.
x=a
b
∫y=g(x)
y=f(x)
[
The important thing here is the order of the
integration. It is set according to the the description
of the domain D.
D

19. General Double Integrals
Theorem: Let z = z(x, y) over the domain
D = {(x, y)| a < x < b; g(x) < y < f(x)}.
a b
y=f(x)
y=g(x)
D (Type1)
x
Then
∫ f(x, y)dA =∫ ∫ z(x, y)dy ]dx.
x=a
b
∫y=g(x)
y=f(x)
[
The important thing here is the order of the
integration. It is set according to the the description
of the domain D.
Note that if D is the rectangle [a, b] x [c, d], then
D = {a < x < b; c < y < d} and the double integral is
∫ f(x, y)dA =∫ ∫ z(x, y)dy ]dx.
x=a
b
∫y=c
d
[
D
D

20. General Double Integrals
Example: Draw the domain D that is bounded by y = x, and
y = 2x – x2
. Find the volume of z = xy over D.

21. General Double Integrals
Example: Draw the domain D that is bounded by y = x, and
y = 2x – x2
. Find the volume of z = xy over D.
0 1
D
y = x
y = 2x – x2

22. General Double Integrals
Example: Draw the domain D that is bounded by y = x, and
y = 2x – x2
. Find the volume of z = xy over D.
To solve for intersection, set x = 2x – x2
and get two solutions x = 0, and 1.
0 1
D
y = x
y = 2x – x2

23. General Double Integrals
Example: Draw the domain D that is bounded by y = x, and
y = 2x – x2
. Find the volume of z = xy over D.
So D is bounded above by f(x) = 2x – x2
below by g(x) =x, from x = 0 to x = 1.
To solve for intersection, set x = 2x – x2
and get two solutions x = 0, and 1.
0 1
D
y = x
y = 2x – x2

24. General Double Integrals
Example: Draw the domain D that is bounded by y = x, and
y = 2x – x2
. Find the volume of z = xy over D.
So D is bounded above by f(x) = 2x – x2
below by g(x) =x, from x = 0 to x = 1.
To solve for intersection, set x = 2x – x2
and get two solutions x = 0, and 1.
0 1
D
y = 2x – x2
y = x
So D ={(x, y)| 0 < x < 1; x < y < 2x – x2
}

25. General Double Integrals
Example: Draw the domain D that is bounded by y = x, and
y = 2x – x2
. Find the volume of z = xy over D.
So D is bounded above by f(x) = 2x – x2
below by g(x) =x, from x = 0 to x = 1.
To solve for intersection, set x = 2x – x2
and get two solutions x = 0, and 1.
0 1
D
y = 2x – x2
y = x
So D ={(x, y)| 0 < x < 1; x < y < 2x – x2
}
Set the iterated integral in the given
order:

26. General Double Integrals
Example: Draw the domain D that is bounded by y = x, and
y = 2x – x2
. Find the volume of z = xy over D.
So D is bounded above by f(x) = 2x – x2
below by g(x) =x, from x = 0 to x = 1.
To solve for intersection, set x = 2x – x2
and get two solutions x = 0, and 1.
xy dy dx∫∫ y=xx=0
1 2x–x2
0 1
D
y = 2x – x2
y = x
So D ={(x, y)| 0 < x < 1; x < y < 2x – x2
}
Set the iterated integral in the given
order:

27. General Double Integrals
xy dy dx∫∫ y=xx=0
1 y=2x–x2
0 1
D
y = x
y = 2x – x2

28. General Double Integrals
=
xy2
∫ y=x
x=0
1
2
| dx
y=2x–x2
0 1
D
y = x
y = 2x – x2
xy dy dx∫∫ y=xx=0
1 y=2x–x2

29. General Double Integrals
=
xy2
∫ y=x
x=0
1
2
| dx
= x(2x – x2
)2
– x3
∫
x=0
1
dx1
2
y=2x–x2
0 1
D
y = x
y = 2x – x2
xy dy dx∫∫ y=xx=0
1 y=2x–x2

30. General Double Integrals
=
xy2
∫ y=x
x=0
1
2
| dx
= x(2x – x2
)2
– x3
∫
x=0
1
dx1
2
= 4x3
– 4x4
+ x5
– x3
dx∫
x=0
1
1
2
y=2x–x2
0 1
D
y = x
y = 2x – x2
xy dy dx∫∫ y=xx=0
1 y=2x–x2

31. General Double Integrals
=
xy2
∫ y=x
x=0
1
2
| dx
= x(2x – x2
)2
– x3
∫
x=0
1
dx1
2
= 4x3
– 4x4
+ x5
– x3
dx∫
x=0
1
1
2
= x5
– 4x4
+ 3x3
dx∫
x=0
1
1
2
y=2x–x2
0 1
D
y = x
y = 2x – x2
xy dy dx∫∫ y=xx=0
1 y=2x–x2

32. General Double Integrals
=
xy2
∫ y=x
x=0
1
2
| dx
= x(2x – x2
)2
– x3
∫
x=0
1
dx1
2
= 4x3
– 4x4
+ x5
– x3
dx∫
x=0
1
1
2
= x5
– 4x4
+ 3x3
dx∫
x=0
1
1
2
=
1
2 6
( x6
+5
4x5
)|
1
0
y=2x–x2
–
4
3x4
0 1
D
=
120
7
y = x
y = 2x – x2
xy dy dx∫∫ y=xx=0
1 y=2x–x2

33. General Double Integrals
Given a type 2 domain D,
x=f(y)x=g(y)
d
c
D Type2
x

34. General Double Integrals
Given a type 2 domain D, a fixed y defines a
vertical cross-section with the x changes from
g(y) to f(y).
x=f(y)x=g(y)
d
c
D Type2
x
y

35. General Double Integrals
Given a type 2 domain D, a fixed y defines a
vertical cross-section with the x changes from
g(y) to f(y).
We decribe D as
{(x, y)| c < y < d; g(y) < x < f(y)}.
x=f(y)x=g(y)
d
c
D Type2
x
y

36. General Double Integrals
Given a type 2 domain D, a fixed y defines a
vertical cross-section with the x changes from
g(y) to f(y).
We decribe D as
{(x, y)| c < y < d; g(y) < x < f(y)}.
Example: Describe D as shown
in the figure.
2y + x = 4
0 4
2
y
x=f(y)x=g(y)
d
c
D Type2
x
y

37. General Double Integrals
Given a type 2 domain D, a fixed y defines a
vertical cross-section with the x changes from
g(y) to f(y).
We decribe D as
{(x, y)| c < y < d; g(y) < x < f(y)}.
Example: Describe D as shown
in the figure.
The y run from 0 to 2. 2y + x = 4
0 4
2
y
x=f(y)x=g(y)
d
c
D Type2
x
y

38. General Double Integrals
Given a type 2 domain D, a fixed y defines a
vertical cross-section with the x changes from
g(y) to f(y).
We decribe D as
{(x, y)| c < y < d; g(y) < x < f(y)}.
Example: Describe D as shown
in the figure.
The y run from 0 to 2.
For a fixed y, the x-coordinate of
(x, y)'s run from 0 to 4 – 2y.
2y + x = 4
0 4
2
y
x=f(y)x=g(y)
d
c
D Type2
x
y

39. General Double Integrals
Given a type 2 domain D, a fixed y defines a
vertical cross-section with the x changes from
g(y) to f(y).
We decribe D as
{(x, y)| c < y < d; g(y) < x < f(y)}.
Example: Describe D as shown
in the figure.
The y run from 0 to 2.
For a fixed y, the x-coordinate of
(x, y)'s run from 0 to 4 – 2y.
2y + x = 4
0 4
2
So D ={(x, y)| 0 < y < 2; 0 < x < 4 – 2y}
y
x=f(y)x=g(y)
d
c
D Type2
x
y

40. General Double Integrals
Theorem: Let z = z(x, y) over the domain
D = {(x, y)| c < y < d; g(y) < x < f(y)}. x=f(y)x=g(y)
d
c
D Type2
x
y

41. General Double Integrals
Theorem: Let z = z(x, y) over the domain
D = {(x, y)| c < y < d; g(y) < x < f(y)}.
Then
∫ f(x, y)dA =∫ ∫ dy.
y=c
d
D
x=f(y)x=g(y)
d
c
D Type2
x
y

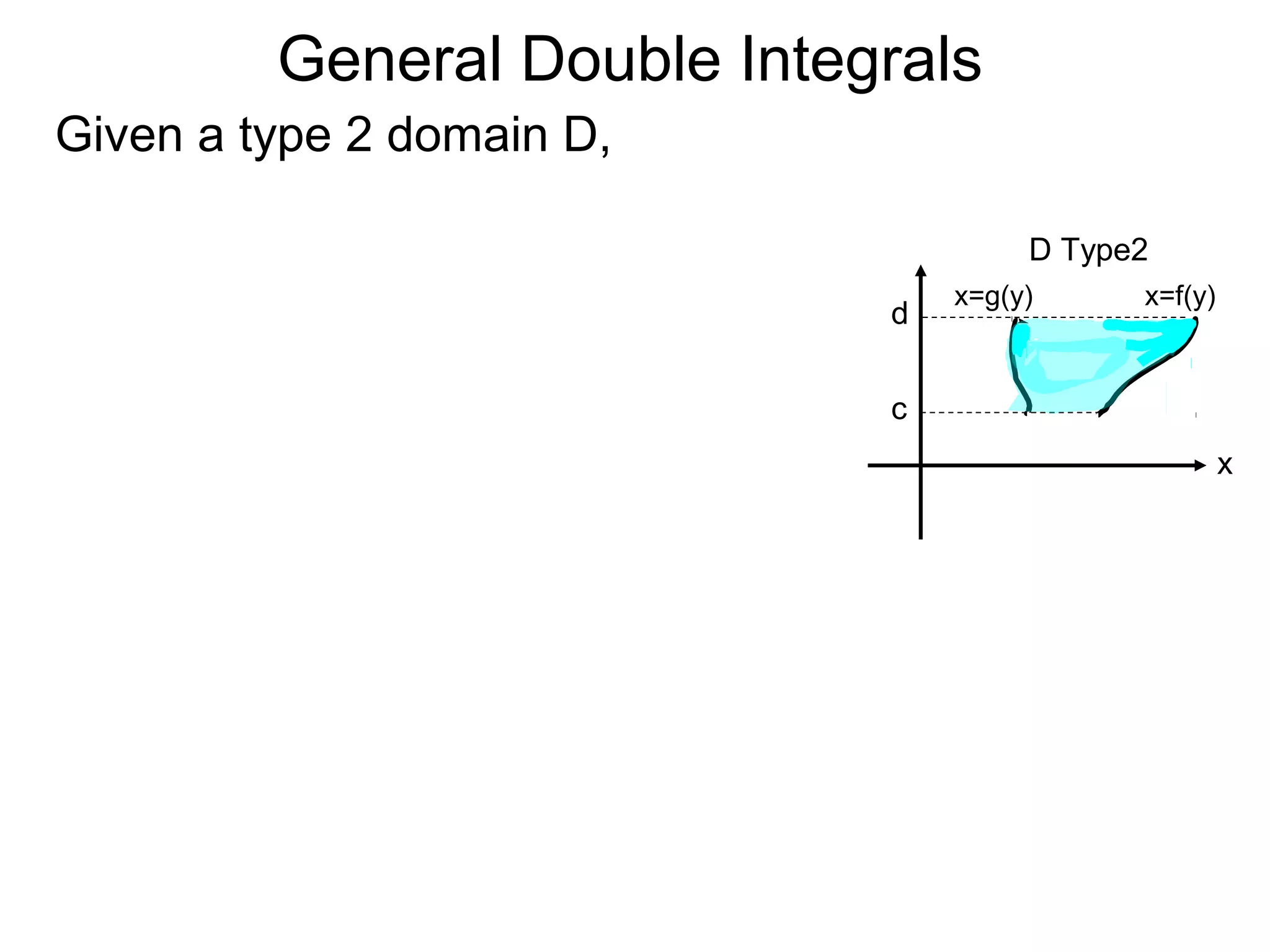
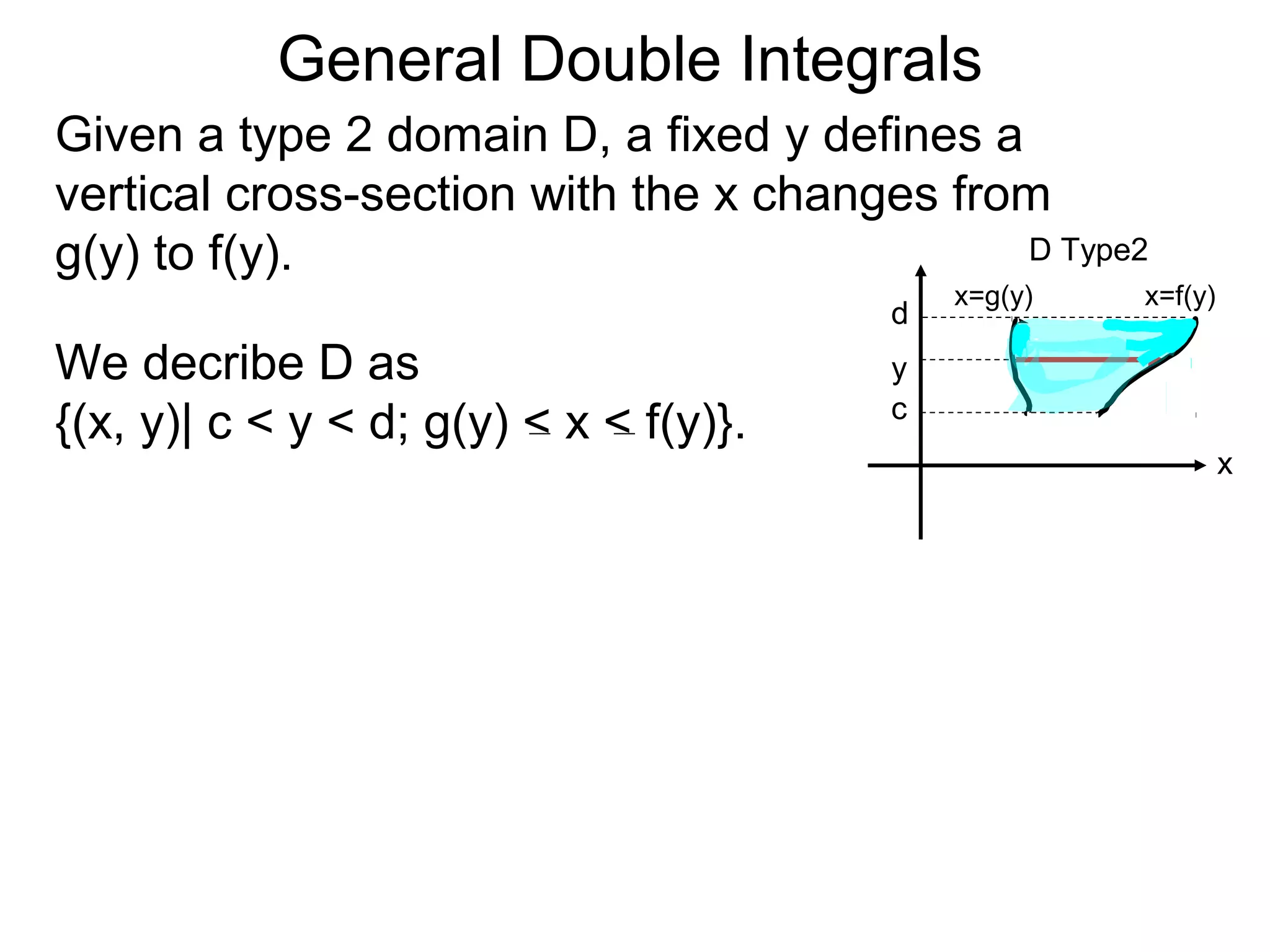
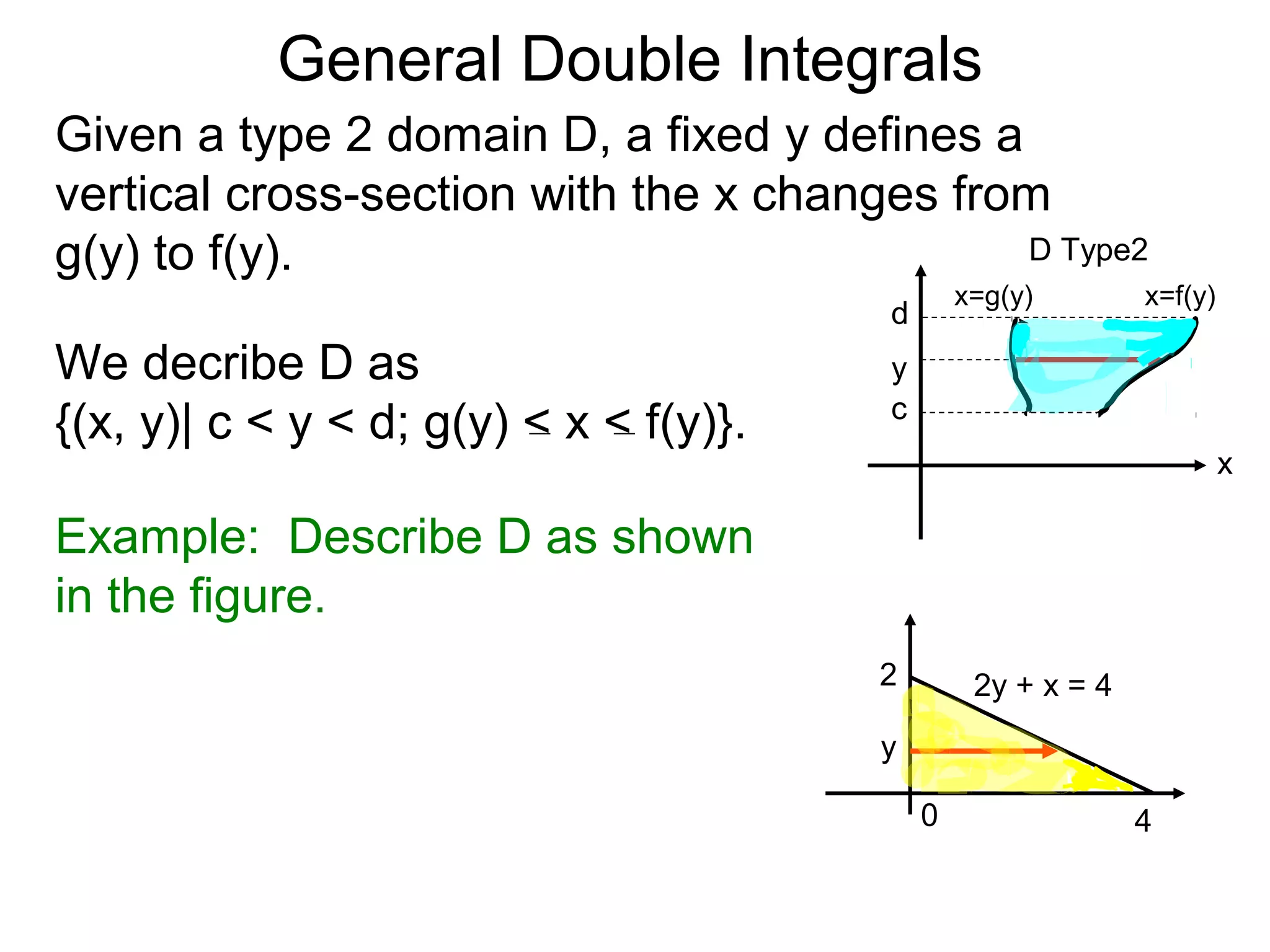
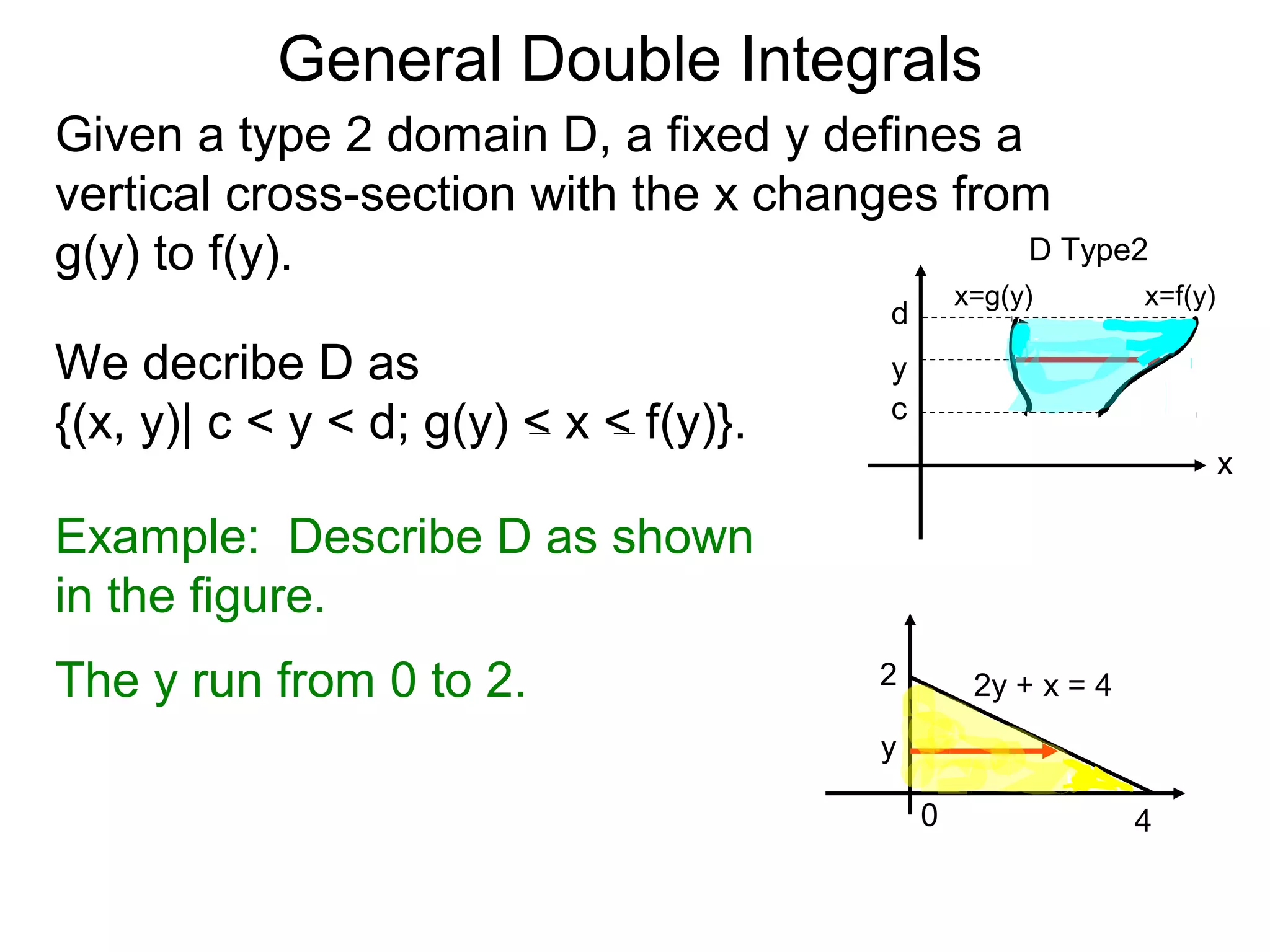
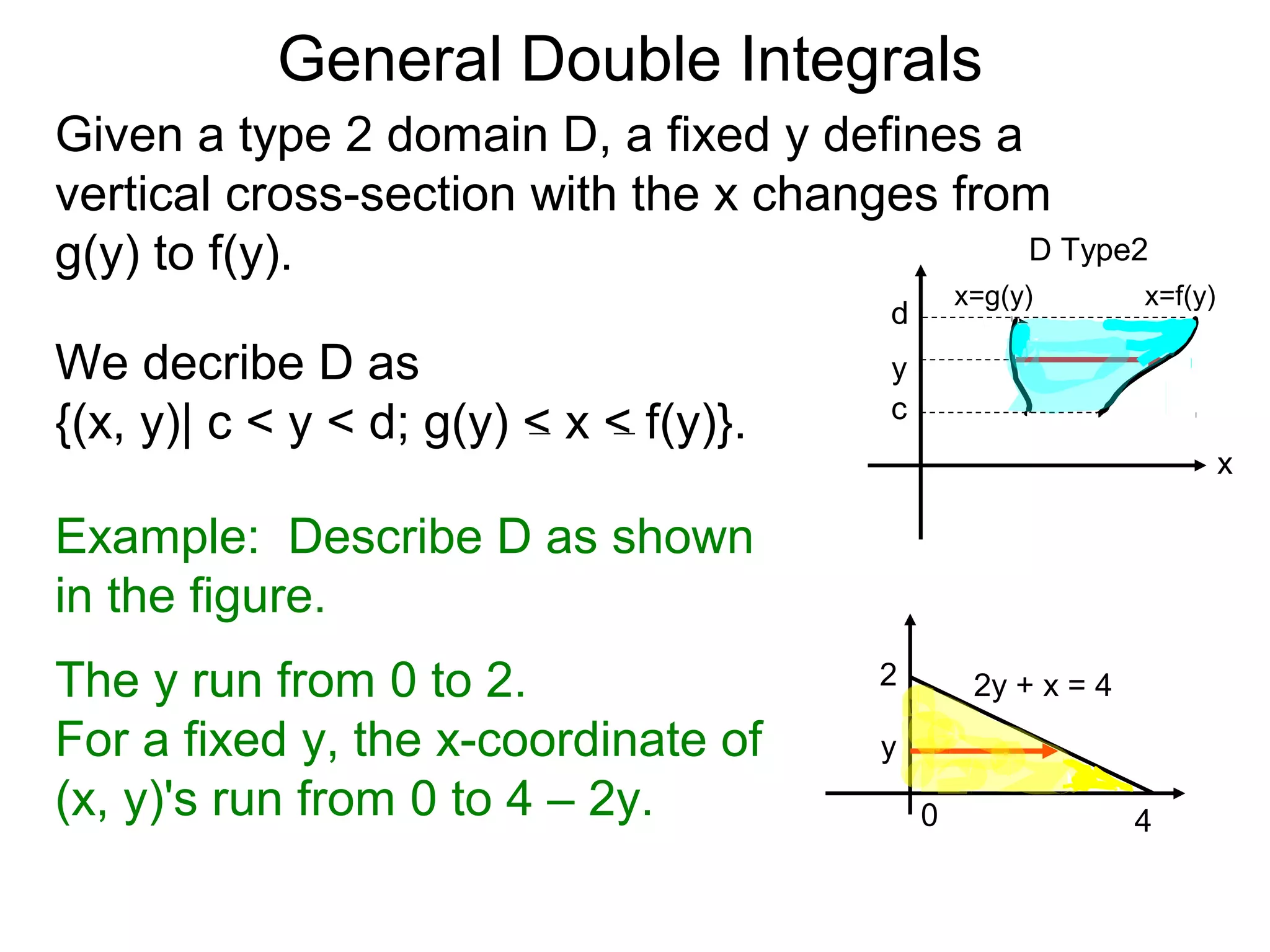
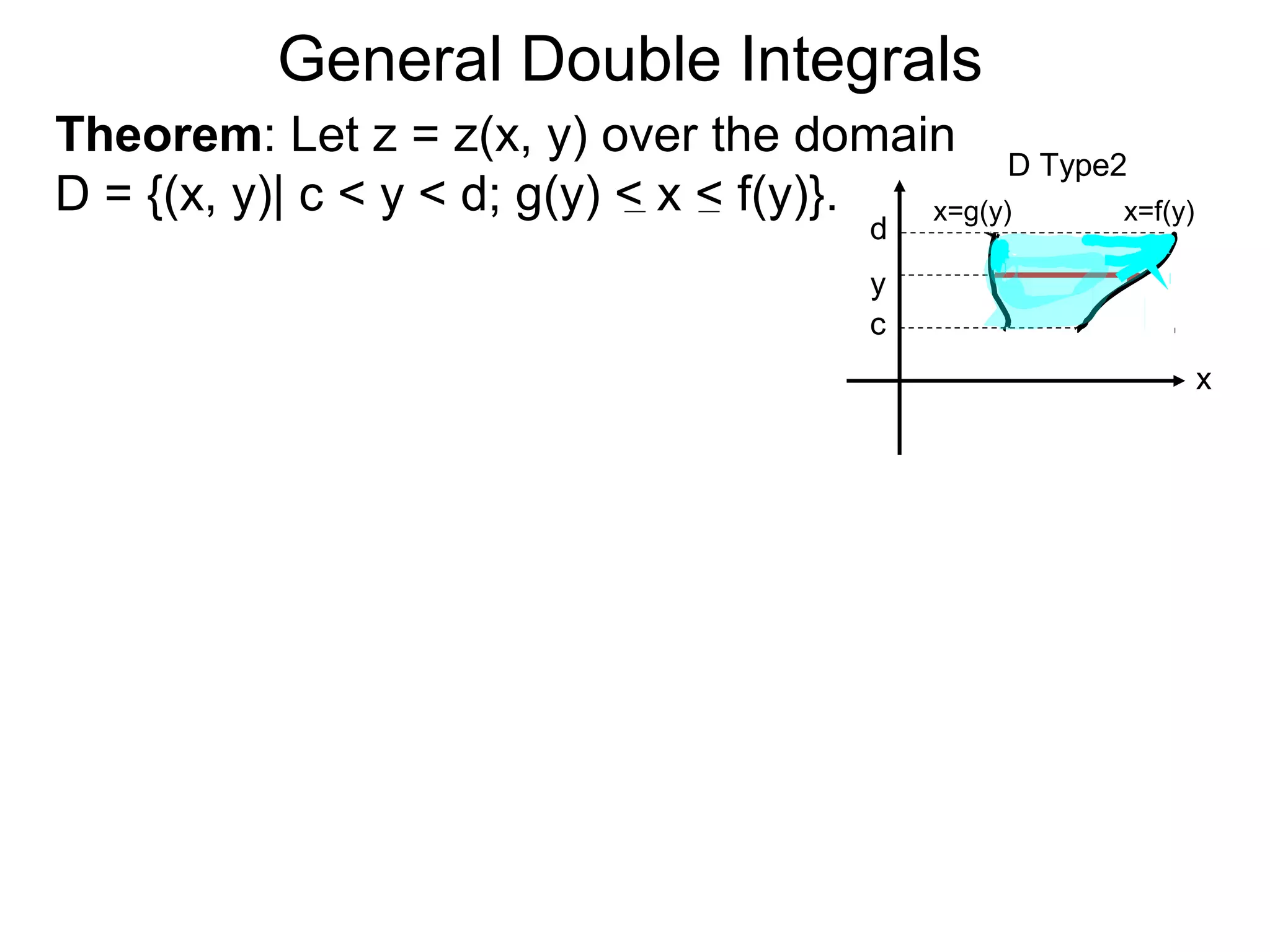
42. General Double Integrals
Theorem: Let z = z(x, y) over the domain
D = {(x, y)| c < y < d; g(y) < x < f(y)}.
Then
∫ f(x, y)dA =∫ ∫ z(x, y)dx ]dy.
y=c
d
∫x=g(y)
f(y)
[
D
x=f(y)x=g(y)
d
c
D Type2
x
y

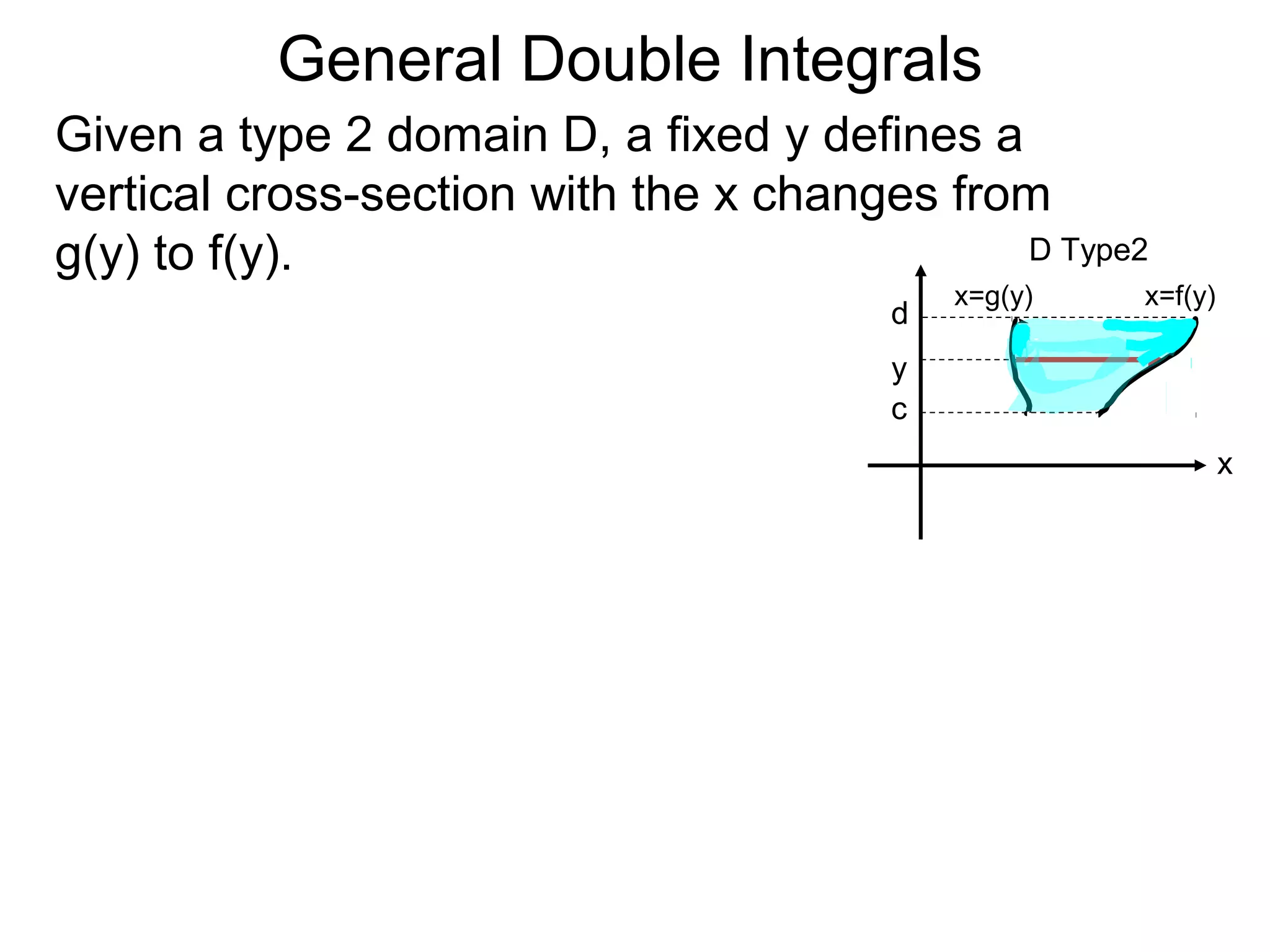
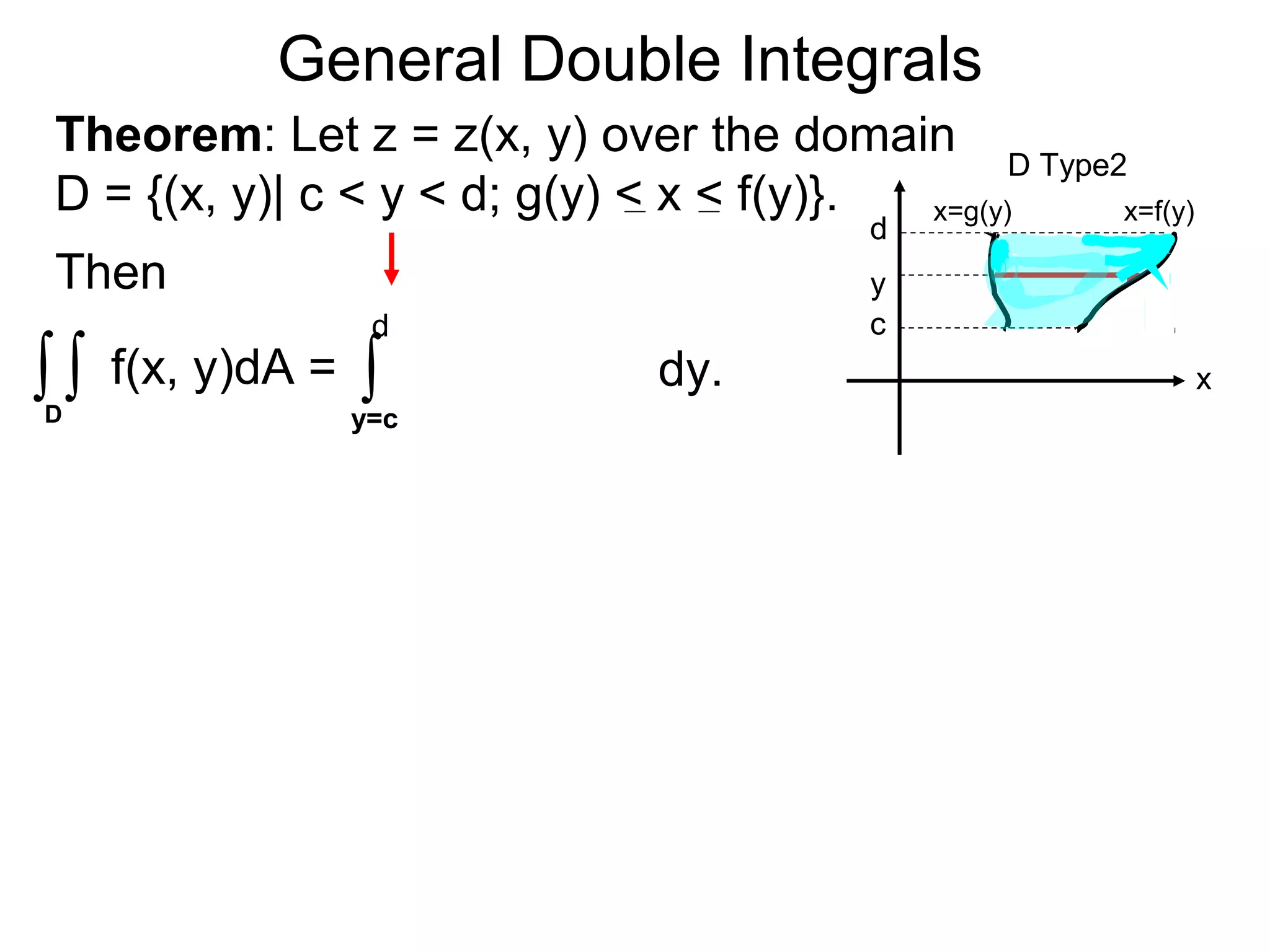
43. General Double Integrals
Theorem: Let z = z(x, y) over the domain
D = {(x, y)| c < y < d; g(y) < x < f(y)}.
Then
∫ f(x, y)dA =∫ ∫ z(x, y)dx ]dy.
y=c
d
∫x=g(y)
f(y)
[
The order of the integration is set according to the the
description of the domain D with ∫ dy outside and ∫ dx
inside to be calculated first.
D
x=f(y)x=g(y)
d
c
D Type2
x
y

44. General Double Integrals
Theorem: Let z = z(x, y) over the domain
D = {(x, y)| c < y < d; g(y) < x < f(y)}.
Then
∫ f(x, y)dA =∫ ∫ z(x, y)dx ]dy.
y=c
d
∫x=g(y)
f(y)
[
The order of the integration is set according to the the
description of the domain D with ∫ dy outside and ∫ dx
inside to be calculated first.
Again, if D is the rectangle [a, b] x [c, d], then
D = {c < y < d; a < x < b } and the double integral is
∫ f(x, y)dA =∫ ∫ z(x, y)dx ]dy.
y=c
d
∫x=a
b
[
D
D
x=f(y)x=g(y)
d
c
D Type2
x
y

45. General Double Integrals
Example: D is bounded by x = 2y, and x = y2
+ 1 from y = 0
to y = 1. Draw D. Find the volume of z = 2x + y over D.

46. General Double Integrals
Example: D is bounded by x = 2y, and x = y2
+ 1 from y = 0
to y = 1. Draw D. Find the volume of z = 2x + y over D.
To solve for intersection, set 2y = y2
+ 1
and get y =1.

47. General Double Integrals
Example: D is bounded by x = 2y, and x = y2
+ 1 from y = 0
to y = 1. Draw D. Find the volume of z = 2x + y over D.
To solve for intersection, set 2y = y2
+ 1
and get y =1.
1 x = y2
+ 1
x = 2y

48. General Double Integrals
Example: D is bounded by x = 2y, and x = y2
+ 1 from y = 0
to y = 1. Draw D. Find the volume of z = 2x + y over D.
So D is bounded to the right by y2
+ 1,
to the left 2y, from y = 0 to y = 1.
To solve for intersection, set 2y = y2
+ 1
and get y =1.
1 x = y2
+ 1
x = 2y

49. General Double Integrals
Example: D is bounded by x = 2y, and x = y2
+ 1 from y = 0
to y = 1. Draw D. Find the volume of z = 2x + y over D.
So D is bounded to the right by y2
+ 1,
to the left 2y, from y = 0 to y = 1.
To solve for intersection, set 2y = y2
+ 1
and get y =1.
To set the iterated integral, write D in
correct order as
{(x, y)| 0 < y < 1;
1 x = y2
+ 1
x = 2y

50. General Double Integrals
Example: D is bounded by x = 2y, and x = y2
+ 1 from y = 0
to y = 1. Draw D. Find the volume of z = 2x + y over D.
So D is bounded to the right by y2
+ 1,
to the left 2y, from y = 0 to y = 1.
To solve for intersection, set 2y = y2
+ 1
and get y =1.
To set the iterated integral, write D in
correct order as
{(x, y)| 0 < y < 1; 2y < x < y2
+1 }
1 x = y2
+ 1
x = 2y

51. General Double Integrals
Example: D is bounded by x = 2y, and x = y2
+ 1 from y = 0
to y = 1. Draw D. Find the volume of z = 2x + y over D.
So D is bounded to the right by y2
+ 1,
to the left 2y, from y = 0 to y = 1.
To solve for intersection, set 2y = y2
+ 1
and get y =1.
To set the iterated integral, write D in
correct order as
{(x, y)| 0 < y < 1; 2y < x < y2
+1 }
then set the integral in this order:
dy∫y=0
1
1 x = y2
+ 1
x = 2y
2x + y dx
x=y2
+1
∫x=2y

52. General Double Integrals
dy∫y=0
1
2x + y dx
x=y2
+1
∫x=2y
1 x = y2
+ 1
x = 2y

53. General Double Integrals
=∫y=0
1
dy∫y=0
1
2x + y dx
x=y2
+1
∫x=2y
x2
+ yx| dy
x=2y
x=y2
+1
1 x = y2
+ 1
x = 2y

54. General Double Integrals
=∫y=0
1
= (y2
+ 1)2
+ y(y2
+1) – (2y)2
– y(2y)dy∫y=0
1
dy∫y=0
1
2x + y dx
x=y2
+1
∫x=2y
x2
+ yx| dy
x=2y
x=y2
+1
1 x = y2
+ 1
x = 2y

55. General Double Integrals
=∫y=0
1
= (y2
+ 1)2
+ y(y2
+1) – (2y)2
– y(2y)dy∫y=0
1
=∫y=0
1
dy∫y=0
1
2x + y dx
x=y2
+1
∫x=2y
x2
+ yx| dy
x=2y
x=y2
+1
1 x = y2
+ 1
x = 2y
y4
+ y3
– 4y2
+ y + 1 dy

56. General Double Integrals
=∫y=0
1
= (y2
+ 1)2
+ y(y2
+1) – (2y)2
– y(2y)dy∫y=0
1
=∫y=0
1
dy∫y=0
1
2x + y dx
x=y2
+1
∫x=2y
x2
+ yx| dy
x=2y
x=y2
+1
1 x = y2
+ 1
x = 2y
y4
+ y3
– 4y2
+ y + 1 dy
=
37
60

57. General Double Integrals
Its possible that a
domain is both type 1
and type 2:

58. General Double Integrals
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
2
D

59. General Double Integrals
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
Let f(x, y) = e .
2
D
x2

60. General Double Integrals
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
Let f(x, y) = e . The double integral may be set in
two ways over D.
2
D
x2

61. General Double Integrals
= dy∫y=0
2
dx
x=1
∫x=y/2
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
Let f(x, y) = e . The double integral may be set in
two ways over D. If we set the iterated integral as
∫ D
dA∫
2
D
x2
x2
e
x2
e

62. General Double Integrals
= dy∫y=0
2
dx
x=1
∫x=y/2
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
Let f(x, y) = e . The double integral may be set in
two ways over D. If we set the iterated integral as
∫D
dA∫
2
D
it won't be not computable.
x2
x2
e
x2
e

63. General Double Integrals
= dy∫y=0
2
dx
x=1
∫x=y/2
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
Let f(x, y) = e . The double integral may be set in
two ways over D. If we set the iterated integral as
∫D
dA∫
2
D
it won't be not computable. But if we switch the order:
x2
x2
e
x2
e
=∫D
dA∫
x2
e

64. General Double Integrals
= dy∫y=0
2
dx
x=1
∫x=y/2
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
Let f(x, y) = e . The double integral may be set in
two ways over D. If we set the iterated integral as
∫D
dA∫
2
D
it won't be not computable. But if we switch the order:
x2
x2
e
x2
e
= dx∫x=0
1
dy
y=2x
∫y=0
∫D
dA∫
x2
e
x2
e

65. General Double Integrals
= dy∫y=0
2
dx
x=1
∫x=y/2
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
Let f(x, y) = e . The double integral may be set in
two ways over D. If we set the iterated integral as
∫D
dA∫
2
D
it won't be not computable. But if we switch the order:
x2
x2
e
x2
e
= dx∫x=0
1
dy
y=2x
∫y=0
∫D
dA∫
x2
e
x2
e = dx∫x=0
1 y=2x
y=0
x2
e y|

66. General Double Integrals
= dy∫y=0
2
dx
x=1
∫x=y/2
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
Let f(x, y) = e . The double integral may be set in
two ways over D. If we set the iterated integral as
∫D
dA∫
2
D
it won't be not computable. But if we switch the order:
x2
x2
e
x2
e
= dx∫x=0
1
dy
y=2x
∫y=0
∫D
dA∫
x2
e
x2
e = dx∫x=0
1 y=2x
y=0
x2
e y| = dx∫x=0
1
x2
2xe

67. General Double Integrals
= dy∫y=0
2
dx
x=1
∫x=y/2
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
Let f(x, y) = e . The double integral may be set in
two ways over D. If we set the iterated integral as
∫D
dA∫
2
D
it won't be not computable. But if we switch the order:
x2
x2
e
x2
e
= dx∫x=0
1
dy
y=2x
∫y=0
∫D
dA∫
x2
e
x2
e = dx∫x=0
1 y=2x
y=0
x2
e y| = dx∫x=0
1
2xe
x=0
1
x2
e |= = e – 1
x2

68. General Double Integrals
= dy∫y=0
2
dx
x=1
∫x=y/2
Its possible that a
domain is both type 1
and type 2:
y=2x or x=y/2
1
Let f(x, y) = e . The double integral may be set in
two ways over D. If we set the iterated integral as
∫D
dA∫
2
D
it won't be not computable. But if we switch the order:
x2
x2
e
x2
e
= dx∫x=0
1
dy
y=2x
∫y=0
∫D
dA∫
x2
e
x2
e = dx∫x=0
1 y=2x
y=0
x2
e y| = dx∫x=0
1
2xe
x=0
1
x2
e |= = e – 1
We say we reverse the order of integration in this case
x2

69. General Double Integrals
The area of a 2D shape D is the same numerically
as the volume of the cylinder with height 1 over D.

70. General Double Integrals
The area of a 2D shape D is the same numerically
as the volume of the cylinder with height 1 over D.
=Area Volume
1
(numerically)

71. General Double Integrals
The area of a 2D shape D is the same numerically
as the volume of the cylinder with height 1 over D.
Therefore we may compute area of D by computing
the volume of the cylinder with ht=1 over D.
=Area Volume
1
(numerically)

72. General Double Integrals
The area of a 2D shape D is the same numerically
as the volume of the cylinder with height 1 over D.
Therefore we may compute area of D by computing
the volume of the cylinder with ht=1 over D.
Example:
Find the area
enclosed by y = x2
and y = 2x + 3.
=Area Volume
1
(numerically)

73. General Double Integrals
The area of a 2D shape D is the same numerically
as the volume of the cylinder with height 1 over D.
Therefore we may compute area of D by computing
the volume of the cylinder with ht=1 over D.
Example:
Find the area
enclosed by y = x2
and y = 2x + 3.
=Area Volume
1
(numerically)
-1 3
1

74. General Double Integrals
The area of a 2D shape D is the same numerically
as the volume of the cylinder with height 1 over D.
Therefore we may compute area of D by computing
the volume of the cylinder with ht=1 over D.
Example:
Find the area
enclosed by y = x2
and y = 2x + 3.
=Area Volume
1
(numerically)
Set x2
= 2x + 3, we get x = -1, and 3. Set the integral
-1 3
1

75. General Double Integrals
Let z = f(x, y) = 1.
x=-1
-1 3
1

76. General Double Integrals
Let z = f(x, y) = 1. It defines the cylinder whose
volume is the integral:
dx∫x=-1
3
dy
y=2x+3
∫y=x2
1
x=-1
-1 3
1

77. General Double Integrals
Let z = f(x, y) = 1. It defines the cylinder whose
volume is the integral:
dx∫x=-1
3
dy
y=2x+3
∫y=x2
1 = dx∫x=-1
3
y |
y=2x+3
y=x2
=
x=-1
-1 3
1

78. General Double Integrals
Let z = f(x, y) = 1. It defines the cylinder whose
volume is the integral:
dx∫x=-1
3
dy
y=2x+3
∫y=x2
1 = dx∫x=-1
3
y |
y=2x+3
y=x2
= dx∫x=-1
3
2x + 3 – x2
x=-1
-1 3
1

79. General Double Integrals
Let z = f(x, y) = 1. It defines the cylinder whose
volume is the integral:
dx∫x=-1
3
dy
y=2x+3
∫y=x2
1 = dx∫x=-1
3
y |
y=2x+3
y=x2
= dx∫x=-1
3
2x + 3 – x2
= x2
+ 3x – x3
/3 |
x=-1
3
=
-1 3
1
x=-1

80. General Double Integrals
Let z = f(x, y) = 1. It defines the cylinder whose
volume is the integral:
dx∫x=-1
3
dy
y=2x+3
∫y=x2
1 = dx∫x=-1
3
y |
y=2x+3
y=x2
= dx∫x=-1
3
2x + 3 – x2
= x2
+ 3x – x3
/3 |
x=-1
3
=
28
3
-1 3
1
x=-1
which is the measurement of the area.

81. General Double Integrals
Let z = f(x, y) = 1. It defines the cylinder whose
volume is the integral:
dx∫x=-1
3
dy
y=2x+3
∫y=x2
1 = dx∫x=-1
3
y |
y=2x+3
y=x2
= dx∫x=-1
3
2x + 3 – x2
= x2
+ 3x – x3
/3 |
x=-1
3
=
28
3
-1 3
1
x=-1
which is the measurement of the area.
To summarize: ∫ dA = area of D.∫ 1
D