CR
Uploaded bychitra raju
PPTX, PDF4,552 views

Overlap save method and overlap add method in dsp

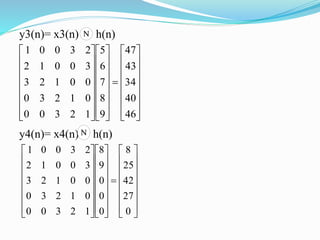
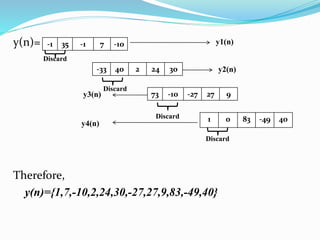
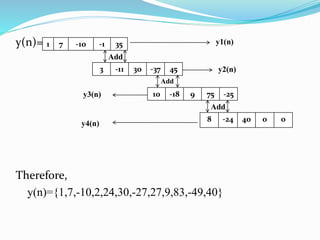
The document is a lecture note on digital signal processing, specifically focusing on the overlap save and overlap add methods used for linear convolution with finite impulse response (FIR) filters. It explains how to evaluate the discrete convolution of long signals with FIR filters by dividing the input signal into blocks and provides examples for each method. The content includes detailed examples demonstrating the calculations necessary for applying both the overlap save and overlap add techniques.

Embed presentation

Downloaded 20 times
DIGITAL SIGNAL PROCESSING By Mrs.R.Chitra, Assistant Professor(SS), Department of ECE, School of Engineering, Avinashilingam Institute for Home Science and Higher Education for Women, Coimbatore
Topics to be Covered: 1. OVERLAP SAVE METHOD 2. OVERLAP ADD METHOD 3. LINEAR CONVOLUTION
OVERLAP SAVE METHOD:  Overlap–save is the traditional name for an efficient way to evaluate the discrete convolution between a very long signal x(n) and a finite impulse response FIR filter h(n)  In this method the input sequence is divided into blocks of data of size N=L+M-1.where L= length of an input sequence and M=the length of an impulse response  Each block consist of last (M-1) data points of previous block followed by L new data points to form a data sequence of length N=L+M-1.  For first block, M-1 points are set to zero. The input sequence can be divided into blocks as X1(n) = {0,0,x(0),x(1),x(2)} M-1=2zeros
X2(n) = {x(1),x(2),x(3),x(4),x(5)} Last two data points from previous block X3(n) = {x(4),x(5),x(6),x(7),x(8)} X4(n) = {x(7),x(8),x(9),x(10),x(11)} X5(n) = {x(10),x(11),x(12),x(13),x(14)} X6(n) = {x(13),x(14),0,0,0} Thus, Y1(n)=x1(n) h(n)={y1(0),y1(1),y1(2),y1(3),y1(4)} Y2(n)=x2(n) h(n)={y2(0),y2(1),y2(2),y2(3),y2(4)}N N
Y3(n)=x3(n) h(n)={y3(0),y3(1),y3(2),y3(3),y3(4)} Y4(n)=x4(n) h(n)={y4(0),y4(1),y4(2),y4(3),y4(4)} Y5(n)=x5(n) h(n)={y5(0),y5(1),y5(2),y5(3),y5(4)} Y6(n)=x6(n) h(n)={y6(0),y6(1),y6(2),y6(3),y6(4)} Therefore, the output blocks are abutted together to get Y(n)={y1(2),y1(3),y1(4),y2(2),y2(3),y2(4),y3(2),y3(3), y3(4),y4(4),y5(2),y5(3),y5(4),y6(2),y6(3)} N N N N
EXAMPLE 1: Determine the output of linear FIR filter whose impulse response is h(n)={1,2,3} and the input signal is x(n)= {1,2,3,4,5,6,7,8,9} using over lap save method. SOLUTION: Given, x(n)= {1,2,3,4,5,6,7,8,9} & h(n)={1,2,3} Therefore, L=9;M=3; Adding M-1 zeros in x1(n),we get x1(n)={0,0,1,2,3} x2(n)={2,3,4,5,6} x3(n)={5,6,7,8,9} x4(n)={8,9,0,0,0} h(n)={1,2,3,0,0}
By circular convolution, y1(n)= x1(n) h(n) y2(n)= x2(n) h(n) N N                                                  10 4 1 9 12 3 2 1 0 0 13300 01230 00123 30012 23001                                                  28 22 16 25 29 6 5 4 3 2 13300 01230 00123 30012 23001
y3(n)= x3(n) h(n) y4(n)= x4(n) h(n) N N                                                  46 40 34 43 47 9 8 7 6 5 12300 01230 00123 30012 23001                                                  0 27 42 25 8 0 0 0 9 8 12300 01230 00123 30012 23001
y(n)= Therefore, y(n)={1,4,10,16,22,28,34,40,46,42,27} 12 9 1 4 10 29 25 16 22 28 8 25 42 27 0 Add y3(n) y2(n) y1(n) 47 43 34 40 46 y4(n) Discard Discard Discard Discard
EXAMPLE 2: Determine the output of linear FIR filter whose impulse response is h(n)={1,-3,5} and the input signal is x(n)= {-1,4,7,3,-2,9,10,12,-5,8} using over lap save method. SOLUTION: Given, x(n)= {-1,4,7,3,-2,9,10,12,-5,8} & h(n)={1,-3,5} Therefore, L=9;M=3; Adding M-1 zeros in x1(n),we get x1(n)={0,0,-1,4,7} x2(n)={4,7,3,-2,9} x3(n)={-2,9,10,12,-5} x4(n)={12,-5,8,0,0} h(n)={1,-3,5,0,0}
By circular convolution, y1(n)= x1(n) h(n) y2(n)= x2(n) h(n) N N                                                           10 7 1 35 1 7 4 1 0 0 13500 01350 00135 50013 35001                                                        30 24 2 40 33 9 2 3 7 4 13500 01350 00135 50013 35001
y3(n)= x3(n) h(n) y4(n)= x4(n) h(n) N N                                                           9 27 27 10 73 5 12 10 9 2 13500 01350 00135 50013 35001                                                         40 49 83 0 1 0 0 8 5 12 13500 01350 00135 50013 35001
y(n)= Therefore, y(n)={1,7,-10,2,24,30,-27,27,9,83,-49,40} -1 35 -1 7 -10 -33 40 2 24 30 1 0 83 -49 40 Add y3(n) y2(n) y1(n) 73 -10 -27 27 9 y4(n) Discard Discard Discard Discard
OVERLAP ADD METHOD:  The length of the sequence is be Ls and the length of the impulse response is M.  The sequence is divided into blocks of data size having length L and M-1.  Zeros are appended to it make the data size of L+M-1. Let the output blocks are of the form, y1(n)={y1(0),y1(1),…….,y1(L-1),y1(L),….,y1(N-1)} y2(n)={y2(0),y2(1),……,y2(L-1),y2(L),….,y2(N-1)} y3(n)={y3(0),y3(1),…….,y3(L-1),y3(L),……,y3(N-1)} the output sequence is Y(n)={y1(0),y1(1),….,y1(L-1),y1(L)+y2(0),….,y1(N-1)+ y2(M-2),y2(M),……,y2(L)+y3(0),y2(L+1)+y3(1),….,y3(N-1)}
EXAMPLE 1: Determine the output of linear FIR filter whose impulse response is h(n)={1,2,3} and the input signal is x(n)= {1,2,3,4,5,6,7,8,9} using over lap add method. SOLUTION: Given, x(n)= {1,2,3,4,5,6,7,8,9} & h(n)={1,2,3} Therefore, L=9;M=3; Adding M-1 zero,we get x1(n)={1,2,3,0,0} x2(n)={4,5,6,0,0} x3(n)={7,8,9,0,0} h(n)={1,2,3,0,0}
By circular convolution, y1(n)= x1(n) h(n) y2(n)= x2(n) h(n) N N                                                  18 27 28 13 4 0 0 6 5 4 13300 01230 00123 30012 23001                                                  9 12 10 4 1 0 0 3 2 1 13300 01230 00123 30012 23001
y3(n)= x3(n) h(n) y(n)= Therefore, y(n)={1,4,10,16,22,28,34,40,46,42,27} N                                                  27 42 46 22 7 0 0 9 8 7 13300 01230 00123 30012 23001 1 4 10 12 9 4 13 28 27 18 7 22 46 42 27 Add Add y3(n) y2(n) y1(n)
EXAMPLE 2: Determine the output of linear FIR filter whose impulse response is h(n)={1,-3,5} and the input signal is x(n)= {-1,4,7,3,-2,9,10,12,-5,8} using over lap add method. SOLUTION: Given, x(n)= {-1,4,7,3,-2,9,10,12,-5,8} & h(n)={1,-3,5} Therefore, L=9;M=3; Adding M-1 zeros, we get x1(n)={-1,4,7,0,0} x2(n)={3,-2,9,0,0} x3(n)={10,12,-5,0,0} x4(n)={8,0,0,0,0} h(n)={1,-3,5,0,0}
By circular convolution, y1(n)= x1(n) h(n) y2(n)= x2(n) h(n) N N                                                          45 37 30 11 3 0 0 9 2 3 13500 01350 00135 50013 35001                                                        35 1 10 7 1 0 0 7 4 1 13500 01350 00135 50013 35001
y3(n)= x3(n) h(n) y4(n)= x4(n) h(n) N N                                                          25 75 9 18 10 0 0 5 12 10 13500 01350 00135 50013 35001                                                        0 0 40 24 8 0 0 0 0 8 13500 01350 00135 50013 35001
y(n)= Therefore, y(n)={1,7,-10,2,24,30,-27,27,9,83,-49,40} 1 7 -10 -1 35 3 -11 30 -37 45 8 -24 40 0 0 Add Add y3(n) y2(n) y1(n) 10 -18 9 75 -25 Add Add y4(n)
LINEAR CONVOLUTION FROM CIRCULAR CONVOLUTION: • Let us consider two finite duration sequences x(n) and h(n). The duration of x(n) is L and y(n) is M samples. The linear convolution of x(n) and h(n) is given by the formula where y(n) is a finite duration of sequence of L+M-1 samples. The circular convolution of x(n) and h(n) give N samples where N=Max(L,M). Consider two sequences x(n) and h(n) having sequence length L=5 and M=3 respectively as shown in the figure. x(n) L=5 0 1 2 3 4     k knhkxny )()()(
h(n) M=3 0 1 2 The linear convolution of x(n) and h(n) consist of 5+3-1=7 points. 3 3 3 y(n)=x(n)*h(n) 2 2 1 1 0 1 2 3 4 5 6 The circular convolution of x(n) and h(n) consist of 5 points short of M-1=2 points. Therefore the circular convolution will contain corrupted points due to time domain aliasing. These points are first (M-1) points as shown in the figure. Aliasing y(0)&y(5) y(1)&y(6) 0 1 2 3 4
EXAMPLE:
Thus, linear convolution is done.
THANK YOU!!!

More Related Content

PPTX
Overlap Add, Overlap Save(digital signal processing)
byGourab Ghosh
 
PDF
Design of IIR filters
byop205
 
PDF
Dsp U Lec10 DFT And FFT
bytaha25
 
PDF
Circular Convolution
bySarang Joshi
 
PPTX
Multirate DSP
by@zenafaris91
 
PPT
Dif fft
bySaleem Almaqashi
 
PDF
DSP_FOEHU - Lec 07 - Digital Filters
byAmr E. Mohamed
 
PDF
Decimation and Interpolation
byFernando Ojeda
 
Overlap Add, Overlap Save(digital signal processing)
byGourab Ghosh
 
Design of IIR filters
byop205
 
Dsp U Lec10 DFT And FFT
bytaha25
 
Circular Convolution
bySarang Joshi
 
Multirate DSP
by@zenafaris91
 
Dif fft
bySaleem Almaqashi
 
DSP_FOEHU - Lec 07 - Digital Filters
byAmr E. Mohamed
 
Decimation and Interpolation
byFernando Ojeda
 

What's hot

PPTX
Discrete Fourier Transform
byAbhishek Choksi
 
PPTX
Radix-2 DIT FFT
bySarang Joshi
 
PPT
Decimation in time and frequency
bySARITHA REDDY
 
PDF
EC8562 DSP Viva Questions
byssuser2797e4
 
PPTX
Overview of sampling
bySagar Kumar
 
PPTX
Fir filter design using windows
bySarang Joshi
 
PDF
Question paper with solution the 8051 microcontroller based embedded systems...
bymanishpatel_79
 
PPTX
DPCM
bysuryateja swamy
 
PPTX
Design of Filters PPT
byImtiyaz Rashed
 
PPTX
Convolutional codes
byAbdullaziz Tagawy
 
PPTX
Periodic vs. aperiodic signal
byTahsin Abrar
 
PPTX
convolution
byAbhishekLalkiya
 
PPTX
discrete time signals and systems
byZlatan Ahmadovic
 
PPTX
Microwave oscillator design
byImane Haf
 
PDF
Sun transit outage
byRCC Institute of Information Technology
 
PPT
Antenna PARAMETERS
byAJAL A J
 
PDF
DSP_2018_FOEHU - Lec 06 - FIR Filter Design
byAmr E. Mohamed
 
PPTX
IS-95 Cdma
byyogesh singh
 
PPTX
Comparsion of M-Ary psk,fsk,qapsk.pptx
bykeshav11845
 
PPTX
FILTER DESIGN
bynaimish12
 
Discrete Fourier Transform
byAbhishek Choksi
 
Radix-2 DIT FFT
bySarang Joshi
 
Decimation in time and frequency
bySARITHA REDDY
 
EC8562 DSP Viva Questions
byssuser2797e4
 
Overview of sampling
bySagar Kumar
 
Fir filter design using windows
bySarang Joshi
 
Question paper with solution the 8051 microcontroller based embedded systems...
bymanishpatel_79
 
DPCM
bysuryateja swamy
 
Design of Filters PPT
byImtiyaz Rashed
 
Convolutional codes
byAbdullaziz Tagawy
 
Periodic vs. aperiodic signal
byTahsin Abrar
 
convolution
byAbhishekLalkiya
 
discrete time signals and systems
byZlatan Ahmadovic
 
Microwave oscillator design
byImane Haf
 
Sun transit outage
byRCC Institute of Information Technology
 
Antenna PARAMETERS
byAJAL A J
 
DSP_2018_FOEHU - Lec 06 - FIR Filter Design
byAmr E. Mohamed
 
IS-95 Cdma
byyogesh singh
 
Comparsion of M-Ary psk,fsk,qapsk.pptx
bykeshav11845
 
FILTER DESIGN
bynaimish12
 

Similar to Overlap save method and overlap add method in dsp

PPTX
Digital signal processing
byReachLocal Services India
 
PPTX
Overlapadd using convolution
byMeghaThakur26
 
PPT
Ecte401 notes week3
bysubhasree konar
 
PDF
A Novel Methodology for Designing Linear Phase IIR Filters
byIDES Editor
 
PDF
A novel approach for high speed convolution of finite
byeSAT Publishing House
 
PDF
Mlab i
byHarsh Kumar
 
PDF
A novel approach for high speed convolution of finite and infinite length seq...
byeSAT Journals
 
PPTX
Dsp GA (1).pptx
bybhavanags5
 
PDF
Multirate sim
byAlim Sheikh
 
PDF
DSP Lab Manual (10ECL57) - VTU Syllabus (KSSEM)
byRavikiran A
 
PDF
Presentation Sampling adn Reconstruction.pdf
bywerom2
 
PDF
DSP lecture notes on for akuru which will
byAkhilesh Mishra
 
PDF
Dt convolution
byReggie Powe
 
PPTX
Time domain representation of signals and systems
bynatureshorts193
 
PDF
DSP - Realization of Finite Impulse Response Filter
byShiny Christobel
 
PPTX
Time domain representation or analysis of DSP
bynatureshorts193
 
PDF
Matlab programs
byPrakash Rout
 
PDF
omp-and-k-svd - Gdc2013
byManchor Ko
 
PDF
Lt2419681970
byIJERA Editor
 
PDF
EC8553 Discrete time signal processing
byssuser2797e4
 
Digital signal processing
byReachLocal Services India
 
Overlapadd using convolution
byMeghaThakur26
 
Ecte401 notes week3
bysubhasree konar
 
A Novel Methodology for Designing Linear Phase IIR Filters
byIDES Editor
 
A novel approach for high speed convolution of finite
byeSAT Publishing House
 
Mlab i
byHarsh Kumar
 
A novel approach for high speed convolution of finite and infinite length seq...
byeSAT Journals
 
Dsp GA (1).pptx
bybhavanags5
 
Multirate sim
byAlim Sheikh
 
DSP Lab Manual (10ECL57) - VTU Syllabus (KSSEM)
byRavikiran A
 
Presentation Sampling adn Reconstruction.pdf
bywerom2
 
DSP lecture notes on for akuru which will
byAkhilesh Mishra
 
Dt convolution
byReggie Powe
 
Time domain representation of signals and systems
bynatureshorts193
 
DSP - Realization of Finite Impulse Response Filter
byShiny Christobel
 
Time domain representation or analysis of DSP
bynatureshorts193
 
Matlab programs
byPrakash Rout
 
omp-and-k-svd - Gdc2013
byManchor Ko
 
Lt2419681970
byIJERA Editor
 
EC8553 Discrete time signal processing
byssuser2797e4
 

More from chitra raju

PPTX
What is Dishwasher and its Classifications.pptx
bychitra raju
 
PPTX
Sensor tasking and control
bychitra raju
 
PPTX
Fast fourier transform
bychitra raju
 
PPTX
Molecular electronic devices
bychitra raju
 
PPTX
Micro Electro Mechanical Systems
bychitra raju
 
PPTX
Nano Robots
bychitra raju
 
PPTX
Digital signal processing
bychitra raju
 
PPTX
Classification of signals
bychitra raju
 
What is Dishwasher and its Classifications.pptx
bychitra raju
 
Sensor tasking and control
bychitra raju
 
Fast fourier transform
bychitra raju
 
Molecular electronic devices
bychitra raju
 
Micro Electro Mechanical Systems
bychitra raju
 
Nano Robots
bychitra raju
 
Digital signal processing
bychitra raju
 
Classification of signals
bychitra raju
 

Recently uploaded

PDF
Module 4 python programming-1BPLCK105B-2025 by Dr.SV.pdf
bySURESHA V
 
PDF
Decision-Support-Systems-and-Decision-Making-Processes.pdf
byPatankarNikhil
 
PPTX
Theory to Practice of Unsaturated Soil Mechanics-1.pptx
byMahmoodKhalid11
 
PDF
WTE Infra Projects Pvt. Ltd. Company Profile 2026 – Water & Wastewater Treatm...
byWTE Infra Projects Pvt. Ltd
 
PPTX
Integrating Azure Event Services_ Event Grid, Event Hubs, and Service Bus.pptx
byADITYASHARMA423788
 
PPTX
Energy_Conservation_in_Cement_Factories.pptx
bysibirajmurugan8
 
PDF
Chad Ayach - An Accomplished Mechanical Engineer
byChad Ayach
 
PPTX
This Bearing Didn’t Fail Suddenly — How Vibration Data Predicts Failure Month...
byMaintWiz Technologies Private Limited
 
PDF
Model QP 2025 scheme Q &A- Module 1 and 2.pdf
bySURESHA V
 
PPTX
How Does LNG Regasification Work | INOXCVA
byINOXCVA
 
PDF
Manual de instalacion de notifire NFS320
byMarcoPolitoPerez
 
PDF
engineering management chapter 5 ppt presentation
byericaangelatoledo06
 
PPTX
Distresses in Road Flexible pavement.pptx
byMahmoodKhalid11
 
PDF
Ericsson 6230 Training Module Document.pdf
byMd Bellal Hossain
 
PDF
Lifting Operations Safety and Risk Control
bymanju774
 
PPTX
Optimized access control techniques in Cloud Computing with Security and Scal...
bymareswariesteru
 
PPTX
Basic Volume Mass Relationship and unit weight as function of volumetric wate...
byMahmoodKhalid11
 
PDF
NS unit wise unit wise 1 -5 so prepare,.
bykumaransudhan1512
 
PPTX
ISO 13485.2016 Awareness's Training material
byPrakashSivan
 
PPTX
Lubrication Neglect Causes More Downtime Than AI Ever Will Why Maintenance Fu...
byMaintWiz Technologies Private Limited
 
Module 4 python programming-1BPLCK105B-2025 by Dr.SV.pdf
bySURESHA V
 
Decision-Support-Systems-and-Decision-Making-Processes.pdf
byPatankarNikhil
 
Theory to Practice of Unsaturated Soil Mechanics-1.pptx
byMahmoodKhalid11
 
WTE Infra Projects Pvt. Ltd. Company Profile 2026 – Water & Wastewater Treatm...
byWTE Infra Projects Pvt. Ltd
 
Integrating Azure Event Services_ Event Grid, Event Hubs, and Service Bus.pptx
byADITYASHARMA423788
 
Energy_Conservation_in_Cement_Factories.pptx
bysibirajmurugan8
 
Chad Ayach - An Accomplished Mechanical Engineer
byChad Ayach
 
This Bearing Didn’t Fail Suddenly — How Vibration Data Predicts Failure Month...
byMaintWiz Technologies Private Limited
 
Model QP 2025 scheme Q &A- Module 1 and 2.pdf
bySURESHA V
 
How Does LNG Regasification Work | INOXCVA
byINOXCVA
 
Manual de instalacion de notifire NFS320
byMarcoPolitoPerez
 
engineering management chapter 5 ppt presentation
byericaangelatoledo06
 
Distresses in Road Flexible pavement.pptx
byMahmoodKhalid11
 
Ericsson 6230 Training Module Document.pdf
byMd Bellal Hossain
 
Lifting Operations Safety and Risk Control
bymanju774
 
Optimized access control techniques in Cloud Computing with Security and Scal...
bymareswariesteru
 
Basic Volume Mass Relationship and unit weight as function of volumetric wate...
byMahmoodKhalid11
 
NS unit wise unit wise 1 -5 so prepare,.
bykumaransudhan1512
 
ISO 13485.2016 Awareness's Training material
byPrakashSivan
 
Lubrication Neglect Causes More Downtime Than AI Ever Will Why Maintenance Fu...
byMaintWiz Technologies Private Limited
 

Overlap save method and overlap add method in dsp

  • 1.
    DIGITAL SIGNAL PROCESSING By Mrs.R.Chitra, AssistantProfessor(SS), Department of ECE, School of Engineering, Avinashilingam Institute for Home Science and Higher Education for Women, Coimbatore
  • 2.
    Topics to beCovered: 1. OVERLAP SAVE METHOD 2. OVERLAP ADD METHOD 3. LINEAR CONVOLUTION
  • 3.
    OVERLAP SAVE METHOD: Overlap–save is the traditional name for an efficient way to evaluate the discrete convolution between a very long signal x(n) and a finite impulse response FIR filter h(n)  In this method the input sequence is divided into blocks of data of size N=L+M-1.where L= length of an input sequence and M=the length of an impulse response  Each block consist of last (M-1) data points of previous block followed by L new data points to form a data sequence of length N=L+M-1.  For first block, M-1 points are set to zero. The input sequence can be divided into blocks as X1(n) = {0,0,x(0),x(1),x(2)} M-1=2zeros
  • 4.
    X2(n) = {x(1),x(2),x(3),x(4),x(5)} Lasttwo data points from previous block X3(n) = {x(4),x(5),x(6),x(7),x(8)} X4(n) = {x(7),x(8),x(9),x(10),x(11)} X5(n) = {x(10),x(11),x(12),x(13),x(14)} X6(n) = {x(13),x(14),0,0,0} Thus, Y1(n)=x1(n) h(n)={y1(0),y1(1),y1(2),y1(3),y1(4)} Y2(n)=x2(n) h(n)={y2(0),y2(1),y2(2),y2(3),y2(4)}N N
  • 5.
    Y3(n)=x3(n) h(n)={y3(0),y3(1),y3(2),y3(3),y3(4)} Y4(n)=x4(n) h(n)={y4(0),y4(1),y4(2),y4(3),y4(4)} Y5(n)=x5(n)h(n)={y5(0),y5(1),y5(2),y5(3),y5(4)} Y6(n)=x6(n) h(n)={y6(0),y6(1),y6(2),y6(3),y6(4)} Therefore, the output blocks are abutted together to get Y(n)={y1(2),y1(3),y1(4),y2(2),y2(3),y2(4),y3(2),y3(3), y3(4),y4(4),y5(2),y5(3),y5(4),y6(2),y6(3)} N N N N
  • 6.
    EXAMPLE 1: Determinethe output of linear FIR filter whose impulse response is h(n)={1,2,3} and the input signal is x(n)= {1,2,3,4,5,6,7,8,9} using over lap save method. SOLUTION: Given, x(n)= {1,2,3,4,5,6,7,8,9} & h(n)={1,2,3} Therefore, L=9;M=3; Adding M-1 zeros in x1(n),we get x1(n)={0,0,1,2,3} x2(n)={2,3,4,5,6} x3(n)={5,6,7,8,9} x4(n)={8,9,0,0,0} h(n)={1,2,3,0,0}
  • 7.
    By circular convolution, y1(n)=x1(n) h(n) y2(n)= x2(n) h(n) N N                                                  10 4 1 9 12 3 2 1 0 0 13300 01230 00123 30012 23001                                                  28 22 16 25 29 6 5 4 3 2 13300 01230 00123 30012 23001
  • 8.
    y3(n)= x3(n) h(n) y4(n)=x4(n) h(n) N N                                                  46 40 34 43 47 9 8 7 6 5 12300 01230 00123 30012 23001                                                  0 27 42 25 8 0 0 0 9 8 12300 01230 00123 30012 23001
  • 9.
    y(n)= Therefore, y(n)={1,4,10,16,22,28,34,40,46,42,27} 12 9 14 10 29 25 16 22 28 8 25 42 27 0 Add y3(n) y2(n) y1(n) 47 43 34 40 46 y4(n) Discard Discard Discard Discard
  • 10.
    EXAMPLE 2: Determinethe output of linear FIR filter whose impulse response is h(n)={1,-3,5} and the input signal is x(n)= {-1,4,7,3,-2,9,10,12,-5,8} using over lap save method. SOLUTION: Given, x(n)= {-1,4,7,3,-2,9,10,12,-5,8} & h(n)={1,-3,5} Therefore, L=9;M=3; Adding M-1 zeros in x1(n),we get x1(n)={0,0,-1,4,7} x2(n)={4,7,3,-2,9} x3(n)={-2,9,10,12,-5} x4(n)={12,-5,8,0,0} h(n)={1,-3,5,0,0}
  • 11.
    By circular convolution, y1(n)=x1(n) h(n) y2(n)= x2(n) h(n) N N                                                           10 7 1 35 1 7 4 1 0 0 13500 01350 00135 50013 35001                                                        30 24 2 40 33 9 2 3 7 4 13500 01350 00135 50013 35001
  • 12.
    y3(n)= x3(n) h(n) y4(n)=x4(n) h(n) N N                                                           9 27 27 10 73 5 12 10 9 2 13500 01350 00135 50013 35001                                                         40 49 83 0 1 0 0 8 5 12 13500 01350 00135 50013 35001
  • 13.
    y(n)= Therefore, y(n)={1,7,-10,2,24,30,-27,27,9,83,-49,40} -1 35 -17 -10 -33 40 2 24 30 1 0 83 -49 40 Add y3(n) y2(n) y1(n) 73 -10 -27 27 9 y4(n) Discard Discard Discard Discard
  • 14.
    OVERLAP ADD METHOD: The length of the sequence is be Ls and the length of the impulse response is M.  The sequence is divided into blocks of data size having length L and M-1.  Zeros are appended to it make the data size of L+M-1. Let the output blocks are of the form, y1(n)={y1(0),y1(1),…….,y1(L-1),y1(L),….,y1(N-1)} y2(n)={y2(0),y2(1),……,y2(L-1),y2(L),….,y2(N-1)} y3(n)={y3(0),y3(1),…….,y3(L-1),y3(L),……,y3(N-1)} the output sequence is Y(n)={y1(0),y1(1),….,y1(L-1),y1(L)+y2(0),….,y1(N-1)+ y2(M-2),y2(M),……,y2(L)+y3(0),y2(L+1)+y3(1),….,y3(N-1)}
  • 15.
    EXAMPLE 1: Determinethe output of linear FIR filter whose impulse response is h(n)={1,2,3} and the input signal is x(n)= {1,2,3,4,5,6,7,8,9} using over lap add method. SOLUTION: Given, x(n)= {1,2,3,4,5,6,7,8,9} & h(n)={1,2,3} Therefore, L=9;M=3; Adding M-1 zero,we get x1(n)={1,2,3,0,0} x2(n)={4,5,6,0,0} x3(n)={7,8,9,0,0} h(n)={1,2,3,0,0}
  • 16.
    By circular convolution, y1(n)=x1(n) h(n) y2(n)= x2(n) h(n) N N                                                  18 27 28 13 4 0 0 6 5 4 13300 01230 00123 30012 23001                                                  9 12 10 4 1 0 0 3 2 1 13300 01230 00123 30012 23001
  • 17.
  • 18.
    EXAMPLE 2: Determinethe output of linear FIR filter whose impulse response is h(n)={1,-3,5} and the input signal is x(n)= {-1,4,7,3,-2,9,10,12,-5,8} using over lap add method. SOLUTION: Given, x(n)= {-1,4,7,3,-2,9,10,12,-5,8} & h(n)={1,-3,5} Therefore, L=9;M=3; Adding M-1 zeros, we get x1(n)={-1,4,7,0,0} x2(n)={3,-2,9,0,0} x3(n)={10,12,-5,0,0} x4(n)={8,0,0,0,0} h(n)={1,-3,5,0,0}
  • 19.
    By circular convolution, y1(n)=x1(n) h(n) y2(n)= x2(n) h(n) N N                                                          45 37 30 11 3 0 0 9 2 3 13500 01350 00135 50013 35001                                                        35 1 10 7 1 0 0 7 4 1 13500 01350 00135 50013 35001
  • 20.
    y3(n)= x3(n) h(n) y4(n)=x4(n) h(n) N N                                                          25 75 9 18 10 0 0 5 12 10 13500 01350 00135 50013 35001                                                        0 0 40 24 8 0 0 0 0 8 13500 01350 00135 50013 35001
  • 21.
    y(n)= Therefore, y(n)={1,7,-10,2,24,30,-27,27,9,83,-49,40} 1 7 -10-1 35 3 -11 30 -37 45 8 -24 40 0 0 Add Add y3(n) y2(n) y1(n) 10 -18 9 75 -25 Add Add y4(n)
  • 22.
    LINEAR CONVOLUTION FROMCIRCULAR CONVOLUTION: • Let us consider two finite duration sequences x(n) and h(n). The duration of x(n) is L and y(n) is M samples. The linear convolution of x(n) and h(n) is given by the formula where y(n) is a finite duration of sequence of L+M-1 samples. The circular convolution of x(n) and h(n) give N samples where N=Max(L,M). Consider two sequences x(n) and h(n) having sequence length L=5 and M=3 respectively as shown in the figure. x(n) L=5 0 1 2 3 4     k knhkxny )()()(
  • 23.
    h(n) M=3 0 12 The linear convolution of x(n) and h(n) consist of 5+3-1=7 points. 3 3 3 y(n)=x(n)*h(n) 2 2 1 1 0 1 2 3 4 5 6 The circular convolution of x(n) and h(n) consist of 5 points short of M-1=2 points. Therefore the circular convolution will contain corrupted points due to time domain aliasing. These points are first (M-1) points as shown in the figure. Aliasing y(0)&y(5) y(1)&y(6) 0 1 2 3 4
  • 24.
  • 27.
  • 28.