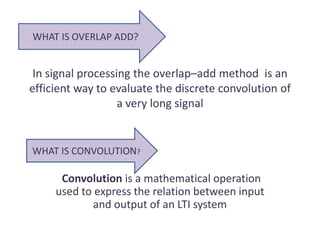
The overlap-add method is an efficient way to evaluate the discrete convolution of long signals using short blocks. It involves breaking the long signals into shorter blocks, zero-padding the blocks, convolving them, and adding the results. For example, an input signal of length N is broken into blocks of length M, with M-1 zeros added to each block. The blocks are convolved with the impulse response and added to produce the final output. This method was used to convolve an example input signal of length 10 with an impulse response of length 3.

1. OVERLAP-ADD METHOD
USING CONVOLUTION
GUIDED BY ASST.PROF PRAMOD KACHARE
PROJECT BY:
Megha Thakur- 17ET2004
Kiran Prashanth- 17ET2025
Anushka Pokle- 17ET1065
Aishwarya Zope- 17ET1016

2. CONTENTS:
2
1. What overlap add method ?
2. Steps to perform overlap add method.
3. Example of overlap add method.
4. Reference

3. 3
OVERLAP ADD
METHOD

4. In signal processing the overlap–add method is an
efficient way to evaluate the discrete convolution of
a very long signal
Convolution is a mathematical operation
used to express the relation between input
and output of an LTI system
WHAT IS OVERLAP ADD?
WHAT IS CONVOLUTION?

5. STEPS FOR OVERLAP ADD
METHOD
5
STEP-1:
Determine length ‘M’, which is the length of the
impulse response data sequences i.e. h[n] &
determine ‘M-1’.
STEP-2:
Given input sequence x[n] size is ‘N’. let assume,
N=5

6. 6
STEP-3:
Determine the length of the new data,
‘L’
STEP-4:
Pad ‘M-1’ zeros to xk[n]
Pad ‘L-1’ zeros to h[n]
xk[n] ‘M-1’ zeros
h[n] ‘L-1’ zeros

7. 7
Input Data Sequence x[n]
x1[n]
x2[n]
x4[n]
x3[n]
M-1 zeros
M-1 zeros
M-1 zeros
M-1 zeros
L L L L

8. 8
STEP-4:
Perform Convolution of h[n] & blocks of x[n]
i.e. y1[n]= x1[n]
y2[n]= x2[n]
y3[n]= x3[n]
y4[n]= x4[n]
N
N
h[n]
h[n]
N h[n]
h[n]
N

9. 9
y1[n]
y2[n]
y4[n]
y3[n]
M-1 data
M-1 data
M-1 data
Final Output Data Sequence y[n]
M-1 data
add
add
add

10. 10
& h[n]={1,1,1}Ques. Given x[n]={3,-1,0,1,3,2,0,1,2,1}
 Let, N=5
Length of h[n], M= 3
Therefore, M-1= 2
We know,
 N=(L+M-1)
 5=L+3-1
 L=3
∴Pad L-1=2 zeros with h[n] i.e. h[n]={1,1,1,0,0}
SOLVED EXAMPLE

11. 11
3 -1 0 1 3 2 0 1 2 1
0 1 2
x2[n]
x4[n]
x3[n]
M-1(=2) no. of zeros
L(=3) no. of new data
3 -1 0 0 0
1 3 2 0 0
Input sequence x[n]
x1[n]
1 0 0 0 0
0 0

12. 12
Performing yk[n]= xk[n] h[n], where k=1,2,3,4
1. y1[n]=
2. y2[n]=
3. y3[n]=
4. y4[n]=
{3,2,2,-1,0}
{1,4,6,5,2}
{0,1,3,3,2}
{1,1,1,0,0}
N

13. 1 4 6 5 2
0 1
1 1 1 0 0
+=> add
n- 0 1 2 3 4 5 6 7 8 9 10 11 12 13
y1[n]
y1[n]
y1[n]
y1[n]
3 2 2 -1 0
+ +
++
3 3 2
+ +
y[n] 3 2 2
30

14. 1 4 6 5 2
0 1
1 1 1 0 0
+=> add
n- 0 1 2 3 4 5 6 7 8 9 10 11 12 13
y1[n]
y1[n]
y1[n]
y1[n]
3 2 2 -1 0
+ +
++
3 3 2
+ +
y[n] 3 2 2 0 4 6
31

15. 1 4 6 5 2
0 1
1 1 1 0 0
+=> add
n- 0 1 2 3 4 5 6 7 8 9 10 11 12 13
y1[n]
y1[n]
y1[n]
y1[n]
3 2 2 -1 0
+ +
++
3 3 2
+ +
y[n] 3 2 2 0 4 6 5 3 3
32

16. 1 4 6 5 2
0 1
1 1 1 0 0
+=> add
n- 0 1 2 3 4 5 6 7 8 9 10 11 12 13
y1[n]
y1[n]
y1[n]
y1[n]
3 2 2 -1 0
+ +
++
3 3 2
+ +
y[n] 3 2 2 0 4 6 5 3 3 4 3
33

17. 1 4 6 5 2
0 1
1 1 1 0 0
+=> add
n- 0 1 2 3 4 5 6 7 8 9 10 11 12 13
y1[n]
y1[n]
y1[n]
y1[n]
3 2 2 -1 0
+ +
++
3 3 2
+ +
y[n] 3 2 2 0 4 6 5 3 3 4 3 1 0 0
34

18. 1 4 6 5 2
0 1
1 1 1 0 0
+=> add
n- 0 1 2 3 4 5 6 7 8 9 10 11 12 13
y1[n]
y1[n]
y1[n]
y1[n]
3 2 2 -1 0
+ +
++
3 3 2
+ +
y[n] 3 2 2 0 4 6 5 3 3 4 3 1 0 0
35

19. REFERENCE:
19
 Digital Signal Processing - P. Rameshbabu
 Discrete Time Signal Processing - Oppenheim & Schafer