The document discusses complementarity in quantum error correction and quantum cryptography. It begins with an introduction and outline. It then covers the Stinespring dilation theorem, purification of mixed states, conjugate/complementary channels, private quantum codes including for single qubits, and the complementarity of quantum codes. An example is also provided to illustrate complementarity between a swap channel and its conjugate.

1. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
On Complementarity In QEC
And Quantum Cryptography
David Kribs
Professor & Chair
Department of Mathematics & Statistics
University of Guelph
Associate Member
Institute for Quantum Computing
University of Waterloo
QEC II — USC — December 2011

2. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Outline
1 Introduction
Notation
2 Stinespring Dilation Theorem
Heisenberg & Schr¨dinger Pictures
o
Purification of Mixed States
Conjugate/Complementary Channels
3 Private Quantum Codes
Definition
Single Qubit Private Channels
4 Connection with QEC and Beyond
Complementarity of Quantum Codes
From QEC to QCrypto?
5 Conclusion
Summary

3. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Notation
HA , HB will denote Hilbert spaces for systems A and B.
B(H) will denote the set of (bounded) linear operators on H;
B(H)t will denote the trace class operators on H. In finite
dimensions these sets coincide and so we’ll simply write L(H)
B(HA , HB ) will denote the set of linear transformations from
HA to HB .
We’ll write X , Y for operators in B(H), and ρ, σ for density
operators in B(H)t . (And we’ll just refer to L(H) when
appropriate.)
Given a linear map Φ : B(HA )t → B(HB )t , its dual map
Φ† : B(HB ) → B(HA ) is defined via the Hilbert-Schmidt inner
product: Tr(ρ Φ† (X )) = Tr(Φ(ρ)X ).

4. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Heisenberg Picture
Suppose that Φ† : B(HB ) → B(HA ) is a completely positive
(CP) unital (Φ† (IB ) = IA ) linear map.

5. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Heisenberg Picture
Suppose that Φ† : B(HB ) → B(HA ) is a completely positive
(CP) unital (Φ† (IB ) = IA ) linear map.
Then there is a Hilbert space K (of dimension at most
dim(A) dim(B)) and a co-isometry V ∈ B(HB ⊗ K, HA )
(VV † = IA ) such that
Φ† (X ) = V (X ⊗ IK )V † ∀X .

6. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Heisenberg Picture
Suppose that Φ† : B(HB ) → B(HA ) is a completely positive
(CP) unital (Φ† (IB ) = IA ) linear map.
Then there is a Hilbert space K (of dimension at most
dim(A) dim(B)) and a co-isometry V ∈ B(HB ⊗ K, HA )
(VV † = IA ) such that
Φ† (X ) = V (X ⊗ IK )V † ∀X .
V is unique up to a unitary on K. Here the Kraus operators
for Φ† can be read off as the “coordinate operators” of V † :
 †
V1
†  . 
V = .  .
†
VAB

7. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Schr¨dinger Picture
o
Suppose that Φ : B(HA )t → B(HB )t is a CP trace preserving
(CPTP) linear map.

8. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Schr¨dinger Picture
o
Suppose that Φ : B(HA )t → B(HB )t is a CP trace preserving
(CPTP) linear map.
Then there is a Hilbert space K (of dimension at most
dim(A) dim(B)), an isometry U ∈ B(HA ⊗ K, HB ⊗ K), and a
pure state |ψ ∈ K such that
Φ(ρ) = TrK (U(ρ ⊗ |ψ ψ|)U † ) ∀ρ.

9. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Schr¨dinger Picture
o
Suppose that Φ : B(HA )t → B(HB )t is a CP trace preserving
(CPTP) linear map.
Then there is a Hilbert space K (of dimension at most
dim(A) dim(B)), an isometry U ∈ B(HA ⊗ K, HB ⊗ K), and a
pure state |ψ ∈ K such that
Φ(ρ) = TrK (U(ρ ⊗ |ψ ψ|)U † ) ∀ρ.
The two pictures are connected via V † |φ := U(|φ ⊗ |ψ ),
which gives Φ(ρ) = TrK (V † ρV ).

10. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Schr¨dinger Picture
o
Suppose that Φ : B(HA )t → B(HB )t is a CP trace preserving
(CPTP) linear map.
Then there is a Hilbert space K (of dimension at most
dim(A) dim(B)), an isometry U ∈ B(HA ⊗ K, HB ⊗ K), and a
pure state |ψ ∈ K such that
Φ(ρ) = TrK (U(ρ ⊗ |ψ ψ|)U † ) ∀ρ.
The two pictures are connected via V † |φ := U(|φ ⊗ |ψ ),
which gives Φ(ρ) = TrK (V † ρV ).
The Kraus operators for Φ are the coordinate operators Vi
from above, and the general form for U is
U = V† ∗

11. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Purification of Mixed States
Fix a density operator ρ0 ∈ B(H)t , and consider the CPTP
map Φ : C → B(H)t defined by
Φ(c · 1) = c ρ0 ∀c ∈ C.

12. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Purification of Mixed States
Fix a density operator ρ0 ∈ B(H)t , and consider the CPTP
map Φ : C → B(H)t defined by
Φ(c · 1) = c ρ0 ∀c ∈ C.
Then the Stinespring Theorem gives (here K = C ⊗ H = H):
ρ0 = Φ(1) = TrK (U(1 ⊗ |ψ ψ|)U † ) = TrK (|ψ ψ |),
where |ψ ∈ H ⊗ H is a purification of ρ0 – and the unitary
freedom in the theorem captures all purifications.

13. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Conjugate/Complementary Channels
Definition
(King, et al.; Holevo) Given a CPTP map Φ : L(HA ) → L(HB ),
consider V ∈ L(HB ⊗ K, HA ) and K above for which
Φ(ρ) = TrK (V † ρV ).
Then the corresponding conjugate (or complementary) channel
is the CPTP map Φ : L(HA ) → L(K) given by
Φ(ρ) = TrB (V † ρV ).
Fact: Any two conjugates Φ, Φ obtained in this way are related
by a partial isometry W such that Φ(·) = W Φ (·)W † . We talk of
“the” conjugate channel for Φ with this understanding.

14. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Computing Kraus Operators for Conjugates
Suppose that Vi ∈ L(HA , HB ) are the Kraus operators for
Φ : L(HA ) → L(HB ). Then we can obtain Kraus operators
{Rµ } for Φ as follows.

15. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Computing Kraus Operators for Conjugates
Suppose that Vi ∈ L(HA , HB ) are the Kraus operators for
Φ : L(HA ) → L(HB ). Then we can obtain Kraus operators
{Rµ } for Φ as follows.
Fix a basis {|ei } for K and define for ρ ∈ L(HA ),
F (ρ) = |ei ej | ⊗ Vi ρVi† ∈ L(K ⊗ HB ).
i,j

16. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Computing Kraus Operators for Conjugates
Suppose that Vi ∈ L(HA , HB ) are the Kraus operators for
Φ : L(HA ) → L(HB ). Then we can obtain Kraus operators
{Rµ } for Φ as follows.
Fix a basis {|ei } for K and define for ρ ∈ L(HA ),
F (ρ) = |ei ej | ⊗ Vi ρVi† ∈ L(K ⊗ HB ).
i,j
Then Φ(ρ) = TrK F (ρ) and
Φ(ρ) = TrB F (ρ) = Tr(Vi ρVj† )|ei ej | = †
Rµ ρRµ ,
i,j µ
† † †
where Rµ = [V1 |fµ V2 |fµ · · · ] and {|fµ } is a basis for HB .

17. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Private Quantum Codes
Definition
(Ambainis, et al.) Let S ⊆ H be a set of pure states, let
Φ : L(HA ) → L(HB ) be a CPTP map, and let ρ0 ∈ L(H). Then
[S, Φ, ρ0 ] is a private quantum channel if we have
Φ(|ψ ψ|) = ρ0 ∀|ψ ∈ S.
Motivating class of examples: random unitary channels, where
Φ(ρ) = i pi Ui ρUi† .

18. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Single Qubit Private Codes
Recall a single qubit pure state |ψ can be written
θ 1 θ 0
|ψ = cos + e iϕ sin .
2 0 2 1
We associate |ψ with the point (θ, ϕ), in spherical coordinates, on
θ θ
the Bloch sphere via α = cos 2 and β = e iϕ sin 2 . The
associated Bloch vector is r = (cos ϕ sin θ, sin ϕ sin θ, cos θ).
Using the Bloch sphere representation, we can associate to any
single qubit density operator ρ a Bloch vector r ∈ R3 satisfying
r ≤ 1, where
I +r ·σ
ρ= .
2
We use σ to denote the Pauli vector; that is, σ = (σx , σy , σz )T .

19. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Single Qubit Private Codes
Every unital qubit channel Φ can be represented as
1 1
Φ [I + r · σ] = [I + (T r ) · σ] ,
2 2
where T is a 3 × 3 real matrix that represents a deformation of the
Bloch sphere.
We are interested in cases where S is nonempty. So we consider
the cases in which T has non-trivial nullspace; that is, the subspace
of vectors r such that T r = 0 is one, two, or three-dimensional.

20. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Single Qubit Private Codes
Theorem
Let Φ : M2 → M2 be a unital qubit channel, with T the mapping
induced by Φ as above. Then there are three possibilities for a
private quantum channel [S, Φ, 1 I ] with S nonempty:
2
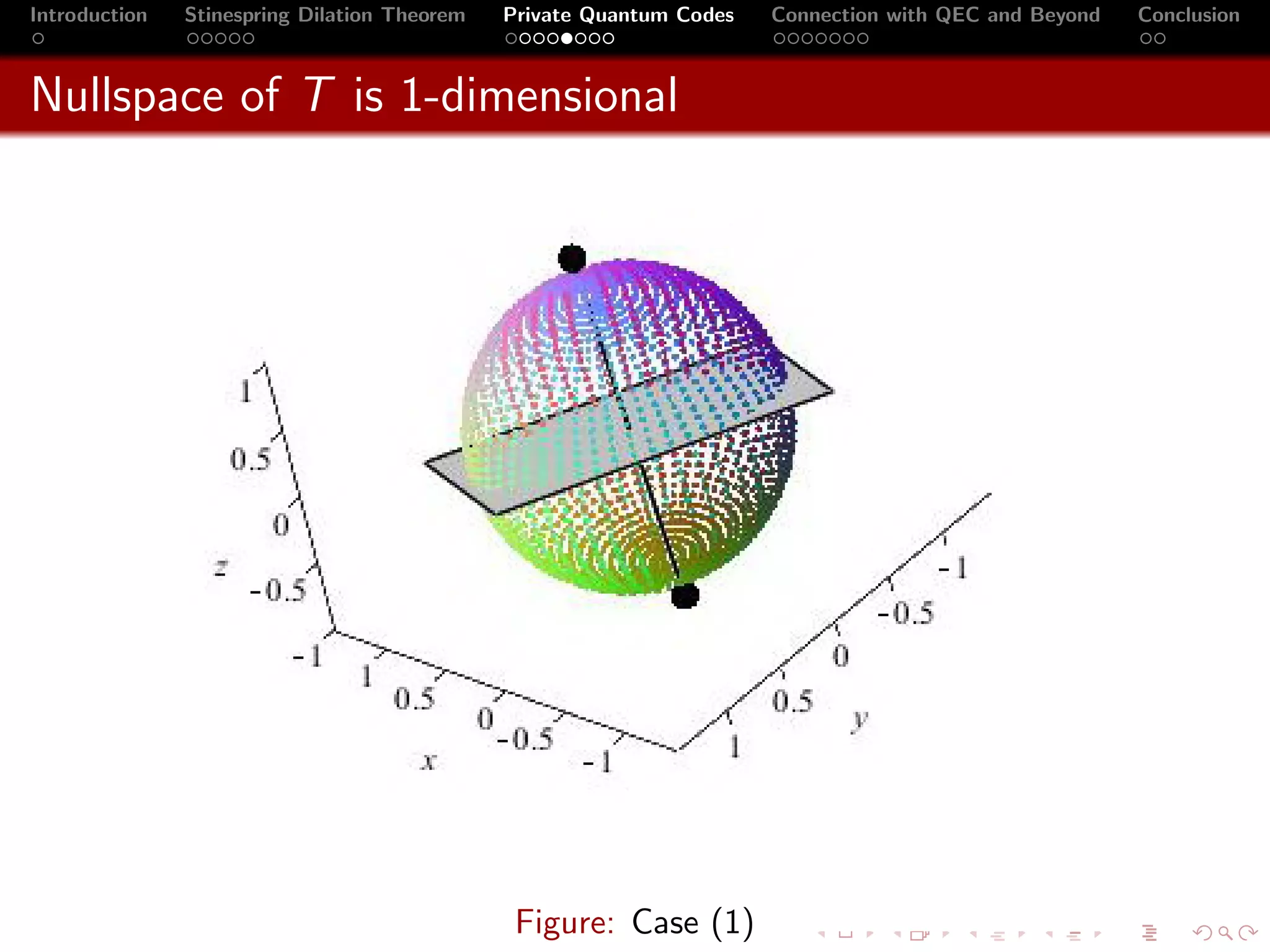
1 If the nullspace of T is 1-dimensional, then S consists of a
pair of orthonormal states.
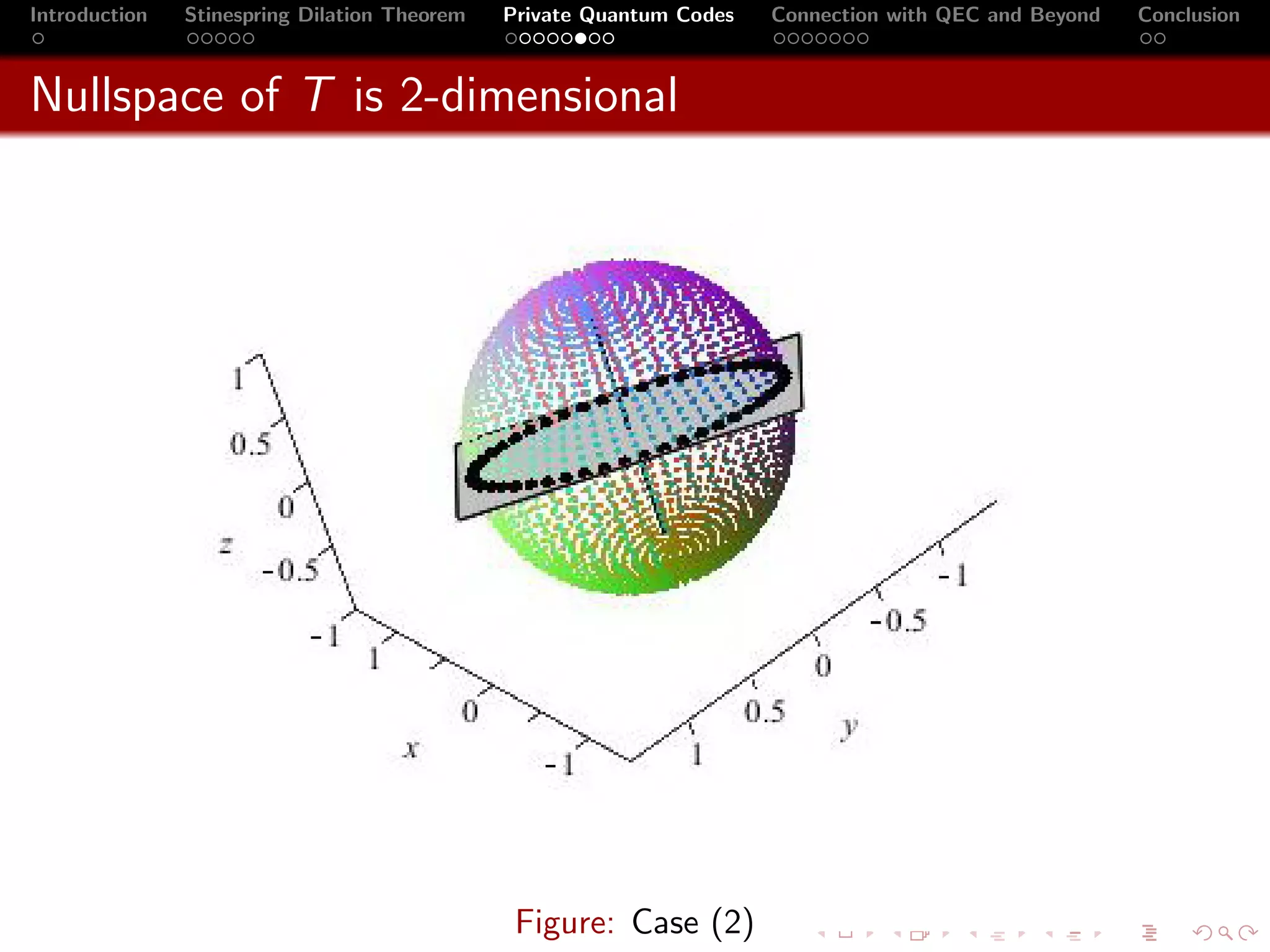
2 If the nullspace of T is 2-dimensional, then the set S is the
set of all trace vectors (see below) of the subalgebra U † ∆2 U
of 2 × 2 diagonal matrices up to a unitary equivalence.
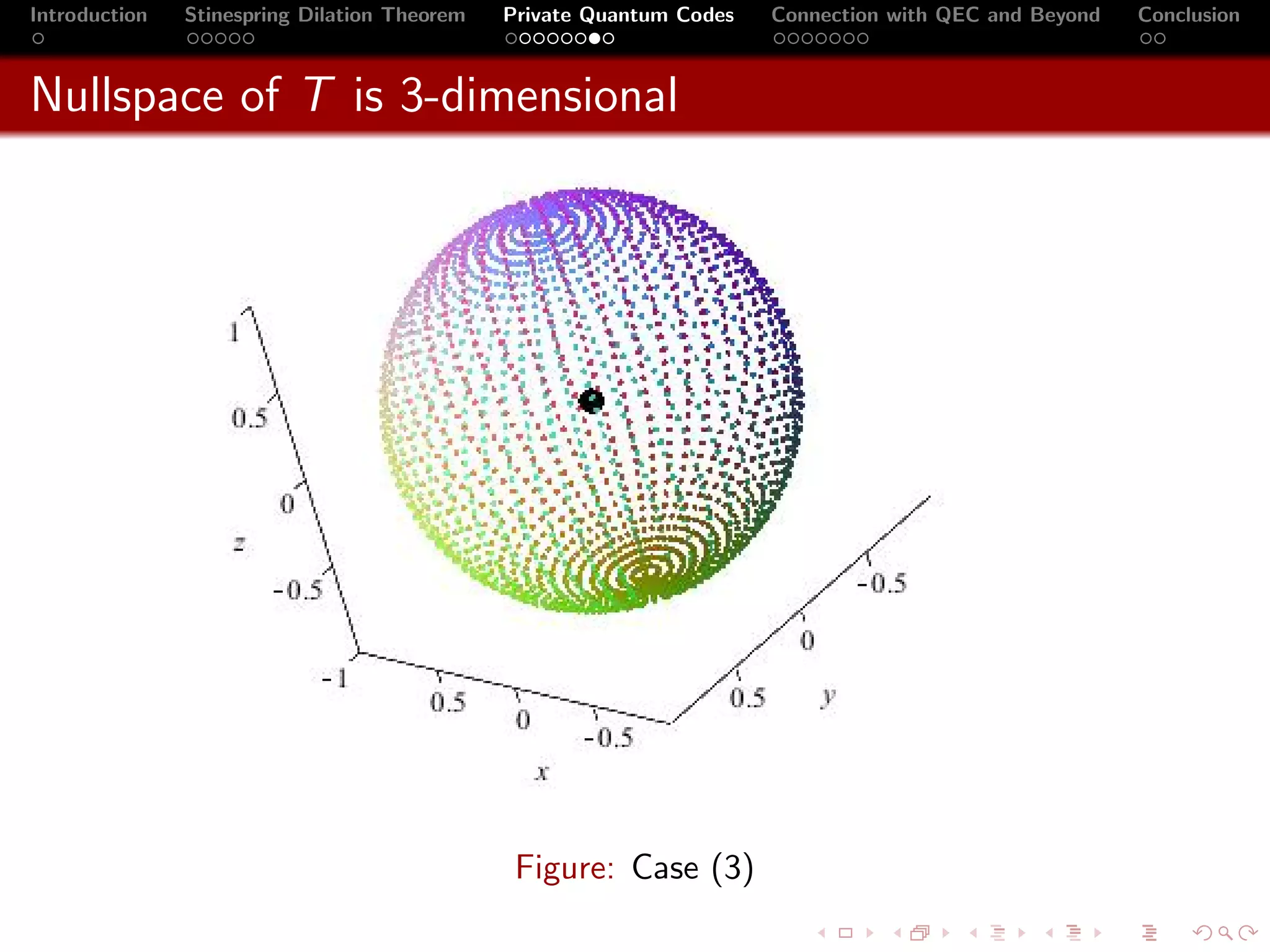
3 If the nullspace of T is 3-dimensional, then Φ is the
completely depolarizing channel and S is the set of all unit
vectors. In other words, S is the set of all trace vectors of
C · I2 .

21. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Nullspace of T is 1-dimensional
Figure: Case (1)

22. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Nullspace of T is 2-dimensional
Figure: Case (2)

23. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Nullspace of T is 3-dimensional
Figure: Case (3)

24. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Private Code Side-Bar
Note: There are interesting connections between private quantum
codes and the notions of conditional expectations and trace vectors
in the theory of operator algebras – maybe as far back as eighty
years ago. For more on this see:
A. Church, D.W. Kribs, R. Pereira, S. Plosker, Private Quantum
Channels, Conditional Expectations, and Trace Vectors. Quantum
Information & Computation, 11 (2011), no. 9 & 10, 774 - 783.

25. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Complementarity of Quantum Codes
Theorem
(Kretschmann-K.-Spekkens) Given a conjugate pair of CPTP maps
Φ, Φ, a code is an error-correcting code for one if and only if it is a
private code for the other.
The extreme example of this phenomena is given by a unitary
channel paired with the completely depolarizing channel – where
the entire Hilbert space is the code.

26. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Example 4.1
Consider the 2-qubit swap channel Φ(σ ⊗ ρ) = ρ ⊗ σ, which
has a single Kraus operator, the swap unitary U.
The conjugate map Φ : L(C2 ⊗ C2 ) → C is implemented with
four Kraus operators, which are
R1 = 1 0 0 0
R2 = 0 0 1 0
R3 = 0 1 0 0
R4 = 0 0 0 1 ,
and one can easily see that Φ(ρ) = 1 for all ρ ∈ L(C2 ).

27. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Example 4.2
Consider the 2-qubit phase flip channel Φ with (equally weighted)
Kraus operators {I , Z1 }. The dilation Hilbert space here is 3-qubits
in size, and the conjugate channel Φ : L(C2 ⊗ C2 ) → L(C2 ) is
implemented with the following Kraus operators:
1 1 0 0 0 1 0 1 0 0
R1 = √ R2 = √
2 1 0 0 0 2 0 1 0 0
1 0 0 1 0 1 0 0 0 1
R3 = √ R4 = √
2 0 0 −1 0 2 0 0 0 −1

28. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Example 4.2
4 †
We have Φ(ρ) = 1 (ρ + Z1 ρZ1 ) and Φ(ρ) =
2 i=1 Ri ρRi for
all 2-qubit ρ.
It is clear that the code {|00 , |01 } is correctable for Φ; in
fact it is noiseless/decoherence-free. And thus we know it is
private for the conjugate channel Φ.
Indeed, one can check directly that every density operator ρ
supported on {|00 , |01 }, satisfies
1
Φ(ρ) = |+ +| = (|0 + |1 )( 0| + 1|).
2

29. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
From QEC to QCrypto?
General Program: Using the “algebraic bridge” given by the
notion of conjugate channels, investigate what results, techniques,
special types of codes, applications, etc, etc, from QEC have
analogues or versions in the world of private quantum codes and
quantum cryptography. At the least, we can use work from QEC as
motivation for studies in this different setting...

30. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
“Knill-Laflamme” Type Conditions for Private Codes
Theorem
(K.-Plosker) A projection P is a private code for a CPTP map Φ
with output state ρ0 ; i.e., Φ(ρ) = ρ0 for all ρ ∈ L(PH)
if and only if
∀X ∃λX ∈ C : PΦ† (X )P = λX P.
In this case, λX = Tr(ρ0 X ).

31. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
“Knill-Laflamme” Type Conditions for Private Codes
QEC Motivation: If P is correctable for Φ then ∃λµν ∈ C
†
such that PRµ Rν P = λµν P. But
PRµ Rν P = PΦ† (|fµ fν |)P.
†
Consequence: For instance in the case that
ρ0 ∝ Q = k |ψk ψk | and P = l |φl φl |, it follows that
there are scalars uikl such that for all i
1
Vi P = uikl Akl where Akl = |ψk φl |.
k,l
rank(Q)

32. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
Conclusion
The Stinespring Dilation Theorem is a foundational
mathematical result for quantum information, and it naturally
gives rise to the notion of conjugate channels.
Private quantum codes are a basic tool in quantum
cryptography, and can also be viewed from an operator
theoretic perspective.
Quantum error correcting codes are complementary to private
quantum codes, with conjugate channels providing a clean
algebraic bridge between the two studies.
It should be possible to develop analogues of many results,
techniques, applications, etc, from QEC for use in quantum
cryptography. We have discussed some here, but there seem
to be many other natural questions...

33. Introduction Stinespring Dilation Theorem Private Quantum Codes Connection with QEC and Beyond Conclusion
THANK YOU !