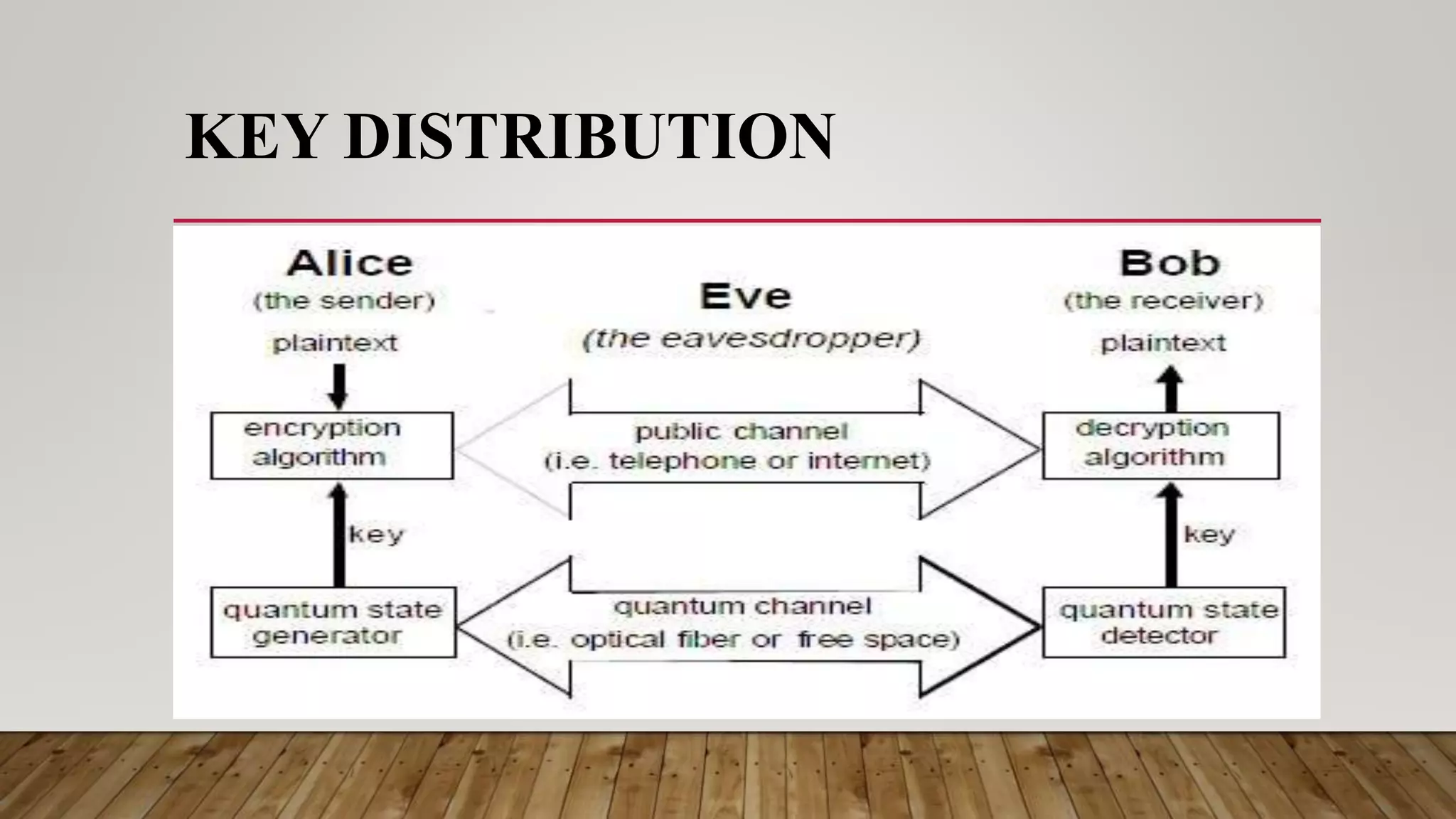
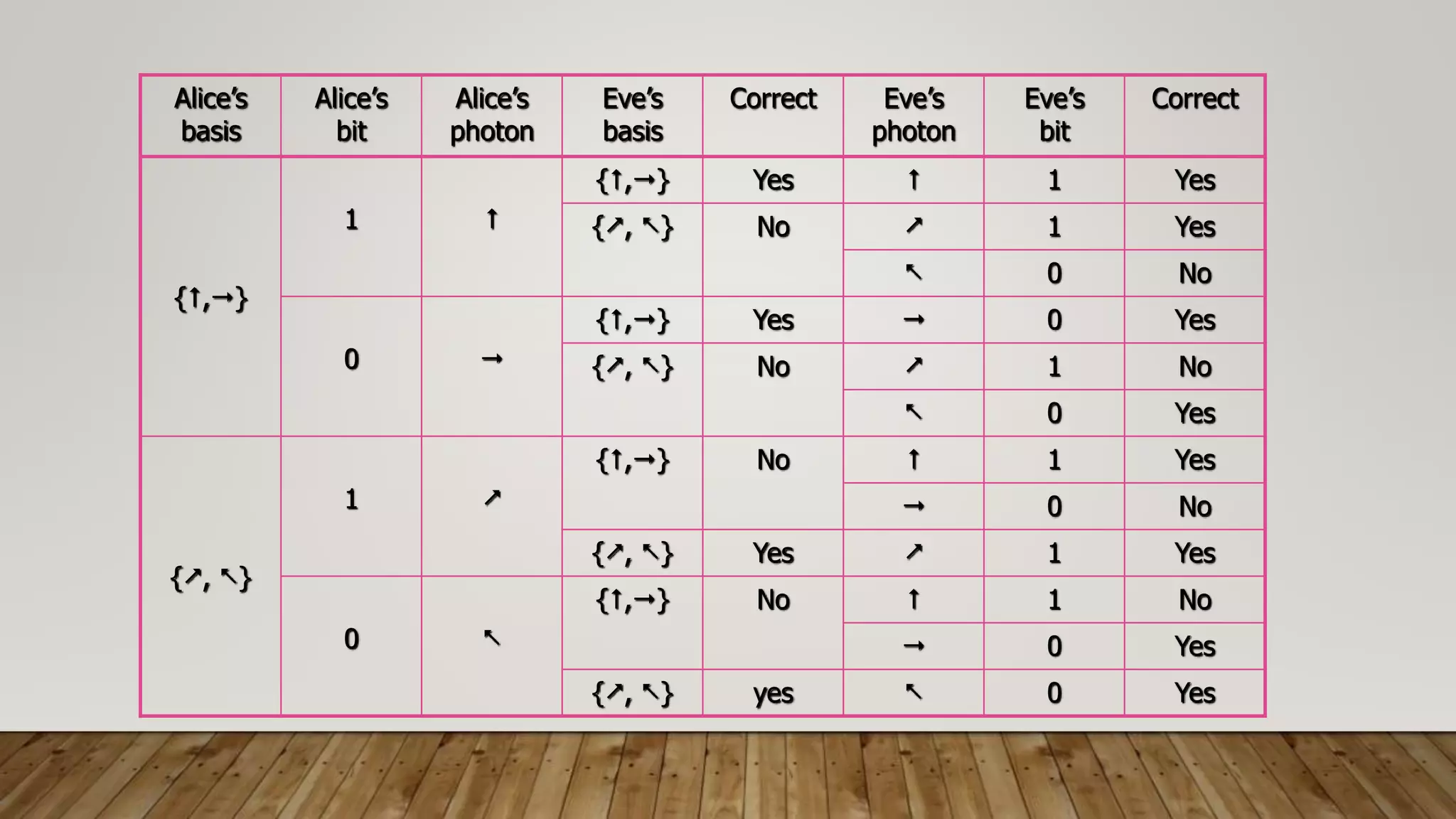
This document discusses the principles and history of quantum cryptography. It explains that quantum cryptography uses the Heisenberg uncertainty principle and quantum entanglement to securely transmit encryption keys. It outlines the key distribution process where Alice and Bob send polarized photons in random bases and later reveal the bases to determine the shared key. The document also discusses how an eavesdropper like Eve would not be able to intercept the photons without introducing errors, and how Alice and Bob can detect errors during transmission.

1. Introduction
 Quantum Cryptography is an effort to allow two users of a common communication channel
to create a body of shared and secret information. This information, which generally takes the
form of a random string of bits, can then be used as a conventional secret key for secure
communication.
 The Heisenberg Uncertainty principle and quantum entanglement can be exploited in as
system of secure communication often referred to as “quantum Cryptography”.

2. Heisenberg uncertainty principle : states that certain pairs of physical
properties are related in such a way that measuring one property
prevents the observer from simultaneously knowing the value for other.
Principle of photon polarization: tells that an eavesdropper cannot copy
unknown Qubits due to non-cloning algorithm.
 Photon :--It is the elementary particle responsible for
electromagnetic phenomena. It is the carrier of electromagnetic
radiations.
 Quantum entanglement :--It is a physical resource like energy. It can
be measured, transformed and purified.

3. History
In the early 1970 Stephen Wiesner, firstly introduced the concept of
quantum conjugate coding in New York.
His seminal paper titled "Conjugate Coding" was rejected by IEEE
Information Theory but was eventually published in 1983 in SIGACT
News (15:1 pp. 78-88, 1983).
A decade later, Charles H. Bennett, of the IBM Thomas J. Watson
Research Center, and Gilles Brassard, of the Université de Montréal,
proposed a method for secure communication based on Wiesner’s
“conjugate observables”.
In 1990, Artur Ekert, then a Ph.D. student of Oxford University,
developed a different approach to quantum cryptography known as
quantum entanglement.

4.  Classical Cryptography relies heavily on the complexity of factoring
integers.
 Quantum Computers can use Shor’s Algorithm to efficiently break
today’s cryptosystems.
 We need a new kind of cryptography!
Need of Quantum Cryptography

5. KEY DISTRIBUTION
Alice and Bob first agree on two representations for
ones and zeroes
One for each basis used, {,}
and {, }.
This agreement can be done in public
Define
1 =  0 = 
1 =  0 = 

6. KEY DISTRIBUTION

7. KEY DISTRIBUTION
Alice sends a sequence of photons to Bob.
Each photon in a state with polarization corresponding to 1 or 0, but with
randomly chosen basis.
Bob measures the state of the photons he receives, with each state measured
with respect to randomly chosen basis.
Alice and Bob communicates via an open channel. For each photon, they reveal
which basis was used for encoding and decoding respectively. All photons which
has been encoded and decoded with the same basis are kept, while all those
where the basis don't agree are discarded

8. EAVESDROPPING
Eve has to randomly select basis for her measurement
Her basis will be wrong in 50% of the time.
Whatever basis Eve chose she will measure 1 or 0
When Eve picks the wrong basis, there is 50% chance that she'll measure the right
value of the bit
E.g. Alice sends a photon with state corresponding to 1 in the {,}
basis. Eve picks the {, } basis for her measurement which this time happens to
give a 1 as result, which is correct.

9. EXAMPLE OF KEY DISTRIBUTION

10. Alice’s
basis
Alice’s
bit
Alice’s
photon
Eve’s
basis
Correct Eve’s
photon
Eve’s
bit
Correct
{,}
1 
{,} Yes  1 Yes
{, } No  1 Yes
 0 No
0 
{,} Yes  0 Yes
{, } No  1 No
 0 Yes
{, }
1 
{,} No  1 Yes
 0 No
{, } Yes  1 Yes
0 
{,} No  1 No
 0 Yes
{, } yes  0 Yes

11. EVES PROBLEM
Eve has to re-send all the photons to Bob
Will introduce an error, since Eve don't know the correct basis used
by Alice
Bob will detect an increased error rate
Still possible for Eve to eavesdrop just a few photons, and hope that
this will not increase the error to an alarming rate. If so, Eve would
have at least partial knowledge of the key.

12. NOISE
Noise might introduce errors
A detector might detect a photon even though there are no photons
Solution:
 Send the photons according to a time schedule.
 Then Bob knows when to expect a photon, and can discard those that
doesn't fit into the scheme's time window.
There also has to be some kind of error correction in the over all process.

13. ERROR CORRECTION
Alice and Bob agree on a random permutation of the bits in the key
They split the key into blocks of length k
Compare the parity of each block. If they compute the same parity, the block
is considered correct. If their parity is different, they look for the erroneous bit,
using a binary search in the block. Alice and Bob discard the last bit of each
block whose parity has been announced
This is repeated with different permutations and block size, until Alice and
Bob fail to find any disagreement in many subsequent comparisons

14. ATTACKS
• In Quantum Cryptography, traditional man-in-the-middle
attacks are impossible due to the Observer Effect.
• If Alice and Bob are using an entangled photon system, then it
is virtually impossible to hijack these, because creating three
entangled photons would decrease the strength of each
photon to such a degree that it would be easily detected.

15. ADVANTAGES:
 The biggest advantage of public key cryptography is the
secure nature of the private key. In fact, it never needs to be
transmitted or revealed to anyone.
It enables the use of digital certificates and digital timestamps,
which is a very secure technique of signature authorization.

16. DISADVANTAGES:
Transmission time for documents encrypted using public key
cryptography are significantly slower then symmetric
cryptography. In fact, transmission of very large documents is
prohibitive.
The key sizes must be significantly larger than symmetric
cryptography to achieve the same level of protection.

17. CONCLUSION
Quantum cryptography is a major achievement in security
engineering.
As it gets implemented, it will allow perfectly secure bank
transactions, secret discussions for government officials, and
well-guarded trade secrets for industry!