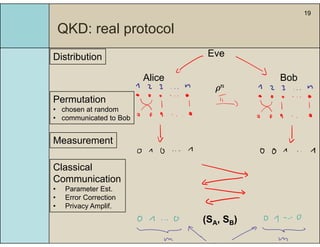
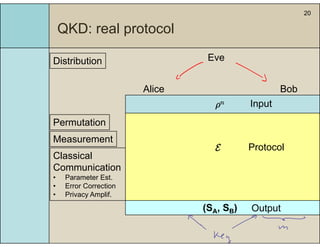
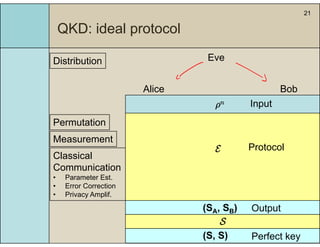
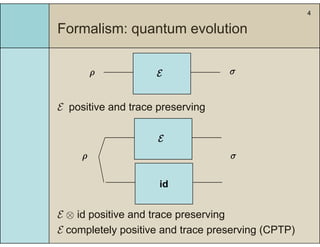
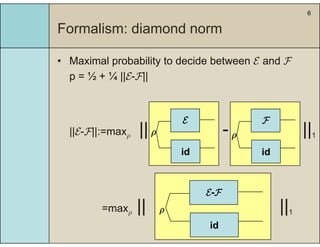
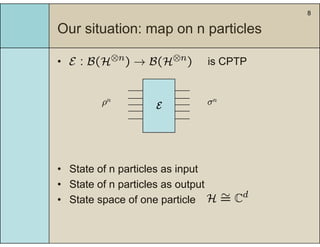
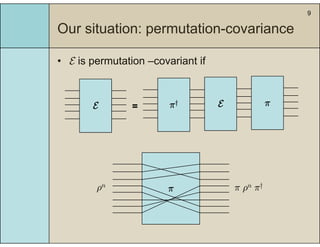
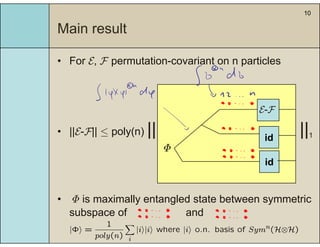
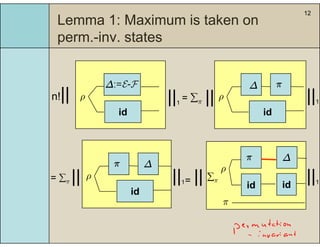
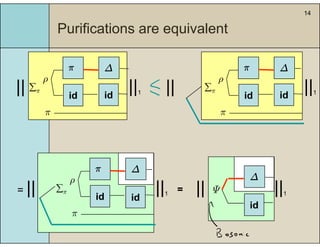
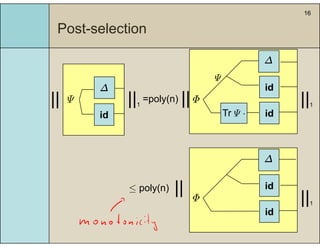
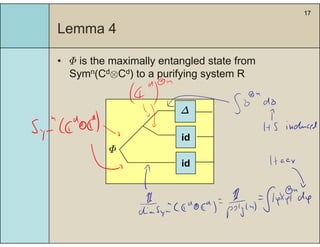
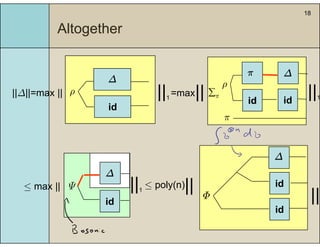
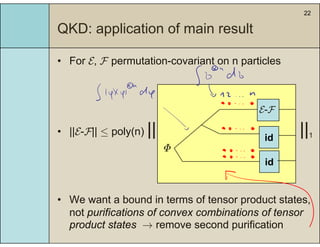
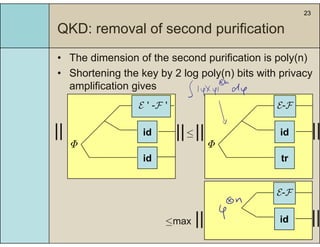
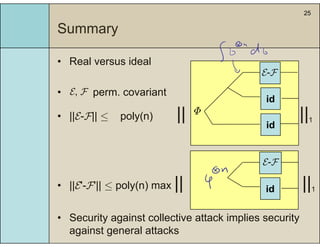
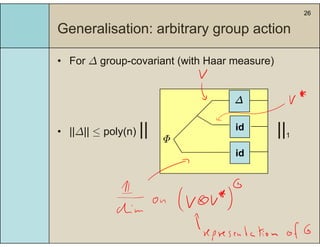
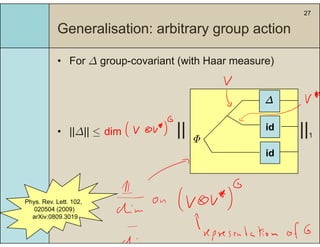
1) The document presents a technique for analyzing the security of real quantum key distribution (QKD) protocols by comparing them to an ideal protocol. 2) It introduces a formalism using completely positive and trace preserving maps and the diamond norm to measure the distance between real and ideal processes. 3) The main result is that for quantum evolutions that are permutation covariant, the diamond norm between them is bounded by a polynomial in the number of particles, when compared to evolutions corresponding to maximally entangled states. 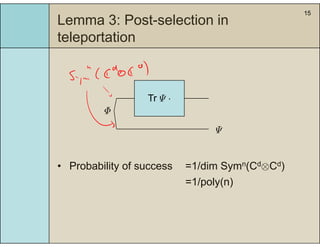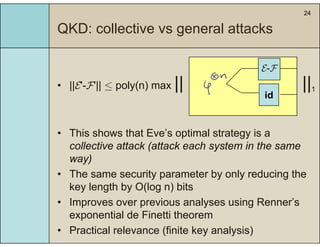4) This bound allows proving the security of QKD protocols against general attacks by showing they are secure against collective attacks, improving on previous analyses that relied on an exponential de Finetti theorem.

1. Postselection technique for quantum
channels with application to QKDchannels with application to QKD
Matthias Christandl, University of Munich
joint with Robert König and Renato Renner

2. 2
Outline
• MotivationMotivation
• FormalismFormalism
• Main Result• Main Result
• Proof• Proof
• Application to Quantum Cryptography• Application to Quantum Cryptography
Summary and Extension• Summary and Extension

3. 3
Motivation: real versus ideal
• Car rideCar ride
– In the ideal car ride we have no accident
– In the real car ride we might have an accidentg
– We still take the car, if real ≈ ideal
• Quantum Key Distributiony
– In the ideal QKD scheme, Alice and Bob obtain
identical and perfectly secure strings (a key)
– In the real QKD scheme, Alice and Bob may obtain
non-identical and compromised strings
We still like to use QKD as long as real ≈ ideal– We still like to use QKD as long as real ≈ ideal
– Proving real ≈ ideal is a security proof
• Provide tool for comparing real and ideal processes• Provide tool for comparing real and ideal processes

4. 4
Formalism: quantum evolutionq
Eρ σ
E positive and trace preserving
E
ρ σ
id
E ⊗ id positive and trace preserving
id
E ⊗ id positive and trace preserving
E completely positive and trace preserving (CPTP)

5. 5
Formalism: quantum evolutionq
• Quantum Evolution
– completely positive and trace preserving (CPTP) map E
• Examples• Examples
– Quantum protocols (e.g. for QKD) (ideal or real)
– Quantum circuits
– Time evolution of a system with Hamiltonian H
– Car ride (ideal or real)
–– …
• Proving real ≈ ideal is done via proving that E ≈ F
– E and F are CPTP maps
• Need for distance measure on CPTP mapsNeed for distance measure on CPTP maps
– Diamond norm (Kitaev)

6. 6
Formalism: diamond norm
• Maximal probability to decide between E and FMaximal probability to decide between E and F
p = ½ + ¼ ||E-F||
|| ||
E F
||E-F||:=maxρ || - ||1
E
id
F
id
ρ ρ
id id
=maxρ || ||1
E-F
ρρ || ||1
id
ρ

7. 7
Formalism: diamond norm
• "If we cannot see a difference they are identical"If we cannot see a difference, they are identical
• Operational definition
• Strongest notion of distanceStrongest notion of distance
• Maximum is difficult to evaluate
• Diamond norm is related to completely bounded• Diamond norm is related to completely bounded
norm by duality

8. 8
Our situation: map on n particlesp p
• is CPTPE : B(H⊗n) → B(H⊗n) is CPTPE : B(H ) → B(H )
Eρn σn
• State of n particles as input
• State of n particles as output• State of n particles as output
• State space of one particle H ∼= Cd

9. 9
Our situation: permutation-covariancep
• E is permutation –covariant ifE is permutation covariant if
E = π† E π
†
πρn π ρn π†

10. 10
Main result
• For E, F permutation-covariant on n particlesFor E, F permutation covariant on n particles
|| ||
E-F
• ||E-F|| ≤ poly(n) || ||1
Φ
id
id
• Φ is maximally entangled state between symmetric
subspace of andsubspace of and
|Φi =
1
poly(n)
X
i
|ii|ii where |ii o.n. basis of Symn(H⊗H)

11. 11
Proof
• Lemma 1: The maximisation in the diamond norm isLemma 1: The maximisation in the diamond norm is
achieved on (purifications of) permutation-invariant
states
• Lemma 2: permutation-invariant states have
bosonic purifications
• Lemma 3: every bosonic state can be obtained by
post-selecting from a fixed state (with probability
1/ l ( ))1/poly(n))
f f f• Lemma 4: this fixed state is the purification of a de
Finetti state

12. 12
Lemma 1: Maximum is taken on
i t tperm.-inv. states
∆:=
!|| || || ||
π∆E-F
id
ρn!|| ||1
id
ρ|| ||1= π
ρ|| ||1
π ∆
= π || π
id
π ∆
id
||1=
ρ
id
|| ||1 || id id
π
||1

13. 13
Lemma 2: Permutation-invariant
t t h B i ifi tistates have Bosonic purifications
• ρ= π ρ π† for all πρ π ρ π for all π
• Define |Ψi = (ρ1/2⊗1) |Φi |Φi = |ii|ii
• ThenThen
π ⊗ π |Ψi = (π ⊗ π) (ρ1/2⊗1)|Φi
= (ρ1/2⊗1) (π ⊗ π) |Φi= (ρ ⊗1) (π ⊗ π) |Φi
= (ρ1/2⊗1) |Φi
= |Ψi= |Ψi
• Hence |Ψi is bosonic• Hence, |Ψi is bosonic
• |Ψi is also a purification of ρ

14. 14
Purifications are equivalentq
|| π
id
π ∆
id
||1
ρ
|| π
id
π ∆
id
||1
ρ
|| id id
π
||1 || id id
π
||1
||
∆
||||
π
||
ρ
∆
||
id
||1= Ψ= || π
id id
π
||1
ρ
π

15. 15
Lemma 3: Post-selection in
t l t titeleportation
Tr Ψ ·
Φ
Ψ
• Probability of success =1/dim Symn(Cd⊗Cd)
=1/poly(n)1/poly(n)

16. 16
Post-selection
∆
||
∆
||
Ψ
|| ||
id
||
id
||1
Ψ
Tr Ψ ·
||
id
||1
=poly(n) Φ
||
∆
id||≤ poly(n)
id
||1
Φ
id
id

17. 17
Lemma 4
• Φ is the maximally entangled state fromΦ is the maximally entangled state from
Symn(Cd⊗Cd) to a purifying system R
∆
Φ
id
id

18. 18
Altogetherg
∆
ρ || || 
π ∆
||
ρ
||∆||=max || =max
id
ρ ||1 || π
id id
π
||1
||∆||=max || =max
∆
∆
||Ψ ||≤ poly(n)
∆
id≤ ||
id
||1Ψ ||≤ poly(n)
id
||Φ
id≤ max ||

19. 19
QKD: real protocolQ p
EveDistribution
BobAlice
ρn
Permutation
• chosen at random
• communicated to Bob
Measurement
Classical
Communication
• Parameter Est.
• Error Correction
• Privacy Amplif.
(SA, SB)

20. 20
QKD: real protocolQ p
EveDistribution
BobAlice
Distribution
ρn Input
Permutation
Measurement
Cl i l
ProtocolE
Permutation
Classical
Communication
• Parameter Est.
E C ti• Error Correction
• Privacy Amplif.
(SA, SB) Output

21. 21
QKD: ideal protocolQ p
EveDistribution
BobAlice
Distribution
ρn Input
Permutation
Cl i l
ProtocolE
Measurement
Permutation
Classical
Communication
• Parameter Est.
E C ti• Error Correction
• Privacy Amplif.
(SA, SB) Output
S
(S, S) Perfect key

22. 22
QKD: application of main resultQ pp
• For E, F permutation-covariant on n particlesFor E, F permutation covariant on n particles
|| ||
E-F
• ||E-F|| ≤ poly(n) || ||1
Φ
id
id
• We want a bound in terms of tensor product states,
not purifications of convex combinations of tensornot purifications of convex combinations of tensor
product states → remove second purification

23. 23
QKD: removal of second purificationQ p
• The dimension of the second purification is poly(n)y( )
• Shortening the key by 2 log poly(n) bits with privacy
amplification gives
E-FE ' -F '
|| ||
Φ
id
Φ
id|| ||||||≤
trid
E-F
|||| id ||||≤max

24. 24
QKD: collective vs general attacksQ g
• ||E'-F'|| ≤ poly(n) max || ||1
E-F
idid
• This shows that Eve’s optimal strategy is a
collective attack (attack each system in the same
way)
• The same security parameter by only reducing the
k l th b O(l ) bitkey length by O(log n) bits
• Improves over previous analyses using Renner’s
exponential de Finetti theoremexponential de Finetti theorem
• Practical relevance (finite key analysis)

25. 25
Summaryy
• Real versus idealReal versus ideal
• perm covariant
E-F
E F perm. covariant
• ||E-F|| ≤ poly(n) || ||1
id
Φ
id
E, F
id
E-F
||E' F'|| ≤ poly(n) max || ||id• ||E'-F'|| ≤ poly(n) max || ||1
• Security against collective attack implies security
against general attacks

26. 26
Generalisation: arbitrary group actiony g p
• For ∆ group-covariant (with Haar measure)For ∆ group covariant (with Haar measure)
|| ||
∆
id• ||∆|| ≤ poly(n) || ||1
id
Φ
id
id

27. 27
Generalisation: arbitrary group actiony g p
• For ∆ group-covariant (with Haar measure)For ∆ group covariant (with Haar measure)
|| ||
∆
id• ||∆|| ≤ dim || ||1
id
Φ
id
id
Phys. Rev. Lett. 102,
020504 (2009)
arXiv:0809.3019