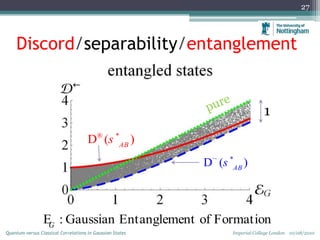
This document summarizes a talk on quantum versus classical correlations in Gaussian states. It discusses how quantum discord captures quantum correlations beyond entanglement, including in separable states. It introduces Gaussian quantum discord as a measure of quantum correlations for Gaussian states under Gaussian measurements. The key results are that all correlated Gaussian states have non-zero quantum correlations as measured by Gaussian discord, and Gaussian discord is limited for separable states but admits upper and lower bounds as a function of entanglement for entangled states. Open problems discussed include understanding quantum correlations in separable states and their operational interpretation.

1. Quantum versus Classical
Correlations in Gaussian States
Gerardo Adesso
joint work with Animesh Datta (Imperial College / Oxford)
School of Mathematical Sciences
Imperial College London 10/08/2010

2. Outline
• Quantum versus classical correlations
• Quantum discord
• Gaussian quantum discord
• Structure of Gaussian correlations
• Open problems
2
Quantum versus Classical Correlations in Gaussian States Imperial College London 10/08/2010

3. Correlations
3
Quantum versus Classical Correlations in Gaussian States Imperial College London 10/08/2010
A B
Classical correlations
Quantum correlations

4. Correlations
4
Quantum versus Classical Correlations in Gaussian States Imperial College London 10/08/2010
• Pure global composite states:
▫ entanglement = nonlocality
= nonclassicality (quantum correlations)
• Mixed global composite states:
▫ Werner 1989: separable = classically correlated
A B

5. Quantumness in separable states
Nonorthogonal separable states cannot be
discriminated exactly
Measuring a local observable on a separable
bipartite state will perturb the state
The eigenvectors of a separable state can be
entangled superpositions
…
In general separable states have not
a purely classical nature
5
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

6. A new paradigm
6
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
M. Piani, P. Horodecki, R. Horodecki, PRL 2008

7. Quantum discord
• A measure that strives at capturing all quantum correlations,
beyond entanglement, which can be nonzero also in separable states
• Introduced a decade ago in two independent works (Ollivier/Zurek
and Henderson/Vedral)
• Recently became very popular: stats from arXiv:quant-ph…
7
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
0
5
10
15
20
25
30
35
#preprints
year

8. Quantum discord
• Almost all bipartite states have nonzero quantum discord (purely
classically correlated states are of zero measure) A. Ferraro et al. PRA 2010
• Reduces to the entropy of entanglement on pure bipartite states
• Quantum discord without entanglement may allow for a
computational speed-up in the DQC1 model of quantum
computation A. Datta et al. 2008-2010; experiment: M. Barbieri et al. PRL 2008
8
discord
entanglement
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

9. Mutual information: classical
9
measuring total
correlations…
( )H A ( )H B
( : ) ( ) ( ) ( , )I A B H A H B H A B= + -
( : ) ( ) ( | )
( : ) ( ) ( | )
J A B H A H A B
J B A H B H B A
= -
= -
all equal
(Bayes’ rule)
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

10. what are these ??
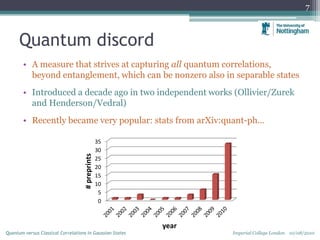
Mutual information: quantum
10
( )A
S ð ( )B
S ð
( ) ( ) ( ) ( )AB A B AB
I S S S= + -ð ð ð ð
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
( ) Tr[ log ]H S® = -ð ð ð
( ) ( ) ( | )
( ) ( ) ( | )
AB A
BA B
J S S A B
J S S B A
¬
®
= -
= -
ð ð
ð ð

11. Conditional entropy
11
( )A
S ð ( )B
S ð
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
• Introduce POVM on B:
• Posterior state of A after B
has been measured:
{ },B B
i i
i
P P =å 1
|
Tr [ ]
,
with r[ ]T
B
B i AB
A i
i
B
i i AB
p
p P=
P
=
ð
ð
ð
|
( | ) inf ( )B
i
i A i
i
S A B pS
P
º å ð• looking for the “least
disturbing measurement”:
( )AB
I ð

12. Bipartite correlations
• Total correlation
• One-way classical correlation Henderson, Vedral, JPA 2001
• Quantum discord Ollivier, Zurek, PRL 2001
12
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
( ) ( ) ( ) ( )AB A B AB
I S S S= + -ð ð ð ð
|
( ) ( ) ( | ) ( ) inf ( )B
i
AB A A i A i
i
S S A B S pS¬
P
= - = - åJ ^ð ð ð ð
|
( ) ( ) ( )
( ) ( ) inf ( )B
i
AB AB AB
B AB i A i
i
I
S S p S
¬ ¬
P
= -
= - + å
D ^ð ð J ^ð
ð ð ð
A B

13. Quantum discord
• For classical states (classical probability distribution embedded into
density matrices) I=J hence the quantum discord vanishes
• Zurek introduced it in the context of environment-induced
selection, identifying classical states with the pointer states
• The optimization involved in the conditional entropy is hard. Closed
analytical formulas are available only for special families of two-
qubit staes (X-shaped), not even for arbitrary states of two qubits
• Two recent independent works, including this one, defined a
Gaussian version of the quantum discord for bipartite Gaussian
states, where the optimization is restricted to Gaussian
measurements P. Giorda & M.G.A. Paris PRL 2010; GA & A. Datta PRL 2010
• We have solved the optimization problem and obtained a simple
formula for the Gaussian quantum discord of arbitrary two-mode
Gaussian states
13
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

14. Gaussian states
14
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
 Very natural: ground and thermal states of all physical systems in the
harmonic approximation regime (M.S.Kim: like orange juice and sunshine)
 Relevant theoretical testbeds for the study of structural properties of
entanglement and correlations, thanks to the symplectic formalism
 Preferred resources for experimental unconditional implementations of
continuous variable protocols
 Crucial role and remarkable control in quantum optics
- coherent states
- squeezed states
- thermal states

15. Gaussian operations
Gaussian states can be
efficiently:
 displaced
(classical currents)
 squeezed
(nonlinear crystals)
 rotated
(phase plates, beam splitters)
 measured
(homodyne detection)
15
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

16. Gaussian operations
Gaussian states can be
efficiently:
 displaced
(classical currents)
 squeezed
(nonlinear crystals)
 rotated
(phase plates, beam splitters)
 measured
(homodyne detection)
16
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

17. Gaussian operations
Gaussian states can be
efficiently:
 displaced
(classical currents)
 squeezed
(nonlinear crystals)
 rotated
(phase plates, beam splitters)
 measured
(homodyne detection)
17
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

18. Gaussian operations
Gaussian states can be
efficiently:
 displaced
(classical currents)
 squeezed
(nonlinear crystals)
 rotated
(phase plates, beam splitters)
 measured
(homodyne detection)
18
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

19. Gaussian operations
Gaussian states can be
efficiently:
 displaced
(classical currents)
 squeezed
(nonlinear crystals)
 rotated
(phase plates, beam splitters)
 measured
(homodyne detection)
19
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

20. Gaussian states: formalism
• Up to local unitaries, Gaussian states are completely
specified by the covariance matrix…
• … or equivalently by the
four symplectic invariants
20
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
standard
form
TAB
a c
a d
c b
d b
a g
s s
g b
æ ö÷ç ÷ç ÷çæ ö ÷ç ÷÷ç ç ÷÷ç= = = ç ÷÷ç ç ÷÷ç ÷÷ç çè ø ÷ç ÷ç ÷ç ÷çè ø
det , det , det , detA B C Da b g s= = = =

21. Gaussian POVMs
21
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
• All the measurements that can be done by linear optics
(appending Gaussian ancillas, manipulating with
symplectic transformations, plus homodyne detection):
• The posterior state of A after measuring B has a
covariance matrix (independent of the measurement outcome)
1 0 † †
1 2 0
0
is the density
ˆ
matrix of a
single-mode Gaussian state with covariance ma
ˆ ˆ ˆ ˆ( ) ( ) ( ), where ( ) exp( )
trix
,
( ) , and
B B B B B
B B
W W W b b
d
h p h h h h h
p h h
s
- *
-
P = P = -
P = Pò 1
|A h
ð
e
1
0
( ) T
e a g b s g-
= - +

22. Gaussian quantum discord
• The Gaussian quantum discord is the quantum discord
of a bipartite Gaussian state where the optimization in
the conditional entropy is restricted to Gaussian POVMs
• and can be rewritten as
▫ where the symplectic eigenvalues are
22
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
( |)
( ) ( ) ( ) inf ( ) ( )
B
AB B AB B A
D S S d p S hh
h h¬
P
= - + òð ð ð ð
0
( ) ( ) ( ) ( ) inf ( det )AB
D f B f f f
s
s n n e¬
- +
= - - +
2 2
2 4 , 2D A B Cn±
= D ± D - D = + +

23. Gaussian quantum discord
• Optimal POVM: heterodyne for squeezed thermal states,
homodyne for another class of states, something in-
between for the other two-mode Gaussian states
23
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
( )( ) ( )( )
( )
( ) ( ) ( )
( ) ( )
0
2 2
2 2
2
22 4 2
2 1 2 | | 1
, 1 ;
1inf det( )
2
, .
2
C B A D C C B A D
D AB B C A D
B
AB C D C AB D C AB D
otherwise
B
s
e
ìï + - + - + + + - + - +ïïï - £ + +ïï - +ï= í
ïïï - + - + - + - +ïïïïî

24. Discord/separability/entanglement
• By relating the nullity of discord with saturation of
strong subadditivity of entropy, we demonstrated
that (for finite mean energies) the only two-mode
Gaussian states with zero Gaussian discord
are product states
• All correlated Gaussian states (including all
entangled states and all non-product separable
mixed states) are quantumly correlated!
• This proves the truly quantum nature of Gaussian
states despite their positive Wigner function…
24
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

25. • Consider this class of states (box=two-mode squeezing)
▫ s: initial entanglement; r: entanglement degradation
25
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
Discord/separability/entanglement
s
A
B
C
r
AB
s *
when ,
0
1
s r
¬
®
® ¥
®
®
D
D

26. 26
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
max discord is limited
if 1 en
to
tangled
1
¬
> ÞD
Discord/separability/entanglement

27. 27
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States
Discord/separability/entanglement
( )AB
s® *
D
( )AB
s¬ *
D
: Gaussian Entanglement of FormationG
E
1

28. Other results & comments
• Via the Koashi-Winter duality between entanglement and
one-way classical correlations we can derive a closed formula
for the Gaussian EoF of a family of three-mode Gaussian
states
• Only in very special cases we can prove that the Gaussian
quantum discord realizes the absolute minimum in the
conditional entropy optimization not constrained to Gaussian
POVMs (this is related to the problem of additivity of bosonic
channel capacity etc…)
• It would be interesting to prove, or show counterexamples to
it, that Gaussian POVMs are always optimal among all
continuous variable measurements (including photodetection
etc.)
28
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

29. Summary
• The concept of quantum correlations goes beyond
entanglement
• Quantum discord is a bona fide measure of such general
quantum correlations
• Quantum discord can be computed for Gaussian states
under Gaussian measurements
• All correlated Gaussian states have quantum correlations
• They are limited for separable states
• They admit upper and lower bounds as a function of the
entanglement, for entangled states
29
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

30. Open problems
• Maximum discord for separable states in any
dimension.
▫ known for qubits,
numerically, to be 1/3
Al-Qasimi & James, arXiv:1007.1814
30
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

31. Open problems
• Operational interpretation of discord
• Usefulness of quantum correlations in separable
states for quantum information processing
• Understanding connection with other
nonclassicality indicators in continuous variable
systems (e.g. in terms of P function)
• Producing a theory of quantum correlations, with
axioms to be satisfied by any valid measure of
quantum correlations (e.g. nonincreasing under
local operations and classical communication…)
• …
31
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States

32. Thank you
Imperial College London 10/08/2010Quantum versus Classical Correlations in Gaussian States