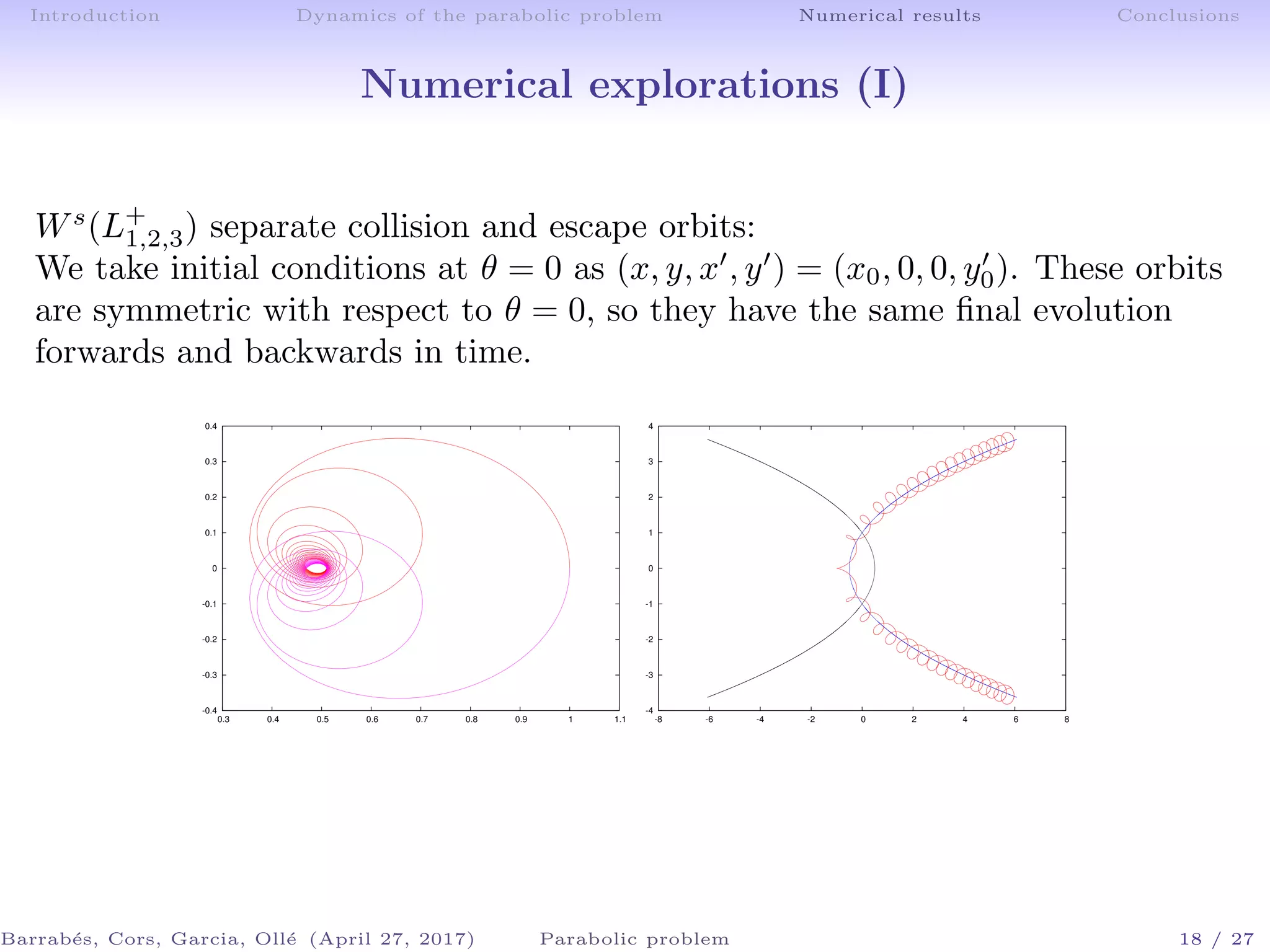
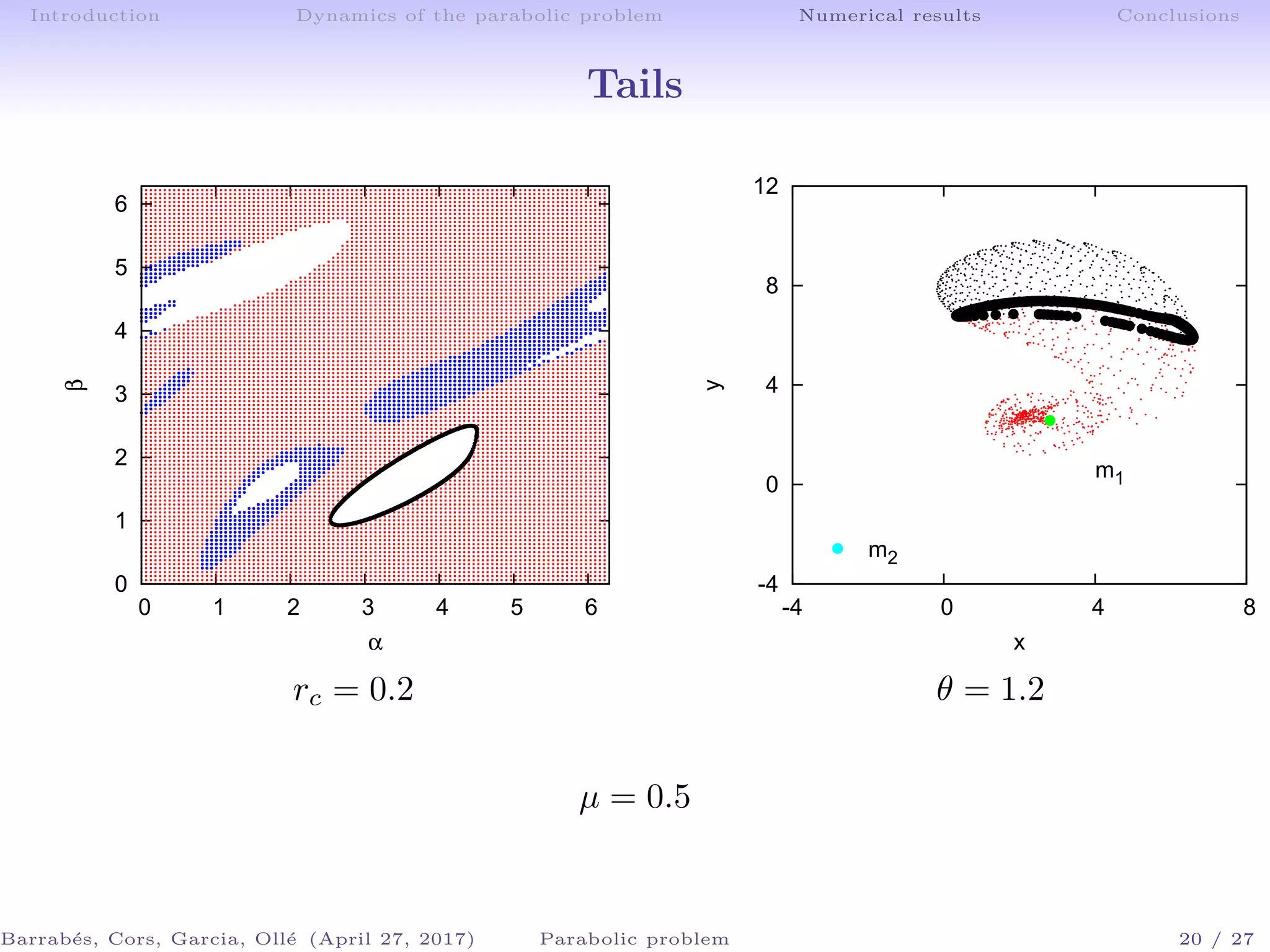
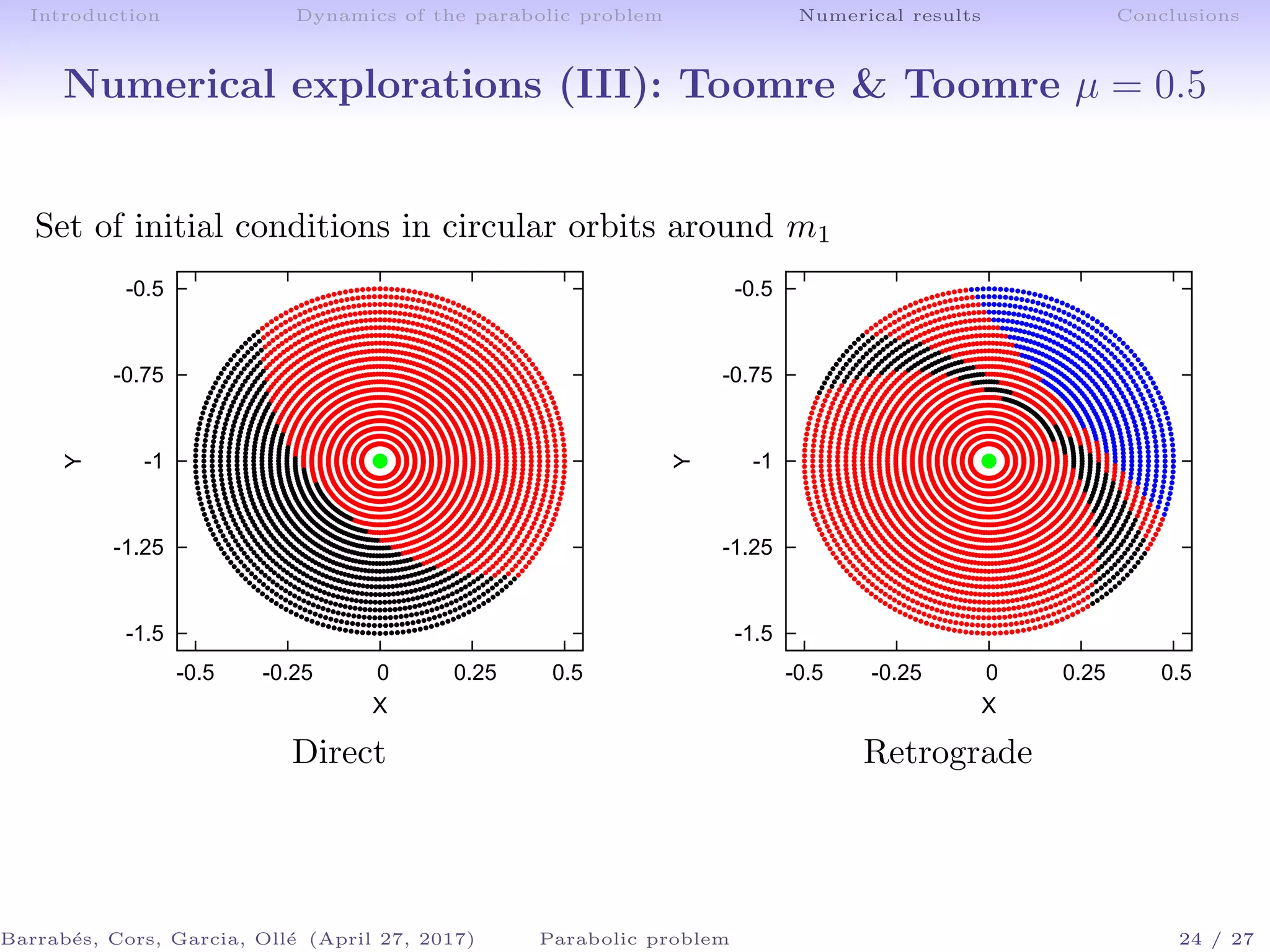
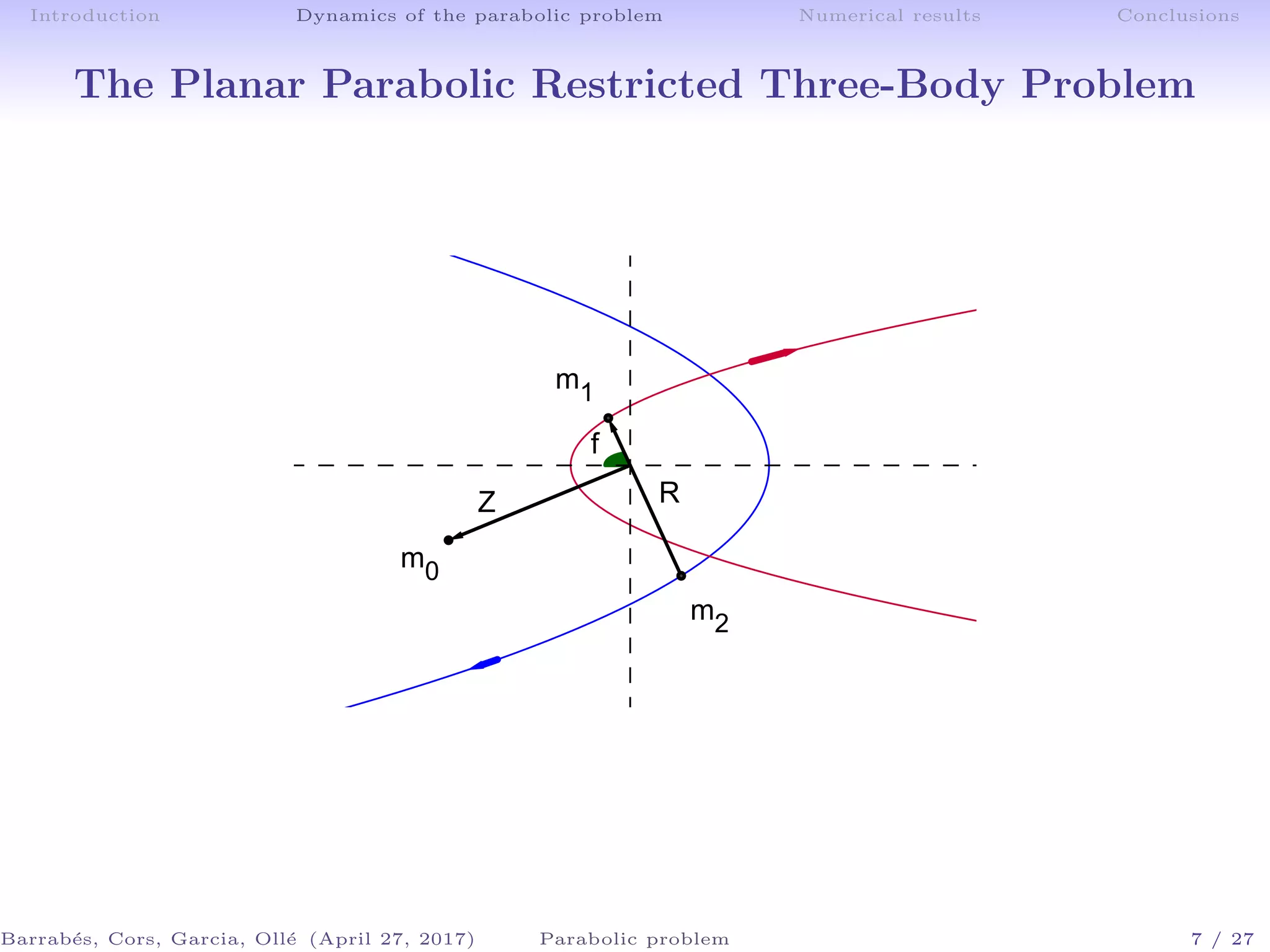
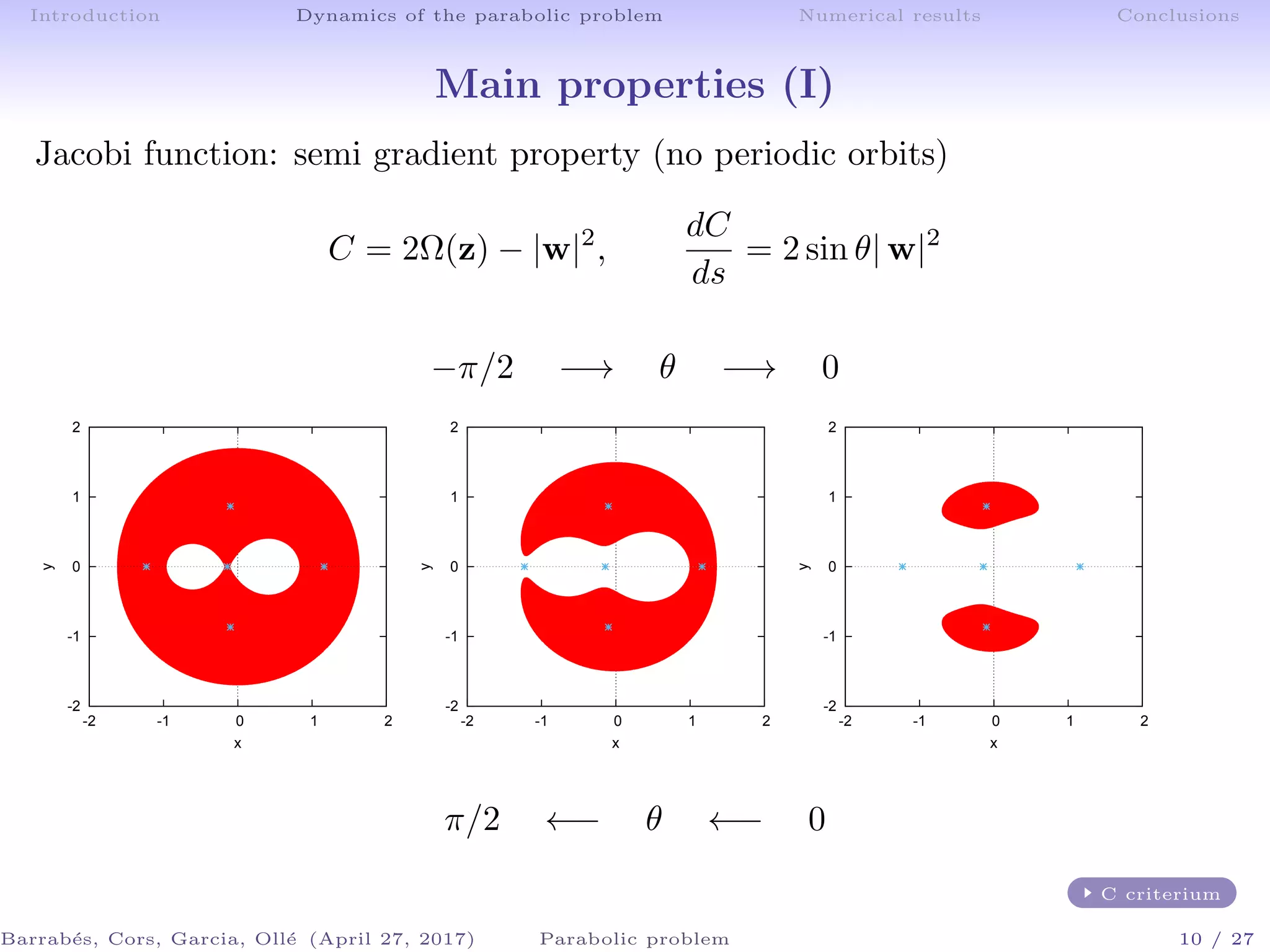
The document discusses the dynamics of galactic encounters using a parabolic restricted three-body problem framework. It examines the conditions that lead to the formation of bridges and tails in galaxies based on numerical simulations and theoretical analyses. Key findings include the identification of equilibrium points and the role of invariant manifolds in determining the outcomes of galactic interactions.

1. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Dynamical generation of galactic bridges and tails
using a parabolic restricted three-body problem
E. Barrab´es 1
J.M. Cors 2
L. Garcia1
M. Oll´e2
1
Universitat de Girona
2
Universitat Polit`ecnica de Catalunya
BMD 2017
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 1 / 27

2. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Outline
Introduction
Dynamics of the parabolic problem
Numerical results
Conclusions
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 2 / 27

3. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Galactic encounters: bridges and tails
Belokurov, Erkal, Deason, Koposov, De Angeli, Evans, Fraternali and Mackkey.
Clouds, streams and bridges: redrawing the blueprint of the Magellanic
System with Gaia DR1.
Monthly Notices of the Royal Astronomical Society, 466: 4711–4730, 2017.
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 3 / 27

4. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Galactic encounters: bridges and tails
Galaxies NGC 3808A (right) and NGC 3808B (left). Credits: NASA, Hubble
Space Telescope (2015)
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 3 / 27

5. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Galactic encounters: bridges and tails
9
Tails!
Arp 173
• NGC 2992/3
http://www.astrooptik.com/Bildergalerie/PolluxGallery/NGC2623.htm www.etsu.edu/physics/bsmith/research/sg/arp.html
http://www.ess.sunysb.edu/fwalter/SMARTS/findingcharts.html
NGC 2623
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 3 / 27

6. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Galactic encounters: bridges and tails (II)
Toomre, A. and Toomre, J. Galactic bridges and tails, The Astrophysical
Journal, 178, 1972.
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 4 / 27

7. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Aim
To study the mechanisms that explain the existence
of bridges considering a very simple model: the planar
parabolic restricted three-body problem.
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 5 / 27

8. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Outline
Introduction
Dynamics of the parabolic problem
Numerical results
Conclusions
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 6 / 27

9. Introduction Dynamics of the parabolic problem Numerical results Conclusions
The Planar Parabolic Restricted Three-Body Problem
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 7 / 27

10. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Equations (I)
Parabolic problem:
d2
Z
dt2
= −(1 − µ)
Z − Z1
|Z − Z1|3
− µ
Z − Z2
|Z − Z2|3
,
Z1 = µR and Z2 = (µ − 1)R, and R = (σ2
− 1, 2σ) is the relative position
vector from m2 to m1 where σ = tan(f/2), and f is the true anomaly
Change to a synodic frame (primaries at fixed positions) + change of time:
z1 = (µ, 0), z2 = (µ − 1, 0),
dt
ds
=
√
2 r3/2
.
Compatification to extend the flow when the primaries are at infinity
(t, s → ±∞):
sin(θ) = tanh(s).
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 8 / 27

11. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Equations (II): Global System



dθ
ds
= cos θ,
dz
ds
= w,
dw
ds
= −A(θ)w + Ω(z)
A(θ) =
sin θ 4 cos θ
−4 cos θ sin θ
,
Ω(z) = x2
+ y2
+ 2
1 − µ
(x − µ)2 + y2
+ 2
µ
(x − µ + 1)2 + y2
.
θ = ±π/2 are invariant → Boundary problems
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 9 / 27

12. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Main properties (I)
Jacobi function: semi gradient property (no periodic orbits)
C = 2Ω(z) − |w|2
,
dC
ds
= 2 sin θ| w|2
−π/2 −→ θ −→ 0
-2
-1
0
1
2
-2 -1 0 1 2
y
x
-2
-1
0
1
2
-2 -1 0 1 2
y
x
-2
-1
0
1
2
-2 -1 0 1 2
y
x
π/2 ←− θ ←− 0
C criterium
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 10 / 27

13. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Main properties (II)
Equilibrium points at ±π
2 :
-2
-1
0
1
2
-2 -1 0 1 2
y
x
Collinear L±
1 , L±
2 , L±
3
Triangular L±
4 , L±
5
L+
1,3 L+
2 L+
4,5
dim(Wu
) 1 2
dim(Ws
) 4 3
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 11 / 27

14. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Main properties (II)
Homothetic solutions and connections
θ = π/2
θ = −π/2
θ = 0
L+
1
L+
4
L+
3
L−
3
L−
4
L−
1
The three bodies keep the same configuration all the time: either the three
bodies lie in a line (collinear configuration) or they lie at the vertices of an
equilateral triangle (triangular configuration)
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 12 / 27

15. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Main properties (II)
Homothetic solutions and connections
θ = π/2
θ = −π/2
θ = 0
L+
1
L+
4
L+
3
L−
3
L−
4
L−
1
The intersection of the invariant manifolds give a map of connections in each
boundary
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 12 / 27

16. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Final evolutions
Proposition (Final evolutions)
Let γ(s) = (θ(s), z(s), w(s)), s ∈ [0, ∞), be a solution of
the global system. Then, either:
it is a collision orbit,
lims→∞ |z(s)| = ∞ (escape orbit)
its ω-limit is an equilibrium point.
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 13 / 27

17. Introduction Dynamics of the parabolic problem Numerical results Conclusions
C-criterium
Proposition
Let q ∈ Int(D) with θ ≥ 0, and γ(s) = (θ(s), z(s), w(s)),
s ∈ [0, ∞), the solution of the global system through q. Then,
(i) if for some time s0 the value of the Jacobi function
C(γ(s0)) > C2 and z(s) is located in one of the bounded
components of the Hill’s region, then it is a collision orbit;
(ii) if for some time s0 the value of the Jacobi function
C(γ(s0)) > C1 and z(s) is located in the unbounded
component of the Hill’s region, then it is an escape orbit.
Hill’s regions
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 14 / 27

18. Introduction Dynamics of the parabolic problem Numerical results Conclusions
The collision manifold
Regularization of the equations of motion using McGehee’s ideas and
variables to remove one singularity r1 = 0 or r2 = 0 (collision):
x − xmi
= r cos δ v = r1/2
r
y = r sin δ u = r1/2
rδ
ds
dτ
= r3/2
In the regularized equations r = 0 is the collision manifold
There exist two cylinders of equilibrium points:
T±
= {(r, δ, v, u, θ) ∈ R5
| r = 0, v = ±v0, u = 0, δ ∈ [0, 2π], θ ∈ [−π/2, π/2]}
with v0 = 2 (1 − µ).
The unstable (stable) invariant manifold associated to T+
(T−
) is 4
dimensional.
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 15 / 27

19. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Outline
Introduction
Dynamics of the parabolic problem
Numerical results
Conclusions
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 16 / 27

20. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Generating bridges and tails
There exist of only three different types of final evolutions (enriched due
to existence of the homothetic solutions)
The invariant manifolds Wu
(L−
1,2,3) and Ws
(L+
1,2,3) are of codimension 1:
they behave as a frontier and divide the phase space in regions where only
one of the other two final evolutions are allowed: escape or collision
These frontiers are the responsible of the existence of bridges and tails
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 17 / 27

21. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Numerical explorations (I)
Ws
(L+
1,2,3) separate collision and escape orbits:
We take initial conditions at θ = 0 as (x, y, x , y ) = (x0, 0, 0, y0). These orbits
are symmetric with respect to θ = 0, so they have the same final evolution
forwards and backwards in time.
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1
-4
-3
-2
-1
0
1
2
3
4
-8 -6 -4 -2 0 2 4 6 8
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 18 / 27

22. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Numerical explorations (I)
Ws
(L+
1,2,3) separate collision and escape orbits:
L−
3 → L+
3
L−
1 → L+
1
L−
2 → L+
2
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 18 / 27

23. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Numerical explorations (I)
Ws
(L+
1,2,3) separate collision and escape orbits:
-4.2
-4.1
-4
-3.9
-3.8
-1.05 -1 -0.95 -0.9
y
’
x
m1
m2
-1.5
-1
-0.5
0
0.5
1
-1.5 -1 -0.5 0 0.5 1
y
x
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 18 / 27

24. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Numerical explorations (II): Bridges and Tails
Fix an initial value of C and θ = −π/4 and take initial conditions as:
x = xmi
+ rc cos α x = v cos β
y = rc sin α y = v sin β
0
1
2
3
4
5
6
0 1 2 3 4 5 6
β
α
0
1
2
3
4
5
6
0 1 2 3 4 5 6
β
α
rc = 0.001 rc = 0.2
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 19 / 27

25. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Tails
0
1
2
3
4
5
6
0 1 2 3 4 5 6
β
α
-4
0
4
8
12
-4 0 4 8
m1
m2
y
x
rc = 0.2 θ = 1.2
µ = 0.5
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 20 / 27

26. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Bridges
0
1
2
3
4
5
6
0 1 2 3 4 5 6
β
α
-4
-2
0
2
4
-4 -2 0 2 4
m1
m2
y
x
rc = 0.2 θ = 1.2
µ = 0.5
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 21 / 27

27. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Bridge and Tail
3
3.25
3.5
3.75
4
5 5.1 5.2 5.3 5.4 5.5
β
α
-8
-4
0
4
8
-8 -4 0 4 8
y
x
m1
m2
µ = 0.5
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 22 / 27

28. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Bridge and Tail
-8
-6
-4
-2
0
2
4
-6 -4 -2 0 2 4
Y
X
m1
m2
-12
-10
-8
-6
-4
-2
0
2
-6 -4 -2 0 2
Y
X
m1
m2
µ = 0.3 µ = 0.1
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 23 / 27

29. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Numerical explorations (III): Toomre & Toomre µ = 0.5
Set of initial conditions in circular orbits around m1
-1.5
-1.25
-1
-0.75
-0.5
-0.5 -0.25 0 0.25 0.5
Y
X
-1.5
-1.25
-1
-0.75
-0.5
-0.5 -0.25 0 0.25 0.5Y
X
Direct Retrograde
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 24 / 27

30. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Numerical explorations (III): Toomre & Toomre µ = 0.3
m1
-1.25
-1
-0.75
-0.5
-0.25
0
-0.5 -0.25 0 0.25 0.5
Y
X
-1.25
-1
-0.75
-0.5
-0.25
0
-0.5 -0.25 0 0.25 0.5
Y
X
m2
1
1.25
1.5
1.75
2
-0.5 -0.25 0 0.25 0.5
Y
X
1
1.25
1.5
1.75
2
-0.5 -0.25 0 0.25 0.5
Y
X
Direct Retrograde
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 25 / 27

31. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Outline
Introduction
Dynamics of the parabolic problem
Numerical results
Conclusions
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 26 / 27

32. Introduction Dynamics of the parabolic problem Numerical results Conclusions
Conclusions
The existence of heteroclinic orbits between the
collinear equilibrium points and the collision manifold
associated to the primaries are the responsible of the
formation of bridges and tails in a parabolic restricted
three body problem
Barrab´es, Cors, Garcia, Oll´e (April 27, 2017) Parabolic problem 27 / 27