Dic rd theory_quantization_07

Rate Distortion Theory & Quantization

Rate Distortion Theory
Rate Distortion Function
R(D*) for Memoryless Gaussian Sources
R(D*) for Gaussian Sources with Memory
Scalar Quantization
Lloyd-Max Quantizer
High Resolution Approximations
Entropy-Constrained Quantization
Vector Quantization

Thomas Wiegand: Digital Image Communication RD Theory and Quantization 1

Rate Distortion Theory
Theoretical discipline treating data compression from
the viewpoint of information theory.
Results of rate distortion theory are obtained without
consideration of a specific coding method.
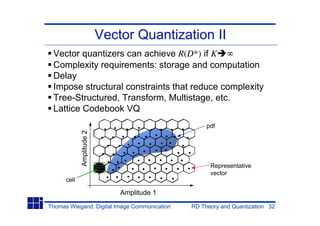
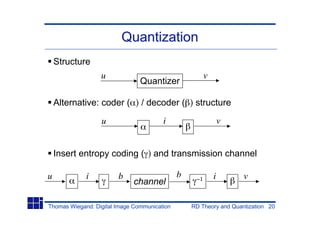
Goal: Rate distortion theory calculates minimum
transmission bit-rate R for a given distortion D and
source.


Transmission System

Distortion D
U V
Source Coder Decoder Sink

Bit-Rate R

Need to define U, V, Coder/Decoder, Distortion D, and
Rate R
Need to establish functional relationship between U,
V, D, and R


Definitions
Source symbols are given by the random sequence {U k }
• Each U k assumes values in the discrete set = {u0 ,u1,...,uM 1 }
- For a binary source: U = {0,1}
- For a picture: U = {0,1,...,255}
• For simplicity, let us assume U k to be independent and
identically distributed (i.i.d.) with distribution {P(u),u U}

Reconstruction symbols are given by the random sequence {Vk }
with distribution {P(v),v }
• Each Vk assumes values in the discrete set = {v 0 ,v1,...,v N 1}
• The sets and need not to be the same


Coder / Decoder
Statistical description of Coder/Decoder, i.e. the mapping of the
source symbols to the reconstruction symbols, via
Q = {Q(v | u),u ,v }

is the conditional probability distribution over the letters of the
reconstruction alphabet given a letter of the source alphabet
Transmission system is described via
Joint pdf: P(u,v)
P(u) = P(u,v)
v

P(v) = P(u,v)
u

P(u,v) = P(u) Q(v | u) (Bayes‘ rule)

Distortion
To determine distortion, we define a non-negative cost function
d(u,v),d(.,.) : [0, )

Examples for d
0, for u v
• Hamming distance: d(u,v) =
1, for u = v

2
• Squared error: d(u,v) = u v

Average Distortion D(Q) = P(u) 244 d(u,v)
14 Q(v |3
4 u)
u v P (u,v )


Mutual Information
Shannon average mutual information
I = H(U) H(U |V )
= P(u) ld P(u) + P(u,v) ld P(u | v)
u u v

P(u,v)
= - P(u,v) ld P(u) + P(u,v) ld
u v u v
P(v)
P(u,v)
= P(u,v) ld
u v
P(u) P(v)

Using Bayes‘ rule
Q(v | u)
I(Q) = 14 244 ld
P(u) Q(v |3
4 u)
u v P(u,v )
P(v)
with P(v) = P(u) Q(v | u)
u


Rate
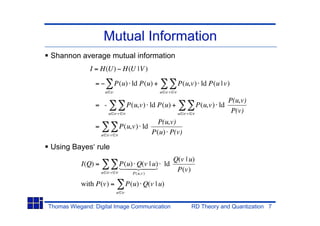
Shannon average mutual information expressed via
entropy
I(U;V ) = H(U) H(U |V )
Source entropy Equivocation: conditional entropy

Equivocation:
• The conditional entropy (uncertainty) about the
source U given the reconstruction V
• A measure for the amount of missing [quantized]
information in the received signal V


Rate Distortion Function
Definition: R(D*) = min {I(Q)}
Q:D(Q) D*

For a given maximum average distortion D, the rate
distortion function R(D*) is the lower bound for the
transmission bit-rate.
The minimization is conducted for all possible
mappings Q that satisfy the average distortion
constraint.
R(D*) is measured in bits for ld .


Discussion
In information theory: maximize mutual information for efficient
communication
In rate distortion theory: minimize mutual information
In rate distortion theory: source is given, not the channel
Problem which is addressed:
Determine the minimum rate at which information about the source
must be conveyed to the user in order to achieve a prescribed
fidelity.
Another view: Given a prescribed distortion, what is the channel
with the minimum capacity to convey the information.
Alternative definition via interchanging the roles of rate and
distortion


Distortion Rate Function

Definition: D(R*) = min {d(Q)}
Q:I(Q) R*

For a given maximum average rate R , the distortion
rate function R(D*) is the lower bound for the average
distortion.

Here, we can set R(D*) to the capacity C of the
transmission channel and determine the minimum
distortion for this ideal communication system


Properties of the Rate Distortion Function, I

R(D) for a discrete amplitude source
(H(U),Dmin = 0)

(H(U) H(U |V ) = 0,Dmax )

0 D
0 Dmax
1

R(D) is well defined for D (Dmin ,Dmax )
For discrete amplitude sources, Dmin = 0
R(D) = 0, if D > Dmax


Properties of the Rate Distortion Function, II
R(D) is always positive
0 I(U;V ) H(U)

R(D) is non-increasing in D
R(D) is strictly convex downward in the range (Dmin ,Dmax )
The slope of R(D) is continous in the range (Dmin ,Dmax )
R(D)

0 D
0 1 Dmax

Shannon Lower Bound
It can be shown that H(U V |V) = H(U |V )

R(D*) = min {H(U) H(U |V )}
Q:D(Q) D*
Then we can write
= H(U) max {H(U |V )}
Q:D(Q) D*

= H(U) max {H(U V |V )}
Q:D(Q) D*

Ideally, the source coder would produce distortions
u v that are statistically independent from the
reconstructed signal v (not always possible!).

Shannon Lower Bound: R(D*) H(U) max H(U V )
Q:D(Q) D*


R(D*) for a Memoryless Gaussian Source
and MSE Distortion
Gaussian source, variance 2
Mean squared error (MSE) D = E{(u v) 2 }
2
1 2 2 R*
R(D*) = log ; D(R*) = 2 ,R 0
2 D*
2
SNR = 10 log10 = 10 log10 2 2 R 6R [dB]
D

Rule of thumb: 6 dB ~ 1 bit
The R(D*) for non-Gaussian sources with the same
variance 2 is always below this Gaussian R(D*) curve.


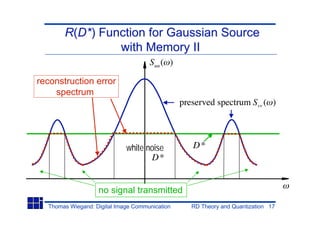
R(D*) Function for Gaussian Source
with Memory I
Jointly Gaussian source with power spectrum Suu ( )
MSE: D = E{(u v) 2 }
Parametric formulation of the R(D*) function

D= 1 min[D*,Suu ( )]d
2
1 Suu ( )
R= 1 max[0, log ]d
2 2 D*

R(D*) for non-Gaussian sources with the same power
spectral density is always lower.


with Memory II
Suu ( )

reconstruction error
spectrum
preserved spectrum Svv ( )

white noise D*
D*

no signal transmitted

with Memory III
ACF and PSD for a first order AR(1) Gauss-Markov
process: U[n] = Z[n] + U[n 1]
2
|k| 2 (1 2 )
Ruu (k) = , Suu ( ) = 2
1 2 cos +
Rate Distortion Function:
1 Suu ( ) D* 1
R(D*) = log 2 d , 2
4 D* 1+
2
1 (1 2 ) 1 2
= log 2 d log 2 (1 2 cos + )d
4 D* 4
2 2
1 (1 2 ) 1
= log 2 = log 2 z
2 D* 2 D*

with Memory IV
SNR [dB] 45
2
40 D* 1 =0,99
= 10 log10
D 2
1+ =0,95
35
=0,9
30 =0,78
25 =0,5
=0
20
15
10
5
0 R [bits]
0 0.5 1 1.5 2 2.5 3 3.5 4

Quantization
Structure
u v
Quantizer

Alternative: coder ( ) / decoder ( ) structure

u i v

Insert entropy coding ( ) and transmission channel

u i b b 1 i v
channel


Scalar Quantization
Average distortion Output v
vi+2
N
D = E{d(U,V )} reconstruction
levels
N 1 uk+1 vi+1
= d(u,v k ) fU (u) du
k= 0 uk vi
ui ui+1 ui+1
Assume MSE
input
d(u,v k ) = (u v k ) 2 signal u
N 1 uk+1
N-1 decision
2
D= (u v k ) fU (u) du thresholds
k= 0 uk

Fixed code word length vs. variable code word length
R = logN vs. R = E{log P(v)}

Lloyd-Max Quantizer
0: Given: a source distribution fU (u)
a set of reconstruction levels {v k }
1: Encode given {v k } (Nearest Neighbor Condition):
(u) = argmin {d(u,v k )} uk = (v k + v k +1 ) 2 (MSE)
2: Update set of reconstruction levels given (Centroid
Condition): u k+1

u fU (u)du
uk
v k = argmin E{d(u,v k ) | (u) = k} vk = uk+1
(MSE)
fU (u)du
uk

3: Repeat steps 1 and 2 until convergence


Pdf of U is roughly constant over individual cells Ck
fU (u) fk, u Ck

The fundamental theorem of calculus
uk+1

Pk = Pr(u Ck ) = fU (u) du (uk +1 uk ) f k = f
k k
uk

Approximate average distortion (MSE)
N 1 uk+1 N 1 uk+1

D= (u v k ) 2 fU (u) du = fk (u v k ) 2 du
k= 0 uk k= 0 uk
N 1
1 N1
3
k 2
= fk = Pk k
k= 0
12 12 k= 0

Uniform Quantization
Reconstruction levels of quantizer { k } , k K are
uniformly spaced
Quantizer step size, i.e. distance v
between reconstruction levels:
Average distortion
N 1
Pk = 1, k =
k= 0
u
N 1 2 N 1 2
1
D= Pk 2k = Pk =
12 k= 0 12 k= 0 12
Closed-form solutions for pdf-optimized uniform
quantizers for Gaussian RV only exist for N=2 and N=3
Optimization of is conducted numerically


Panter and Dite Approximation
Approximate solution for optimized spacing of
reconstruction and decision levels
Assumptions: high resolution and smooth pdf (u)
const
(u) =
3 f (u)
U

Optimal pdf of reconstruction levels is not the same as
for the input levels
1 1
Average Distortion D ( fU 3 (u) du) 3
12N 2
Operational distortion rate function for Gaussian RV
2 3 2 2R
U ~ N(0, ), D(R) 2
2

Entropy-Constrained Quantization
So far: each reconstruction level is transmitted with fixed code
word length
Encode reconstruction levels with variable code word length
Constrained design criteria:
min D, s.t. R < Rc or min R, s.t. D < Dc
Pose as unconstrained optimization via Lagrangian formulation:
min D + R

R Lines of constant For a given , an optimum is obtained
slope: -1/ corresponding to either Rc or Dc
If small, then D small and R large
if large, then D large and R small
Optimality also for functions that are
neither continuous nor differentiable

D


Chou, Lookabaugh, and Gray Algorithm*
0: Given: a source distribution fU (u)
a set of reconstruction levels {vk}
a set of variable length code (VLC) words { k}
with associated length | k|
1: Encode given {vk} and { k}:
(u) = argmin {d(u, vk) + | k| }
2: Update VLC given (uk) and {vk}
| k| = -log P( (u)=k)
3: Update set of reconstruction levels given (uk) and { k}
vk = argmin E { d(u, vk) | (u)=k}
4: Repeat steps 1 - 3 until convergence
*1989, has been proposed for Vector Quantization


Entropy-Constrained Scalar Quantization:
Assume: uniform quantization: Pk=fk
N 1 N 1
R= Pk log Pk = f k log ( f k )
k= 0 k= 0
N 1 N 1
= f k log ( f k ) f k log ( )
du k= 0 k= 0

fU (u) log ( fU (u))du log fU (u) du
1444 2444 3
4 4 14243
Differential Entropy h(U ) 1

= h(U) log
Operational distortion rate function for Gaussian RV
2 e 2 2R
U ~ N(0, ),D(R) 2
6
It can be shown that for high resolution:
Uniform Entropy-Constrained Scalar Quantization is optimum

Comparison for Gaussian Sources
30
SNR [dB] R(D*), =0.9
2 R(D*), =0
= 10 log10 25 Lloyd-Max
D Uniform Fixed-Rate
Panter & Dite App
Entropy-Constrained Opt.
20

15

10

5
R [bits]
0
0 0.5 1 1.5 2 2.5 3 3.5 4

Vector Quantization
So far: scalars have been quantized
Encode vectors, ordered sets of scalars
Gain over scalar quantization (Lookabaugh and Gray 1989)
• Space filling advantage
- Z lattice is not most efficient sphere packing in K-D (K>1)
- Independent from source distribution or statistical dependencies
- Maximum gain for K : 1.53 dB
• Shape advantage
- Exploit shape of source pdf
- Can also be exploited using entropy-constrained scalar
quantization
• Memory advantage
- Exploit statistical dependencies of the source
- Can also be exploited using DPCM, Transform coding, block
entropy coding


Comparison for Gauss-Markov Source: =0.9
40
SNR [dB]
35
30
25
20
15 R(D*), =0.9
VQ, K=100
VQ, K=10
10 VQ, K=5
VQ, K=2
5 Panter & Dite App
Entropy-Constrained Opt.
R [bits]
0
0 1 2 3 4 5 6 7

Vector Quantization II
Vector quantizers can achieve R(D*) if K
Complexity requirements: storage and computation
Delay
Impose structural constraints that reduce complexity
Tree-Structured, Transform, Multistage, etc.
Lattice Codebook VQ

• • pdf
• • • • • •
Amplitude 2

• • • • • • • • •
• • • • • • • •
• •
• • • • • • •
• • • • • • • •
Representative
• • • • • • • • •
vector
cell • • • • • • •

Amplitude 1

Summary
Rate-distortion theory: minimum bit-rate for given distortion
R(D*) for memoryless Gaussian source and MSE: 6 dB/bit
R(D*) for Gaussian source with memory and MSE: encode
spectral components independently, introduce white noise,
suppress small spectral components
Lloyd-Max quantizer: minimum MSE distortion for given number of
representative levels
Variable length coding: additional gains by entropy-constrained
quantization
Minimum mean squared error for given entropy: uniform quantizer
(for fine quantization!)
Vector quantizers can achieve R(D*) if K - Are we done ?
No! Complexity of vector quantizers is the issue

Design a coding system with optimum rate distortion performance,
such that the delay, complexity, and storage requirements are met.


Dic rd theory_quantization_07

More Related Content

What's hot

Viewers also liked

Similar to Dic rd theory_quantization_07

More from wtyru1989

Recently uploaded

Dic rd theory_quantization_07