1. The document discusses discretizing Hamiltonians for Markov chain Monte Carlo (MCMC) methods. Specifically, it examines reproducing Hamiltonian equations through discretization, such as via generalized leapfrog. 2. However, the invariance and stability properties of the continuous-time process may not carry over to the discretized version. Approximations can be corrected with a Metropolis-Hastings step, so exactly reproducing the continuous behavior is not necessarily useful. 3. Discretization induces a calibration problem of determining the appropriate step size. Convergence issues for the MCMC algorithm should not be impacted by imperfect renderings of the continuous-time process in discrete time.

1. About discretising Hamiltonians
Christian P. Robert
Universit´ Paris-Dauphine and CREST
e
http://xianblog.wordpress.com
Royal Statistical Society, October 13, 2010
Christian P. Robert About discretising Hamiltonians

2. Hamiltonian dynamics
Dynamic on the level sets of
1 1
H (θ, p) = −L(θ) + log{(2π)D |G(θ)|} + pT G(θ)−1 p ,
2 2
where p is an auxiliary vector of dimension D, is associated with
Hamilton’s pde’s
∂H ˙ ∂H (θ, p)
˙
p= (θ, p) , θ=
∂p ∂θ
which preserve the potential H (θ, p) and hence the target
distribution at all times t
Christian P. Robert About discretising Hamiltonians

3. Discretised Hamiltonian
Girolami and Calderhead reproduce Hamiltonian equations within
the simulation domain by discretisation via the generalised leapfrog
(!) generator,
[Subliminal French bashing?!]
Christian P. Robert About discretising Hamiltonians

4. Discretised Hamiltonian
Girolami and Calderhead reproduce Hamiltonian equations within
the simulation domain by discretisation via the generalised leapfrog
(!) generator,
but...
Christian P. Robert About discretising Hamiltonians

5. Discretised Hamiltonian
Girolami and Calderhead reproduce Hamiltonian equations within
the simulation domain by discretisation via the generalised leapfrog
(!) generator,
but...
invariance and stability properties of the [background] continuous
time process the method do not carry to the discretised version of
the process [e.g., Langevin]
Christian P. Robert About discretising Hamiltonians

6. Discretised Hamiltonian (2)
Is it useful to so painstakingly reproduce the continuous
behaviour?
Approximations (see R&R’s Langevin) can be corrected by a
Metropolis-Hastings step, so why bother with a second level
of approximation?
Discretisation induces a calibration problem: how long is long
enough?
Convergence issues (for the MCMC algorithm) should not be
impacted by inexact renderings of the continuous time process
in discrete time: loss of efficiency?
Christian P. Robert About discretising Hamiltonians

7. An illustration
Comparison of the fits of discretised Langevin diffusion sequences
to the target f (x) ∝ exp(−x4 ) when using a discretisation step
σ 2 = .1 and σ 2 = .0001, after the same number T = 107 of steps.
0.6
0.5
0.4
Density
0.3
0.2
0.1
0.0
−1.5 −1.0 −0.5 0.0 0.5 1.0 1.5
Christian P. Robert About discretising Hamiltonians

8. An illustration
Comparison of the fits of discretised Langevin diffusion sequences
to the target f (x) ∝ exp(−x4 ) when using a discretisation step
σ 2 = .1 and σ 2 = .0001, after the same number T = 107 of steps.
0.8
0.6
Density
0.4
0.2
0.0
−1.5 −1.0 −0.5 0.0 0.5 1.0 1.5
Christian P. Robert About discretising Hamiltonians

9. An illustration
Comparison of the fits of discretised Langevin diffusion sequences
to the target f (x) ∝ exp(−x4 ) when using a discretisation step
σ 2 = .1 and σ 2 = .0001, after the same number T = 107 of steps.
1e+05
8e+04
6e+04
time
4e+04
2e+04
0e+00
−2 −1 0 1 2
Christian P. Robert About discretising Hamiltonians

10. Back on Langevin
For the Langevin diffusion, the corresponding Langevin
(discretised) algorithm could as well use another scale η for the
gradient, rather than the one τ used for the noise
Christian P. Robert About discretising Hamiltonians

11. Back on Langevin
For the Langevin diffusion, the corresponding Langevin
(discretised) algorithm could as well use another scale η for the
gradient, rather than the one τ used for the noise
y = xt + η∇π(x) + τ ǫt
rather than a strict Euler discretisation
y = xt + τ 2 ∇π(x)/2 + τ ǫt
Christian P. Robert About discretising Hamiltonians

12. Back on Langevin
For the Langevin diffusion, the corresponding Langevin
(discretised) algorithm could as well use another scale η for the
gradient, rather than the one τ used for the noise
y = xt + η∇π(x) + τ ǫt
rather than a strict Euler discretisation
y = xt + τ 2 ∇π(x)/2 + τ ǫt
A few experiments run in Robert and Casella (1999, Chap. 6, §6.5)
hinted that using a scale η = τ 2 /2 could actually lead to
improvements
Christian P. Robert About discretising Hamiltonians

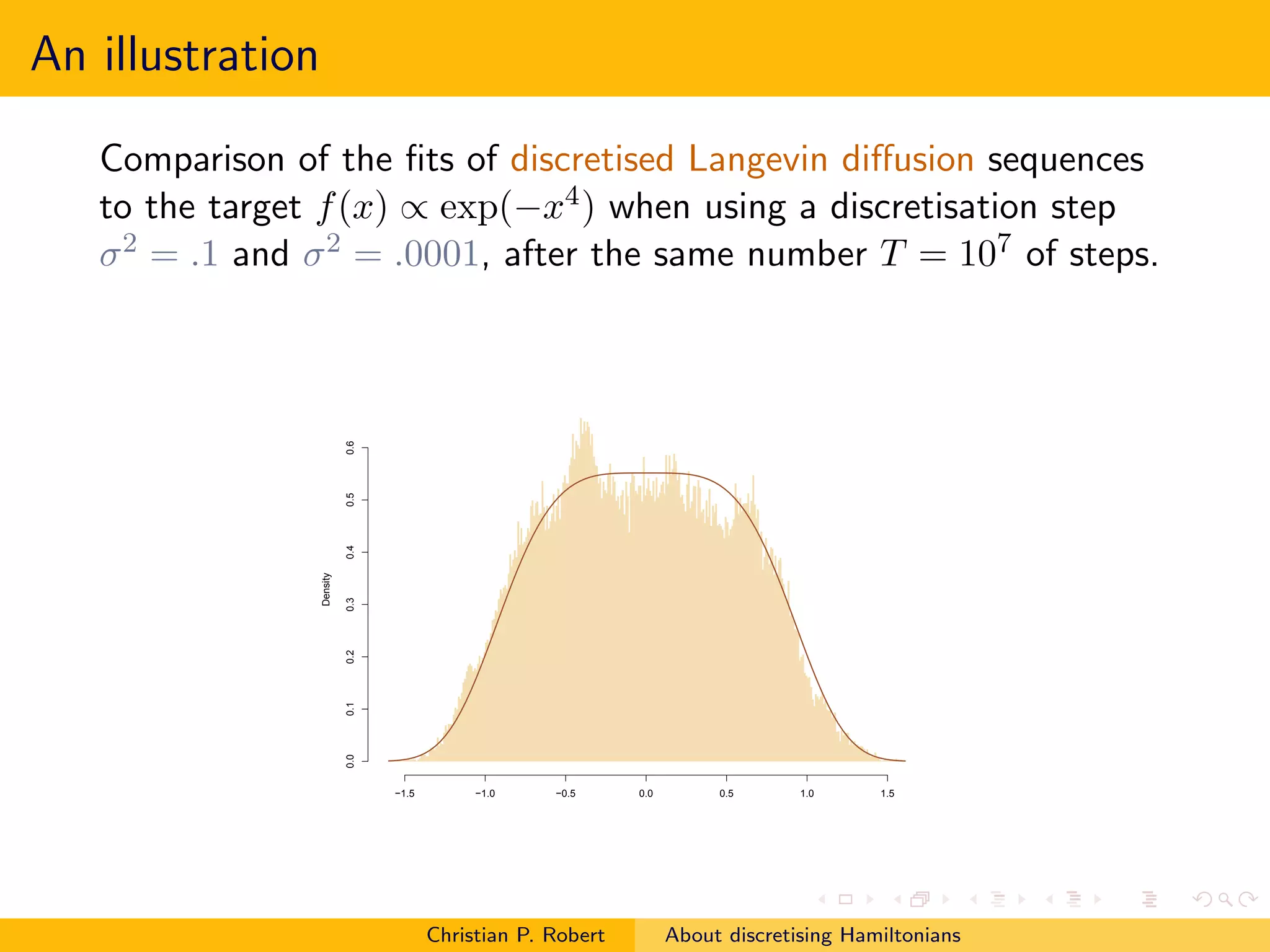
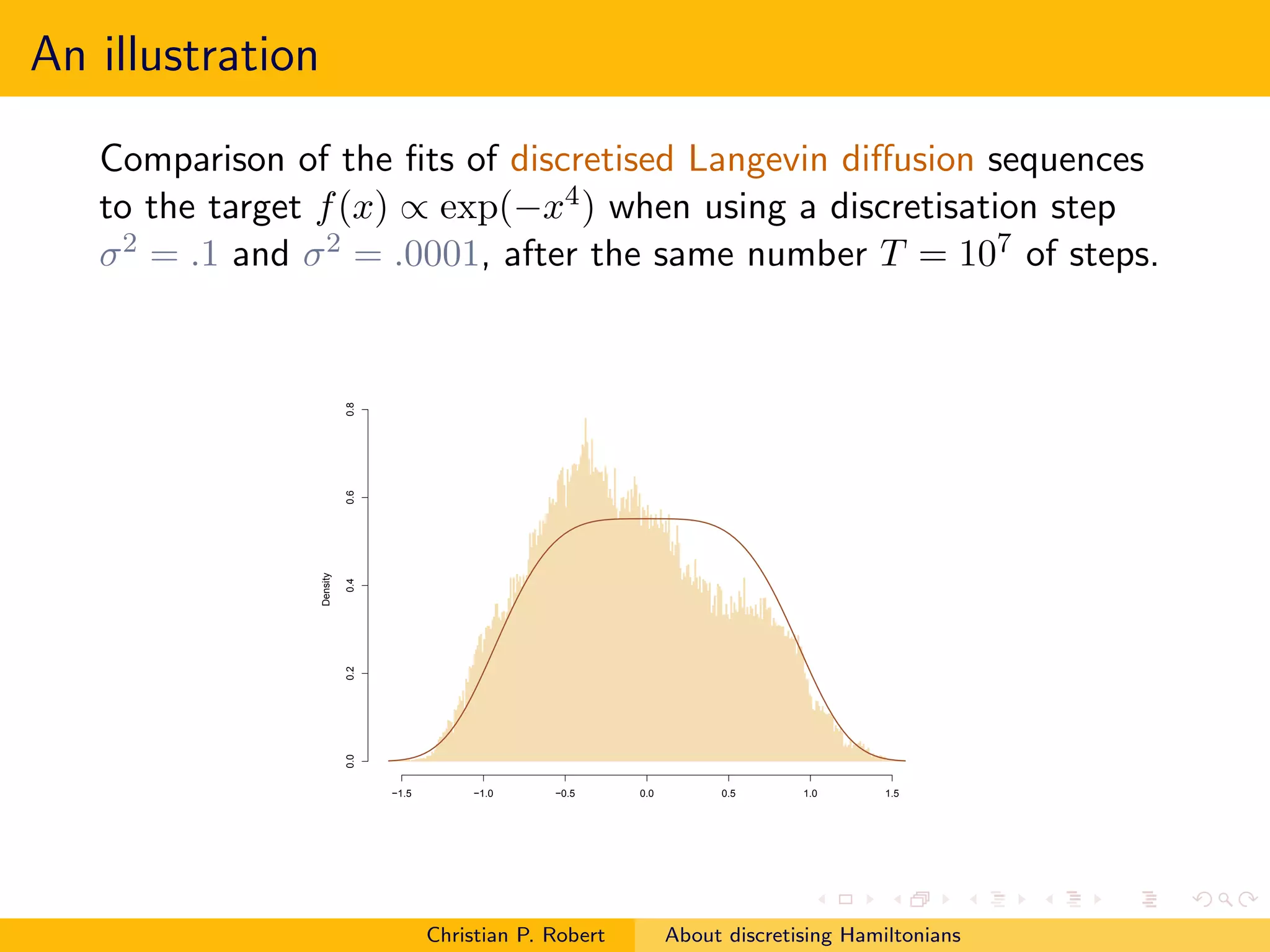
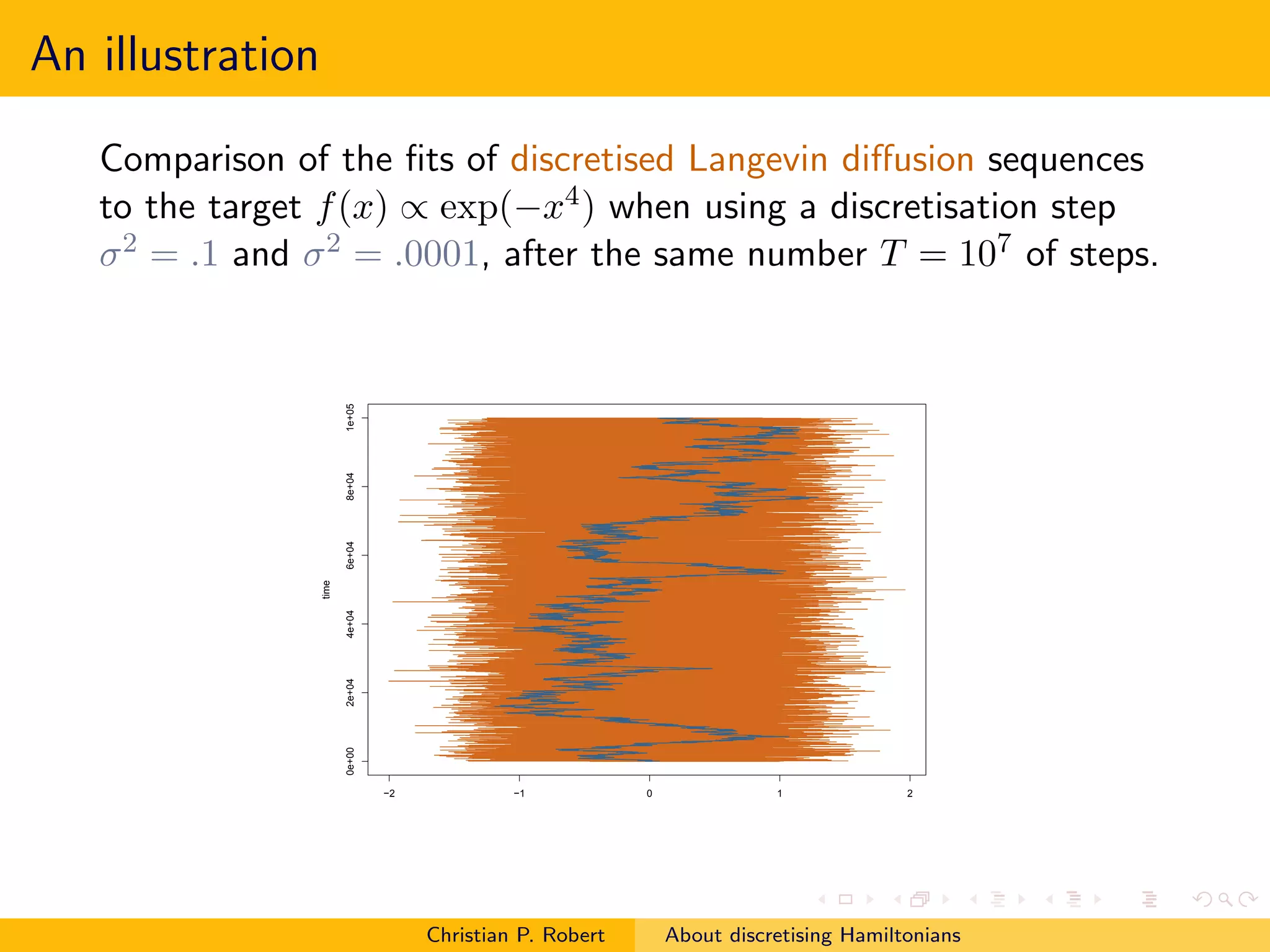
13. Back on Langevin
For the Langevin diffusion, the corresponding Langevin
(discretised) algorithm could as well use another scale η for the
gradient, rather than the one τ used for the noise
y = xt + η∇π(x) + τ ǫt
rather than a strict Euler discretisation
y = xt + τ 2 ∇π(x)/2 + τ ǫt
A few experiments run in Robert and Casella (1999, Chap. 6, §6.5)
hinted that using a scale η = τ 2 /2 could actually lead to
improvements
Which [independent] framework should we adopt for
assessing discretised diffusions?
Christian P. Robert About discretising Hamiltonians