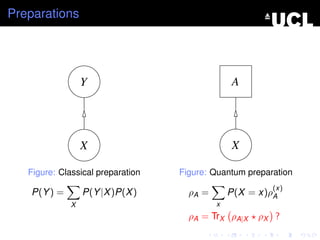
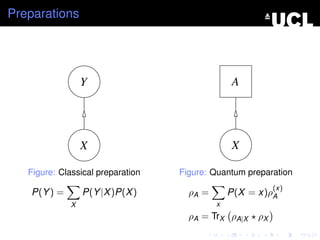
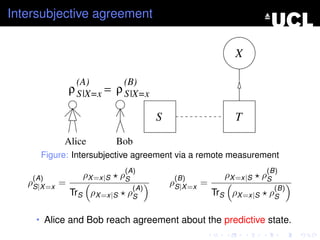
This document discusses quantum conditional states, hybrid quantum-classical systems, and quantum Bayes' rule. It begins by defining quantum conditional states and showing how they relate to reduced and joint quantum states. It then introduces hybrid systems composed of both quantum and classical parts. Quantum conditional states for hybrid systems are defined as sets of quantum states. The document also shows that classical-quantum conditional states correspond to POVMs. Finally, it presents quantum versions of Bayes' rule relating conditional and joint quantum states.

1. Quantum conditional states, Bayes’ rule, and
state compatibility
M. S. Leifer (UCL)
Joint work with R. W. Spekkens (Perimeter)
Imperial College QI Seminar
14th December 2010

2. Outline
1 Quantum conditional states
2 Hybrid quantum-classical systems
3 Quantum Bayes’ rule
4 Quantum state compatibility
5 Further results and open questions

3. Topic
1 Quantum conditional states
2 Hybrid quantum-classical systems
3 Quantum Bayes’ rule
4 Quantum state compatibility
5 Further results and open questions

4. Classical vs. quantum Probability
Table: Basic definitions
Classical Probability Quantum Theory
Sample space Hilbert space
ΩX = {1, 2, . . . , dX } HA = CdA
= span (|1 , |2 , . . . , |dA )
Probability distribution Quantum state
P(X = x) ≥ 0 ρA ∈ L+ (HA )
x∈ΩX P(X = x) = 1 TrA (ρA ) = 1

5. Classical vs. quantum Probability
Table: Composite systems
Classical Probability Quantum Theory
Cartesian product Tensor product
ΩXY = ΩX × ΩY HAB = HA ⊗ HB
Joint distribution Bipartite state
P(X , Y ) ρAB
Marginal distribution Reduced state
P(Y ) = x∈ΩX P(X = x, Y ) ρB = TrA (ρAB )
Conditional distribution Conditional state
P(Y |X ) = P(X ,Y )
P(X ) ρB|A =?

6. Definition of QCS
Definition
A quantum conditional state of B given A is a positive operator
ρB|A on HAB = HA ⊗ HB that satisfies
TrB ρB|A = IA .
c.f. P(Y |X ) is a positive function on ΩXY = ΩX × ΩY that
satisfies
P(Y = y |X ) = 1.
y ∈ΩY

7. Relation to reduced and joint States
√ √
(ρA , ρB|A ) → ρAB = ρA ⊗ IB ρB|A ρA ⊗ IB
ρAB → ρA = TrB (ρAB )
ρB|A = ρ−1 ⊗ IB ρAB
A ρ−1 ⊗ IB
A

8. Relation to reduced and joint States
√ √
(ρA , ρB|A ) → ρAB = ρA ⊗ IB ρB|A ρA ⊗ IB
ρAB → ρA = TrB (ρAB )
ρB|A = ρ−1 ⊗ IB ρAB
A ρ−1 ⊗ IB
A
Note: ρB|A defined from ρAB is a QCS on supp(ρA ) ⊗ HB .

9. Relation to reduced and joint States
√ √
(ρA , ρB|A ) → ρAB = ρA ⊗ IB ρB|A ρA ⊗ IB
ρAB → ρA = TrB (ρAB )
ρB|A = ρ−1 ⊗ IB ρAB
A ρ−1 ⊗ IB
A
Note: ρB|A defined from ρAB is a QCS on supp(ρA ) ⊗ HB .
P(X ,Y )
c.f. P(X , Y ) = P(Y |X )P(X ) and P(Y |X ) = P(X )

10. Notation
• Drop implied identity operators, e.g.
• IA ⊗ MBC NAB ⊗ IC → MBC NAB
• MA ⊗ IB = NAB → MA = NAB
• Define non-associative “product”
√ √
• M N= NM N

11. Relation to reduced and joint States
√ √
(ρA , ρB|A ) → ρAB = ρA ⊗ IB ρB|A ρA ⊗ IB
ρAB → ρA = TrB (ρAB )
ρB|A = ρ−1 ⊗ IB ρAB
A ρ−1 ⊗ IB
A
Note: ρB|A defined from ρAB is a QCS on supp(ρA ) ⊗ HB .
P(X ,Y )
c.f. P(X , Y ) = P(Y |X )P(X ) and P(Y |X ) = P(X )

12. Relation to reduced and joint states
(ρA , ρB|A ) → ρAB = ρB|A ρA
ρAB → ρA = TrB (ρAB )
ρB|A = ρAB ρ−1
A
Note: ρB|A defined from ρAB is a QCS on supp(ρA ) ⊗ HB .
P(X ,Y )
c.f. P(X , Y ) = P(Y |X )P(X ) and P(Y |X ) = P(X )

13. Classical conditional probabilities
Example (classical conditional probabilities)
Given a classical variable X , define a Hilbert space HX with a
preferred basis {|1 X , |2 X , . . . , |dX X } labeled by elements of
ΩX . Then,
ρX = P(X = x) |x x|X
x∈ΩX
Similarly,
ρXY = P(X = x, Y = y ) |xy xy |XY
x∈ΩX ,y ∈ΩY
ρY |X = P(Y = y |X = x) |xy xy |XY
x∈ΩX ,y ∈ΩY

14. Topic
1 Quantum conditional states
2 Hybrid quantum-classical systems
3 Quantum Bayes’ rule
4 Quantum state compatibility
5 Further results and open questions

15. Correlations between subsystems
X Y A B
Figure: Classical correlations Figure: Quantum correlations
ρAB = ρB|A ρA
P(X , Y ) = P(Y |X )P(X )

16. Preparations
Y A
X X
Figure: Classical preparation Figure: Quantum preparation
(x)
P(Y ) = P(Y |X )P(X ) ρA = P(X = x)ρA
X x
ρA = TrX ρA|X ρX ?

17. What is a Hybrid System?
• Composite of a quantum system and a classical random
variable.
• Classical r.v. X has Hilbert space HX with preferred basis
{|1 X , |2 X , . . . , |dX X }.
• Quantum system A has Hilbert space HA .
• Hybrid system has Hilbert space HXA = HX ⊗ HA

18. What is a Hybrid System?
• Composite of a quantum system and a classical random
variable.
• Classical r.v. X has Hilbert space HX with preferred basis
{|1 X , |2 X , . . . , |dX X }.
• Quantum system A has Hilbert space HA .
• Hybrid system has Hilbert space HXA = HX ⊗ HA
• Operators on HXA restricted to be of the form
MXA = |x x|X ⊗ MX =x,A
x∈ΩX

19. Quantum|Classical QCS are Sets of States
• A QCS of A given X is of the form
ρA|X = |x x|X ⊗ ρA|X =x
x∈ΩX
Proposition
ρA|X is a QCS of A given X iff each ρA|X =x is a normalized state
on HA
(x)
• Ensemble decomposition: ρA = x P(X = x)ρA

20. Quantum|Classical QCS are Sets of States
• A QCS of A given X is of the form
ρA|X = |x x|X ⊗ ρA|X =x
x∈ΩX
Proposition
ρA|X is a QCS of A given X iff each ρA|X =x is a normalized state
on HA
• Ensemble decomposition: ρA = x P(X = x)ρA|X =x

21. Quantum|Classical QCS are Sets of States
• A QCS of A given X is of the form
ρA|X = |x x|X ⊗ ρA|X =x
x∈ΩX
Proposition
ρA|X is a QCS of A given X iff each ρA|X =x is a normalized state
on HA
• Ensemble decomposition: ρA = TrX ρX ρA|X

22. Quantum|Classical QCS are Sets of States
• A QCS of A given X is of the form
ρA|X = |x x|X ⊗ ρA|X =x
x∈ΩX
Proposition
ρA|X is a QCS of A given X iff each ρA|X =x is a normalized state
on HA
√ √
• Ensemble decomposition: ρA = TrX ρX ρA|X ρX

23. Quantum|Classical QCS are Sets of States
• A QCS of A given X is of the form
ρA|X = |x x|X ⊗ ρA|X =x
x∈ΩX
Proposition
ρA|X is a QCS of A given X iff each ρA|X =x is a normalized state
on HA
• Ensemble decomposition: ρA = TrX ρA|X ρX

24. Quantum|Classical QCS are Sets of States
• A QCS of A given X is of the form
ρA|X = |x x|X ⊗ ρA|X =x
x∈ΩX
Proposition
ρA|X is a QCS of A given X iff each ρA|X =x is a normalized state
on HA
• Ensemble decomposition: ρA = TrX ρA|X ρX
• Hybrid joint state: ρXA = x∈ΩX P(X = x) |x x|X ⊗ ρA|X =x

25. Preparations
Y A
X X
Figure: Classical preparation Figure: Quantum preparation
(x)
P(Y ) = P(Y |X )P(X ) ρA = P(X = x)ρA
X x
ρA = TrX ρA|X ρX

26. Measurements
Y Y
X A
Figure: Noisy measurement Figure: POVM measurement
(y )
P(Y ) = P(Y |X )P(X ) P(Y = y ) = TrA EA ρA
X
ρY = TrA ρY |A ρA ?

27. Classical|Quantum QCS are POVMs
• A QCS of Y given A is of the form
ρY |A = |y y |Y ⊗ ρY =y |A
y ∈ΩY
Proposition
ρY |A is a QCS of Y given A iff ρY =y |A is a POVM on HA
(y )
• Generalized Born rule: P(Y = y ) = TrA EA ρA

28. Classical|Quantum QCS are POVMs
• A QCS of Y given A is of the form
ρY |A = |y y |Y ⊗ ρY =y |A
y ∈ΩY
Proposition
ρY |A is a QCS of Y given A iff ρY =y |A is a POVM on HA
• Generalized Born rule: P(Y = y ) = TrA ρY =y |A ρA

29. Classical|Quantum QCS are POVMs
• A QCS of Y given A is of the form
ρY |A = |y y |Y ⊗ ρY =y |A
y ∈ΩY
Proposition
ρY |A is a QCS of Y given A iff ρY =y |A is a POVM on HA
• Generalized Born rule: ρY = TrA ρY |A ρA

30. Classical|Quantum QCS are POVMs
• A QCS of Y given A is of the form
ρY |A = |y y |Y ⊗ ρY =y |A
y ∈ΩY
Proposition
ρY |A is a QCS of Y given A iff ρY =y |A is a POVM on HA
√ √
• Generalized Born rule: ρY = TrA ρA ρY |A ρA

31. Classical|Quantum QCS are POVMs
• A QCS of Y given A is of the form
ρY |A = |y y |Y ⊗ ρY =y |A
y ∈ΩY
Proposition
ρY |A is a QCS of Y given A iff ρY =y |A is a POVM on HA
• Generalized Born rule: ρY = TrA ρY |A ρA

32. Classical|Quantum QCS are POVMs
• A QCS of Y given A is of the form
ρY |A = |y y |Y ⊗ ρY =y |A
y ∈ΩY
Proposition
ρY |A is a QCS of Y given A iff ρY =y |A is a POVM on HA
• Generalized Born rule: ρY = TrA ρY |A ρA
√ √
• Hybrid joint state: ρYA = y ∈ΩY |y y |Y ⊗ ρA ρY =y |A ρA

33. Topic
1 Quantum conditional states
2 Hybrid quantum-classical systems
3 Quantum Bayes’ rule
4 Quantum state compatibility
5 Further results and open questions

34. Classical Bayes’ rule
• Two expressions for joint probabilities:
P(X , Y ) = P(Y |X )P(X )
= P(X |Y )P(Y )
• Bayes’ rule:
P(X |Y )P(Y )
P(Y |X ) =
P(X )
• Laplacian form of Bayes’ rule:
P(X |Y )P(Y )
P(Y |X ) =
Y P(X |Y )P(Y )

35. Quantum Bayes’ rule
• Two expressions for bipartite states:
ρAB = ρB|A ρA
= ρA|B ρB
• Bayes’ rule:
ρB|A = ρA|B ρ−1 ⊗ ρB
A
• Laplacian form of Bayes’ rule
−1
ρB|A = ρA|B TrB ρA|B ρB ⊗ ρB

36. State/POVM duality
• A hybrid joint state can be written two ways:
ρXA = ρA|X ρX = ρX |A ρA
• The two representations are connected via Bayes’ rule:
−1
ρX |A = ρA|X ρX ⊗ TrX ρA|X ρX
−1
ρA|X = ρX |A TrA ρX |A ρA ⊗ ρA
√ √
P(X = x)ρA|X =x ρA ρX =x|A ρA
ρX =x|A = ρA|X =x =
x ∈ΩX P(X = x )ρA|X =x TrA ρX =x|A ρA

37. State update rules
• Classically, upon learning X = x:
P(Y ) → P(Y |X = x)
• Quantumly: ρA → ρA|X =x ?

38. State update rules
• Classically, upon learning X = x:
P(Y ) → P(Y |X = x)
• Quantumly: ρA → ρA|X =x ?
• When you don’t know the value of X
A state of A is:
ρA = TrX ρA|X ρX
= P(X = x)ρA|X =x
X x∈ΩX
Figure: Preparation • On learning X=x: ρA → ρA|X =x

39. State update rules
• Classically, upon learning Y = y :
P(X ) → P(X |Y = y )
• Quantumly: ρA → ρA|Y =y ?
Y • When you don’t know the value of Y
state of A is:
ρA = TrY ρY |A ρA
A
• On learning Y=y: ρA → ρA|Y =y ?
Figure: Measurement

40. Projection postulate vs. Bayes’ rule
• Generalized Lüders-von Neumann projection postulate:
√ √
ρY =y |A ρA ρY =y |A
ρA →
TrA ρY =y |A ρA
• Quantum Bayes’ rule:
√ √
ρA ρY =y |A ρA
ρA →
TrA ρY =y |A ρA

41. Aside: Quantum conditional independence
• General tripartite state on HABC = HA ⊗ HB ⊗ HC :
ρABC = ρC|AB ρB|A ρA

42. Aside: Quantum conditional independence
• General tripartite state on HABC = HA ⊗ HB ⊗ HC :
ρABC = ρC|AB ρB|A ρA
Definition
If ρC|AB = ρC|B then C is conditionally independent of A given B.

43. Aside: Quantum conditional independence
• General tripartite state on HABC = HA ⊗ HB ⊗ HC :
ρABC = ρC|AB ρB|A ρA
Definition
If ρC|AB = ρC|B then C is conditionally independent of A given B.
Theorem
ρC|AB = ρC|B iff ρA|BC = ρA|B

44. Aside: Quantum conditional independence
• General tripartite state on HABC = HA ⊗ HB ⊗ HC :
ρABC = ρC|AB ρB|A ρA
Definition
If ρC|AB = ρC|B then C is conditionally independent of A given B.
Theorem
ρC|AB = ρC|B iff ρA|BC = ρA|B
Corollary
ρABC = ρC|B ρB|A ρA iff ρABC = ρA|B ρB|C ρC

45. Predictive formalism
ρ Y|A Y • Tripartite CI state:
ρXAY = ρY |A ρA|X ρX
• Joint probabilities:
direction
ρ A|X A of ρXY = TrA (ρXAY )
inference
• Marginal for Y :
ρY = TrA ρY |A ρA
ρX X • Conditional probabilities:
Figure: Prep. & meas.
ρY |X = TrA ρY |A ρA|X
experiment

46. Retrodictive formalism
• Due to symmetry of CI:
ρ Y|A Y
ρXAY = ρX |A ρA|Y ρY
• Marginal for X :
ρX = TrA ρX |A ρA
direction
ρ A|X A of • Conditional probabilities:
inference
ρX |Y = TrA ρX |A ρA|Y
• Bayesian update:
ρX X ρA → ρA|Y =y
Figure: Prep. & meas.
• c.f. Barnett, Pegg & Jeffers, J.
experiment
Mod. Opt. 47:1779 (2000).

47. Remote state updates
X ρX|A Y ρY|B
A B
ρ
AB
Figure: Bipartite experiment
• Joint probability: ρXY = TrAB ρX |A ⊗ ρY |B ρAB
• B can be factored out: ρXY = TrA ρY |A ρA|X ρX
• where ρY |A = TrB ρY |B ρB|A

48. Summary of state update rules
Table: Which states update via Bayesian conditioning?
Updating on: Predictive state Retrodictive state
Preparation X
variable
Direct
measurement X
outcome
Remote
measurement It’s complicated
outcome

49. Topic
1 Quantum conditional states
2 Hybrid quantum-classical systems
3 Quantum Bayes’ rule
4 Quantum state compatibility
5 Further results and open questions

50. Introduction to State Compatibility
(A) (B)
ρS ρS
S
Alice Bob
Figure: Quantum state compatibility
• Alice and Bob assign different states to S
• e.g. BB84: Alice prepares one of |0 S , |1 S , |+ S , |− S
I
• Bob assigns dS before measuring
S
(A) (B)
• When do ρS , ρS represent validly differing views?

51. Brun-Finklestein-Mermin Compatibility
• Brun, Finklestein & Mermin, Phys. Rev. A 65:032315
(2002).
Definition (BFM Compatibility)
(A) (B)
Two states ρS and ρS are BFM compatible if ∃ ensemble
decompositions of the form
(A) (A)
ρS = pτS + (1 − p)σS
(B) (B)
ρS = qτS + (1 − q)σS

52. Brun-Finklestein-Mermin Compatibility
• Brun, Finklestein & Mermin, Phys. Rev. A 65:032315
(2002).
Definition (BFM Compatibility)
(A) (B)
Two states ρS and ρS are BFM compatible if ∃ ensemble
decompositions of the form
(A)
ρS = pτS + junk
(B)
ρS = qτS + junk

53. Brun-Finklestein-Mermin Compatibility
• Brun, Finklestein & Mermin, Phys. Rev. A 65:032315
(2002).
Definition (BFM Compatibility)
(A) (B)
Two states ρS and ρS are BFM compatible if ∃ ensemble
decompositions of the form
(A)
ρS = pτS + junk
(B)
ρS = qτS + junk
• Special case:
• If both assign pure states then they must agree.

54. Objective vs. Subjective Approaches
• Objective: States represent knowledge or information.
• If Alice and Bob disagree it is because they have access to
different data.
• BFM & Jacobs (QIP 1:73 (2002)) provide objective
justifications of BFM.

55. Objective vs. Subjective Approaches
• Objective: States represent knowledge or information.
• If Alice and Bob disagree it is because they have access to
different data.
• BFM & Jacobs (QIP 1:73 (2002)) provide objective
justifications of BFM.
• Subjective: States represent degrees of belief.
• There can be no unilateral requirement for states to be
compatible.
• Caves, Fuchs & Shack Phys. Rev. A 66:062111 (2002).

56. Objective vs. Subjective Approaches
• Objective: States represent knowledge or information.
• If Alice and Bob disagree it is because they have access to
different data.
• BFM & Jacobs (QIP 1:73 (2002)) provide objective
justifications of BFM.
• Subjective: States represent degrees of belief.
• There can be no unilateral requirement for states to be
compatible.
• Caves, Fuchs & Shack Phys. Rev. A 66:062111 (2002).
• However, we are still interested in whether Alice and Bob
can reach intersubjective agreement.

57. Subjective Bayesian Compatibility
(A) (B)
ρS ρS
S
Alice Bob
Figure: Quantum compatibility

58. Intersubjective agreement
X
(A) (B)
ρS = ρS
S T
Alice Bob
Figure: Intersubjective agreement via a remote measurement
• Alice and Bob agree on the model for X
(A) (B)
ρX |S = ρX |S = ρX |S , ρX |S = TrT ρX |T ρT |S

59. Intersubjective agreement
X
(A) (B)
ρ S |X=x = ρ S |X=x
S T
Alice Bob
Figure: Intersubjective agreement via a remote measurement
(A) (B)
(A) ρX =x|S ρS (B) ρX =x|S ρS
ρS|X =x = ρS|X =x =
(A) (B)
TrS ρX =x|S ρS TrS ρX =x|S ρS
• Alice and Bob reach agreement about the predictive state.

60. Intersubjective agreement
(A) (B) S
ρ S |X=x = ρ S |X=x
Alice Bob X
Figure: Intersubjective agreement via a preparation vairable
• Alice and Bob reach agreement about the predictive state.

61. Intersubjective agreement
(A) (B) X
ρ S |X=x = ρ S |X=x
Alice Bob S
Figure: Intersubjective agreement via a measurement
• Alice and Bob reach agreement about the retrodictive
state.

62. Subjective Bayesian compatibility
Definition (Quantum compatibility)
(A) (B)
Two states ρS , ρS are compatible iff ∃ a hybrid conditional
state ρX |S for a r.v. X such that
(A) (B)
ρS|X =x = ρS|X =x
for some value x of X , where
(A) (A) (B) (B)
ρXS = ρX |S ρS ρX |S = ρX |S ρS

63. Subjective Bayesian compatibility
Definition (Quantum compatibility)
(A) (B)
Two states ρS , ρS are compatible iff ∃ a hybrid conditional
state ρX |S for a r.v. X such that
(A) (B)
ρS|X =x = ρS|X =x
for some value x of X , where
(A) (A) (B) (B)
ρXS = ρX |S ρS ρX |S = ρX |S ρS
Theorem
(A) (B)
ρS and ρS are compatible iff they satisfy the BFM condition.

64. Subjective Bayesian justification of BFM
BFM ⇒ subjective compatibility.
• Common state can always be chosen to be pure |ψ S
(A) (B)
ρS = p |ψ ψ|S + junk, ρS = q |ψ ψ|S + junk
• Choose X to be a bit with
ρX |S = |0 0|X ⊗ |ψ ψ|S + |1 1|X ⊗ IS − |ψ ψ|S .
• Compute
(A) (B)
ρS|X =0 = ρS|X =0 = |ψ ψ|S

65. Subjective Bayesian justification of BFM
Subjective compatibility ⇒ BFM.
(A) (A) (A) (A)
• ρSX = ρX |S ρS = ρS|X ρX
(A) (A)
ρS = TrX ρSX
(A) (A)
= PA (X = x)ρS|X =x + P(X = x )ρS|X =x
x =x
(A)
= PA (X = x)ρS|X =x + junk
(B) (B)
• Similarly ρS = PB (X = x)ρS|X =x + junk
(A) (B) (A) (B)
• Hence ρS|X =x = ρS|X =x ⇒ ρS and ρS are BFM
compatible.

66. Topic
1 Quantum conditional states
2 Hybrid quantum-classical systems
3 Quantum Bayes’ rule
4 Quantum state compatibility
5 Further results and open questions

67. Further results
Forthcoming paper(s) with R. W. Spekkens also include:
• Dynamics (CPT maps, instruments)
• Temporal joint states
• Quantum conditional independence
• Quantum sufficient statistics
• Quantum state pooling
Earlier papers with related ideas:
• M. Asorey et. al., Open.Syst.Info.Dyn. 12:319–329 (2006).
• M. S. Leifer, Phys. Rev. A 74:042310 (2006).
• M. S. Leifer, AIP Conference Proceedings 889:172–186
(2007).
• M. S. Leifer & D. Poulin, Ann. Phys. 323:1899 (2008).

68. Open question
What is the meaning of fully quantum Bayesian
conditioning?
−1
ρB → ρB|A = ρA|B TrB ρA|B ρB ⊗ ρB

69. Thanks for your attention!
People who gave me money
• Foundational Questions Institute (FQXi) Grant
RFP1-06-006
People who gave me office space when I didn’t have any
money
• Perimeter Institute
• University College London