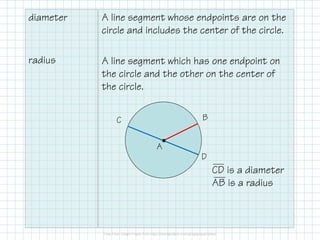
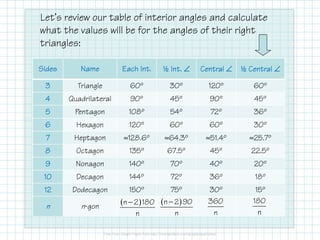
The student is able to develop and use formulas to find the areas of circles and regular polygons. Key formulas include using π to find the circumference and area of a circle based on diameter or radius. For regular polygons, the student can find the area using the apothem and perimeter, or use special formulas for equilateral triangles (s2/3/4) and regular hexagons (6s2/3/4).

1. Obj. 45 Circles & Polygons
The student is able to (I can):
• Develop and use formulas to find the areas of circles and
regular polygons
• Develop and use formulas to find arc length and sector
area of circles

2. circle
The set of all points in a plane that are a
fixed distance from a point, called the
center.
A circle is named by the symbol
center.
•
A
A
and its

3. diameter
A line segment whose endpoints are on the
circle and includes the center of the circle.
radius
A line segment which has one endpoint on
the circle and the other on the center of
the circle.
B
C
•
A
D
CD is a diameter
AB is a radius

4. π (pi)
The ratio of the circumference to the
diameter.
C
π=
d
which becomes C = πd
Since the diameter is twice the radius, this
formula can also be written as:
C = 2πr
π is an irrational number — it never repeats
and it never ends. The symbol π is an exact
number; 3.1415926… is an approximation.

5. If you cut a circle into wedges, and arrange the wedges
into a parallelogram-shaped figure:
A = bh
1
A = circumference i radius
2
1
A = ( 2πradius ) i radius
22
A = πr
radius
1
2
circumference

6. Examples
1. Find the exact circumference and area
of a circle whose diameter is 18.
C = πd = π(18) = 18π
A = πr2 = π(92) = 81π
2. Find the diameter and area of a circle
whose circumference is 22π.
22π = πd
d = 22
A = π(112) = 121π
3. Find the radius of a circle whose area
is 81π.
81π = πr2
81 = r2
r=9

7. central angle
of a circle
An angle whose vertex is on the center of
the circle, and whose sides intersect the
circle.
sector of a
circle
A region bounded by a central angle.
R
A•
G
∠RAG is a central angle
RAG is a sector

8. The area of a sector is proportional to the
area of the circle containing the sector.
Area of sector central angle
=
Area of circle
360°
S
m°
=
2
πr
360°
Formula:
 m° 
S = πr 

 360° 
2

9. Examples
Find the area of each sector. Leave
answers in terms of π.
120°
S = π (2 )
360°
 4 i120 
= π

360 

4
= π in.2
3
2  72° 
S = π ( 10 ) 

360° 

 7200 
= π

 360 
2
1.
120º 2"
•
2.
• 72º
10m
= 20 π m2

10. chord
A line segment whose endpoints are on the
circle.
arc
A portion of a circle.
K
KY is a chord.
E•
Y
KY is an arc.

11. arc measure
The measure of the central angle that
intercepts the arc.
arc length
The distance along an arc. It is
proportional to the circumference of the
circle.
arc length
central angle
=
circumference
360°
mº
•
mº
 m° 
L = C

360° 

where C is the
circumference (either
C=πd or C=2πr).

12. Example
Find each exact arc length.
1.
120º
• 3′
2.
8m
• 72º
120 
L = 2π ( 3 ) 


 360 
= 2 π ft.
72 
L = 2π ( 8 ) 


 360 
=
16
π or 3.2 π m
5

13. apothem
The distance from the center of a polygon
to one of the sides.
central angle
An angle whose vertex is at the center and
whose sides go through consecutive
vertices.
•
central angle

14. For regular polygons, likewise, we can cut out a regular
polygon and arrange the halves as shown:
A = bh
1
A = perimeter i apothem
2
1
A = aP
2
apothem
1
2
perimeter

15. Since all of the central angles have to add
up to 360˚, the measure of a central angle
is
360
n
central angle
apothem

16. If we look at the isosceles triangle created
by a central angle (the apothem is the
height), one of the triangle’s base angle is
½ the interior angle.
central angle
interior angle
apothem
½ interior angle

17. What this means is that on any regular
polygon, we can set up a right triangle, with
one leg as the apothem and one leg as half
the length of a side.
½ central angle
apothem
½ interior angle
½ side
When you are calculating areas, you will
almost always be using the tangent ratio
(opposite/adjacent).

18. Let’s review our table of interior angles and calculate
what the values will be for the angles of their right
triangles:
Sides
Name
Each Int.
½ Int. ∠
Central ∠
½ Central ∠
3
Triangle
60º
30º
120º
60º
4
Quadrilateral
90º
45º
90º
45º
5
Pentagon
108º
54º
72º
36º
6
Hexagon
120º
60º
60º
30º
7
Heptagon
≈128.6º
≈64.3º
≈51.4º
≈25.7º
8
Octagon
135º
67.5º
45º
22.5º
9
Nonagon
140º
70º
40º
20º
10
Decagon
144º
72º
36º
18º
12
Dodecagon
150º
75º
n
n-gon
30º
360
n
15º
180
n
(n − 2 ) 180 (n − 2 ) 90
n
n

19. Examples
1. Find the area of the regular pentagon:
10
Let’s sketch in our
right triangle:
•
36º
a
54°
5
To find the apothem (a), we can use the
tangent ratio:
5
a
tan 36° =
tan54° =
or
5
a
Thus, a ≈ 6.88. The perimeter = 50, so
1
A = (6.88)(50) = 172
2

20. Examples
2. Find the area of the equilateral triangle:
12
60º
•
2 3
6
This is a 30-60-90 triangle, so the
apothem is going to be 6 3 = 2 3
3
Since it is equilateral, the perimeter will be
3(12) = 36. So the area is
1
1
A = aP = 2 3 ( 36 ) = 36 3
2
2
(
)

21. Because the central angle of an equilateral
triangle forms a special right triangle, we
also have a special formula for the area of
an equilateral triangle:
s2 3
(Where s is the
A=
side length.)
4
Looking at the previous example, if we plug
in 12 for s, we get:
122 3 144 3
A=
=
= 36 3
4
4
The advantage of this is that we don’t have
to try to draw in that tiny 30-60-90
triangle. Remember this as “s-2-3-4”.

22. Likewise, because the hexagon is composed
of 6 equilateral triangles, we have a special
formula for the area of a hexagon:
 s2 3 
A = 6

4 

Example: What is the area of a hexagon
with a side length of 14?
 14 2 3 
 196 3 
A = 6
 = 6

4 
4 


(
)
= 6 49 3 = 294 3

23. Summary
• Circle formulas
— C = πd or C = 2πr
— A = πr2
• Regular polygon formulas
1
— A = aP
2
s2 3
— Equilateral triangle: A =
4
 s2 3 
— Regular hexagon: A = 6 
4 

