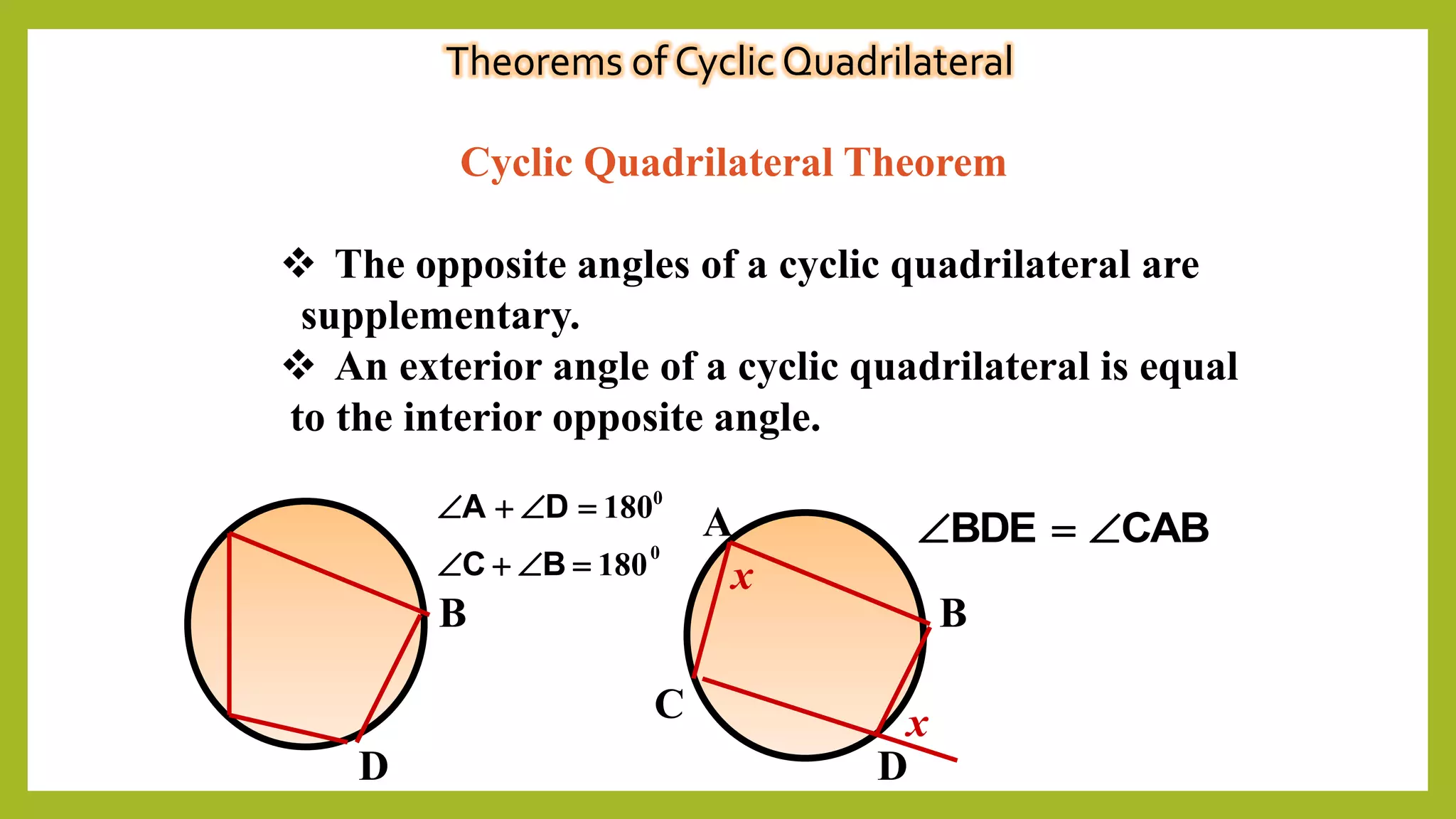
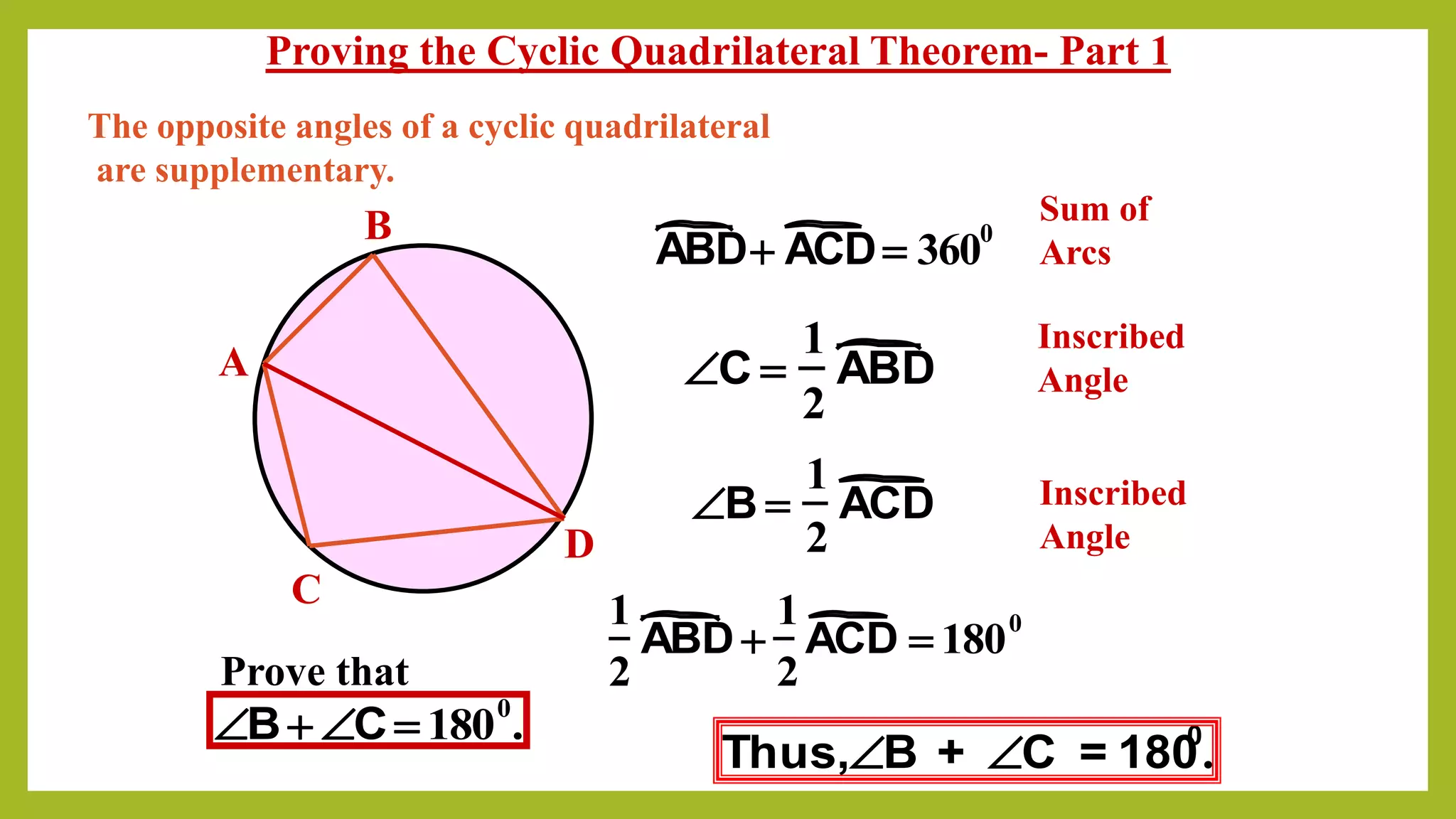
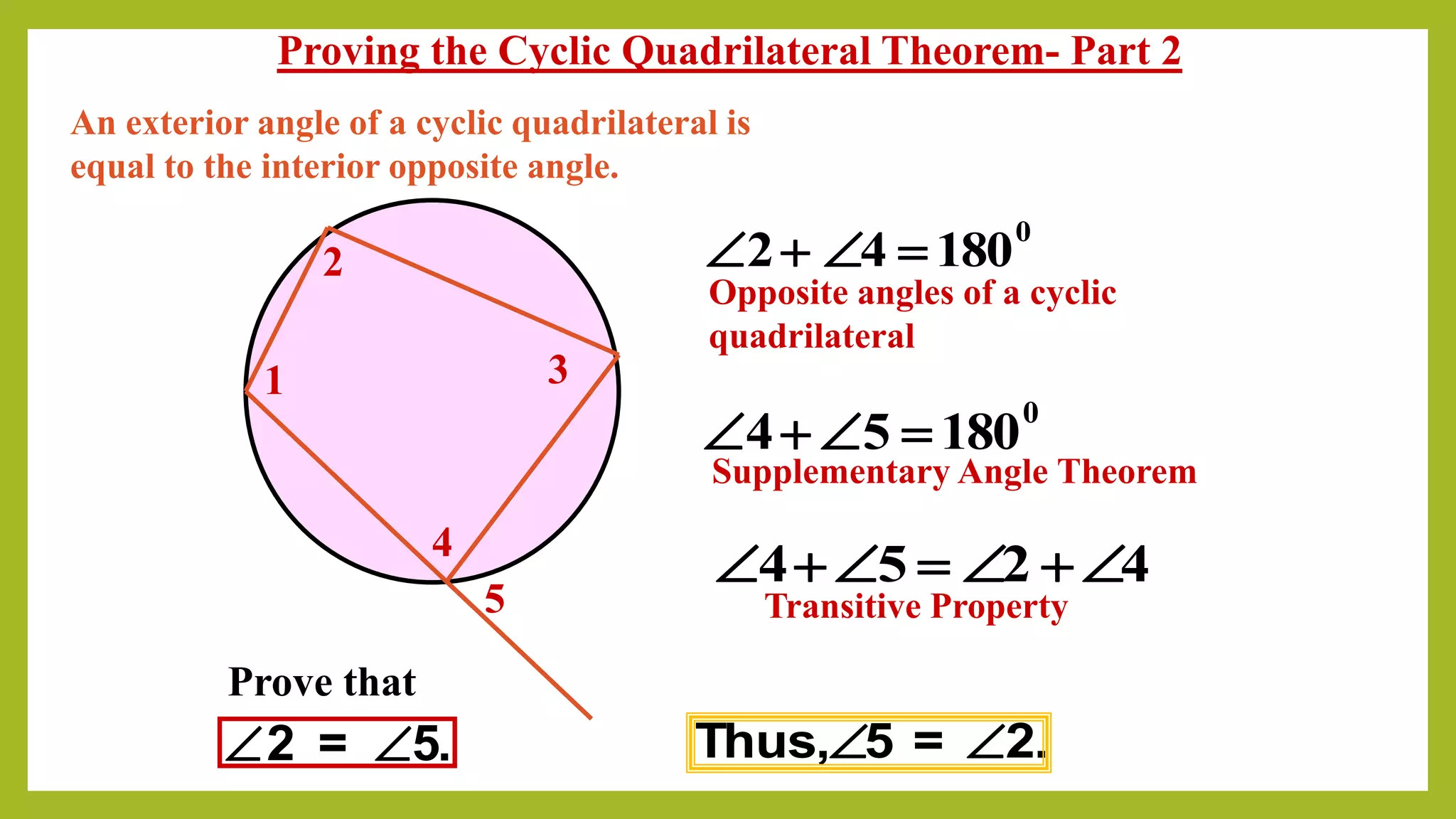
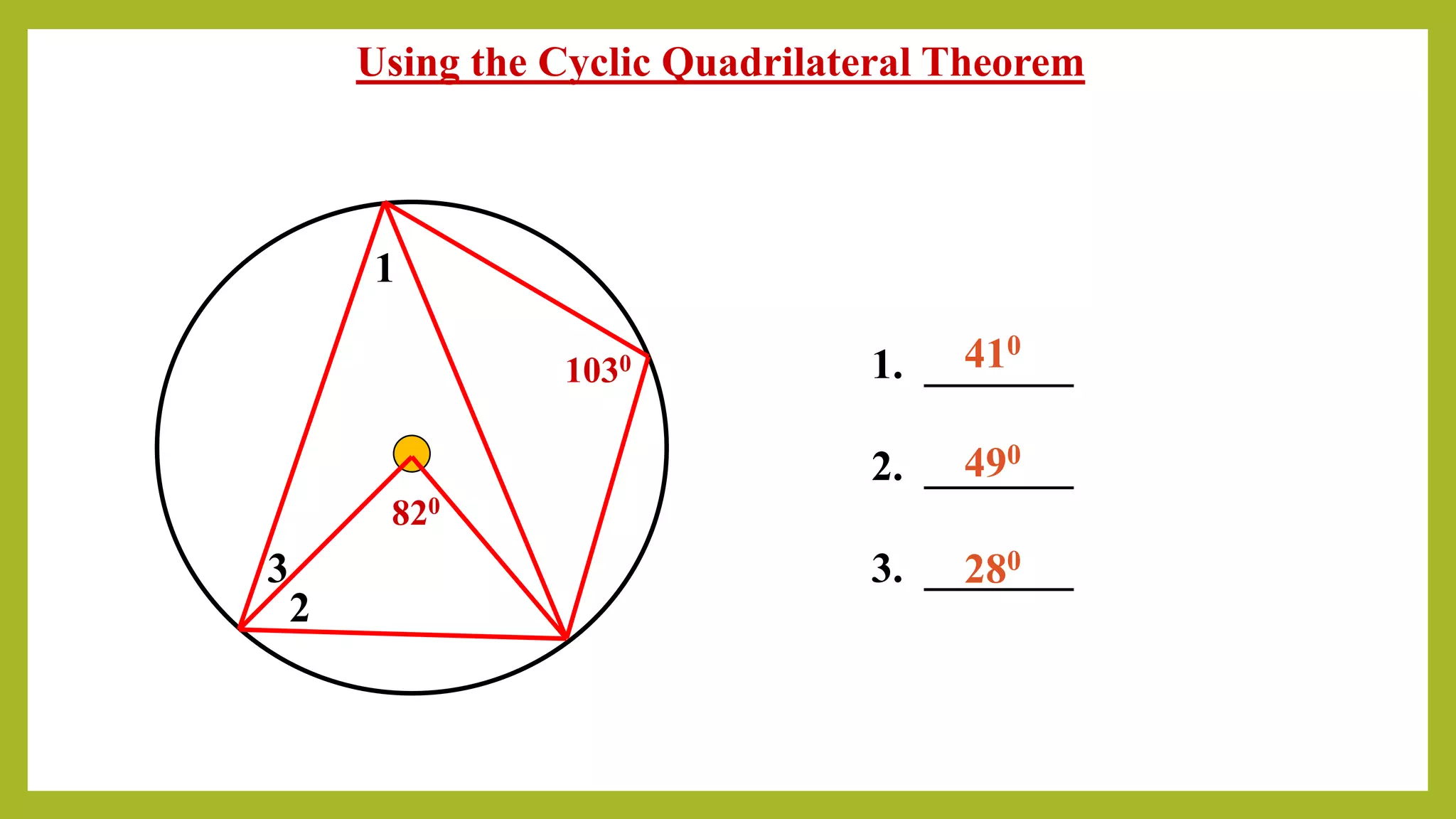
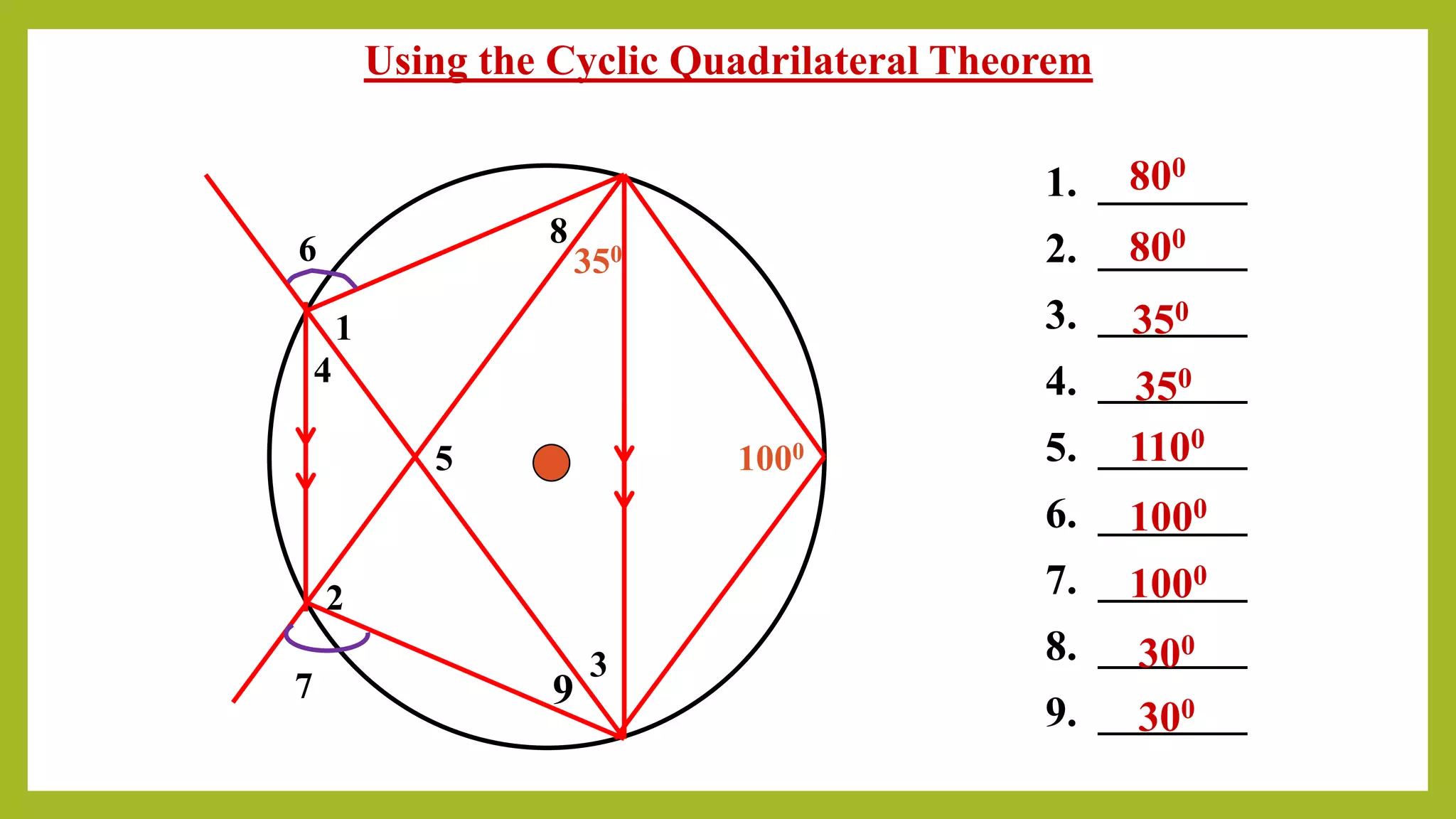
This document is a presentation on cyclic quadrilaterals. It defines a cyclic quadrilateral as a quadrilateral whose vertices all lie on a single circle. It provides key properties of cyclic quadrilaterals, including that opposite angles are supplementary and exterior angles equal interior opposite angles. Formulas are given for the area of a cyclic quadrilateral using Brahmagupta's formula and the circumradius using Parameshvara's formula. Examples are worked through to demonstrate using the cyclic quadrilateral theorems. The conclusion thanks the teacher for the educational assignment.

2. From:
Hitesh Kumar
Durga Prasad
IX ‘B’
J.S.S public school,
Bage
To:
Prabhakhar Sir
Mathematics Department
JSS Public School
Bage

3. Introduction To Cyclic Quadrilaterals
In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is
a quadrilateral whose vertices all lie on a single circle. This circle is called
thecircumcircle or circumscribed circle, and the vertices are said to be
concyclic. The center of the circle and its radius are called the circumcenter
and the circumradius respectively. Other names for these quadrilaterals are
concyclic quadrilateral and chordal quadrilateral, the latter since the sides
of the quadrilateral are chords of the circumcircle. Usually the quadrilateral
is assumed to be convex, but there are also crossed cyclic quadrilaterals.
The formulas and properties given below are valid in the convex case.
The word cyclic is from the Greek kuklos which means "circle" or "wheel".
All triangles have a circumcircle, but not all quadrilaterals do. An example of a quadrilateral
that cannot be cyclic is a non-square rhombus.

4. Properties of a Cyclic Quadrilateral
1. The opposite angles of a cyclic
quadrilateral are supplementary.
or
The sum of either pair of opposite
angles of a cyclic quadrilateral is 1800
2. If one side of a cyclic quadrilateral
are produced, then the exterior angle
will be equal to the opposite interior
angle.
3. If the sum of any pair of opposite
angles of a quadrilateral is 1800, then
the quadrilateral is cyclic.

5. Area of a Cyclic Quadrilateral
The area K of a cyclic quadrilateral with sides a, b, c, d is given by Brahmagupta's formula.
Where s, the semi perimeter, is
. It is a corollary to Bretschneider's formula since
opposite angles are supplementary. If also d = 0, the cyclic quadrilateral becomes a triangle
and the formula is reduced to Heron's formula.
The cyclic quadrilateral has maximal area among all quadrilaterals having the same sequence
of side lengths. This is another corollary to Bretschneider's formula. It can also be proved using
calculus.
Four unequal lengths, each less than the sum of the other three, are the sides of each of three
non-congruent cyclic quadrilaterals, which by Brahmagupta's formula all have the same area.
Specifically, for sides a, b, c, and d, side a could be opposite any of side b, side c, or side d.

6. Parameshvara's Formula
A cyclic quadrilateral with successive sides a, b, c, d and semi perimeter s has the
circumradius (the radius of the circumcircle) given by
R=frac{1}{4} sqrt{frac{(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}.
This was derived by the Indian mathematician Vatasseri Parameshvara in the 15th century.
Using Brahmagupta's formula, Parameshvara's formula can be restated as
4KR=sqrt{(ab+cd)(ac+bd)(ad+bc)}

7. Theorems of Cyclic Quadrilateral
Cyclic Quadrilateral Theorem
 The opposite angles of a cyclic quadrilateral are
supplementary.
 An exterior angle of a cyclic quadrilateral is equal
to the interior opposite angle.
A  D  1800
C  B  180
0
B
C
D
A
x
BDE  CAB
B
x
D

8. Proving the Cyclic Quadrilateral Theorem- Part 1
The opposite angles of a cyclic quadrilateral
are supplementary.
B
ABD ACD  360
0
Sum of
Arcs
1
C  ABD
2
A
C
Prove that
B  C  180 0.
D
Inscribed
Angle
1
B  ACD
2
Inscribed
Angle
1
1
0
ABD  ACD  180
2
2
Thus,B + C = 180 .
0

9. Proving the Cyclic Quadrilateral Theorem- Part 2
An exterior angle of a cyclic quadrilateral is
equal to the interior opposite angle.
2  4  180
2
3
1
0
Opposite angles of a cyclic
quadrilateral
4  5  180
0
Supplementary Angle Theorem
4
5
4 5  2  4
Transitive Property
Prove that
2 = 5.
Thus,5 = 2.

10. Using the Cyclic Quadrilateral Theorem
1
1030
410
1. _______
490
2. _______
820
3
2
3. _______
280

11. Using the Cyclic Quadrilateral Theorem
800
1. _______
8
6
800
2. _______
350
3. _______
350
4. _______
350
1
4
1000
5
6. _______
1000
7. _______
1000
2
7
1100
5. _______
9
3
8. _______
300
9. _______
300

12. Conclusion
Finally we conclude that this given PPT on Cyclic
Quadrilaterals was very helpful, educational, and was fun
too. So we thank our mathematics teacher for giving us
this PPT assignment. While creating this PPT we had a
great time while doing it and while sharing our ideas.