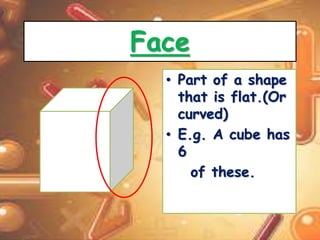
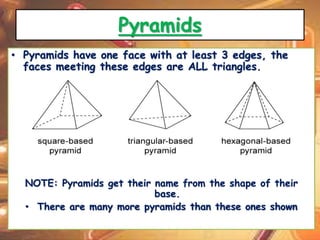
This document discusses different types of 2D and 3D shapes. It describes 2D shapes as flat objects defined by straight or curved lines, including polygons like triangles and squares. 3D shapes have length, width, and height, enclosing a volume. They are characterized by faces, vertices, and edges. The document contrasts 2D and 3D properties, provides examples of 3D shapes like cubes and pyramids, and defines key 3D geometric terms such as faces, edges, and vertices.

1. VISUALIZING SOLID
SHAPES!!!
PRESENTED BY :
SAACHI CHAUHAN

2. CONTENTS…
• WHAT ARE SHAPES?
• 2-DIMENSIONAL SHAPES
• PROPERTIES OF 2-DIMENSIONAL SHAPES
• 3-DIMENSIONAL SHAPES
• PROPERTIES OF 3-DIMENSIONAL SHAPES
• DIFFERENCE BETWEEN 2-DIMENSIONAL AND
3-DIMENSIONAL SHAPES
• FACE’S
• EDGE’S
• VERTICES
• POLYEDRONS , PRISM AND PYRAMIDS

3. WHAT ARE SHAPES?
• A shape is a geometrical figure that
can be described with mathematics.
• For example, two-dimensional shapes
like circles will fit inside of a
flat plane.
• Three-dimensional objects like cubes
will not fit inside of a plane, because
they are not flat.

4. 2-DIMENSIONAL SHAPES
• These are two-dimensional
shapes
or flat
plane geometry
shapes. Their
sides are made of
straight or curved
lines. They can have
any number of sides.
Plane figures made
of lines are called
polygons. Triangles
and squares are
examples of

5. PROPERTIES OF 2-
DIMENSIONAL SHAPES
• Two-dimensional shapes are planar. In the case of a
coordinate system of more than two dimensions, then
a 2-D shape would still depend on two coordinate
directions. For example, in a spatial xyz coordinate
system (which is three-dimensional) a two-dimensional
shape would be expressed with points such as (x,y,0),
(x,0,z), or (0,y,z). Therefore, it would depend on
either x and y, x and z, or y and z.
• 2-D shapes include the square, the triangle, the
rhombus, etc.
• To understand it more easily, you can say that 2-D
shapes do not have prominent or rugged parts. For
example, speaking two-dimensionally you would have a
square, whereas three-dimensionally you would have a

6. 3-DIMENSIONAL SHAPES
• A 3D shape is a solid which encloses a
volume and has length, breadth and
height.

7. 3-DIMENSIONAL SHAPES
SOME MORE 3D SHAPES:
CUBE AND SOME MORE…..

8. PROPERTIES OF 3-
DIMENSIONAL SHAPES
• Three-dimensional shapes have four
properties that set them apart from
two-dimensional shapes: faces,
vertices, edges and volume. These
properties not only allow you to
determine whether the shape is two-or
three-dimensional, but also which
three-dimensional shape it is.

9. DIFFERENCE BETWEEN 2-D
AND 3-D SHAPES
2-DIMENSIONAL
• 2D is 'flat', using
the X & Y
(horizontal and
vertical) axis', the
image has only two
dimensions and if
turned to the side
becomes a line.
3-DIMENSIONAL
• 3D adds the ‘Z’
dimension.
• This third dimension
allows for rotation
and depth.
• It's essentially the
difference between
a painting and a
sculpture.

10. Aq
Platonic
Solid
Picture
Number
of Faces
Shape of
Faces
Number
of Faces
at Each
Vertex
Number
of
Vertices
Number
of Edges
Unfolded
Polyhedron (Net)
Tetrahedron
4
Equilateral
Triangle
(3-sided)
3 4 6
Cube
6
Square
(4-sided)
3 8 12
Octahedron
8
Equilateral
Triangle
(3-sided)
4 6 12
Dodecahedron
12
Regular
Pentagon
(5-sided)
3 20 30
Icosahedron
20
Equilateral
Triangle
(3-sided)
5 12 30

11. Face
• Part of a shape
that is flat.(Or
curved)
• E.g. A cube has
6
of these.

12. Edge
• The line where
two faces meet.
• E.g. A cube has
12 of these.

13. Vertex (Vertices)
• The place where
three or more
edges meet.
• This pyramid
has 4 of these.

14. Polyhedrons
In a convex polyhedron, the line segment joining any two points on
the surface of the polyhedron lies entirely inside or on the
polyhedron.
A polyhedron some of whose plane sections are concave polygons is
known as a concave polyhedron. Concave polygons have at least one
interior angle greater than 180° and has some of its sides bent
inward.
Convex polyhedron

15. Prisms and pyramids
A prism is a polyhedron with parallel congruent polygon bases and
sides made of parallelograms.
A pyramid is a polyhedron whose base is a polygon of any number of
sides and whose lateral faces are triangles with a common vertex.
Prisms and pyramids are named after the shape of their base.
Maps represent the location of a place or object in relation to other
places or objects.
Prisms Pyramids

16. Prisms
• Prisms have two identical, parallel
faces joined to one another by
rectangles. Examples are;

17. Pyramids
• Pyramids have one face with at least 3 edges, the
faces meeting these edges are ALL triangles.
NOTE: Pyramids get their name from the shape of their
base.
• There are many more pyramids than these ones shown