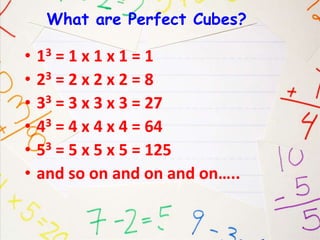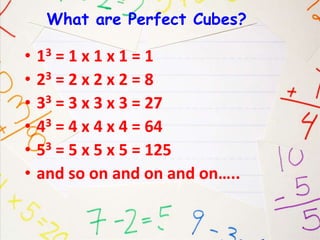
The document discusses cubes and cube roots. A cube is a three-dimensional solid shape where all sides are equal. The cube of a number is when that number is multiplied by itself three times. A perfect cube is a number that can be written as the cube of another number, such as 1, 8, 27, 64, 125 and so on. The cube root of a perfect cube will be an integer, while the cube root of a non-perfect cube may need to be simplified by factoring the number into terms with a cube root of an integer. Examples of simplifying cube roots and finding cube roots of perfect and non-perfect cubes are provided.

1. CH – CUBES AND CUBE ROOT

3. You know that the word
“cube” is used in geometry.
A cube is a solid figure
which has all its sides
equal.

4. Cube Roots
The index of a cube root is
always 3.
Sign of cube root is 3 64

5. What does cube mean?
The cube of a number is…
…the value when multiplied by
itself three times gives the original
number.

6. Perfect Cubes
If a number is a perfect cube, then you can
find its exact cube root.
A perfect cube is a number that can be written
as the cube (raised to third power) of another
number.

7. What are Perfect Cubes?
• 13 = 1 x 1 x 1 = 1
• 23 = 2 x 2 x 2 = 8
• 33 = 3 x 3 x 3 = 27
• 43 = 4 x 4 x 4 = 64
• 53 = 5 x 5 x 5 = 125
• and so on and on and on…..

8. Examples:
3 3 27 
216  63
27 3 3 
216 6 3 

9. Simplify Cube Roots
Not all numbers or expressions have an
exact cube root as in the previous
examples.
If a number is NOT a perfect cube, then you might be
able to SIMPLIFY it.

10. Examples:
perfect cube
  3 27 2 3 2 3
3 10 4 3 6410 
3 3 6 3 3 2 125 4  a a b b 
 3 54 1)
 3 640 2)
3 7 5 500a b 
3 6 3 3 2 125a b  4ab  2 3 2 5a b 4ab